奇特征有限正交空间中全迷向子空间的Critical问题
钱国栋,赵燕冰,霍元极,3
奇特征有限正交空间中全迷向子空间的Critical问题
钱国栋1,赵燕冰2,霍元极1,3
(1.河北北方学院信息与工程学院,河北张家口075000;2.张家口职业技术学院基础部,河北张家口075000; 3.海南软件职业技术学院基础部,海南琼海571000)
利用奇特征正交空间上全迷向子空间的性质及计数定理在奇特征正交空间中研究了全迷向子空间的Critical问题,得到了相应的计数公式和Critical指数.
奇待征正交空间;Critical指数;面;格;matroid;Möbius函数
1 预备知识
设Fq是q个元素的有限域,这里q是一个素数幂,F(n)q是Fq上的n维行向量空间.F(n)q上的经典Critical问题由Crapo和Rota在1970年系统地阐述和研究,给出了Critical指数及其相关的结果(见文献[1]), Kung在文献[2]中研究了辛空间的Critical问题,给出了一些结果,万哲先在有限域上酉空间和辛空间中研究了Critical问题得到一些重要结果(见文献[3]),并纠正了Kung在文献[2]中的一些错误,赵燕冰、钱国栋、霍元极在文献[4]中研究了奇特征有限正交空间中非迷向子空间的Critial问题得到了相应的结果.本文根据文[5,6,7]中的结果,按照文献[3]中的思路,讨论了奇特征有限正交空间中全迷向子空间的Critical问题,也得到了文献[1,3,4,5]中一些相应的结果,解决了文献[5]中遗留的一个问题.
我们沿用文献[5,6]中的名词术语,也用到这两个文献中与此文有关的一些结论,并且用[M1,M2,…, Ml]表示对角分块矩阵,其主对角上依序是方阵M1,M2,…,Ml.
设Fq是一个奇特征的有限域,如1.3节[5],选择一个F*q上确定的非平方元z,令S2ν+δ,Δ是一个Fq上(2ν +δ)×(2ν+δ)非奇对称矩阵其中δ=0,1,2.

由Fq上满足TS2ν+δ,ΔTt=S2ν+δ,Δ的所有(2ν+δ)×(2ν+δ)非奇异矩阵T关于矩阵乘法作成一个群,称该群为Fq上关于S2ν+δ,Δ的2ν+δ阶正交群,表示为O2ν+δ,Δ(Fq,S2ν+δ,Δ).
群O2ν+σ,Δ(Fq,S2ν+δ,Δ)在2ν+σ维向量空间F2ν+δq上的作用定义如下
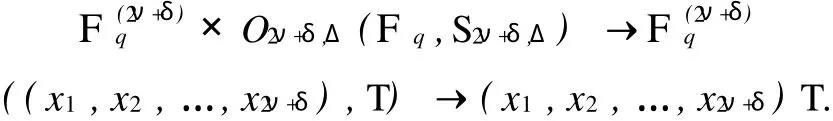
向量空间F(2ν+δ)q与如上O2ν+δ,Δ(Fq,S2ν+δ,Δ)的群作用一起被叫做奇特征有域Fq上2ν+δ维正交空间.设P是 F2qν+δ的m维子空间,由定理1.26[5],PS2ν+δP′合同于
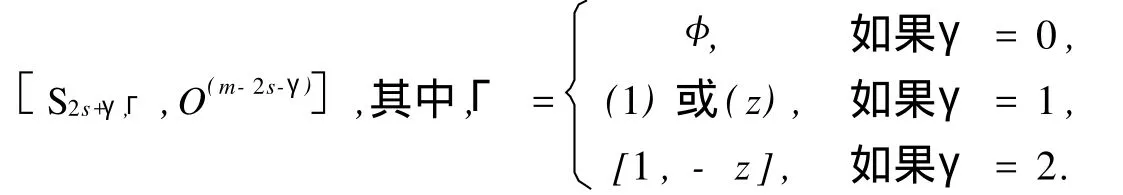
我们称如上的P是(m,2s+γ,s,Γ)型子空间.如果2s+γ=0,就称(m,2s+γ,s,Γ)型子空间为全迷向子空间;或者,一个子空间P是全迷向的当且仅当PSP′=0,如果P是F(2ν+δ)q的一个m维子空间,秩为m的m×(2ν +δ)矩阵也用P表示,它的行向量扩张为一个子空间P,并且叫这个矩阵P为这个子空间P的矩阵表示.
引理1[5]用(m,2s+γ,s,Γ)⊥表示(m,2s+γ,s,Γ)型子空间在F(2ν+δ)q中关于S2ν+δ,Δ的对偶空间,(m,2s +γ,s,Γ)满足
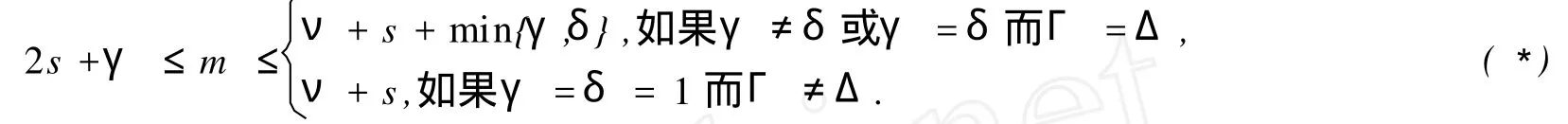
那么(m,2s+γ,Γ)⊥为
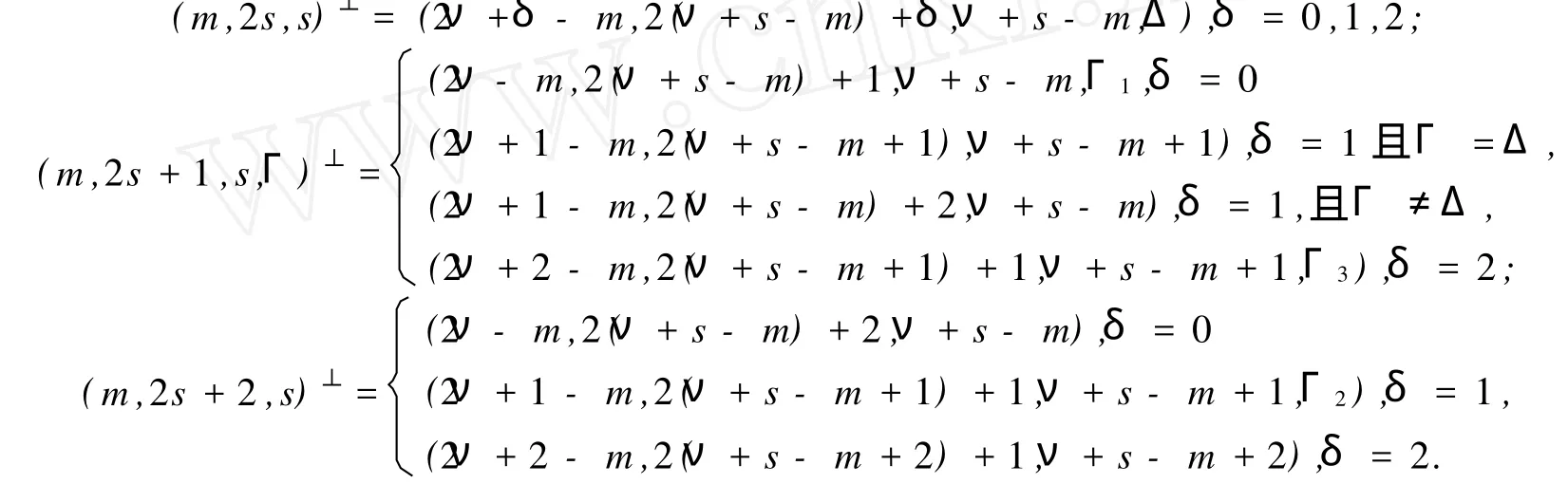
其中,

引理2 设0≤r≤m,在2ν+δ维正交空间犉2ν+δq上包含一个给定r维全迷向子空间的m维全迷向子空间的个数是
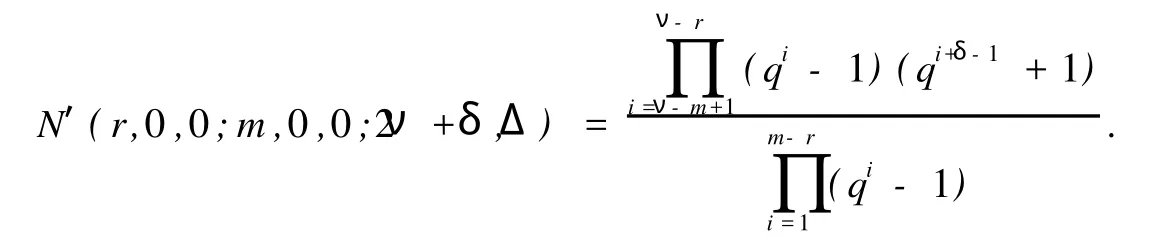
证明 当r=0时,引理2由推论6.23[5]直接可得.
现在假设r>0,由定理6.43[5]及引理1包含一个给定的r维全迷向子空间的m维全迷向子空间的m维全迷向子空间的个数是
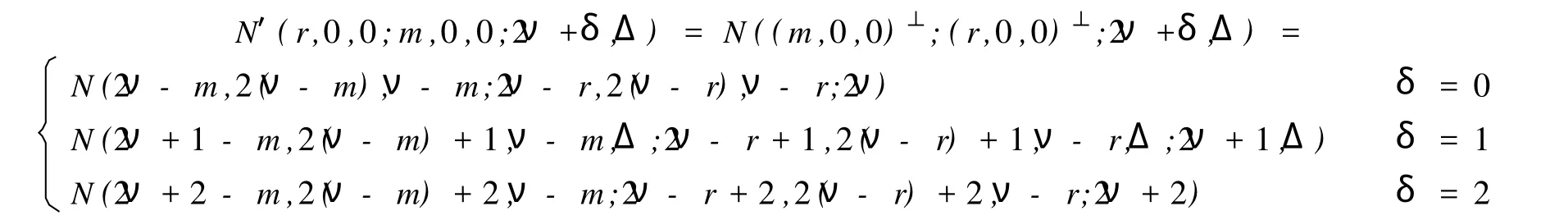
由定理6.33[5]
(1)δ=0时,k满足min{r,m}≥k≥max{0,r}.由于0 (2)δ=1时,k满足min{r,m}≥k≥max{0,r}.由于0 N′(r,0,0;m,0,0;2ν+δ,Δ)=N(2ν+1-m,2(ν-m)+1,ν-m,Δ;2ν-r+1,2(ν-r)+1,ν-r,Δ;2ν+1,Δ) (3)δ=2时,k满足min{r,m}≥k≥max{0,r}.由于0 所以 奇特征正交空间F(2ν+δ)q上向量集X叫做一个迷向集,如果uSν′=0,对于所有的u,v∈X.用〈X〉表示由 X扩张成的子空间.显然,如果X是一个向量的迷向集,则〈X〉是一个全迷向子空间.向量集X的秩定义为〈X〉的维数,用r(X)表示,当X=φ,那么,〈X〉=φ且r(X)=0. 令S是奇特征正交空间F(2ν+δ)q上一个非零向量集,一个全迷向子空间P被叫做是分离S的,如果P∩S =φ.S的正交Critical指数被定义为存在一个最小正整数λ≤ν+1,使得存在一个(ν+1-λ)维全迷向子空间分离S,表示为Corth(S,F2ν+δq).令P1,P2,…,Pλ是λ个极大全迷向子空间,(P1,P2,…,Pλ)叫做极大全迷向子空间的λ元组,如果dim(P1∩P2)=ν-1,dim(P1∩P1∩P3)=ν-2,…,dim(P1∩P1∩P3∩…∩Pλ)=ν+ 1-λ. 因为任何(ν+1-λ)维全迷向子空间是极大全迷向子空间的一个λ元组的交,这个S的正交Citical指数也可定义为ν维极大全迷向子空间Pi(i=1,2,…,λ)所成的λ元组(P1,P2,…,Pλ)与S分离,即(∩λi=1Pi)∩S =φ,这些λ元组中,最小的λ成为S的正交Critical指数.按照惯例,我们也认为0元组的全迷向子空间的交 是F(2ν+δ)q. 令S是一个正交空间F2ν+δq中非零向量的集合,M(S)是被线性无关向量定义的S上的matriod,L(M (S))是M(S)的面格,一个迷向面也是一个向量迷向集,显然,向量迷向集的子集也是迷向的.迷向面的集族在格L(M(S))中形成一个理想并且这个理想用LI(M(S))表示. 引理3 设0≤r≤m,在2ν+δ维正交空间F2ν+δq上包含一个给定秩为r的迷向集的m维全迷向子空间的个数是 证明 当r=r(X)=0时,引理3由推论6.23[5]直接可得. 现在假设r>0,令P是一个m维全迷向子空间,那P⊃X当且仅当P⊃〈X〉,因此,由引理2得证.推论4 在2ν+δ维正交空间F2ν+δq上包含一个给定秩r的迷向集的极大全迷向子空间的个数是 定理5 设S是2ν+δ维正交空间F(2ν+δ)q中的(m,2s+γ,s,Γ)型非零向量的集合,(m,2s+γ,s,Γ)满足(*),M(S)是被线性无关向量定义的matroid,L(M(S))是M(S)的面格,LI(M(S))是在格L(M(S))中迷向面的理想,μ是L(M(S))上的Möbius函数那么,对任保正整数λ≤ν+1,分离S的ν+1-λ维全迷向子空间的个数是 证明 因为ν+1-λ维全迷向子空间为(ν+1-λ,0,0)型,所以(ν+1-λ,0,0)满足(*).设X是M(S)的一个面,用g(λ,X)表示包含X的ν+1-λ维全迷向子空间的个数,所以由引理2得 用f(λ,X)表示使得P∩S=X的ν+1-λ维全迷向子空间P的个数,那么, 由Möbius反演公式得, 对于Y=φ,f(λ,φ)是分离S的ν+1-λ维全迷向子空间的个数 其中m1=r(X)≤ν+1-λ. 推论6 设S是2ν+δ维正交空间F(2ν+δ)q中非零向量的集合,M(S),L(M(S)),LIM(S),μ,与定理5相同,其中m1=r(X)≤ν+1-ε.那么 定理7 设S是2ν+δ维正交空间F(2ν+δ)q中非零向量的集合,那么极大全迷向子空间的λ元组与S分离的个数为 证明 依据推论4应用定理5类似的方法可证该定理. 推论8 设S是2ν+δ维正交空间F(2ν+δ)q中非零向量的集合,那么 [1] CRAPO H H,ROTA G C.On the Foundations of Combinatorial Theory:Combinatorial Geometries[M].Preliminary Edition,M I T Press,Cambridge,1970. [2] KUNGJ P S.Pfaffian Structures and Critical Problem in Finite Symplectic Spaces[J].A nnals of Combinatorics,1997, 159172. [3] WAN Z X.Critical Problem in Finite Vector Spaces[J].Codes and Designs,2002,10:293-303. [4] 赵燕冰,钱国栋,霍元极.奇特征有限正交空间中非迷向子空间的Critical问题[J].应用数学学报,2009,32(5):858-873. [5] WAN Z X.Geometry of Classical Groups Over Finite(Second Edition)[M].Beijing:Science Press,2002. [6] MARTIN A.Combinatorial Theory[M].New York Berlin,Heidelberg:Springer-Verlag,1979. [7] WELSH D J A.Matroid Theory[M].London,New York:Academi Press,1976. Critical Problems of Totally Isotropic Subspaces in Finite Orthogonal Spaces of Odd Characteristic QIAN Guo-dong1,ZHAO Yan-bing2,HUO Yuan-ji1,3 With the properties and counting theorems of the finite orthogonal spaces of odd characteristic, the critical problems of totally isotropic subspaces in the finite orthogonal spaces of odd characteristic was studied and the corresponding counting formulas and critical exponents was obtanied. orthogonal spaces over finite fields of odd characteristic;critical exponent;flat;lattice;matroid; Möbius function O152.8 A 0253-2395(2010)03-0366-05 2009-11-09; 2010-03-23 海南省自然科学基金(109006) 钱国栋(1964-),男,河北万全人,学士,讲师,研究领域为计算机与编码理论.E-mail:zjkzyb@tom.com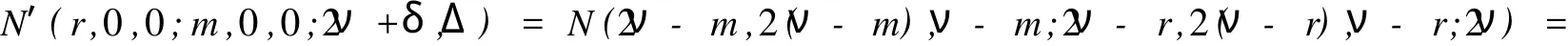
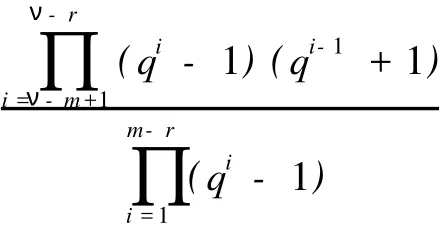
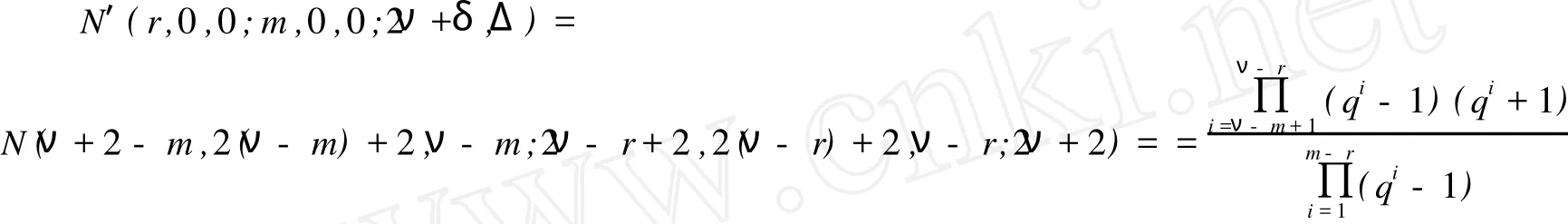

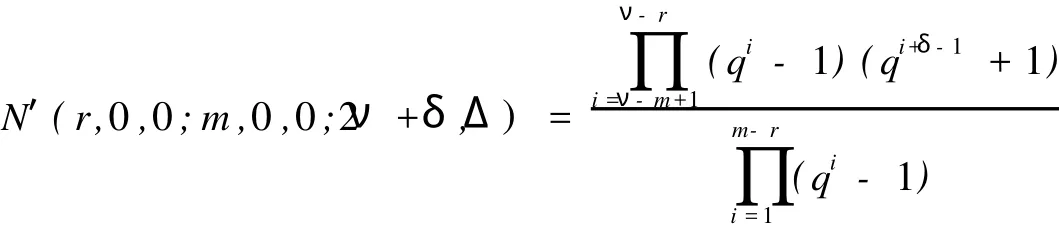
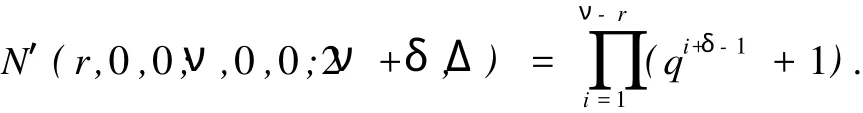
2 主要结论
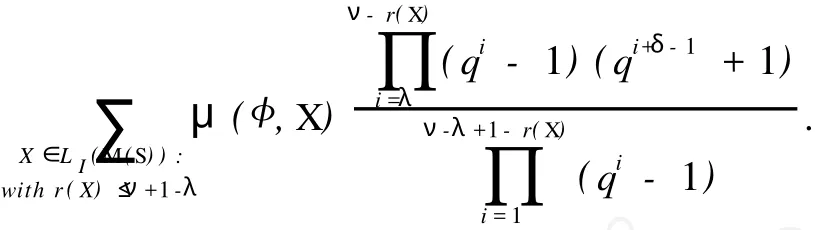
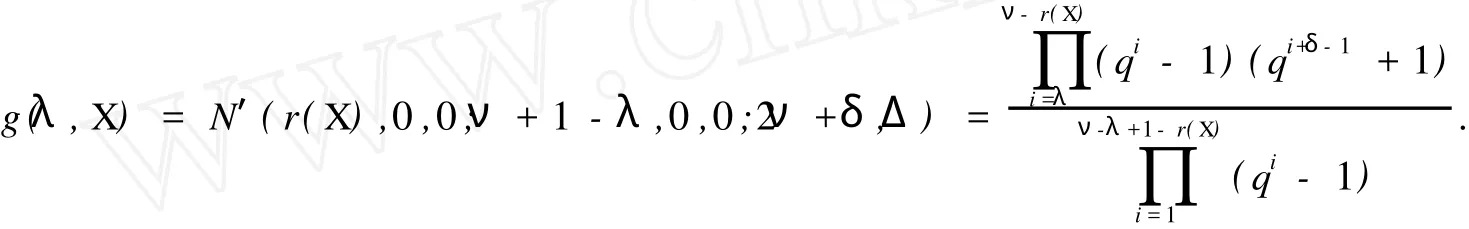
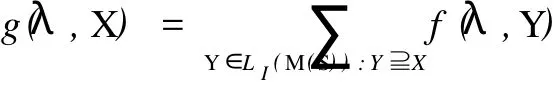
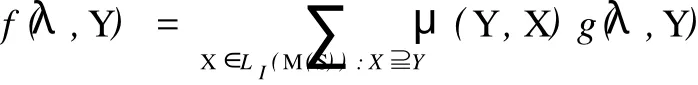
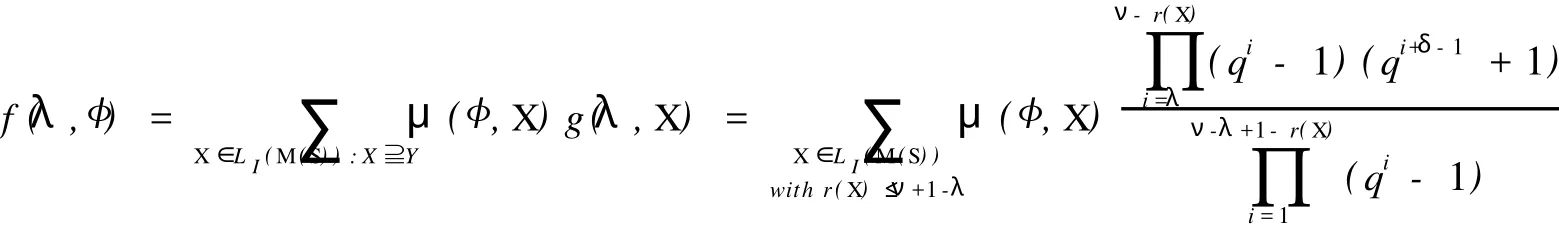
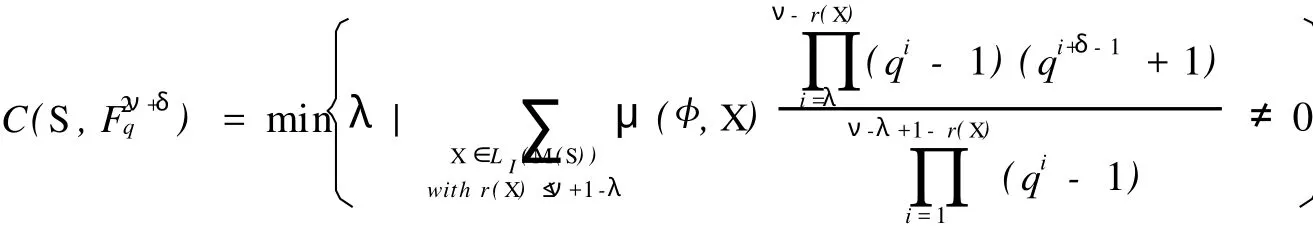
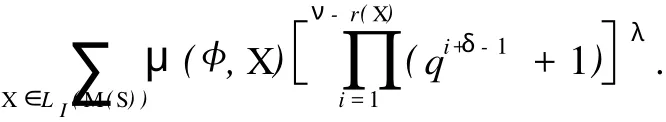

(1.College of Inf ormation Engineering,Hebei North University,Zhangjiakou075000,China; 2.Department of Basic Coures,Zhangjiakou Vocational College ofTechnology,Zhanjiakou075000,China; 3.Department of Basic Courses,Hainan Sof tware Prof ession Institute,Qionghai571000,China)

