一类极小谱任意符号模式矩阵

高 玮,洪世煌

(杭州电子科技大学理学院,浙江杭州310018)

0 引 言

符号模式矩阵是指元素取自集合{+,-,0}的矩阵,简称符号模式。对于给定实矩阵B=(bij),由bij的符号为元素所组成的矩阵称为B的符号模式,记为sgn B。用Qn表示全体n阶符号模式组成的集合。对任意A∈Qn,所有与A有相同符号模式的实矩阵组成的集合{B|sgn B=A}称为A所决定的定性矩阵类,记为Q(A)。一个实矩阵B是幂零的是指对某个正整数k,有Bk=0,即B的特征多项式为g(x)=xn。若存在实矩阵B∈Q(A)是幂零的,则称符号模式A蕴含幂零。将符号模式A中的某些非零元用零代替后得到的符号模式称为A的子模式,也称A为的母模式。每个符号模式都是其自身的母模式和子模式。如果对任意一个n次首项系数为1的实系数多项式g(x),在n阶符号模式A的定性矩阵类Q(A)中至少存在一个实矩阵B,使得B的特征多项式为g(x),则称A为谱任意符号模式。如果一个谱任意符号模式的任意非零元被零取代后所得到的符号模式不是谱任意的,则称该谱任意符号模式为极小谱任意符号模式。谱任意符号模式一定是蕴含幂零的。研究谱任意符号模式矩阵的问题最早出现在文献1中,该文基于隐函数存在定理,给出了证明一个符号模式和它的所有母模式都是谱任意的方法(见下面引理1)。文献2给出了第一个n≥2阶谱任意符号模式,文献3-5等分别给出了一些谱任意符号模式。目前,寻找非零元个数最小的谱任意符号模式仍然是符号模式矩阵研究中一个重要的问题。本文运用幂零—雅可比方法给出了一类n≥4阶极小谱任意符号模式矩阵。

1 幂零—雅可比方法

设x1,…,xn是n个变量,fi是关于x1,…,xn的函数(i=1,2,…,n),且对于所有的i,j∈{1,…,n},都存在。雅可比行列式是一个n阶行列式,它的(i,j)元素为(1≤i,j≤n)。

引理1 设A是阶符号模式,存在B=(bij)∈Q(A)为幂零矩阵,且B中至少有n个非零元,记为…,binjn。用变量x1,…,xn,替换B中这n个非零元得到的矩阵记为X,并设X的特征多项式为gx(x)=det(xI-X)=xn+f1xn-1+…+fn-1x+fn。若雅可比行列式在幂零点(x1,…,xn)=(bi1j1,…,binjn)处不等于零,则A的任意母模式都是谱任意的[1,3]。

上述引理所给出的方法称为幂零—雅可比方法。

2 主要结果

本文讨论下面一n类阶符号模式矩阵A(其中n≥4且1≤k≤n-3):

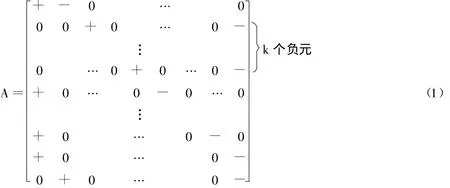
取实矩阵B∈Q(A)有如下形式(其中ai＞0,i=1,2,…,n):

引理2 设 gB(x)=det(xI-B)=xn+f1xn-1+…+fn-1x+fn,则:

(1)f1=1-a1,

f2=a2an-a1,

fi=aian-a1ai-1an,i=3,4,…,k+1(k≥2),

fk+2=ak+2-a1ak+1an(k≤n-4),

fi=(-1)k+i+2(ai-ai-1),i=k+3,k+4,…,n-2(k≤n-5),

f n-1=(-1)n+k(an-2-an-1-an)(如果k=n-3,f n-1=-a1 an-2 an+an-1+an),

fn=(-1)n+k+1(an-1-a1an);

证明 (1)将行列式det(xI-B)按最后一行展开,得:

经整理得(1)成立。

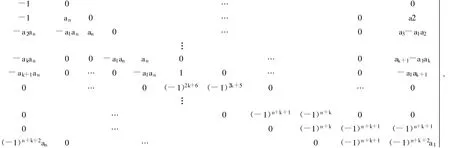
将上式按第一行展开,然后依次将第i行的a1倍加到第i+1行,i=1,2,…,k,再分别按第1,2,…,k列展开,得当k=n-3时,类似可得

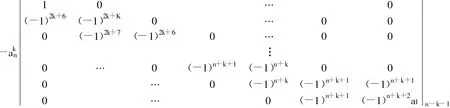
引理得证。

定理1 对于n≥4且1≤k≤n-3,A的所有母模式都是谱任意的。

证明 当b1=1,b2=…=bk+1=2,bk+2=…=时,由引理2(1)可知,B为幂零矩阵,故符号模式矩阵A蕴含幂零,再由引理2(2),(a1+1)≠0。因此,引理1说明了A的所有母模式都是谱任意的。

定理得证。

定理2 对于n≥4且1≤k≤n-3,A为极小谱任意符号模式矩阵。

证明 设S=(si,j)是A的一个子模式,且为谱任意的。

(1)s1,1≠0,sn,n≠0。否则Q(S)中所有矩阵的迹恒为负或恒为正,与S为谱任意相矛盾。

(2)s1,1≠0,否则Q(S)中所有矩阵均为非奇异矩阵,与为谱任意相矛盾。

(3)si,i+1≠0(i=2,…,n-1),否则Q(S)中所有矩阵均为奇异矩阵,也S与为谱任意矛盾。

(4)因为S是谱任意的,则必存在B∈Q(S)是幂零矩阵。因对任意常数c＞0,cB∈Q(S)且cB也是幂零矩阵,又相似矩阵有相同的特征多项式,故不妨设B有形式(2)。由引理2(1)中的f1=f2=…=fn=0可知ai≠0(i=1,2,…,n),从而 si,n≠0(i=1,2,…,k+1),si,1≠0(i=k+2,…,n-1),sn,2≠0。

综合上述讨论知S=A,即A为极小谱任意符号模式矩阵。

定理得证。

[1] Drew JH,JohnsonC R,Olesky DD,et al.Spectrally arbitrary patterns[J].Linear Algebra and its Applications,2000,(1):121-137.

[2] McDonald JJ,Olesky D D,Tsatsomeros M J,et al.On the spectra of striped sign patterns[J].Linear and Mu ltilinear Algebra,2003,51(1):39-48.

[3] Britz T,M cDonald JJ,Olesky D D,et al.Minimal spectrally arbitrary sign patterns[J].SIAM Journal on Matrix Analysis and Applications,2004,26(1):257-271.

[4] LiShoucang,Gao Yubin.Two new classes of spectrally arbitrary sign patterns[J].Ars Combinatoria,2009,90(1):209-220.

[5] 李茜,邵燕灵,高玉斌.A new class of minimally spectrally arbitrary sign patterns[J].数学研究与评论,2008,28(2):389-395.