Ginzburg-Landau方程的随机摄动

包立平,郑 薇

(杭州电子科技大学理学院,浙江杭州310018)

0 引 言

具有白噪声干扰的金茨堡-朗道方程问题,是十分有意义的问题。其在物理学和统计力学方面有着广泛的应用,尤其在超导理论方面有着重要的作用,因而引起了人们的广泛关注[1-3]。到目前为止,对于一维的金茨堡-朗道方程的随机摄动问题的研究相对比较深入,国外的大量文献用数值解的方法和几何流形,测度论方面研究了金茨堡-朗道方程的随机摄动问题及该方程自被控项链环孤立子和三维高次的稳定耗散光学孤立子问题[2-5];国内的文献主要研究了该方程的格子玻尔兹曼数值解[1,6]。对于二维的金茨堡-朗道方程的随机摄动问题的研究相对较少。本文主要研究平面上具白噪声干扰的金茨堡-朗道方程的随机摄动问题并将其结果推广到了n维空间。通过构造适当的格林函数,给出了该方程解的随机微分表达式,得到了其形式渐近展开式,并分析了该方程解的期望与方差,从而在方差的意义下,得到了解的余项估计。

1 解的渐近展开

本文讨论如下的具有白噪声干扰的Ginzburg-Landau方程问题:

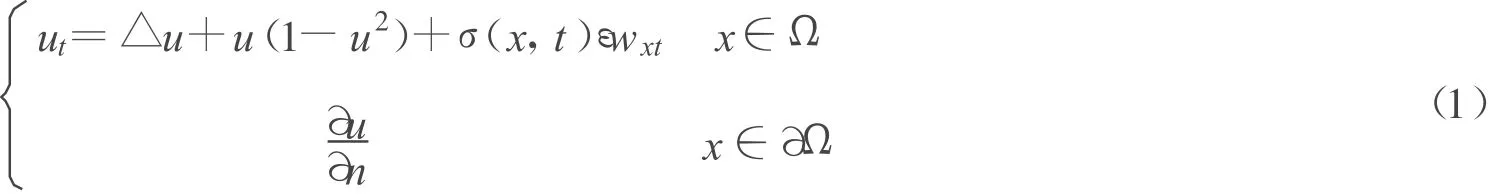
式中,Ω=BR(0)⊂R2,σ(x,t)∈C(R2),u为实函数 t＞0,u0(x,0)=1,{W(x,t)}是标准两参数Wiener过 ,且 W(x,t)=Ωw(y,s)dyds,这里w是高斯白噪声,Ew(y,t)=0,且 E[w(x,t)w(y,s)]=δ(x-y)δ(t-s)。

设:

先作形式渐近展开,其首项满足如下问题:

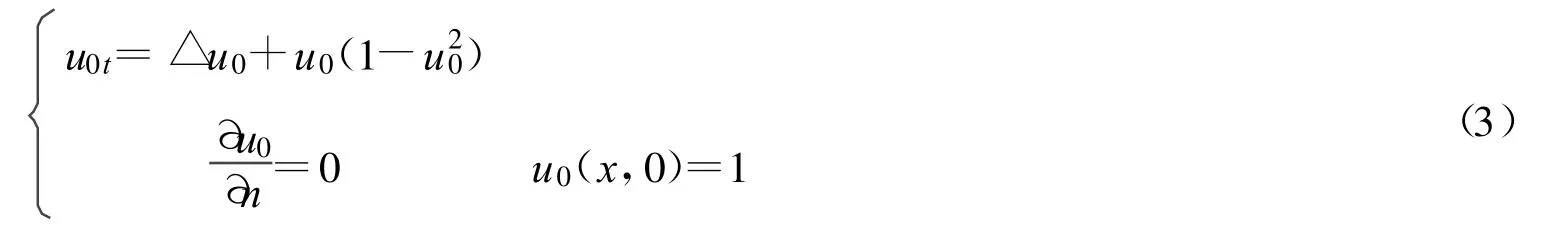
引理1 式3的解 u0=1。

证1,▽u0=0。由式4可知,Ω(u0t)2dx=0,所以 u0t=0,即 u0为常数。又因为 u0(x,0)=1,所以 u0=1,证毕。

由式2可得,其 u1,uk(k≥2)满足如下问题:

因此:

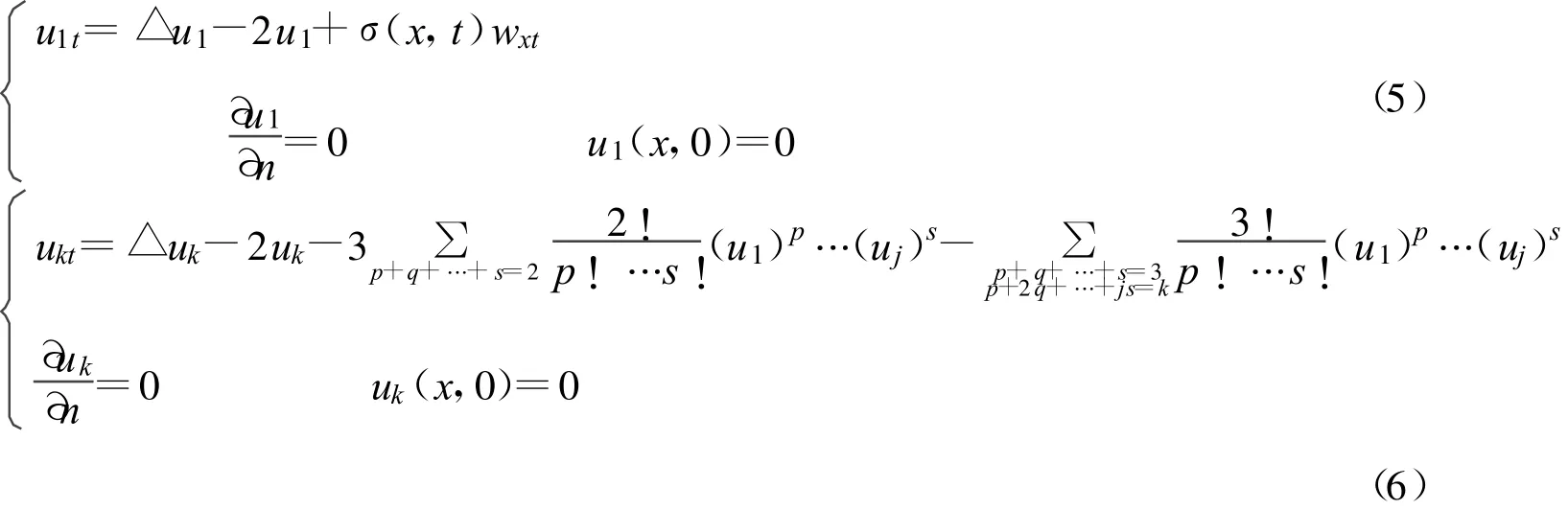
2 Green函数

在讨论式1的期望与方差分析前,考虑如下的问题:

令x1=rcosθ,x2=rsinθ,0≤r≤R,0≤θ≤2π,则可得 :

利用分离变量法可得其格林函数为:

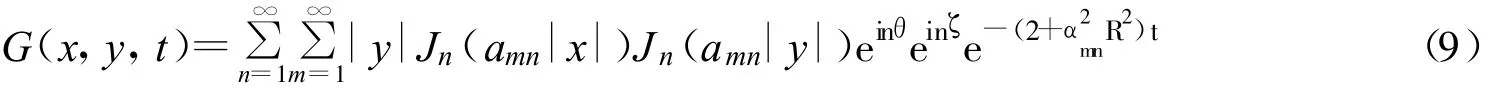
式中,Jn(x)为Bessel函数,αmnR是 Jn(x)的零点

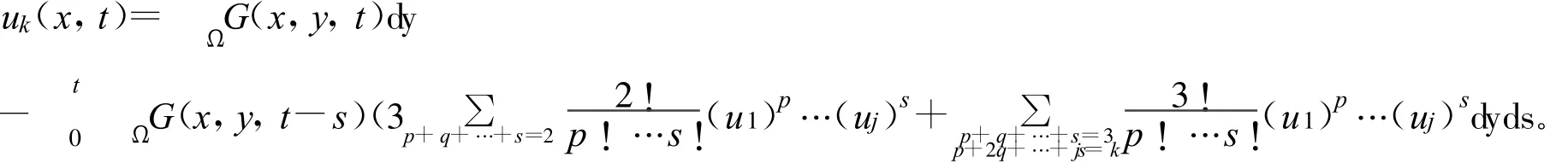
证 由式5知:

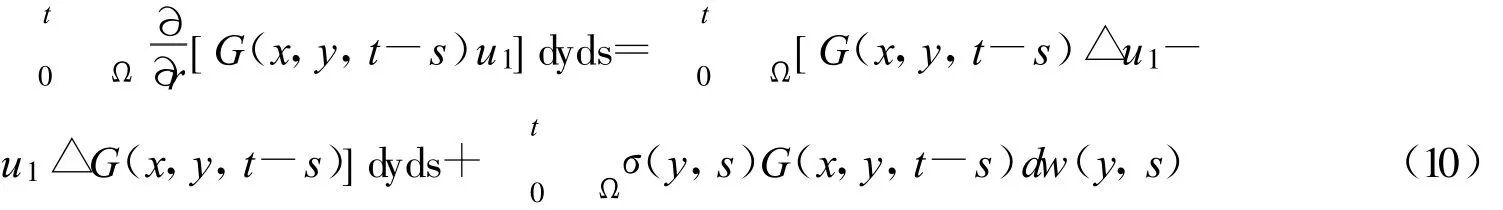
同理由式6可得:

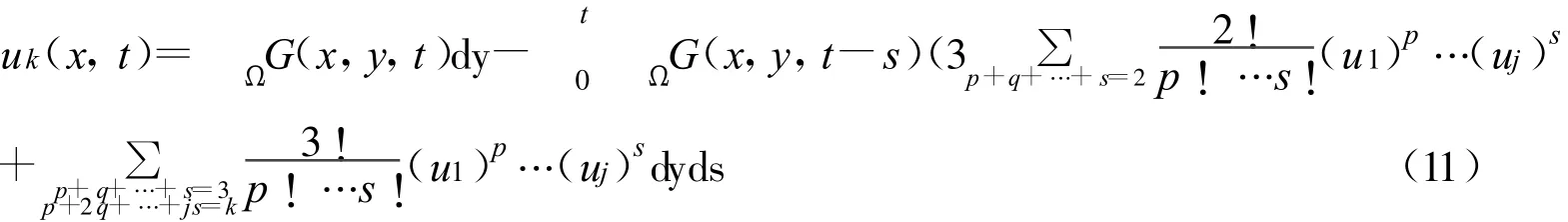
证毕。

3 期望、方差与余项估计

定理1 式1的解 u=1+εu1+ε2u2+…εkuk+εk+1R,|E R|≤c,|V ar R|≤c这里c是与ε无关的常数。

证 由引理2可知E u1=ΩG(x,y,t)dy,由 Ito积分可得Var u1=dyds,由渐近展开式 u=1+εu1+ε2u2+…εkuk+εk+1R代入式1得:

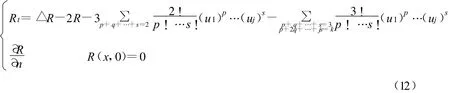
因此:

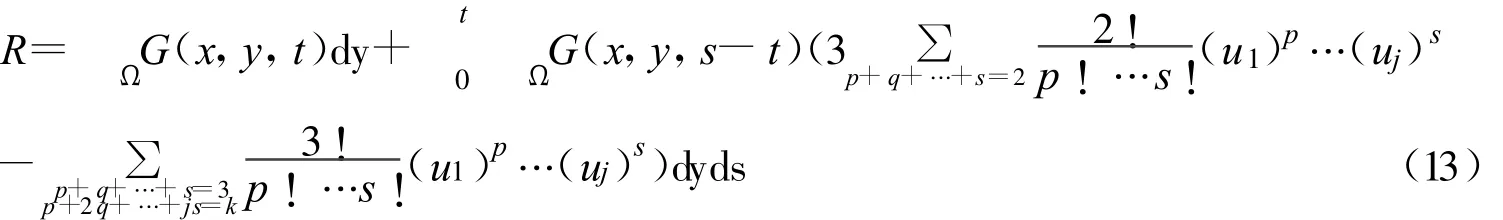
则ER=ΩG(x,y,t)dy-

由递推可得:|E R|≤c,

因此可得:|Var R|≤c,即在方差意义下:

证毕。

[1] Yang Desheng.The asymptotic behavior of the stochastic Ginzburg Landau equation with multiplicative noise[J].Mathemtical Physics,2004,45(11):4 065-4 076.

[2] He Y J,Fan H H,Dong JW,et al.Self-trapped spatiotemporal necklace-ring solitons in the Ginzburg-Landau equation[J].Physical Review,2006,74(1):1 661-1 665.

[3] Mihalache D,Mazilu D,Lederer F,et al.Stability of dissipativeoptical solitons in the three-dimensional cubic-quintic Ginzburg-Landau equation[J].Physical Review,2007,75(3):33 811-33 818.

[4] Hakima,Bessaih.Semi-linearized compressible Navier-Stokes equation perturbed by noise[J].Electronic Journalof Differential Equations,2003,3(2):1-18.

[5] Nils Berglund,BarbaraGentz.Geometric singular perturbation theory for stochastic differential equations[J].Differential Equations,2003,(1):1-54.

[6] 闫广武,闫冰.Ginzburg-Landau方程的格子Boltzman解[J].非线性动力学学报,2002,9(3):154-158.