波谱单元法在空间桁架地震响应分析中的应用

张俊兵，朱宏平，王丹生，閤东东

(1.华中科技大学 土木工程与力学学院，武汉 430074;2.华中科技大学 控制结构湖北省重点实验室，武汉 430074)

波谱单元法在空间桁架地震响应分析中的应用

张俊兵1，2，朱宏平1，2，王丹生1，2，閤东东1，2

(1.华中科技大学 土木工程与力学学院，武汉 430074;2.华中科技大学 控制结构湖北省重点实验室，武汉 430074)

针对传统波谱单元法(SEM)只能用于求解节点集中荷载作用下结构动力响应问题的不足，提出了一种通过计算地震等效波谱节点荷载求解桁架结构地震响应的方法。基于虚功原理，利用波谱形函数积分得到地震等效波谱节点荷载的显式表达式，通过修改波谱单元法中单元刚度矩阵的波数，考虑了阻尼对结构动力特征的影响，采用数值拉普拉斯(Laplace)变换替换快速傅里叶(FFT)变换，回避了传统波谱单元法中FFT的周期性问题。利用地震荷载等效后的波谱节点荷载对三维空间桁架结构进行地震响应分析，结果表明，采用本文的方法能方便的计算桁架结构的地震等效波谱节点荷载，精确求解结构的地震响应，与传统有限元法(FEM)相比，大大减少计算单元数量，提高计算精度，且便于编程计算。

波谱单元法;阻尼;波数;桁架;有限元;地震响应

计算机技术的发展使得有限元法在各类工程问题中得到广泛应用。为满足工程计算精度，采用有限元法对实际结构进行分析时需要大量划分单元，从而导致计算量大大增加［1］。相比于传统的有限元法，基于连续质量体系动力分析的波谱单元法，对连续均匀的构件进行分析，不论构件长度如何，在构件的连续均匀部分只需要一个单元［2］。该方法利用连续质量体系平衡微分方程的精确波动解作为形函数，形成与频率相关的动态刚度矩阵并进行求解，因而能够精确描述结构的动力特征［3］，在不增加单元数量的情况下大大提高计算精度。Doyle［2，4，5］和 Lee［1，6］等采用基于快速傅里叶变换(FFT)的波谱单元法对集中动荷载作用下的杆件、梁和板进行分析，成功求得结构的动力响应。由于FFT具有周期性，利用基于FFT变换的波谱单元法进行结构动力响应分析时，必须在波谱分析中考虑无限长单元［4］(throw-off element)。然而，无限长单元在计算时会将系统能量导出［4］，从而导致计算误差。日本学者Igawa和Komatsu等［7］利用数值Laplace变换代替FFT变换，求解有限长系统，取得了很好的效果。传统的波谱单元法只能对集中荷载作用下的结构进行分析，Lee等［8］利用线性叠加原理得到了分布荷载作用下梁的动力响应，但该文的方法计算分布荷载时采用数值积分，不但计算误差大，而且针对不同的结构需要采用不同的积分表达式，因而不适合大型结构的编程计算。结构阻尼是结构的固有特性，直接影响到结构的动力特征，但到目前为止，大多数学者［1－9］利用波谱单元法进行动力分析时仍未考虑阻尼的影响。

本文采用基于Laplace变换的波谱单元法对桁架结构进行分析，回避了传统波谱单元法中FFT变换的周期性问题。基于虚功原理，通过对形函数进行积分计算，推导了地震荷载作用下桁架结构的地震等效波谱节点荷载的显式表达式，通过修改波谱单元刚度矩阵的波数，考虑了结构阻尼的影响。利用等效后的地震波谱节点荷载对钢桁架桥具有200根杆的空间桁架进行地震响应分析，数值算例结果表明，采用本文的方法的能十分方便的进行编程计算，修正后的波谱单元法能有效求解桁架结构的地震响应，减少计算单元数，提高计算精度。

1 杆的平衡微分方程

考虑如图1所示均匀线弹性杆受到轴向力作用及地震产生的支座激励，根据微段受力平衡可得［10］

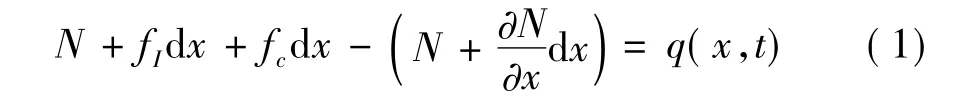
式中N=N(x，t)表示杆件轴向力，可以写为:

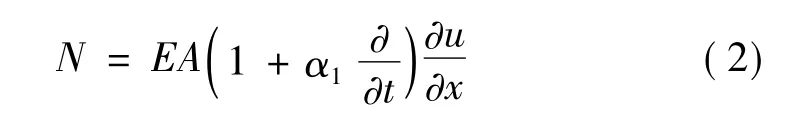
式中:u=u(x，t)为杆件相对于单元坐标的轴向位移;E为弹性模量;A为杆件截面面积;α1为杆件内部粘弹性阻尼系数;q(x，t)为沿杆件长度方向作用的外荷载，若杆件仅受地震作用，则外荷载q(x，t)=0。

式中fI和fc分别为单位长度的惯性力和粘滞阻尼力。分别写为:

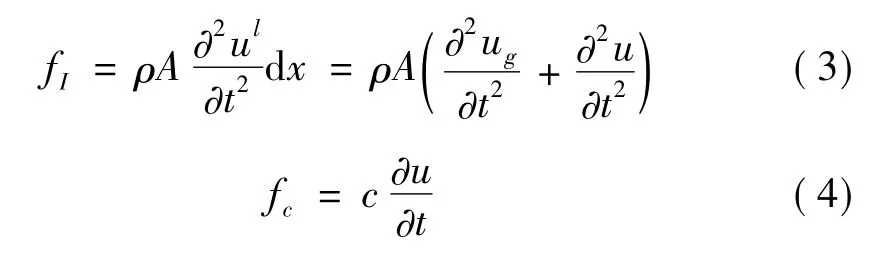
其中:ρA为单位长度质量;ut=ut(x，t)为杆件相对于固定参考轴的轴向位移;ug=ug(x，t)为地震作用产生的支座位移;c为与速度相关的外部粘滞阻尼系数。

将式(2)－式(4)代入式(1)中并化简，得到地震作用下杆的平衡微分方程为［10］:

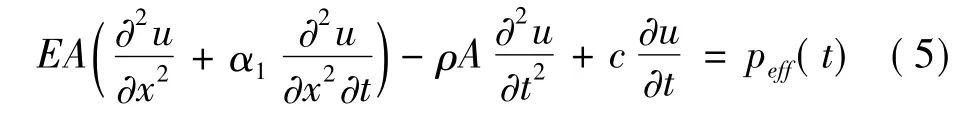
式中peff(t)为地震等效支座激励荷载，写为:

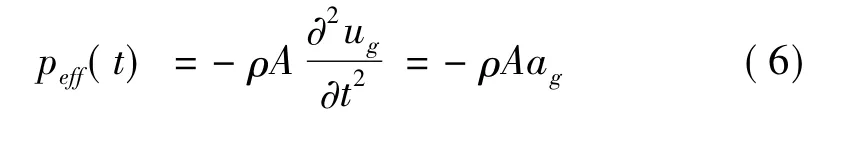
式中ag为地面加速度。

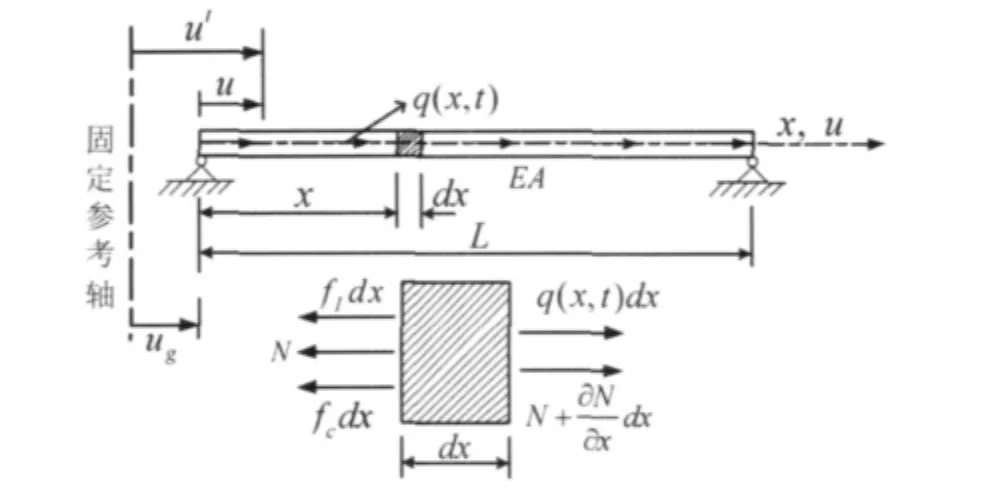
图1 支座激励下杆受力平衡计算简图Fig.1 Model of bar subjected to support excitation

2 杆的波谱单元刚度矩阵

将式(5)两边进行数值Laplace变换，并考虑杆件端部的边界条件，则频域内杆的平衡微分方程可以简写为:

式中:U=U(x，w)为杆件在频域内的轴向位移表达式;s为Laplace变换参数;Peff=Peff(x，w)为频域内的支座激励荷载;x为节点坐标位置函数，如图2所示;符号(″)表示对x求二阶偏导。

图2 杆的波谱节点荷载和位移Fig.2 Spectral nodal forces and displacements

为得到杆件自由振动下的波谱关系，假定式(7)右侧的支座激励荷载Peff=0。此时式(7)写为:

式中kr为波数，写成:

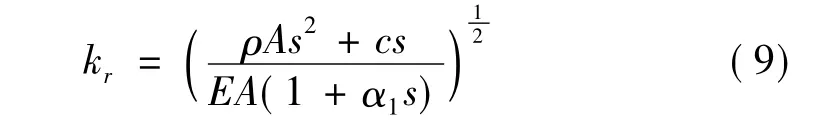
式中的波数包含了阻尼项，在既有波谱单元法的基础上考虑了结构阻尼。

式(8)的解可以表示为:

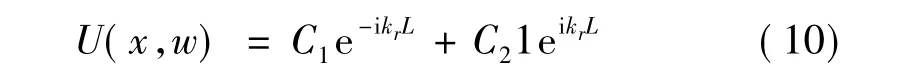
考虑相应的位移边界条件:

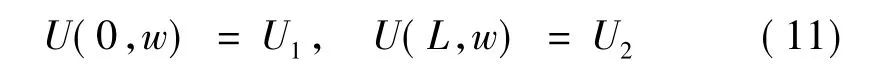
将式(11)中的位移边界条件代入式(10)，则式(8)的解可以用单元的节点位移表示为:

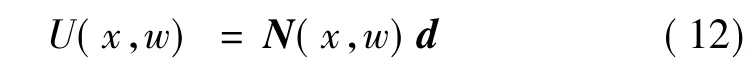
式中d为节点位移向量，表示为:

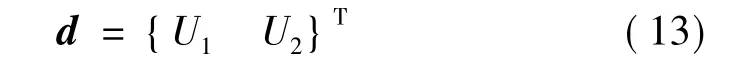
式中N(x，w)为与频率相关的形函数，表示为:

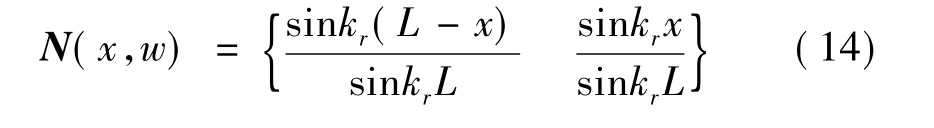
用虚功原理表示式(7)，可以写为:

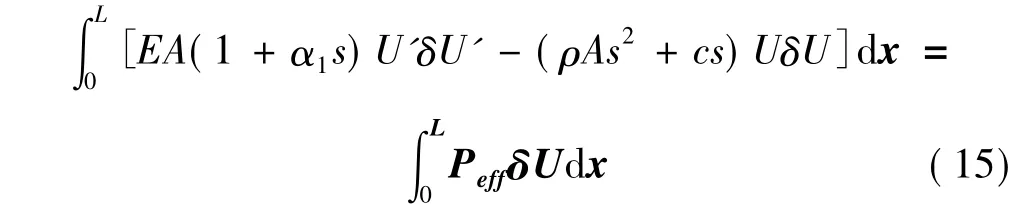
式中符号(')表示对x求偏导，δ为变分符号。

将式(12)代入式(15)，则杆的平衡微分方程可以表示为向量形式［10］

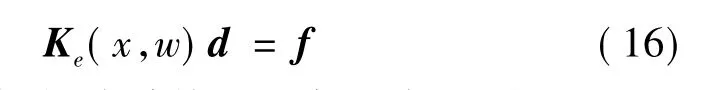
式中:Ke(x，w)为杆的波谱单元刚度矩阵，写为:

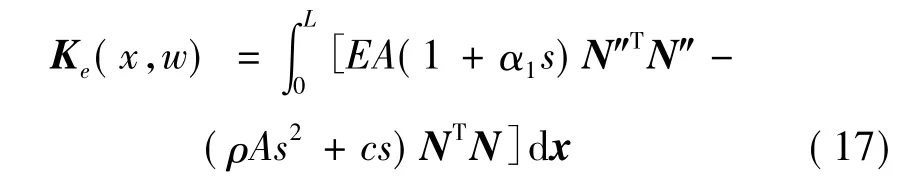
式中f为波谱等效节点荷载向量，写为:

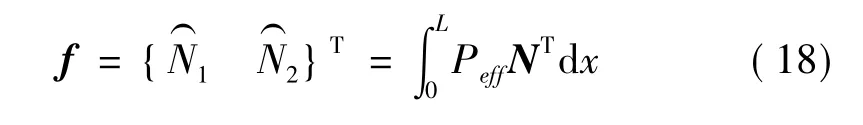
将式(14)中的形函数N(x，w)代入式(17)，把杆的波谱单元刚度矩阵Ke(x，w)写成矩阵形式［1，6，7］:

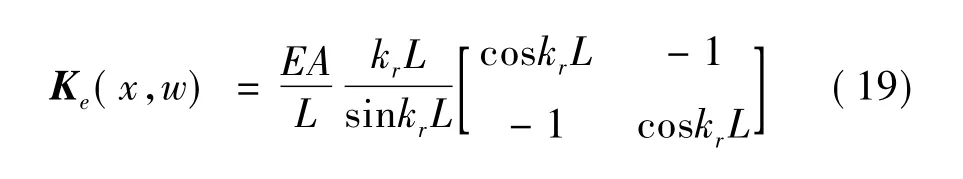
3 地震等效波谱节点荷载

3.1 承受均布荷载杆的等效波谱节点荷载

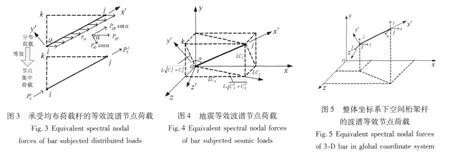
假设均匀线弹性杆受与沿杆轴向成α角的均布荷载 Peff(x，t)作用，通过 Laplace 变换，Peff(x，t)在频域内表示为Peff(x，w)，考虑其均匀分布，将 Peff(x，w)简写为Peff。如图3所示，将Peff分解为沿杆轴向的分量P∥=Peffsinα和垂直于杆轴向的分量P⊥=－Peffcosα。考虑到杆只能承受轴向力，联立式(14)和式(18)，即可得到杆的等效波谱节点荷载为:

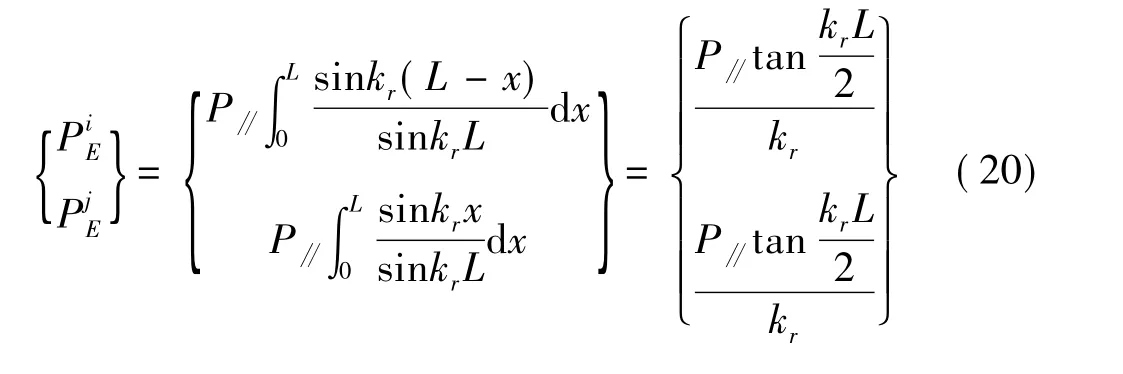
3.2 空间桁架杆的地震等效波谱节点荷载

考虑图4所示的空间桁架杆受到水平地震作用。图中x－y－z坐标表示整体坐标系，x'－y'－z'坐标表示杆的单元坐标系，杆单元的两个节点分别记为i和j，空间位置坐标分别为(xi，yi，zi)和(xj，yj，zj)。L 表示杆长，CX，CY，CZ分别表示杆的轴向方向与 x，y，z轴夹角的余弦，可以用节点坐标表示为:

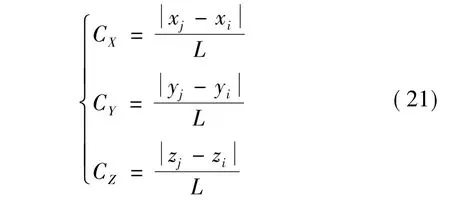
图4中α为杆与其在yz平面内投影的夹角，可以写为:

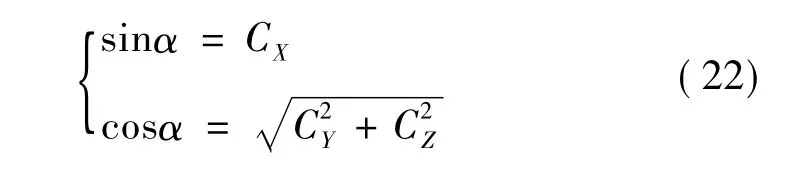
对比图3与图4，可以看出，如果空间桁架杆仅受水平地震作用，则杆的地震等效波谱节点荷载就可以通过式(20)计算得到。

考虑实际计算时，杆的节点荷载通常在整体坐标下给出，对式(20)中的地震等效波谱节点荷载进行进一步分解(如图5所示)，整体坐标系下地震等效波谱节点荷载各分量可以表示为:

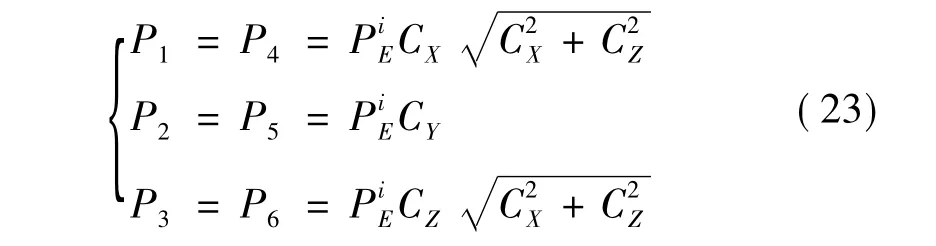
利用式(23)得到的整体坐标系下的地震等效波谱节点荷载作为集中荷载，代入传统的波谱单元法中，即可求得空间桁架结构的地震响应。

4 波谱单元法的计算框架

4.1 荷载向量Laplace变换及位移向量Laplace逆变换

由于FFT变换的周期性，采用基于FFT的波谱单元法主要用来求解半无限长和无限长构件［7］。本文采用文献［7］中的方法，利用数值Laplace变换代替FFT变换，回避了FFT变换周期性问题。

利用FFT实现数值Laplace变换荷载，频域内的荷载向量可以表示为［7］

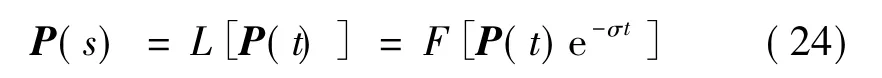
式中P(t)为时域内的节点荷载向量;P(s)为频域内的节点荷载向量;L为Laplace变换算子;F为FFT变换算子;s=σ+iω为Laplace变换参数;其中σ为Laplace变换的实常数;ω为Laplace变换后对应的角频率。

由式(24)可知，时域内节点荷载向量P(t)的Laplace变换可以利用调制后的荷载向量P(t)e－σt通过FFT变换实现。

频域内的位移向量通过Laplace逆变换即可得到时域内的位移向量。Laplace逆变换过程可以表示为［7］:

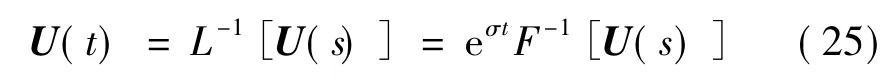
式中U(s)为频域内的节点位移向量;U(t)为时域内的节点位移向量;L－1为 Laplace逆变换算子;F－1为快速傅里叶逆变换(IFFT)。

由式(25)可知，时域内的节点位移向量U(t)的Laplace逆变换可以先将频域内的节点位移向量U(s)进行IFFT变换，然后再乘以eσt得到。

4.2 整体坐标系下空间杆的波谱刚度矩阵

式(19)给出了承受轴向节点荷载的平面杆的单元刚度矩阵，考虑到空间桁架杆的节点位移有三个方向(如图5所示)，计算时需要对式(19)中杆的波谱单元刚度矩阵进行扩展，扩展后的单元刚度矩阵为:

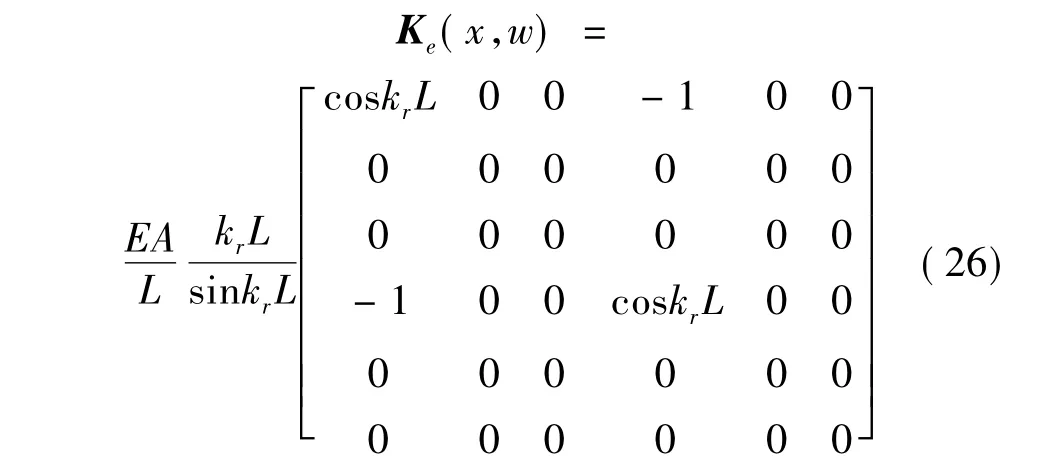
对式(26)中的波谱单元刚度矩阵进行坐标变换，即可得到整体坐标系下的波谱单元刚度矩阵:

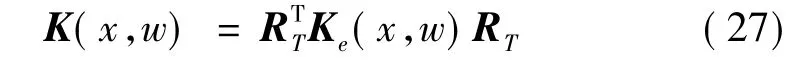
式中RT为文献［11］中给出的空间桁架的转轴变换矩阵，Ke(x，w)为扩展后的波谱单元刚度矩阵，K(x，w)为整体坐标系下的波谱单元刚度矩阵。

4.3 整体波谱矩阵方程

把式(23)中的单元节点荷载写成向量形式:

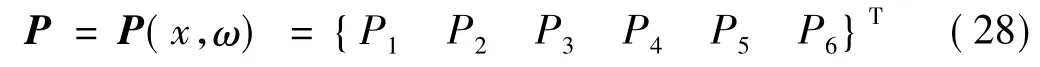
同理，单元节点位移也可写成向量形式:

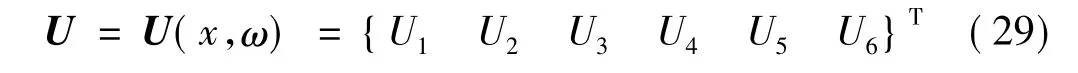
则杆的波谱单元矩阵方程可以表示为:

得到杆的波谱单元矩阵方程后，采用与有限元法相同的分析思路，在频域内将单元刚度矩阵组装成整体刚度矩阵，将单元节点位移向量和单元节点荷载向量分别组装成整体节点位移向量和整体节点荷载向量，组装后的整体波谱矩阵方程可以表示为:

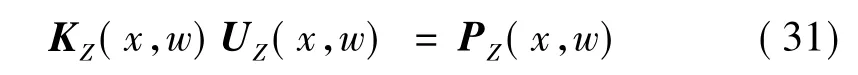
4.4 波谱单元法计算流程

波谱单元法中单元刚度矩阵的组装及矩阵方程的求解都与有限元法的计算过程类似，波谱单元法的计算思路可以用以下的流程图概括:

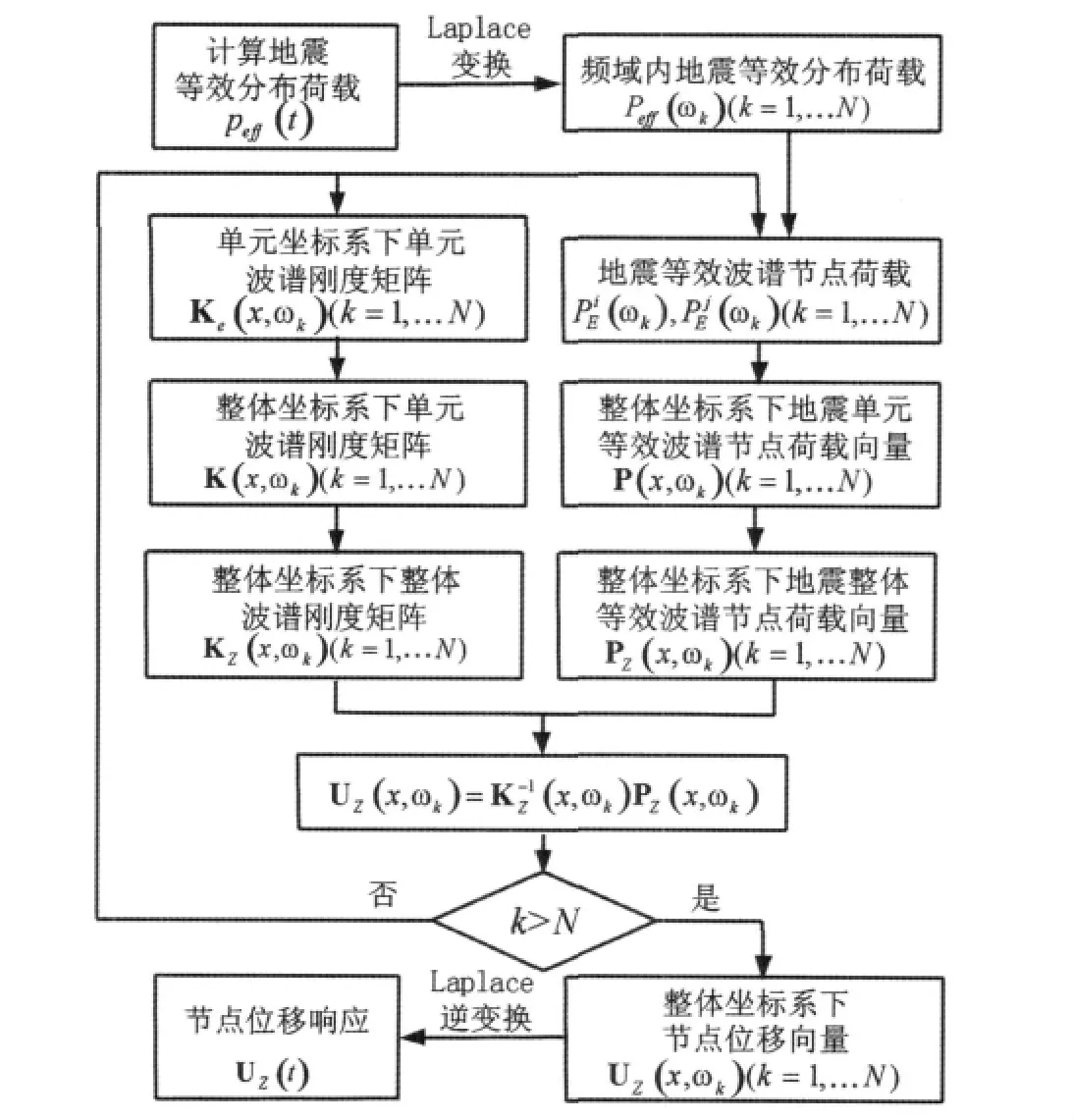
图6 波谱单元法计算流程图Fig.6 A typical flowchart for spectral element method

5 数值算例

5.1 数值算例1

采用波谱单元法和划分不同单元数的有限元法计算图7所示的钢桁架桥中点P点的竖向位移响应，有限元法采用的是Newmark积分［12］。计算时选取的地震波为EI Centro波。Laplace变换的采样时间取为地震波的时间步长ΔT=0.02 s，采样点数N=2 048，计算时长为 T =NΔT =40.96 s，变换实常数 σ=2πNΔT［7］。计算时假定杆的外部粘滞阻尼系数为 α1=0.01，内部粘弹性阻尼系数为 c=0.000 1。杆的尺寸如图7所示，截面尺寸及参数见表1。

表1 钢桁架桥杆截面尺寸及材料参数Tab.1 Size and material properties of steel truss bridge

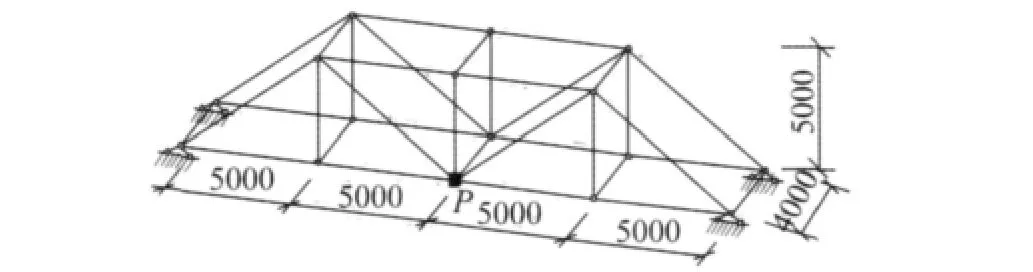
图7 承受竖向地震荷载的钢桁架桥Fig.7 Steel truss bridge subjected to vertical seismic load

图8为波谱单元法和有限元法计算得到的15 s～20 s内竖向位移响应的对比图。波谱单元法每根杆划分1个计算单元，有限元法中每根杆件分别划分为1个、5个、20个、50个单元。

从图8(a)可以看出，有限元法每根杆划为1个单元时的计算结果与波谱单元法的计算结果相差很大。但随着有限元法中划分单元数的增加，有限元法计算结果越来越接近波谱单元法的结果，如图8(a)－图8(d)所示。从图8(d)可以看出，桁架结构每根杆件划分为50个单元时有限元法的计算结果与波谱单元法的结果已经比较接近了。

为便于比较波谱单元法计算结果与有限元法计算结果的差值，引进均方根指标(RMSD)进行评价，均方根指标可以定义为［13］:

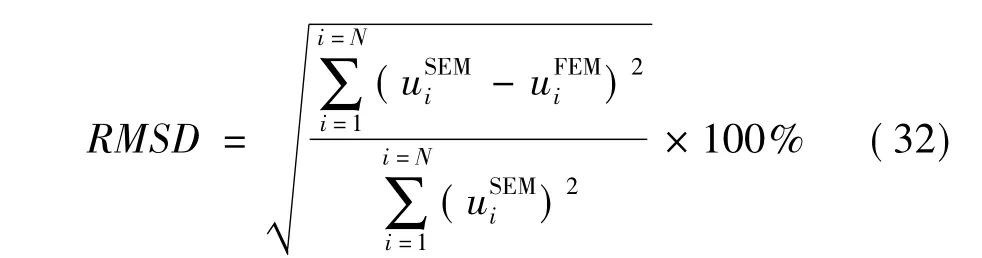
式中uSEMi为波谱单元法计算的位移;uFEMi为有限元法计算的位移，i表示第i个离散时间点。

为了比较波谱单元法与有限元法的计算速度，在同一计算机，相同的运行环境下，对两种方法的计算时间进行测试。表2给出了波谱单元法与划分不同单元数的有限元法计算时间及相应的均方根指标。可以看到，随着有限元法划分单元数的增加，均方根指标逐渐变小，说明有限元分析的结果随着划分单元数的增加在逐渐逼近波谱单元法的计算结果，与传统有限元法相比波谱单元法具有很高的计算精度。

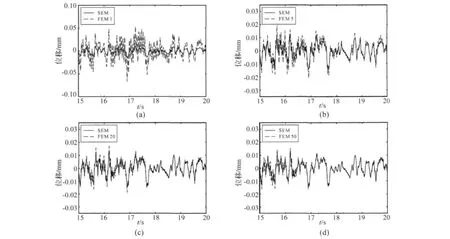
图8 波谱单元法与不同单元数的有限元法计算竖向位移响应图Fig.8 Comparison of vertical displacements calculated by SEM and FEM meshed with different number of elements

由于基于连续质量体系的波谱单元法能大大减少计算单元数量［2］，因而与传统有限元法相比，波谱单元法能有效的缩短计算时间。桁架桥在划分6 800个单元的情况下，采用有限元法计算时间为波谱单元法计算时间的59.36倍，但仍未达到波谱单元法的计算精度。即使与传统有限元法划分相同单元数的情况下，波谱单元法由于计算时无需按时间步长进行积分计算，仍然能减少计算时间。对于本算例中的桁架桥，在划分单元数相同的情况下，波谱单元法计算时间约为有限元法计算时间的1/11。

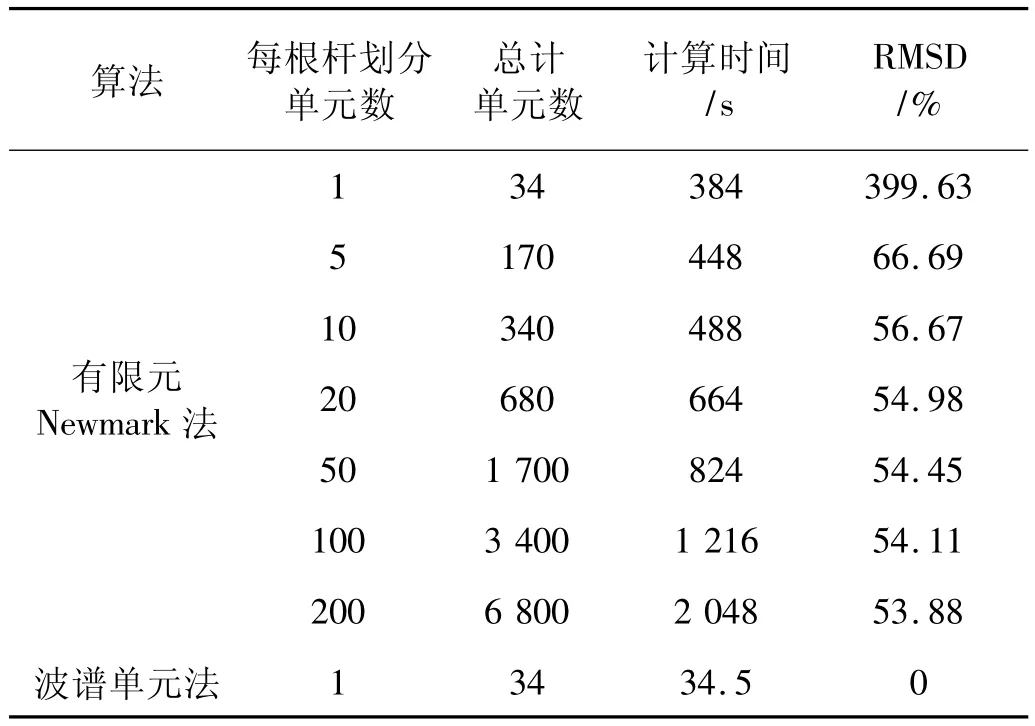
表2 谱单元法与有限元法计算竖向位移结果对比Tab.2 Comparison of vertical displacements calculated by SEM and FEM

图9 承受横向地震荷载的空间桁架Fig.9 Space truss subjected to horizontal seismic load

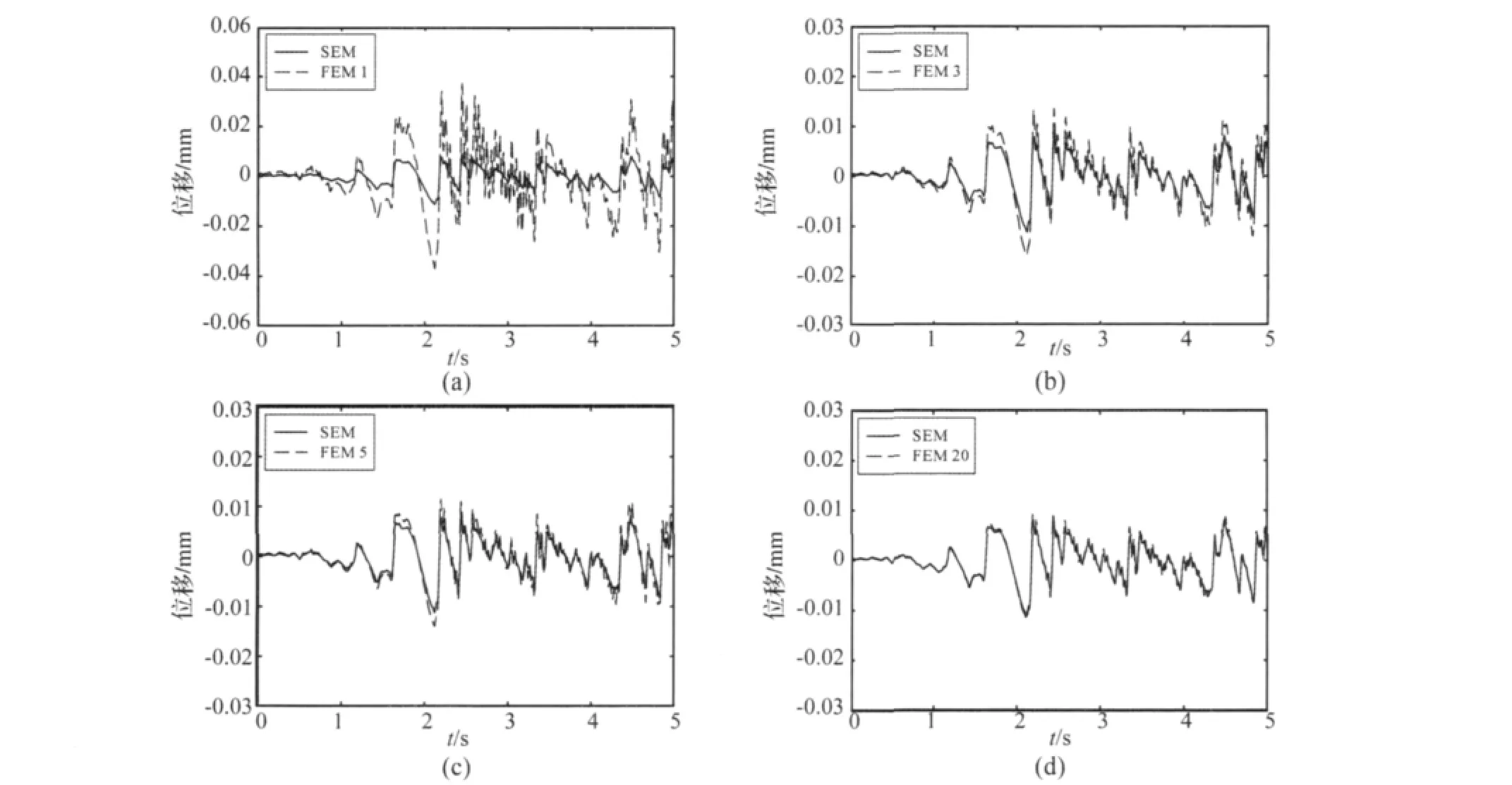
图10 波谱单元法与不同单元数的有限元法计算横向位移响应图Fig.10 Comparison of horizontal displacements calculated by SEM and FEM meshed with different number of elements

5.2 数值算例2

分析图9所示的空间桁架结构在水平地震荷载作用下的响应。此处地震荷载仍输入EI Centro波。波谱单元法采用的Laplace变换参数及假定的桁架杆的阻尼系数都与算例1相同。桁架杆截面相关参数见表3。

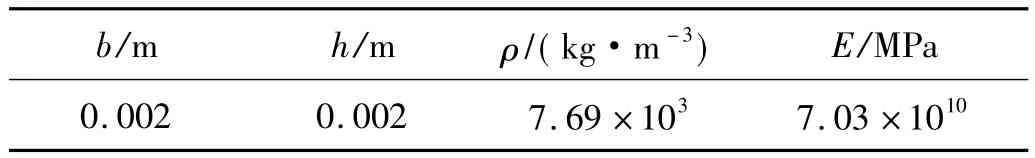
表3 空间桁架杆截面尺寸及材料参数Tab.3 Size and material properties of Space truss

利用波谱单元法对图9所示的空间桁架结构进行分析，每根杆件作为1个计算单元。采用有限元法分析时，每根桁架杆分别划分为1个、3个、5个、20个计算单元。图10对比了通过波谱单元法和有限元法计算桁架下弦中心O点水平位移前5s响应。可以看出，随着有限元法中划分单元数的增加，有限元法计算结果越来越接近波谱单元法的结果。桁架结构每根杆件划分为20个单元时计算得到的O点水平位移曲线与波谱单元法的计算曲线大致重合，如图10(d)所示。

表4给出了波谱单元法与划分不同单元数的有限元法计算时间及相应的均方根指标。与算例1一样，随着有限元法划分单元数的增加，均方根指标逐渐变小，表示有限元法的计算结果将随计算单元数量增加逐渐逼近谱单元法结果。对于算例2，划分相同单元数时，谱单元法计算时间约为有限元法的1/6，而每根杆划分150个单元时，有限元法计算的时间约为谱单元法计算时间的101倍。算例2再次有效的说明了采用本文改进后的波谱单元法来计算桁架的地震响应，不仅能大大改善计算精度，而且能有效提高计算效率，减少计算时间。

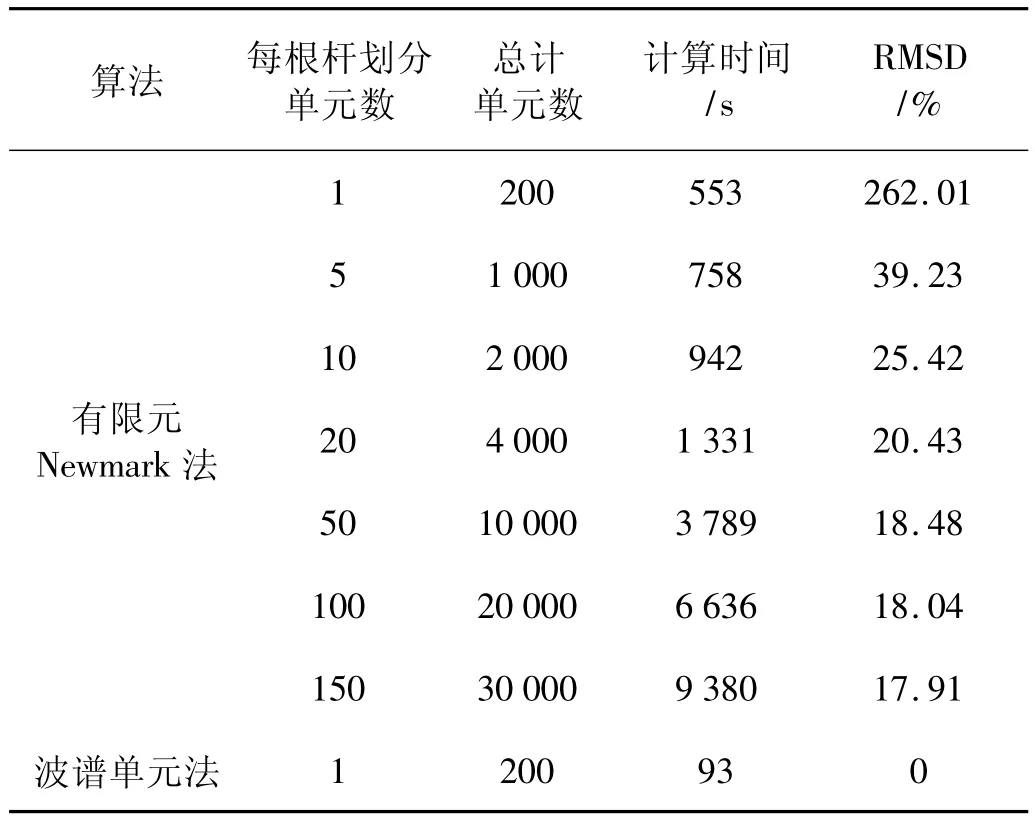
表4 谱单元法与有限元法计算水平位移结果对比Tab.4 Comparison of horizontal displacements calculated by SEM and FEM

6 结论

本文基于虚功原理，通过波谱形函数积分推导了桁架结构在地震荷载作用下等效波谱节点荷载的显式表达式。在波谱单元法中利用等效后的节点荷载对EI-Centro波作用下的空间桁架进行地震响应分析。分析结果表明，通过荷载等效的方式，能十分方便进行编程计算，精确求解结构的地震响应。采用基于Laplace变换的波谱单元法能有效回避FFT的周期性问题，无需加上无限长单元即可以精确求解有限长结构。通过修改波谱单元法中的波数，可以简便的在波谱单元法中考虑阻尼的影响。与传统有限元法相比，波谱单元法能大大减少单元数量并提高计算精度。

［1］Lee U.Vibration analysis of one-dimensional structures using the spectraltransfermatrix method ［J］. Engineering Structures，2000，22:681－690.

［2］Dolyle J F，Farris T N.A spectrally formulated finite element for flexural wave propagation in beams［J］.The international journal of Analytical and Experimental Modal Analysis，1990，5(2):99－107.

［3］Lee U，Kim J H，Leung A Y T.The spectral element Method in Structural dynamics［J］.The Shock and Vibration Digest，2000，32(6):451－465.

［4］Dolyle J F，Farris T N.A spectrally formulated finite element for wave propagation in 3 －D frame structures［J］.The international journal of Analytical and Experimental Modal Analysis，1990，5(4):223 －237.

［5］Dolyle J F.A spectrally formulated finite element for longitudinal wave propagation［J］.The international journal of Analytical and Experimental Modal Analysis.1988，3(1):1－5.

［6］Cho J Y，Go H S，Lee U.Dynamic response of the spectral element model by using the FFT［J］.2007，345－346:845－848.

［7］Igawa H，Komatsu K，Yamaguchi I et al.Wave propagation analysis of frame structures using the spectral element method［J］. Journalofsound and vibration， 2004， 277:1071－1081.

［8］Lee U，Lee J K.Spectral element analysis of the structure under dynamic distributed loads［J］.Journal of Mechanical Science and Technology，1998，12(4):565－571.

［9］Lee U，Cho J Y.FFT-based spectral element analysis for the linear continuum dynamic systems subjected to arbitrary initial conditions by using the pseudo-force method ［J］.International Journal for Numerical Methods in Engineering，2007，74(1):159－174.

［10］R.克拉夫，J.彭津.结构动力学［M］.王光远 等译.北京:高等教育出版社，2006.

［11］刘树棠.杆系结构有限元分析与matlab应用［M］.北京:中国水利水电出版社，2007.

［12］王元汉，李丽娟，李银平.有限元法基础与程序设计［M］.广州:华南理工大学出版社，2001.

［13］ Soh C K，Tseng K K H，Bhalla S，et al.Performance of smart piezoceramic patches in health monitoring of a RC bridge［J］.Smart Materials and Structures，2000，9(4)，533－542.

Application of spectral element method in dynamic analysis of a space truss subjected to seismic load

ZHANG Jun-bing1，2，ZHU Hong-ping1，2，WANG Dan-sheng1，2，GE Dong-dong1，2

(1.School of Civil Engineering＆ Mechanics，Huazhong University of Science＆ Technology，Wuhan 430074，China;2.Hubei Key Laboratory of Control Structure，Huazhong University of Science＆ Technology，Wuhan 430074，China)

An extended spectral element method(SEM)was established to get dynamic responses of a space truss subjected to seismic load.The seismic load was equivalent to concentrated node forces by integrating the shape function in SEM based on the principle of virtual work.Both internal viscoelastic damping and external viscous damping of the truss bar were considered by just simply modifying the wave number.Laplace transformation instead of fast Fourier transformation(FFT)was utilized in SEM to avoid the periodicity of FFT.To evaluate the accuracy of Laplace-based SEM，the dynamic responses of a space truss under seismic load was analyzed as a numerical example.The numerical results obtained using FEM were compared with those using SEM.It was found that SEM provides good dynamic results under seismic load;the equivalent seismic node forces are convenient to get by programming calculation;SEM is proved to be an efficient method to analyze dynamic responses of structures accurately while the number of element greatly decreases.

spectral element method(SEM);damping;wave number;space truss;FEM;seismic responses

TU311.3;TU323.4

A

国家杰出青年基金(50925828);国家自然科学基金资助项目(50778077);高校博士学科点专项科研基金(20070487099)

2009－12－18 修改稿收到日期:2010－03－05

张俊兵 男，博士，1985年2月生