不等式约束对平差结果的影响分析
朱建军,谢 建,陈宇波
中南大学地球科学与信息物理学院,湖南长沙410083
1 引 言
在数据处理的许多情况下可根据先验知识建立对参数的某种约束,如果所建立的约束是不等式形式,则形成了具有不等式约束的平差问题。对附不等式约束的平差问题近年来有众多学者进行了一系列研究。文献[1-4]都曾研究过用高程约束改善GPS模糊度的分解,文献[5]将附不等式约束的问题作为一种平差模型提出,并研究其解算方法。文献[6]通过罚函数的思想提出附不等式约束平差模型解算的凝聚函数法。文献[7]提出用遗传算法和Matlab的优化工具箱解决附不等式约束的计算问题。文献[8]基于Kuhn-Tucker条件提出一种拉格朗日乘子迭代算法。文献[9]从线性补的角度研究带有线性不等式约束平差模型的算法。文献[10]研究了不等式约束在GPS变形测量中的应用。文献[11]将不等式约束的平差模型统一到经典平差模型中。但是,目前这些研究主要是集中在附不等式约束平差模型的解法上,也就是如何获取参数的最优估值。由于附不等式约束的平差模型求解时,平差参数不能表达成观测值的函数,不能用传统的平差方法和平差知识求解,因而采用附不等式约束平差模型时,不等式约束对平差结果的贡献(影响)及平差参数的统计性质等还不是十分明了。
针对这一问题,根据附不等式约束的平差过程,利用概率统计的思想,分析不等式约束对平差结果的影响,从而分析平差结果的有关统计性质。最后以一个简单的例子直观验证了有关分析和结论。
2 附不等式约束对平差结果的影响分析
2.1 经典平差模型的解及精度
无约束的平差模型(误差方程)可以表示为

式中,L为观测值;V为观测改正数;X为未知数;A为系数矩阵;P为观测权矩阵。在最小二乘准则下,可以得到
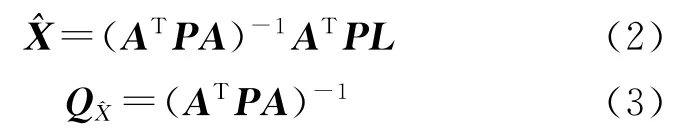
2.2 附不等式约束平差模型的影响分析
若有不等式约束GX≤W,则附不等式约束的平差模型可以表示为
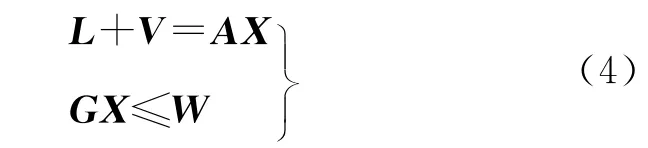
不等式约束GX≤W在几何空间上来说,是一个区域(如图1)。

图1 不等式约束的几何描述Fig.1 Geometrical description of inequality constraints

对于第二种情况,解将位于由Q^X确定的椭圆与不等式约束所限定的区域S的切点上[5],即解将落在不等式约束所限定的区域的边沿GX=W上。不等式约束的作用就是将无约束时落在区域外的解通过Q^X确定的椭圆全部投影到约束区域的边缘上。无约束时,解落在任意一点的频率为f(X)。有不等式约束时,解落在不等式约束作用的区域之外时将会通过Q^X确定的椭圆全部投影到约束区域的边缘上,所以实际落在区域之外的频率将为0,而落在区域边缘上的频率不再是f(X),将会是
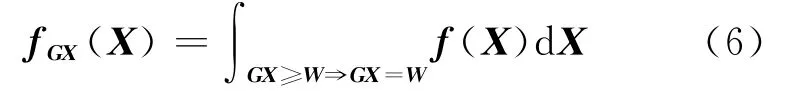
式中,GX≥W⇒GX=W表示从区域外到区域边缘的投影,即区域外的频率全部投影到了区域边缘,并且有
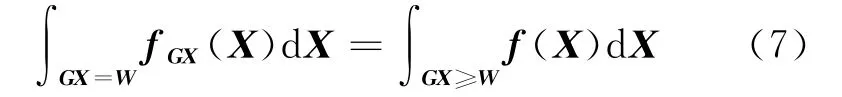
上式左边表示沿区域边沿的积分,右边表示区域外的积分。附不等式约束平差解的验后分布就可表示为
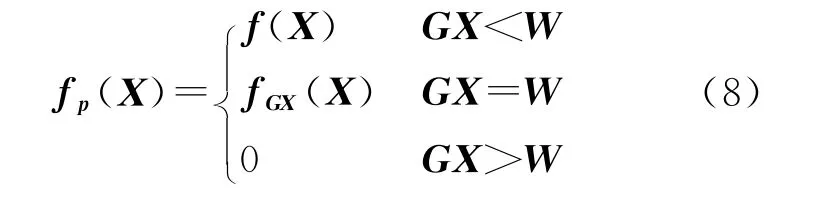
验后均值为
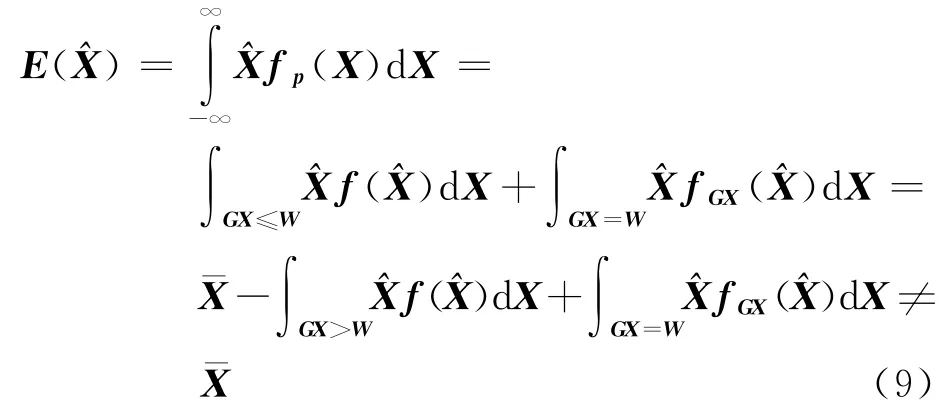
验后均方误差为

由式(9)、式(10)可以看出:
(1)模型(4)的估计是有偏的。式(9)中的第二项和第三项是由于不等式约束引起的,如果没有不等式约束,则期望值为为无偏。式(9)第二项为X在约束区域外的积分,而第三项为X在区域边沿的积分上。如果这两个积分本身不为0的话(非对称),这两部分一般是不会相等的,因而期望值不会等于真值,其偏差为

很显然,该偏差是由于不等式约束破坏了验后分布的对称性造成的,其大小取决于误差本身的分布及不等式约束的非对称性。如果观测无误差,则
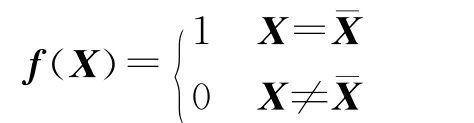
此时,式(9)右边第二、三两部分的积分都将为0,上述偏差为0,估计仍然无偏。故这种估计有偏是因为不等式约束打乱了平差参数验后(误差)分布的均匀性而产生的,性质与观测中含系统误差类似,与数学中有偏估计方法得到的有偏估计却不相同。数学中的有偏估计方法得到的是压缩估计,即使观测没有误差,估计也是有偏的。
(2)附不等式约束平差的解的均方误差恒定小于无约束的最小二乘解。由于附不等式约束平差估计的期望值受误差分布的不均匀影响,方差就不能完全反映估计的精确程度,按传统平差衡量待估参数质量的方法,即估计值与真值的差异程度,选估计的均方误差作为估计质量的评价标准,附不等式约束平差解的均方误差由式(10)表示。显然,只要真值位于不等式约束区域之内,则以真值为中心向外发散的每一条射线上,式(10)第二部分的积分都会大于等于第三部分的积分,即上式第二、三部分之和小于或等于0。附不等式约束平差模型解的均方误差恒小于或等于无约束平差时解的方差。
(3)从精度的角度来说,不等式约束,不管是不是有效约束,总是有用的。在式(9)、式(10)的积分中,所有的约束,不管是有效约束还是无效约束都对积分起作用,所以不管是不是有效约束,都是有用的。
(4)约束对解的贡献(或影响)与其约束值到真值的距离有关,约束值到真值的距离越小,对解的贡献越大,反之越小。式(9)第二、三两部分的差值与约束离真值的距离有关。如果约束与真值的距离很远,例如大于3σ,那么由正态分布的定义可知,f(X)或fGX(X)在远离期望的地方都会取到很小的值,式(9)的第二、三部分的贡献就都会很小,约束的作用就不大。
3 算例分析
下面以一个极为简单的一维例子直观说明上述不等式约束对平差结果影响规律的分析。
假定有A、B两点之间的距离需要确定,由某种先验知识可以确定AB之间的距离X应该在a,b之间,即大于a小于b。用测距仪对AB距离进行测量,得观测值L,L的精度为σ,如果只对AB进行1次观测,平差模型(4)可表示为
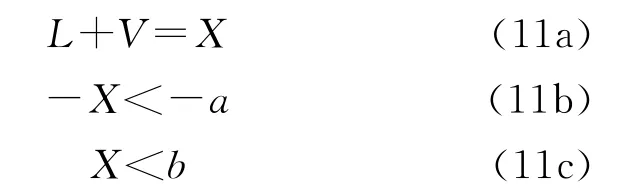
该模型的解可表示为^XIneq,假定观测误差服从正态分布,观测值的取值则按图2分布。
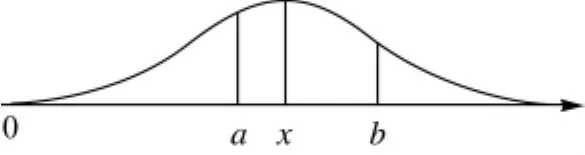
图2 观测误差分布与不等式约束解Fig.2 Observation error distribution and solution to inequality constrained adjustment

在没有不等式约束的情况下,式(11)的最小二乘解为^X=L,考虑不等式约束后,按上一节的分析,分成两种情况:一是无约束最小二乘解满足不等式约束,即a<L<b;二是无约束最小二乘解不满足不等式约束或至少有一个约束不满足,在本例中,可再分为观测值落在区间L>b和观测值落在区间L<a两种情况。
第一种情况是观测值落在区间a<L<b,此时,约束条件(11b)(11c)都满足,不等式约束为无效约束,模型(11)等价于无约束的最小二乘模型,其解为
第二种情况,当观测值落在区间L>b,此时,无约束的最小二乘解为约束条件(11c)不满足,为有效约束,约束条件(11b)满足为无效约束。按有效约束方法,上述平差模型的解等价于由下面的附等式的平差模型求得的解即在不等式约束的约束下,解取的概率为Pb,在这种情况下,无约束解的取值范围仍然在区间(b,+∞),不等式约束(11c)的作用就是把无约束时落在区间(b,+∞)的解投影到不等式约束区间的边界(端点)b上。
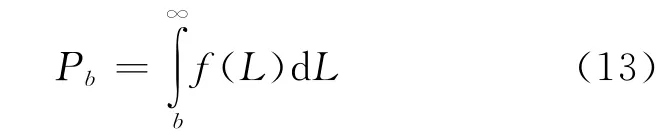

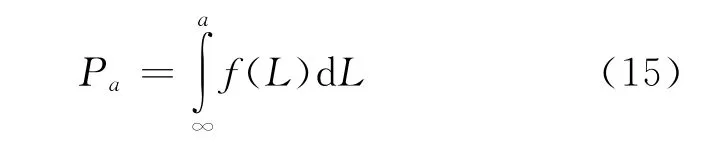
在本例的一维情况下,附不等式约束解的验后分布,即式(8)为
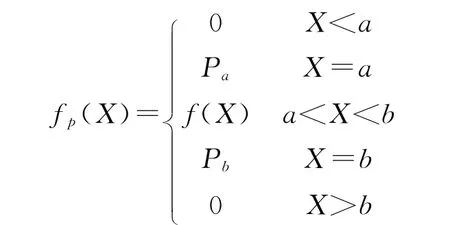
期望值,即式(9)可表示为
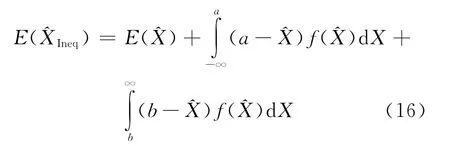
式(10)可表示为
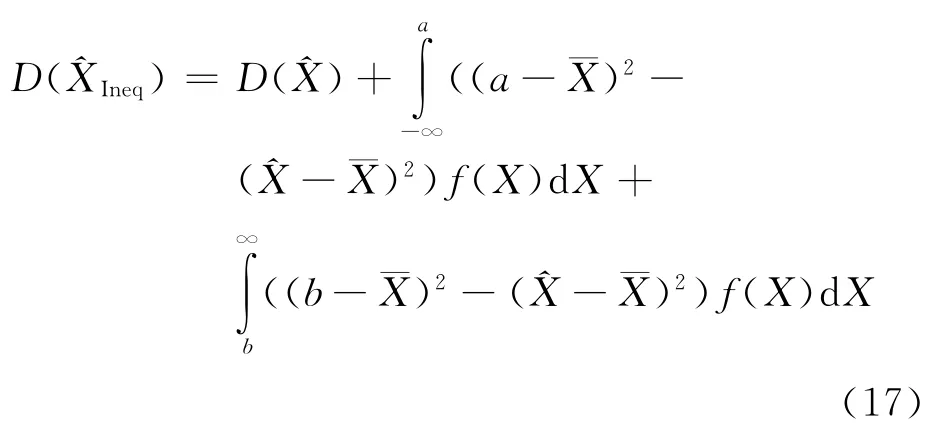
很显然,式(16)第二、三项之和只有在a、b与未知数真值对称时才会为0,一般情况下不为0,即一般情况下^XIneq是有偏的。由图2可知,只要不等式约束是正确,在区间(-∞,a)恒定有在(b,+ ∞)恒定有即式(17)第二、三项恒定的小于是恒定成立的。
在式(17)中,第二项代表约束(1)对解的精度的贡献,第三项代表约束(2)对解的精度的贡献。如果观测落在区间(-∞,a),约束(11b)为有效约束,约束(11c)为无效约束,如果观测落在区间(b,+∞),则约束(11c)为有效约束,约束(11b)为无效约束,如果观测落在区间(a,b)那么约束(11b)、(11c)都为无效约束。但不管观测落在哪个区间,式(17)第二、第三项都会小于0,都对解的精度有贡献。贡献的大小与约束值a、b到真值的距离有关,约束值到真值的距离越小,对解的贡献越大,反之越小。
以约束(11b)为例,约束(11b)对解精度的贡献为式(17)中的第二项,分别取结果如表1。
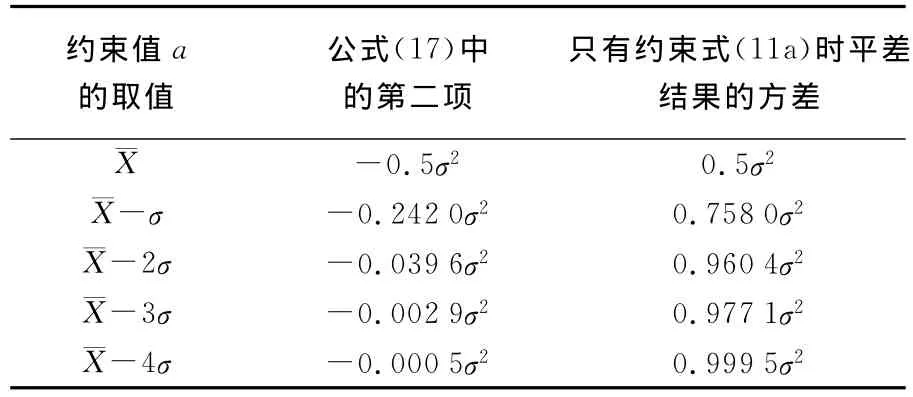
表1 约束值距离真值的远近对平差结果的影响Tab.1 The affect of the distance between constrained and real value to the adjustment results
可以看出,不等式约束区间离真值3倍中误差以上,其对解的贡献就非常有限了。这在直观上是很好理解的。比方说要测量地球到月球的距离,附加一不等式约束:地球到月球的距离大于1mm,很显然这一约束是绝对正确的,但也毫无意义。这一结论主要说明,不同的不等式约束对解的作用不相同,不等式约束必须与观测精度相适应才能起作用。
对于上述第一种情况,约束条件(11c)为有效约束,附不等式约束的平差模型(11)的解与附等式的平差模型(12)的解相同。但此时,附不等式约束的平差模型(11)的解的方差是由式(17)确定,并且肯定不会为0,但模型(12)的解的方差确为0。同样对第二种情况也有同样的结论。因此在找到有效约束后,视有效约束为等式约束来评定附不等式约束的解的精度是显然不合理的。
4 结 论
由式(9)、式(10)及上面的算例,可以得到以下结论:
(1)附不等式约束平差模型的解是有偏的,这种估计有偏是因为不等式约束打乱了平差参数验后(误差)分布的均匀性而产生的,性质与观测中含系统误差类似,不同于数学中压缩型有偏估计。压缩型有偏估计即使观测没有误差,估计也是有偏的。
(2)附不等式约束平差时,其解的方差恒定小于无约束的最小二乘解。
(3)不管不等式约束是有效约束还是无效约束,对最后的解的精度都有贡献。
(4)不同的约束对解的贡献不同,各约束对解的贡献与其约束到真值的距离有关,约束到真值的距离越小,对解的贡献越大,反之越小。
(5)有效约束在求解时与等式约束等价,但在评定精度时与等式约束不等价。
[1] REMONDI B W.Real Time Centimeter-accuracy GPS:Initializing while in Motion(Warm Start Versus Cold Start)[J].Navigation,1993,40(2):199-208.
[2] UENO M,SANTERRE R,LANGELIER D,et al.Improvement of GPS Ambiguity Resolution Using Height Constraint for the Support of Bathymetric Surveys[C]∥Proceedings of the IAIN/ION Conference.San Diego:[s.n.],2000:842-850.
[3] ZHU Jianjun,SANTERRE R.Improvement of GPS Phase Ambiguity Resolution Using Prior Height Information as a Quasi-observation[J].Geomatica,2002,56(3):211-221.
[4] LU G,KRAKIWSKY E J,LACHAPELLE G.Application of Inequality Constraint Least Squares to GPS Navigation under Selective Availability[J].Manuscripta Geodaetica,1993,18:124-130.
[5] ZHU Jianjun,SANTERRE R,CHANG Xiaowen.A Bayesian Method for Linear Inequality Constrained Adjustment and Its Application to GPS Positioning[J].Journal of Geodesy,2005,78(9):528-534.
[6] PENG Junhuan.An Aggregate Constraint Method for Inequality-constrained Least Squares Problem[J].Journal of Geodesy,2006,79(12):705-713.
[7] ZHU Jianjun,OUYANG Wensen,WEN Xiaoyue.Solving the LICA Problem by GA Method[J].Journal of Geotechnical Investigation &Surveying,2006(3):61-65.(朱建军,欧阳文森,文小岳.基于遗传算法解决附有不等式约束的最小二乘平差问题的研究[J].工程勘察,2006(3):61-65.)
[8] FENG Guangcai,ZHU Jianjun,CHEN Zhengyang,et al.A New Approach to Inequality Constrained Least-squares Adjustment[J].Acta Geodaetica et Cartographica Sinica,2007,36(2):119-123.(冯光财,朱建军,陈正阳,等.基于有效约束的附不等式约束平差的一种新算法[J].测绘学报,2007,36(2),119-123.)
[9] SONG Yingchun,ZUO Tingying,ZHU Jianjun.Research on Algorithm of Adjustment Model with Linear Inequality Constrained Parameters[J].Acta Geodaetica et Cartographica Sinica,2008,37(4):433-437.(宋迎春,左廷英,朱建军.带有线性不等式约束平差模型的算法研究[J].测绘学报,2008,37(4):433-437.)
[10] DAI Wujiao,ZHU Jianjun,DING Xiaoli,et al.Single Epoch Ambiguity Resolution in Structure Monitoring Using GPS[J].Geomatics and Information Science of Wunan University,2007,32(3):234-237.(戴吾蛟,朱建军,丁晓利,等.GPS建筑物振动变形监测中的单历元算法研究[J].武汉大学学报:信息科学版,2007,32(3):234-237.)
[11] OUYANG Wensen,ZHU Jianjun.Expanding of Classical Surveying Adjustment Model[J].Acta Geodaetica et Cartographica Sinica,2009,38(1):12-15.(欧阳文森,朱建军.经典平差模型的扩展[J].测绘学报,2009,38(1):12-15.)
[12] SHENG Zhou,XIE Shiqian,PAN Chengyi.Theory of Probability and Mathematical Statistics[M].Beijing:Higher Education Press,2003.(盛骤,谢式千,潘承毅.概率论与数理统计[M].北京:高等教育出版社,2003.)

