面积问题的解法探究和思考

226364 江苏南通通州区赵甸初中 金建华

面积问题的解法探究和思考

226364 江苏南通通州区赵甸初中 金建华

1 问题的提出

原题 (2010年四川绵阳)如图1，抛物线 y=ax2+bx+4与x轴的两个交点分别为 A(－4，0)，B(2，0)，与 y轴交于点 C，顶点为 D.E(1，2)为线段BC的中点，BC的垂直平分线与x轴，y轴分别交于F，G.(1)求抛物线的函数解析式，并写出顶点D的坐标;(2)若点K在x轴上方的抛物线上运动，当K运动到什么位置时，△EFK的面积最大?并求出最大面积.

图1

答案的质疑与思考 本题条件是“点K在x轴上方的抛物线上”，但参考答案只对“xF＜t＜xE”作了解答，那么“xA＜t≤xF”，“xE≤t＜ xB”会怎么样呢?笔者认为这是一个名副其实的“参考答案”，不够严谨.如果要完整地解答此题就必须分类讨论，分类表示S△EFK又是一个复杂的问题.

像这样的面积问题是近几年中考的热点之一，常结合一次函数、二次函数、四边形、相似形等知识而命题，具有一定的综合性.笔者研读了2009年和2010年部分中考试题及解答，一般都通过分割，建立面积函数，用函数知识解决问题.这些分割方法通常比较麻烦，有时还回避不了分类讨论.

2 解法探究

2.1 寻源

书本习题 人教版教科书91页习题19.1第8题:如图 2，直线 l1∥l2，△ABC和△DBC面积相等吗?你还能画出一些与△ABC面积相等的三角形吗?

解 显然，△ABC和△DBC面积相等，原因是这两个三角形同底等高.直线l1上任意一点P与B，C两点构成的△PBC与△ABC面积总相等.

启示 此题可以通过平行线，把三角形等积变形为其他更有利于解决问题的三角形.

2.2 探究

笔者进一步研究发现，这些问题通常可以分为两类，都可以用简单的平移法来解决.

2.2.1 动点在直线上，利用平行线，通过等积变形建立函数模型

图2

例1 (2009年济南)已知:如图3，抛物线 y=ax2+bx+c( a≠0)的对称轴为x=－1，与 x轴交于 A，B两点，与 y轴交于点 C，其中A(－3，0)，C(0，－2).

(1)求这条抛物线的函数表达式;

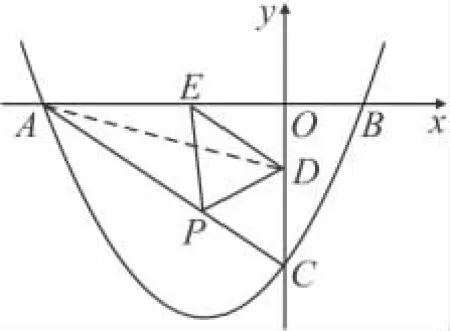
图3

(2)若点D是线段OC上的一个动点.过点D作DE∥PC交x轴于点E.设CD的长为m，△PDE的面积为S.求S与m之间的函数关系式.试探讨S是否存在最大值，说明理由.

点评 本题的动点D在直线上运动，没有采用分割的方法也没有分类讨论，而是利用题目原有的DE∥PC条件，把△PDE等积变形为一边在坐标轴上的△ADE，便于表示△PDE的面积，建立函数模型解决问题.

例2 (2010年三明)如图4，已知抛物线y=ax2+bx+c(a≠0)经过点 B(2，0)和点C(0，8)，且它的对称轴是直线x= －2.

(1)求抛物线与x轴的另一交点A的坐标;

(2)求此抛物线的解析式;

(3)连接AC，BC，若点E是线段AB上的一个动点(与点A，点B)不重合，过点E作EF∥AC交BC于点F，连接CE，设AE的长为m，△CEF的面积为S，求S与m之间的函数关系式;

(4)在(3)的基础上探讨S是否存在最大值，说明理由.

解 (1)A点的坐标为(－6，0);

图4

(3)过点F作FG⊥AB，垂足为G，

解题策略 以上两例都是动点在直线上运动，利用天然的平行条件，通过等积变形，把三角形转化为有一边在坐标轴上的三角形，从而比较简洁地建立函数模型，应用函数知识解决问题.不必分割，不必分类.

2.2.2 动点在抛物线上动，构建平行线，通过等积变形建立方程模型

例3 (2010年恩施)如图5，二次函数y=x2+bx+c的图象与x轴交于 A，B(3，0)两点，与y轴交于C(0，－3)点，点 P是直线BC下方的抛物线上一动点.

(1)求这个二次函数的表达式;

(2)当点P运动到什么位置时，四边形ABPC的面积最大并求出最大面积.

解 (1)函数表达式为y=x2－2x－3.

(2)∵S△ABC=6，∴当△BPC的面积最大时，

四边形ABPC的面积最大.

作 PQ∥BC 交 y轴于点 Q，则 S△BPC=S△BQC，△BQC的高OB为定值，所以当PQ平移到使得CQ取得最大值时，△BQC的面积最大，此时直线PQ和抛物线恰好一个公共点.设直线PQ:y=x+m，得方程

图5

点评 本例是动点在抛物线上运动，没有天然的平行条件，采用构造平行线的方法，等积变形为有一边在坐标轴上的图形，建立方程模型解决问题.

例4 (2010年宜宾)如图6，将直角边长为6的等腰Rt△AOC放在平面直角坐标系中，点O为坐标原点，点C，A分别在x，y轴的正半轴上，一条抛物线经过点A，C 及点B(–3，0).

(1)求该抛物线的解析式;

(2)若点P是线段BC上一动点，过点P作AB的平行线交 AC于点 E，连接 AP，当△APE的面积最大时，求点P的坐标;

图6

2.3 原题的解答

(2010年四川绵阳)

(3)在第一象限内的该抛物线上是否存在点G，使△AGC的面积与(2)中△APE的最大面积相等?请说明理由.

简析 本题的第(2)问是动点P在直线上运动类型，利用天然的PE∥AB条件，把S△APE转化为一边在x轴上的S△BPE，建立函数模型解决问题.第(3)问是动点在抛物线上运动类型，直接求出直线HG的解析式，更显此法的优越性.

解 如图7，探求得F点坐标为(－3，0)，直线EF为y=x+.过K点作EF的平行线，交y轴于M点，设直线KM的解析式为y=x+b，△EFK的边EF为定值，又CE=EB，平移直线KM可知，当KM与抛物线有且只有一个公共点时，△EFK的高取得最大值，从而面积最大.

点评 动点K在抛物线上运动，构建平行线后，虽然不能转化为有一边在坐标轴上的三角形，但是依然可以通过平移直线的方法建立方程模型解决问题.K点和M点虽然都是动点，但却有本质的区别，M点只能在y轴上上下移动，但一定在E，F之间，所以不必分类，但K点却是上下左右都移动，完全有可能不在E，F之间，那就必须分类讨论.

图7

以上解法简单地说就是利用平行线或构造平行线，实际是平移思想的具体运用.用平移的观点看待问题，会使问题显得简单、易理解，许多问题可以通过平移直线来解决.

3 思考

3.1 命题启示

为什么学生采用分割法建立面积函数解决问题?笔者研究发现，一些中考试题要求学生建立面积函数再求最值，这些试题试图给学生思考的台阶，实际却束缚了学生的思维.作为一道好的中考题，应该给学生充分发挥个人才智、展现独特个性、彰显创新成果的空间，中考题是教学的指挥棒，是学生学和教师教的参照标准，中考怎么考，教师就怎么教，学生就怎么学，因此作为命题者一定要慎重!

不严谨的教学、不严谨的答案，都会影响学生的思维，形成学生思维的不严谨性，教师在教学中一定要培养学生严谨的思维习惯，否则会影响学生的后续学习，甚至造成学生为人的不严谨、工作的不严谨，中考题是教师教学的风向标，更应做出“严谨”的标杆.

3.2 教学启示

为什么命题者也给出分割法建立函数求最值?难道这些教育专家不知道这种解法吗?笔者研究发现，课改后，教材新增了平移章节，这是新教材的一大亮点，实际上是提前渗透了平移的思想，培养学生平移的思想观念，才能让学生领悟教材，探索到更好的解题方法.

平移直线的解法来源于对书本简单习题的思考，书本习题是经过教育专家的研究而设立的，其内涵丰富，对强化基础知识和基本技能，开发智力、培养能力以及对后续学习有着不同寻常的作用，研究各地每年的中考试题都会发现书本习题的影子，这启发我们在日常的教学活动中，要加强对课程的研究，重视书本习题的作用，对教材里的习题作适当的补充挖掘，把课本习题用足、用好、用到位，这样才能从教材简单的例、习题中获得解决问题的新思想、新方法，才能引导学生重视教材，同时培养学生探索的能力和创新的意识，达到事半功倍的效果.

20110329)