局部PFI代数

秦学成

（赤峰学院 初等教育学院，内蒙古 赤峰 024000）

局部PFI代数

秦学成

（赤峰学院 初等教育学院，内蒙古 赤峰 024000）

本文主要考察满足条件(P)的Fuzzy蕴涵代数(简称PFI代数)的基本特征.提出了局部PFI代数的概念并研究其性质,获得了PFI代数成为局部PFI的若干充要条件.

模糊逻辑；Fuzzy蕴涵代数；PFI代数；局部PFI代数；MP滤子

1 引言

非经典数理逻辑[1]的一个重要的研究方向是对有关逻辑代数系统的研究.为了证明Lukasiewicz逻辑系统的完备性,C.C.Chang提出并研究了MV代数,同时提出了局部有限MV代数的概念[2].此后,在1993年,L.P.Belluce等将局部有限MV代数的概念加以推广,提出了局部MV代数的概念[3].由于MV代数是一种特殊的BL代数,因此,E.Turunen等又将这一思想推广到BL代数,提出局部BL代数的概念[4].1996年,我国学者王国俊提出了R0代数的概念,考虑到R0代数与MV代数以及BL代数的联系与区别,文[5]提出了局部R0代数的概念并研究其性质.文献[6]中引入的Fuzzy蕴涵代数(简称:FI-代数)逻辑蕴涵连接词的代数化,它揭示蕴涵算子的共同性质.值得注意的是,MV-代数,BL-代数[7],格蕴涵代数[8],R0-代数以及剩余格代数等,都可以看成FI代数的特例,因而对FI代数的研究具有广泛而基本的重要意义,近年来,人们对这一代数结构已做了大量细致的研究工作[9-15].

为了进一步考察FI代数结构特性,本文将C.C.Chang的思想推广到FI代数,提出局部PFI代数的概念并研究其性质,获得了一些有意义的结果.

2 基本概念和基本结果

定义 2.1[6]称（2,0)型代数(X，→,0)为Fuzzy蕴涵代数,简称FI代数,若坌x,y,z∈X有

(I1)x→(y→z)=y→(x→z);

(I2)(x→y)→((y→z)→(x→z))=1;

(I3)x→x=1;

(I4)x→y=y→x=1圯x=y;

(I5)0→x=1.其中 1=0→0.

文献[6],在FI代数中定义了一个偏序≤:x≤y圳x→y=1.另外还定义了元素x的伪补c(x)=x→0.若(X,→,0)是 FI代数,且坌x∈X,cc(x)=x,则称(X,→,0)是正则FI代数.

引理2.1[6,11]设(X,→,0)是一个FI代数.则坌x,y,z∈X有

(1)x≤1 且 1→x=x

(2)如果 x≤y,则 z→x≤z→y 且 y→z≤x→z;

(3)x≤(x→y)→y;

(4)如果 x≤y 且 y≤z,则 x≤z;

(5)c(0)=1,c(1)=0;

(6)x≤cc(x),ccc(x)=;c(x);

(7)如果 x≤y,则 c(y)≤c(x);

(8)(y→z)→((x→y)→(x→z))=1.

定义2.2[10]称FI代数(X,→,0)具有性质(P),若坌x,y∈X,A(x,y)的最小元minA(x,y)存在,其中A(x,y)={z∈X|x≤y→z}.并称具有性质(P)的 FI代数为 PFI代数.

显然,正则FI代数必为PFI代数.为方便起见,记x⊙y=minA(x,y),显然⊙定义了X上的一个适合交换律的二元运算.约定:x1=x,x2=x⊙x,xk+1=xk⊙x，k∈Z+.特别地,如果(X,→,0)是一个正则 FI代数,则有 x⊙y=c(x→c(y)),坌x,y∈X.

引理2.2[10]设(X,→,0)是一个PFI代数,则有坌x,y,z∈X.

(1)x≤y→(x⊙y)且 x⊙(x→y)≤y;

(2)(x→y)⊙(y→z)≤x→z;

(3)(x⊙y)→z=x→(y→z);

(4)x⊙y≤z圳x≤b→c;

(5)x⊙1=x;

(6)a≤b圯a⊙c≤b⊙c;

(7)(x⊙y)⊙z=x⊙(y⊙z);

(8)x⊙c(x)=0 且 0⊙x=0.

定义2.3[14]设(X,→,0)是一个FI代数,覫≠F埭X.如果坌x,y∈X都有

(MF1)1∈F;

(MF2)x,x→y∈F圯y∈F,

则称F是X的MP滤子.

注 2.1[14](1)设(X,→,0)是 FI代数,则易见{1}和X都是X的MP滤子,且X的任意一族MP滤子的交和定向并都还是X的MP滤子;

(2)设(X,→,0)是FI代数且F是X的MP滤子,则F是一个上集;

(3)设(X,→,0)是PFI代数且F是X的MP滤子,则F对⊙是封闭的.

定义2.4[15]设(X,→,0)是一个FI代数且F是X的MP滤子.如果F≠X,则称F是X的真MP滤子.称X的真MP滤子F为素MP滤子,如果坌x,y∈X都有x→y∈F或y→x∈F.称X的真MP滤子F为极大MP滤子,如果对任意MP滤子E而言,F奂E蕴涵E=F或E=L.

注2.2 设(X,→,0)是PFI代数,则F是X的真MP滤子圳0埸F圳坌x∈X,x∈F与c(x)∈F不同是成立.事实上,设F是X的MP滤子且0埸F,如果x∈F 且 c(x)∈F,则 x⊙c(x)∈F,即 x⊙c(x)=minA(x,c(x))∈F.又坌x∈F,x→(c(x)→0)=1,所以 x≤c(x)→0,从而 0∈A(x,c(x)),进而 0=x⊙c(x)∈F,矛盾!因此 x∈F与c(x)∈F不同是成立.反之,设x∈F与c(x)∈F不同是成立,如果0∈F,则由F为上集得x∈F且c(x)∈F,矛盾!

命题2.1 设(X,→,0)为PFI代数,则X的任一真MP滤子都可延拓为一个极大MP滤子.

证明 设F为X的任一真MP滤子,为叙述方便,记包含F的全体真MP滤子之集为Con(F),则(Con(F),奂)是一个非空偏序集.设 L 是(Con(F),奂)中任意链,则由注2.1(1)知L必有上确界,从而由Zorn引理可知(Con(F),奂)必有极大元.则可断言每个极大元F*都是满足F奂F*的极大MP滤子.若不然,存在MP滤子E使得F*奂E但F*≠E且E≠X,于是F奂F*奂E 且 E≠X.这与 F*为(Con(F),奂)的极大元矛盾!因此命题得证.

定义2.51[14]设(X,→,0)是FI代数且覫≠A奂X.称X的包含A的最小MP滤子为由集合A生成的MP滤子,记为.

3 局部PFI代数

定义3.1 设(X,→,0)是一个PFI代数且x∈X.称满足xm=0的最小正整数m为元素x的阶,记为ord(x).如果这样的正整数m不存在,则称x的阶是无限的,即ord(x)=∞.

定义 3.2 设(X,→,0)是FI代数,如果X有唯一的极大MP滤子,则称(X,→,0)是局部的.

设(X,→,0)是 PFI代数，定义 D(X)={x∈X|坌n∈Z+,xn>0}.

显然x∈D(X)当且仅当ord(x)=∞.

命题3.1 设(X,→,0)是一个PFI代数且F是X的真MP滤子,则F奂D(X).

证明 设F是X的真MP滤子.如果x∈F,则坌n∈Z+,由F对⊙封闭可得xn∈F.因为0埸F,所以xn≠0,故 xn>0,即 x∈D(X).因此 F奂D(X).

命题3.2 设(X,→,0)是一个PFI代数,则下列个条件等价

(1)D(X)是X的MP滤子;

(2)坌x,y∈X,坌n∈Z+, 若 xn≠0 且 yn≠0, 则 xnyn≠0;

证明 (1)圯(2):设(1)成立且 x,y∈X.则坌n∈+,若 xn≠0 且 yn≠0,则 x∈D(X)且 y∈D(X),又 D(X)是X的MP滤子,所以x⊙y∈D(X).进而由引理2.2(7)和⊙的交换性可得xn⊙yn=(x⊙y)n∈D(X),因此xn⊙yn>0,即 xn⊙yn≠0.

(2)圯(1):由 D(X)的定义显然有 1∈D(X).坌x,y∈X,设 x∈D(X)且 x→y∈D(X),坌n∈Z+,xn>0 且(x→y)n>0,于是由(2)可知 0≠xn⊙(x→y)n=(x⊙(x→y))n,因此(x⊙(x→y))n>0.又因为由引理 2.2(1)知 y≥x⊙(x→y),所以再由引理 2.2(6)和(7)便得 yn≥(x⊙(→y))n>0,故y∈D(X),从而D(X)是X的MP滤子.

定理3.1(局部PFI代数的特征) 设(X,→,0)是一个PFI代数,则下列各条件等价

(1)D(X)是X的MP滤子;

(2)是X的真MP滤子;

(3)D(X)是X的唯一极大MP滤子;

(4)X是局部PFI代数.

证明 (1)圯(2):设(1)成立,则显然有=D(X).而由D(X)的定义又知0埸D(X),从而0埸,进而是X的真MP滤子,即(2)成立.

(2)圯(3):设(2)成立,则由命题 3.1 知 奂D(X),又因为 D(X)奂,所以 =D(X),这表明D(X)是X的一个真MP滤子.设E是X的任意极大MP滤子,则由命题3.1知E奂D(X),再由D(X)是X的一个真MP滤子和E的极大性可得E=D(X),因此D(X)是X的唯一极大MP滤子.

(3)圯(4):平凡的.

(4)圯(1):设(4)成立,并令F是X的唯一的极大MP滤子,任取x∈D(X),则<{x}>是X的一个真MP滤子,从而由命题2.1知<{x}>可延拓为X的一个极大MP滤子Fx,于是由F的唯一性便得Fx=F,故x∈F,从而 D(X)奂F.另一方面,由命题 3.1 又有 F奂D(X),因此D(X)=F,所以D(X)是X的MP滤子.

定理3.2(局部正则FI代数的特征) 设(X,→,0)是一个正则FI代数,则下列各条件等价

(1)X是局部的;

(2)坌x∈X,ord(x)=∞ 或 ord(c(x))=∞.

证明 (1)圯(2):设X是局部,则由定理3.1知D(X)是X的MP滤子.如果存在x∈X使得坌n∈Z+都有 xn>0 且(x(x))n>0,则由命题 3.2 知 xn⊙(c(x))n≠0,但由引理 2.2(8)又有(x⊙c(x))n=0,矛盾!因此坌x∈X,ord(x)=∞ 或 ord(c(x))=∞,即(2)成立.

(2)圯(1):设(2)成立.显然 1∈D(X).如果 x∈D(X)且x→y∈D(X),则由X的正则性可得c(x→c(y))=x→y∈D(X),故存在 m∈Z+使 ord(x⊙c(y))=m,即

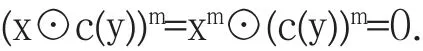
因此(c(y))m≤c(xm).由 x∈D(X)知,坌n∈Z+,xn>0,从而必有坌k∈Z+,(xm)k=xmk>0,故xm∈D(X).于是ord(c(xm))=l<∞,即(c(xm))l=0,故

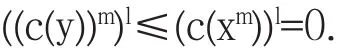
所以(c(y))ml=(xm)l=0,即 ord(c(y))≤∞,故 ord(y)=∞,即 y∈D(x).因此 D(X)是 X 的 MP 滤子,所以由定理3.1知X是局部的.

〔1〕王国俊.数理逻辑引论与归结原理(第二版)[M].北京:科学出版社,2006.

〔2〕Chang C C.Algebras Analysis of Many-valued Logics[J].Trans.Amer,Math.Soc.,1958,88:467-490.

〔3〕Belluce L P,Nola A D,Lettieri A.Local MV-algebras[J].Rend.Circ.Math.Palermo,,1993,42:347-361.

〔4〕Turunen E,Sessa S.LocalBL-algebras[J].Mult.Val.Logic,2001,6(1-2):229-250.

〔5〕刘练珍,李开泰.局部 R0代数[J].数学研究与评论,2005,25(3):538-542.

〔6〕吴望名.Fuzzy蕴涵代数 [J].模糊系统与数学，1990,4(1):56—64.

〔7〕王国俊.MV代数,BL代数,R0代数与多值逻辑[J].模糊系统与数学,2002,15(3):1-15.

〔8〕Xu Y,Ruan D,Qin K Y,Liu J.Lattice-Valued Logic[M].Berlin:Springer,2003.

〔9〕李志伟,郑崇友.HEYTING代数与FUZZY蕴涵代数[J].数学杂志,2002,35(2):237-240.

〔10〕朱怡权,曹喜望.关于 PFI代数与剩余格[J].数学进展,2006,35(2):223-231.

〔11〕刘春辉,吴红霞,徐罗山.关于 CFI代数[J].扬州大学学报(自然科学版),2007,10(4):1-4,8.

〔12〕刘春辉,徐罗山.赋范 Fuzzy蕴涵代数[J].扬州大学学报(自然科学版),2009,12(3):1-5.

〔13〕刘春辉.正则Fuzzy蕴涵代数的理想格[J].内蒙古师范大学学报(自然科学汉文版),2009,38(1):4-8.

〔14〕刘春辉,徐罗山.Fuzzy蕴涵代数的MP滤子[J].模糊系统与数学,2009,23(2):1-6.

〔15〕刘春辉,徐罗山.Fuzzy蕴涵代数的素MP滤子[J].模糊系统与数学,2011（1）.

O141.1；O153.1

A

1673-260X（2011）11-0014-03