负相协样本下总体分位数的经验似然渐近性质的推断
李乃医,李永明
(1.广东海洋大学理学院,广东湛江524088;2.上饶师范学院数学与计算机学院,江西上饶334001)
负相协样本下总体分位数的经验似然渐近性质的推断
李乃医,李永明
(1.广东海洋大学理学院,广东湛江524088;2.上饶师范学院数学与计算机学院,江西上饶334001)
文章在强平稳负相协样本下,利用分组经验似然比方法,克服了传统经验似然方法的缺陷,所得到的渐近分布为标准的卡方分布,便于构造总体分位数的渐近置信区间。
强平稳;负相协;分组经验似然;置信区间
0 引言
NA(Negative Associate)相依概念在可靠性理论、渗透理论和多元统计分析中有广泛的应用。经验似然是1988年最早由Owen[7][8]引入经验似然,它是一种非参数推断方法,类似于Bootstrap和随机加权方法,但有所不同的是它在每个样本点上所赋予的概率是带有选择余地的,在一些合理的约束条件下,描绘了支撑在样本上的一个多元似然,而经验似然比方法所构造置信区域就是此多元似然的一个等高区域。更值得一提的是经验似然比置信区域具有保范围性,它与被置信的总体特征具有同样的范围,这是其它方法所不能到达的。并且它的区域形状完全由样本决定,其覆盖概率不比Bootstrap置信区域差。正是由于经验似然与经典或现代的其它统计方法相比具有上述突出的优点。因此,该方法引起了国内外许多统计学家的兴趣,并将这一方法应用到多种统计模型及各种领域。
在相依情形下,经验似然方法研究刚刚开始,尤其在NA相依样本下利用该方法研究成果甚少。到目前为止,在独立样本和混合样本下对分位数进行了经验似然方法研究。本文将尝试在NA(负相协)相依样本下,克服普通经验似然方法的缺陷,重新借助分组经验似然比方法,构造未知的分位数渐近置信区间。首先给出NA序列和强平稳概念。
定义1[1]称随机变量X1,X2,…,Xn(n≥2)是NA的,如果对于集合{1,2,…,n}的任何两个不相交的非空子集A1和A2,都有
Cov(f1(Xi,i∈A1),f2(Xj,j∈A2))≤0
其中f1与f2是任何两个使得协方差存在的对每个变量均非降(或非升)的函数。称随机变量序列{Xi,i∈N}是NA序列,如果对任何n≥2,随机变量X1,X2,…,Xn(n≥2)都是NA(负相协)的。
定义2 随机变量序列{Xn|n≥1}称强平稳,若对任意自然数对(i,j),序列(Xi+1,…,Xi+j)与(X1,…,Xj)有相同分布,其中1≤j 对数经验似然比为 这里s∈R1且满足 条件: (1)X1,X2,…,Xn是强平稳NA样本; 定理1若上述条件成立,则有 此处 由于A2和σ2未知,结果不便应用,为了弥补这一缺陷,利用分组经验似然方法,重新构造经验似然比以使其极限分布不含未知参数。 (注:关于条件(2)是研究NA序列,通常需要对协方差结构做出这一约束要求。) 定理2在定理1的条件下,进一步有以下假设成立: (2)Y2i-1=ξi/m,Y2i=ηi/m(1≤i≤g)。 其中 则有 其中λ∈R1,满足 分组后经验似然比R'(ξp)由下式决定 本文以下为了简单起见,适当抽样使n=2mg。文中常数c在不同的地方可以取不同的值。 引理1[9]设{Xn,n≥1}为NA序列;A1,A2,…,Am是集合{1,2,…,n}的两两不交的非空子集。记αi=#(Ai),即为Ai中的元素个数,如果fi:Rαi→R(i=1,2,…,m)是对每个变元都非降(或非升)的函数,则f1(Xj,j∈A1),…,fm(Xj,j∈Am)仍为NA变量。 引理3[3]设X1,X2,…,Xn为NA变量,对p≥2,有E|Xj|<∞,且EXj=0,j=1,…,n。记则存在仅与p有关的常数Cp>0,使得 引理4[2]设{Xi|i≥1}是强平稳NA序列,假定EX1=0,E|并且则有 引理5 设{Xi|i≥1}是强平稳NA序列,并且满足 则有 其中 引理6[10]设{Xn,n∈N}是NA序列,数列{bn,n∈N}满足且则s收敛于0。 引理7 设{Xn,n∈N}是同分布的NA序列,则有 引理8 设{Xi|i≥1}是同分布NA序列,则有 易得 从而可知0是集合{I{X1≤ξp}-p,1≤i≤n}所构成的凸包的内点,因此存在为正。 又因为 由拉格朗日乘子法,得唯一解 其中s∈R1,并满足注意到: 令γi=s(I{Xi≤ξp}-p),s满足h(s)=0,由(6)式及引理2知: 于是有 因此 再由引理4和引理7知: 由条件得J2=Op(1) 又由(6)和引理2得 其中c为某个正数,故有 综合(9)~(11)式便得 类似前面的讨论,只需证明 由拉格朗日乘子法得 其中λ∈R1,且满足易得 从而有 接下证明 又由 利用引理8得 由(18)及(19)式得 又由 由引理5和(18)式得 又由(21)、(22)和(24)式得 由(23)式和Taylor展开式得 利用引理5及引理4,同样讨论得 由(24)式得 由(18)和(24)式得 从而得K3=Op(1),综(25)~(28)式知 定理2结论中的渐近分布不仅为标准的卡方分布,且无需估计总体未知的方差和协方差。 利用定理2,当样本n比较大时,我们可构造未知的分位数ξp的置信水平为1-α的渐近置信区域:1-α,其中Cα为分布的上α分位点,通常α取0.05或 0.01。另外,在其它相依情形,如在正相协样本下,值得进一步深入研究。 [1]Joag-DevK,ProschanF.NegativeAssociationofRandom Variable with Application[J].Ann.Statist.,1983,11. [2]潘建敏.NA序列中心极限定理的收敛速度[J].应用概率统计,1997, 13(2). [3]杨善朝.随机变量部分和的矩不等式[J].中国科学,A辑,2000,30(3). [4]张军舰,王成名等,相依样本情形下经验似然比置信区间[J].高校应用数学学报,1999,(14). [5]Kitamura,Y.Empirical Likelihood Methods with Weakly Dependent Process[J].Ann.Statist.,1997,(25). [6]Lin,L.,Runchu,Z.Block Empirical Edulidean Likelihood for Weakly Dependent Process[J].Statist.Probab.lett,2001,(53). [7]Owen,A.B.Empirical Likelihood Ratio Confidence Intervals for a Single Function[J].Biometrika,1988,(75). [8]Owen,A,B.Empirical Likelihood Confidence Regions[J].Ann. Statist.,1990,(18). [9]Matula,P.A Note on the Almost Sure Convergence of Sum of NegativeDependentRandomVariables[J].Statist.Probab.lett,1992,(15). [10]万成高.NA序列的大数定律及收敛速度[J].湖北大学学报(自然科学版),2004,(3). [11]秦永松,有偏模型中一类统计泛函的经验似然估计及渐进性质[J].应用数学学报,1998,(3). [12]Owen,A.B.Empirical Likelihood for Linear Model[J].Ann.Statist, 1991,(4). [13]秦永松.部分线性模型参数的经验似然比置信区域[J].应用概率统计,1999,(4). [14]Chen,S.X.EmpiricalLikelihoodIntervalsforNonparametric Density Estimation[J].Biometrika,1996,83. [15]Chen,S.X,Qin,Y.S.Coverage Accuracy of Confidence Intervals in Nonparametric Regression[J].Acta Mathematicae Applicate Sinica,English Series,2003,(19). [16]Chen,S.X,Hall,P.Smoothed Empirical Likelihood Confidence for Quantiles[J].Ann.Statist,1993,(21). [17]Chen,S.X,Wong,C M.Smoothed Block Empirical Likelihood for Quantiles of Weakly Dependent Processes[J].Statistica Sinica, 2009,(19). [18]Zhang,J.J.Empirical Likelihood for NA Series[J].Statist.Probab Lett,2006,(76). [19]于卓熙,王德辉,史宁中.NA误差下部分线性模型的经验似然推断[J].系统科学与数学,2009,(4). [20]Zhu,L.X,Xue,L.G.Empirical Likelihood Confidence Regions in a Partially Linear Single-Index Model[J].Journal of the Royal Statistical Society Series B-Statistical Methodology,2006,(68). [21]Xue,L,G,Zhu,L,X.Empirical Likelihood for a Varying Coefficient Model with Longitudinal Data[J].Journal of the American Statistical Association,2007,(102). (责任编辑/亦民) O212.4 A 1002-6487(2011)06-0017-04 国家自然科学基金资助项目(11061029);广东海洋大学自然科学研究资助项目(1012138;0612163) 李乃医(1979-),男,江西九江人,硕士,讲师,研究方向:数理统计。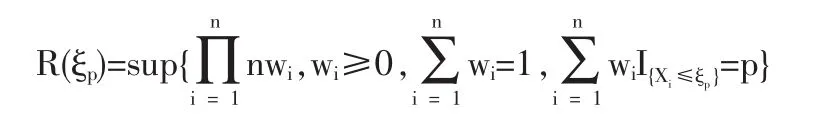
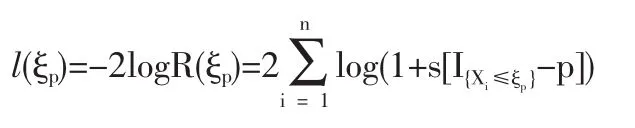
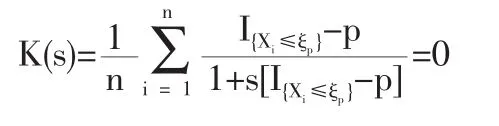
1 若干引理和定理
1.1 定理与引理
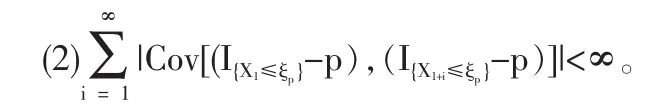
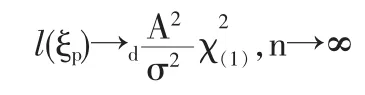
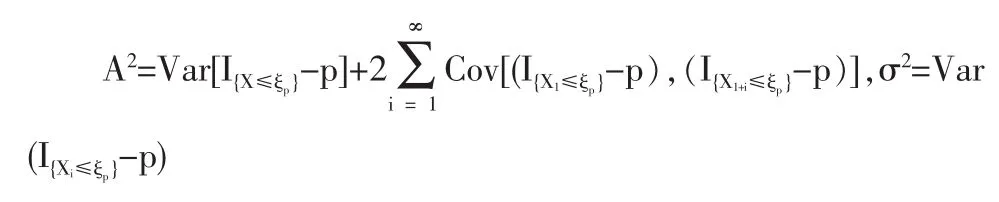
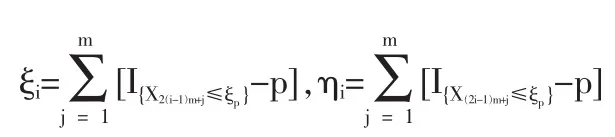
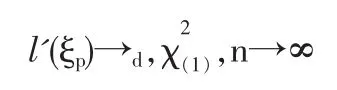
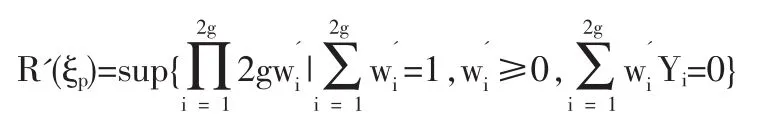
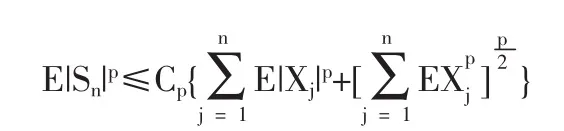

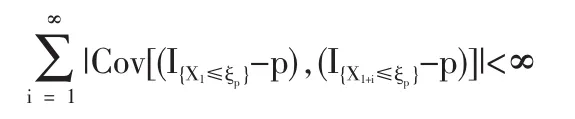
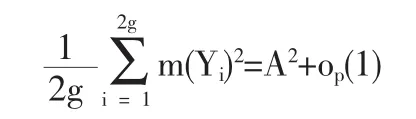
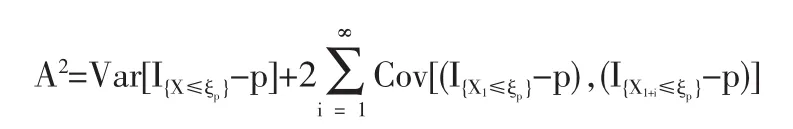
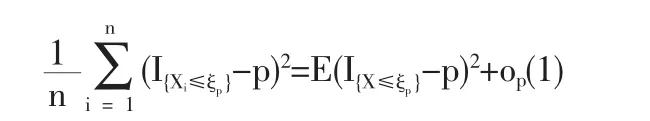
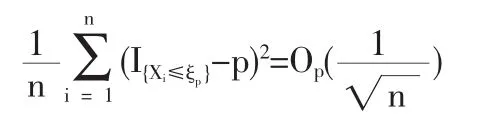
1.2 定理1的证明
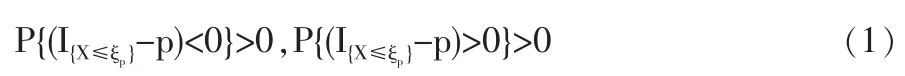

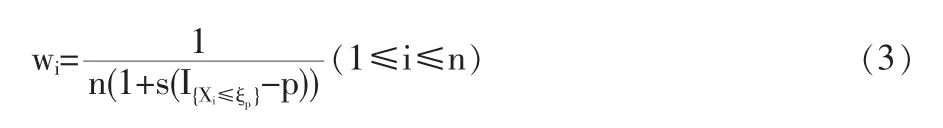
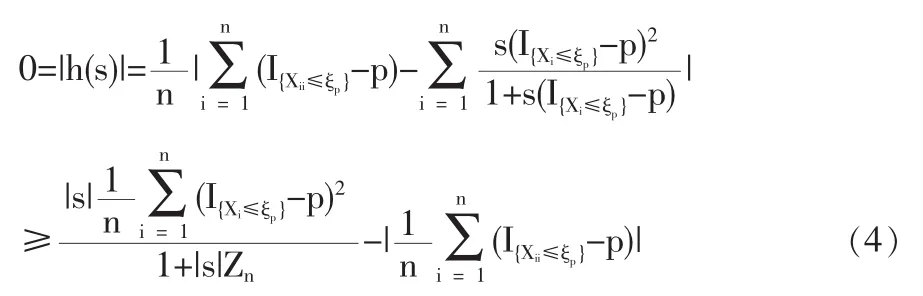

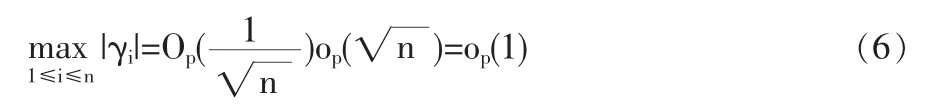
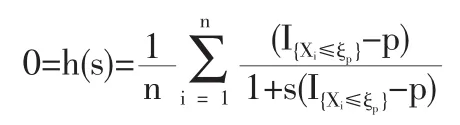
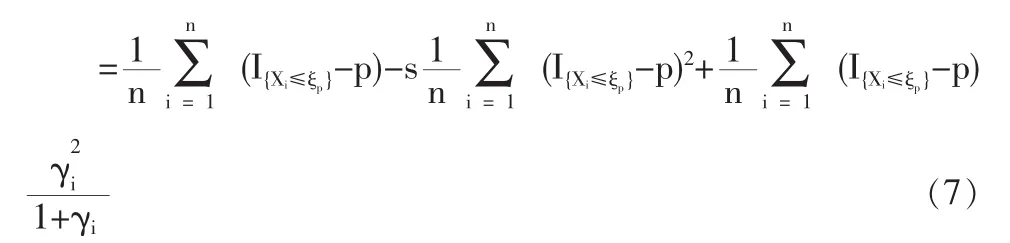
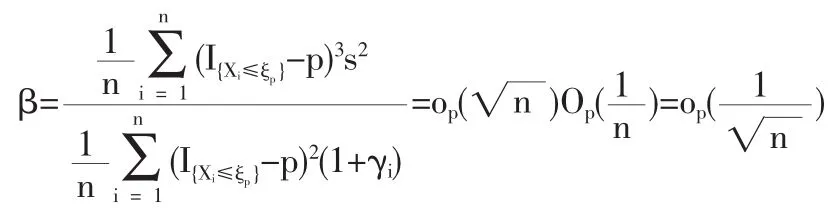
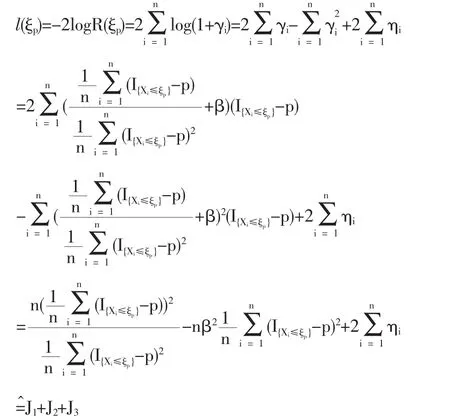

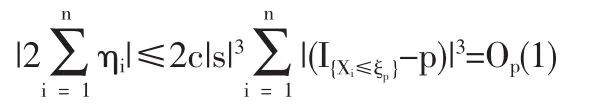


1.3 定理2的证明

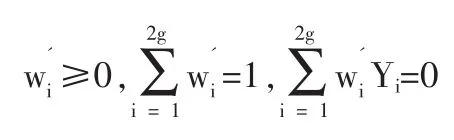
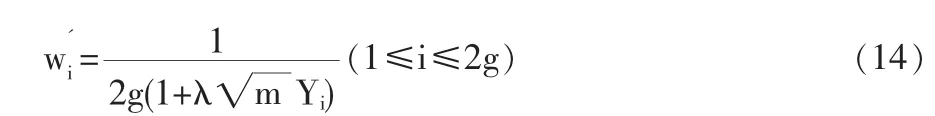
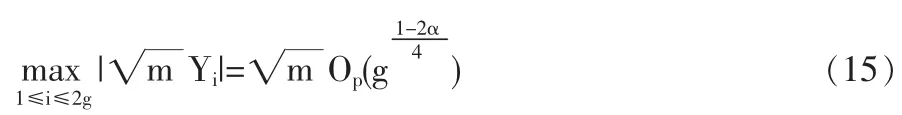
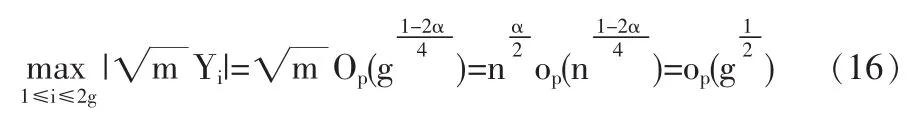

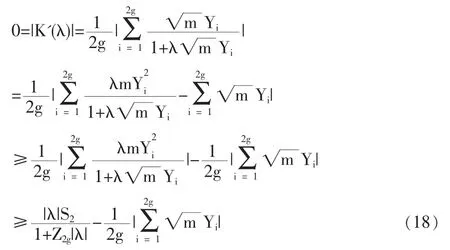
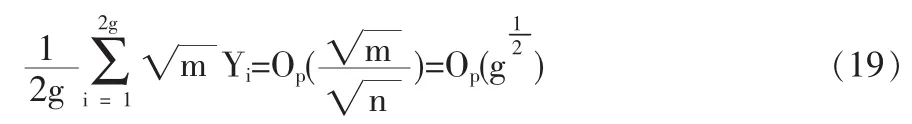

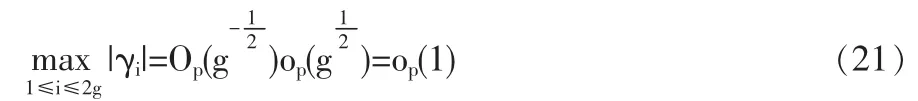
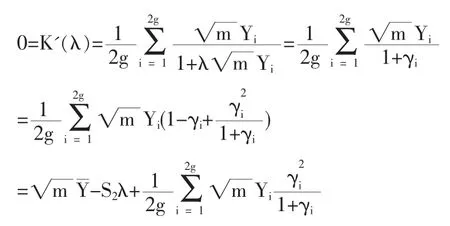

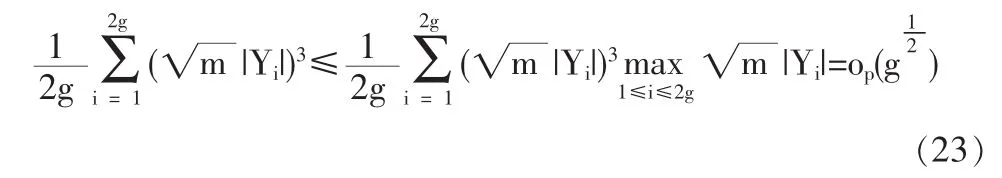
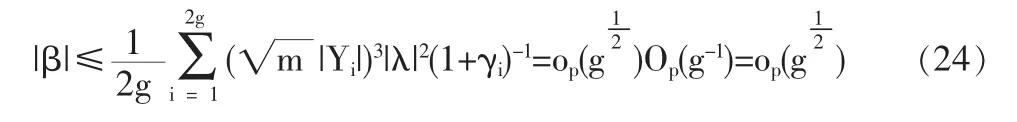
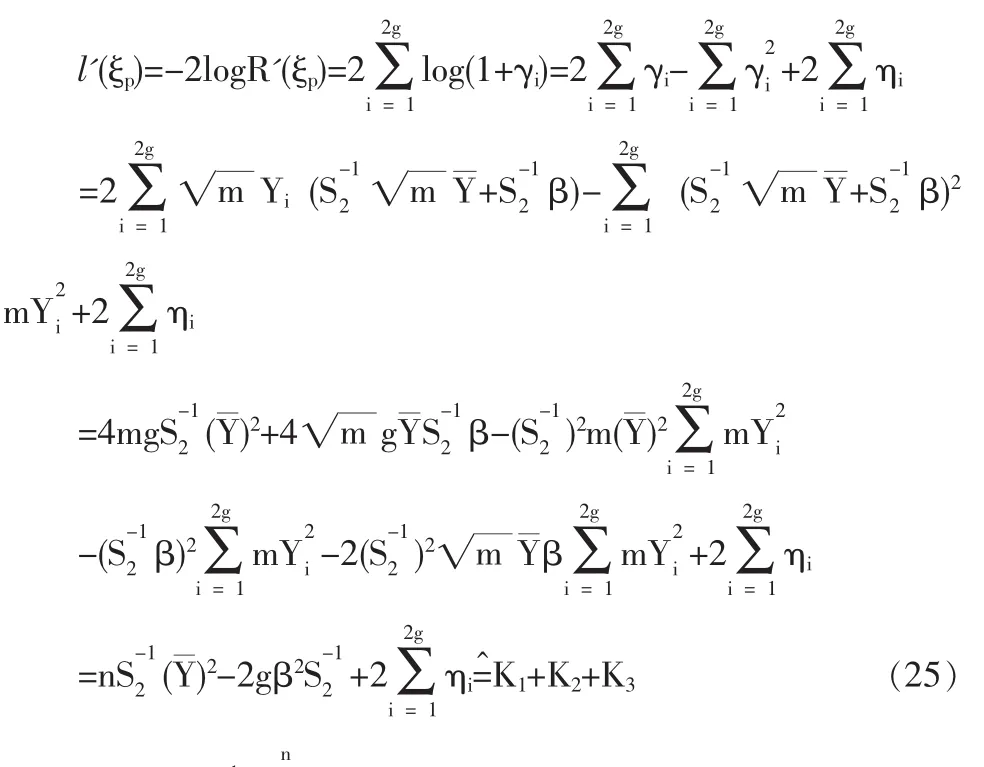


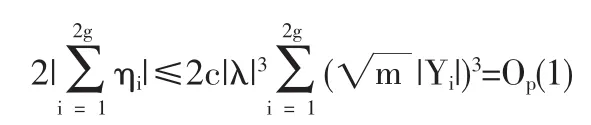

2 结论

