关于t-范数的构造方法
樊东红 曾 彦
(钦州学院 物理和材料学院,广西 钦州 535000)
关于t-范数的构造方法
樊东红 曾 彦
(钦州学院 物理和材料学院,广西 钦州 535000)
文章对t-范数的发展历史和取得的成果进行了论述,并且给出了相关定义,论证了其基本性质,对其构造展开了全面的分析研究,得到了相应的结果。
t-范数,度量空间,模糊集
1 t-范数的研究历程
t-范数(即:三角范数)的历史起源于论文《统计度量》[Menger 1942],而Karl Menger的本意是构造度量空间使得概率分配而不是数用在其中,以便刻画所提问题中的空间二元素间的距离[1]。
t-范数起重要作用的第一个领域就是概率度量空间的理论[2]。Berthold Schweizer 和Abe Sklar在1961年提出了我们今天仍在使用的t-范数理论,Seratnev 在1962年给出的统计度量的重新定义,许多关于t-范数的结果都是在这一发展过程中得出[3]。
关于函数等式领域,(连续的)t-范数理论与结合性等式(它的更一般形式仍未解决)密切相关[4]。最早的起源是Abel的研究,这一方向的研究有更多的结果[5],尤其Ja’nos Acze’l的专著对t-范数的发展有并且仍将有深远的影响[6],在这个背景下的主要结果是借助加法生成元完全刻画连续的Archimedeant-范数[6]。
研究的另一个方向是为解决一些(或多或少的)自然函数等式的t-范数参数族的证明,关于这一点,最重要的结果多半是Frank 的工作[8],它表明Frank t-范数和t-对偶范数(加上序数和定理)是所谓的Frank函数等式的唯一解决办法。
总之,只需从三种t-范数,即MT ,PT ,LT 借助同构转化和序数和就可以构造出所有的连续t-范数[6]。
2 基本概念
定义2.1三角范数T(简称t-范数)是定义在单位区间[0,1]上的二元运算。即:对函数T: [0 ,1 ]2→ [0 ,1 ] , 使得对所有x,y,z∈ [ 0,1],有以下四个公理成立:
(T1) T(x ,y ) = T (y ,x ) (交换律)
(T2) T(x ,T (y ,z ) ) = T (T(x ,y ),z ) (结合律)
(T3) T(x ,y) ≤ T(x ,z),只要y≤z (单调性)
(T4) T(x , 1 ) = x (边界条件)
例2.1 以下是四种基本的t-范数 TM, TP, TL, TD.
TM(x ,y ) = m in(x ,y)
TP(x ,y ) =x⋅y
TL(x ,y ) = m ax(x + y −1,0)

只有 TL和 TD的结合律是不完全平凡的.因为 TL可以看作:
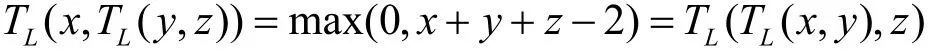
对于 TD只有在 ,y,z 中至少有2个等于1时我们在每一侧上都得到一个不等于0的值,在这种 情况下我们显然在每一侧上都有min(x ,y,z ),这四种基本t-范数很重要。定义 2.2 i)若对 t-范数,不等式对所有的 ( x ,y )∈ [ 0,1 ]2成立,我们就说 T1弱于 T2,或 T2强于 T1,写作T1≤T2。
ii)若T1≤T2且T1≠T2,则说T1< T2.即若 T1≤T2且对某个
从以上两点连同t-范数的性质,我们可以得到如下的包含四种基本的t-范数的比较,总体上说来, 要比较两个t-范数的强弱不是很容易。
注: (i)由(1.3)可知,对每个t-范数T 和每个 ( x ,y )∈ [ 0,1 ]2,有 T (x ,y) ≤ T ( 1, y )= y,T (x,y ) ≤ T (x, 1 ) = x所有的t-范数在
[0,1 ]2的边界上是重合的且对所有的 ( x ,y )∈ ( 0,1 )2,有 T (x ,y ) ≥ 0 = TD(x ,y )。因此, TD是最弱的 t-范数, TM是最强的
t-范数:

(ii)因为显然 TL< TP,所以我们可以得到四种基本t-范数的序:

很显然对 t-范数T最重要的事就是在开单位平方 (0 ,1 )2上满足交换律(T 1 ),结合律(T 2 ), 单调性(T 3 ),然而这不足以保证在整个单位平方 [0 ,1 ]2上的单调性。S:[ 0,1 ]2→ [0 ,1], 使得对所有 x ,y,z∈ [ 0,1 ] ,满足(T1)-(T3)和边界条件

例2.2 以下是四种基本的t-对偶范数 SM, SP, SL,SD。

事实上t-对偶范数的原始定义与以下给出的定义完全等价:
函数S:[ 0,1 ]2→ [0 ,1]是t-对偶范数当且仅当存在t-范数T使得对所有 ( x ,y)∈[0,1]2

3 重要性质
性质3.1 i)从定义2.1我们可以直接推出,对于所有的 x ∈ [ 0,1 ] ,t-范数T满足以下另外的两个边界条件:

因此,所有的t-范数在单位平方 [0 ,1 ]2的边界上都是重合的。
ii) t-范数T在第二个分量上的单调性由(T3)可描述,加之(T1),等价于在两个分支里的(联合)单调性,即:

确实,若 x1≤x2,y1≤y2,则我们有

性质3.2 设A是满足(0 , 1)⊆ A⊆[0,1]的集合,假设*:A2→A 是定义在A上的二元运算,且对所有的x,y,z∈A,满足性质(T1)−(T3)和

则函数T:[ 0,1 ]2→ [0 ,1 ] 是t-范数,其中T定义为:

而且T是唯一的限制到 ( A {1})2与*限制到 ( A {1})2重合的t-范数。
性质3.3 i)对所有的 x ∈ [ 0,1]满足 T (x ,x ) = x的唯一的t-范数是 TM。
ii)对所有的x∈[0,1]满足T(x,x )= 0 的唯一的t-范数是 TD。
4 T-范数的构造
定理4.1:对于 x, y∈[0,1],h∈[-1,1]是x,y的相关系数,则

是T范数。
证明:易得T(ha,b)∈[0,1]。以下验证(1)式满足T-范数的四个条件。由于TP,TM,TL是T-范数,因此边界条件,交换律和单调性显然满足,只需要证明结合律,即证明:

考虑相关参数均属于[0,1]d的情况,则有


上变化,只要能证明P,Q的交集非空,就可以选择合适的参数 h3,h4使得(11)成立。
令

同理可证明 Pmax≥ Qmin,因此P,Q的交集必定非空,因此总能找到适当的参数使交换律满足,同理可证得相关参数为其他情况是时也满足定理,故定理得证。
这里 h是a,b的相关系数,当h=1时,表示a,b间具有最大相关性: Th= TM,当h=0,表明a,b间具有独立相关性,Th= TP;当h=-1,表明a,b间具具有最小相关性, Th= TL当 h在[0,1]间连续变化时, Th将在 TP和 TM间作连续变化,当h在[-1,0]间连续变化时, Th将在 TP和 TL间连续变化。
上述定理即给出了一种T-范数的构造方法。
[1]E. P. klement, R.Mesiar, E. Pap.Triangular-Norms[M].Dordrecht :Kluwer-AcademicPublisher,2000.
[2]E.P.klement,R.Mesiar,E.Pap.Problems on triangular norms and related Operators[J].Fuzzy Sets and Systems,2004,145(3):471-479.
[3]B. Schweizer, A.Sklar. Probabilistic Metric Spaces[M].North-Holland,NewYork,1983.
[4]Funda Karacal.An answers to an open problem on triangular norms[J].Fuzzy Sets and Systems,2005,155(3):459-463.
[5]M. Hosszu.Some functional equations related with the associativity law[M].Publ. Math Debrecen,1954.
[6]C.M.Ling.Representation of associative functions[M].Debrecen:Pub.Math.1965.
[7]J Aczél. Lectures on functional equations and their applications[M].New York:Academic Press,1966.
[8]J. Frank.On the simultaneous associatively of F(x, y) and x+y-F(x, y)[J].A Equations Mathematical,1979,19(2-3):194-226.
CONSTRUCTION AND PROPERTIES OF T-NORM
FAN Dong-hong, ZENG Yan
( Qinzhou University, Qinzhou 535000,China)
In this paper, the history and the results of t-norm are discussed. It gives the related definitions and discusses the basic properties of t-norm. It has a comprehensive analysis of the construction of t-norm. The corresponding results have been
.
t-norm; Metric space; Fuzzy sets
O159
A
1673-2219(2011)08-0032-04
2011-05-03
广西自然科学基金资助项目(2011GXNSFA018151),广西教育厅科研资助项目(201012MS194)。作者简介:樊东红(1964-),女,广西忻城人,钦州学院副教授,主要研究方向为模糊系统及应用。
(责任编校:刘志壮)
——特级教师周卫东《乘法交换律》教学赏析
——特级教师周卫东苏教版四下《乘法交换律》教学赏析

