环Zpα上的重根负循环码

席红旗， 郑喜英， 孔 波

(1.河南教育学院 信息技术系 河南 郑州 450046; 2.黄河科技学院 信息工程学院 数理部 河南 郑州 450005; 3.河南教育学院 数学系 河南 郑州 450046)

0 引言

有限域上的负循环码是Berlekamp[1]提出的，Wolfmann[2]研究了有限环Z4上的奇长的负循环码和单根负循环码，随后Dinh和López-Permouth[3]又将其推广到了有限链环上.目前特征为p的长为n的负循环码(p|n)(称为重根负循环码)成了研究的热点， Blackford[4]研究了Z4上长度为偶数的重根负循环码,并用变换的方法给出了他们的分类,Dinh[5-6]研究了Galois环GR(2a,m)上长为2s的负循环码，并给出了Z2a上长为2s的负循环码的Hamming距离、lee距离和Euclidean距离.Slalgean[7]研究了有限链环上的重根循环码及重根负循环码，证明了有限链环上的重根循环码一般情况下不是主理想生成的,GR(2a,m)上偶长的负循环码是主理想生成的.开晓山[8]研究了Z2a上任意偶长的负循环码, 并给出了Z2a上长为2k的负循环码的Hamming距离和齐次距离.郑喜英[9]研究了有限链环上的重根循环码，给出了其上任一循环码的生成情况.罗维[10]给出了Galois环GR(pm,n)上长为pk循环码的生成情况.本文研究了Zpa[x]上的重根负循环码的生成情况.

1 有限链环上的多项式环及其理想

r=r0+er1+…+ek-1rk-1,ri∈S,i=0,1,…,k-1.

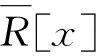
2 环Zpα上的重根负循环码

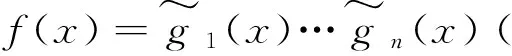
定理2令F为特征为p的域(p非零且为素数),n=pβl且p不能整除l.(i) 若l为奇数，则xn+1=(x+1)pβp1(xpβ)…pr(xpβ)，其中(x+1)pβ,p1(xpβ), …,pr(xpβ)是xpβl+1在F[x]中的分解且是互素的.(ii) 若l为偶数，则xn+1=(q1(x))pβ…(qr(x))pβ，(q1(x))pβ…(qr(x))pβ是xpβl+1在F[x]中的分解且(q1(x))pβ,…,(qr(x))pβ是互素的.

证明(i) 若l为奇数，则

xn+1=(xpβ)l+1=(xpβ+1)(xpβ(l-1)-xpβ(l-2)+…-xpβ+1)=(x+1)pβ(xpβ(l-1)-xpβ(l-2)+…-xpβ+1).

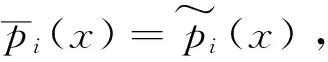
(xpβ)l-1-(xpβ)l-2+…-xpβ+1=p1(xpβ)…pr(xpβ).

因此在Zpα[x]中

xn+1=(xpβ+1)((xpβ)l-1-(xpβ)l-2+…-xpβ+1)=(xpβ+1)p1(xpβ)pr(xpβ).

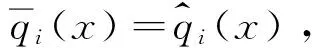
xn+1=(q1(x))pβ…(qr(x))pβ.

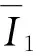
令Z表示整数环,Zc=Z/cZ为模正整数c的整数剩余类环. 令Zc[x]为Zc上的多项式环,Zc[x]/〈xn+1〉表示由xn+1生成的理想〈xn+1〉上的多项式环的剩余类环.Zc[x]/〈xn+1〉的任何理想C都称为有限环Zc上的负循环码.

引理3记m=min{α,pβ}. 则对任意的整数k(1≤k≤m)，存在一个Zpα[x]/(xpβ+1)的理想C可由k个多项式生成但不能由k-1个多项式生成.

证明将文献[9]命题 4.4证明中的(xpβ-1)换成(xpβ+1)可得引理3的证明.

引理4记m=min{α,pβ}. 则对任意的整数k(1≤k≤m)，存在一个Zpα[x]/(qi(x))pβ的理想C可由k个多项式生成但不能由k-1个多项式生成.

证明将文献[9]命题 4.4中的Zpα[x]/(xpβ+1)换成Zpα[x]/(qi(x))pβ,可得引理4的证明.

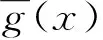
定理3令n=pβl且p不能整除l，m=min{α,pβ},则对任意的整数k(1≤k≤m)，存在一个Zpα[x]/〈xn+1〉的理想C可由k个多项式生成但不能由k-1个多项式生成.

证明(i) 若l为奇数，由定理2可知，在Zpα[x]中xn+1=(xpβ+1)p1(xpβ)pr(xpβ)且xpβ+1,p1(xpβ),…,pr(xpβ)彼此互素. 由中国剩余定理得

Zpα[x]/〈xn+1〉≅Zpα[x]/〈xpβ+1〉⊕Zpα[x]/〈p1(xpβ)〉⊕…⊕Zpα[x]/〈pr(xpβ)〉.

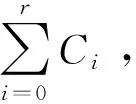
由引理4, 对任意的整数k(1≤k≤m)，存在一个Zpα[x]/〈xpβ+1〉的理想C0=〈pi1gi1(x),…,pikgik(x)〉，可由k个多项式生成但不能由k-1个多项式生成，且由引理5,Zpα[x]/〈pi(xpβ)〉(i=1,…,r)是主理想环,所以根据中国剩余定理, 对任意的整数k(1≤k≤m)，存在一个Zpα[x]/〈xn+1〉的理想C可由k个多项式生成但不能由k-1个多项式生成.

(ii)若l为偶数, 由定理2可知，xn+1=(q1(x))pβ…(qr(x))pβ，且多项式(q1(x))pβ,…,(qr(x))pβ也彼此互素.由中国剩余定理得

Zpα[x]/〈xn+1〉≅Zpα[x]/〈(q1(x))pβ〉⊕…⊕Zpα[x]/〈(qr(x))pβ〉,

参考文献：

[1] Berlekamp E R. Negacyclic codes for the Lee metric[C]//Proc Conf Combinatorial Mathematics and Its Applications. Chapel Hill, NC, 1986: 298-316.

[2] Wolfmann J. Negacyclic and cyclic codes overZ4[J]. IEEE Trans Inform Theory, 1999, 45(7): 2527-2532.

[3] Dinh H Q, Lopez-permauth. Cyclic and negacyclic codes over finite chain rings[J]. IEEE Trans Inform Theory, 2004, 50(8): 1728-1744.

[4] Blackford T. Negacyclic codes overZ4of even length[J]. IEEE Trans Inform Theory, 2003, 49(6): 1417-1424.

[5] Dinh H Q. Negacyclic codes of length 2sover Galois rings[J]. IEEE Tran Inform Theory, 2005, 51(12): 4252-4262.

[6] Dinh H Q. Complete distances of all negacyclic codes of length 2soverZpα[J]. IEEE Trans Inform Theory, 2007, 53(1): 4252-4262.

[7] Ana Sãlãgean. Repeated-root cyclic and negacyclic codes over finite chain rings[J]. Discrete Applied Mathematics, 2006, 154(2): 413-419.

[8] 开晓山.Zpα上的重根负循环码[D]. 合肥: 合肥工业大学, 2007.

[9] 郑喜英.无限长序列及有限链环上的循环码[D]. 武汉：华中师范大学, 2007.

[10] 罗维.Galois环GR(pm,n)上长为pk循环码的注记[J]. 四川师范大学学报:自然科学版，2011，48(11)：45-47.

[11] McDonald B R. Finite Rings with Identity[M]. New York: Marcel Dekker, 1974.