具有化学趋化的双稳增长型核方程的稳定性分析*
蒋名超,刘 萍
(哈尔滨师范大学)
0 引言
近年来,化学趋化问题成为了人们感兴趣的一个研究课题,1950年Patlakh和1970年的Keller、Segel所发表的文章[1]都是我们研究化学趋化问题的基础.Horstmann在他的文章[2]中对Keller-Segel模型进行了细致的分析.基于对化学趋化作用在生物体中影响的了解将化学趋化项加入到数学模型中,并研究带有化学趋化项后对数学模型的一些结构的影响,通过研究数学模型中解的结构及其随着时间的变化等性质有利于进一步了解生物体的发展变化.
1 预备知识
从哺乳动物到微生物,确定食物来源的准确位置,避免遇到捕食者以及吸引异性等都是必要的本领.细胞和有机物朝着化学梯度方向的运动称之为化学趋化.例如蚂蚁向葡萄糖多的地方聚集就是典型的化学趋化作用.化学趋化在数学中广泛应用于物质因受化学物质刺激而产生的运动,这种刺激既包括吸引又包括排斥.化学趋化不仅能够影响物质的分布而且会影响其增长,有时甚至可以作为一个物种与其他具有少的或多的化学趋化影响的物种间竞争有限资源的绝对优势.基于化学趋化对生物体的影响,在数学模型中讨论化学趋化项对方程的影响是很重要的.
令u(x,t)和v(x,t)分别表示在位置x时刻t时由于受到化学趋化的作用物质的密度及物质的集中,假设化学物质是扩散的,则由Fick定律,自由扩散流量可表示为-D2Δv,其中D2为大于零的任意常数;假设细胞的流通与自由扩散流通和化学趋化流通均有关,所以细胞的流量可表示为,其中 χ为常数,D1为大于零的常数,φ'(u)>0,D2是细胞的自动力,测量着细胞自由扩散的能力,χ叫做化学趋化系数,测量着细胞受化学物质影响的大小,当起到吸引作用时χ为正的,当起到排斥作用时χ为负的,φ(u)叫敏感函数,在化学趋化项中我们需要用φ'(u)去反应在不同化学程度下细胞敏感程度的大小.所以一般情况下的带有化学趋化项的数学模型有如下形式:

这是最基本的带有化学趋化项的偏微分方程,随着知识的积累以及对生物体的进一步了解与研究,在Keller-Segel模型的基础上,很多数学家将带有化学趋化项的数学模型进行了广泛的推广,这里我们研究如下模型:
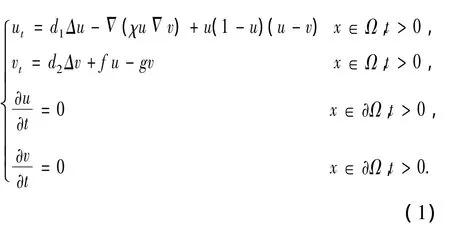
其中 d1,d2,χ,f,g 均为正常数,v∈[0,)
1 预备知识
引理1[3]非线性平面系统的形式为:

一个平衡解(x0,y0)∈ R2满足 f(x0,y0)=0和g(x0,y0)=0.该系统在(x0,y0)的线性化方程为=J·Y,这里J是Jacobian矩阵:

若 F=(f,g):R2→ R2是连续可微的,(x0,y0)是一个平衡点,T,D是Jacobian矩阵J(x0,y0)的迹和行列式.对于系统的平衡点;
(1)当D<0时,平衡点为鞍点;
(2)当D>0且T<0(>0)时,平衡点为稳定结点或螺旋(不稳定结点或螺旋);
(3)若T,D满足其他条件,稳定性无法由J决定.
2 主要结论
2.1 建立方程组求平衡解

2.2 平衡解的稳定性
系统(1)相应线性系统的Jacobian矩阵为:

则:
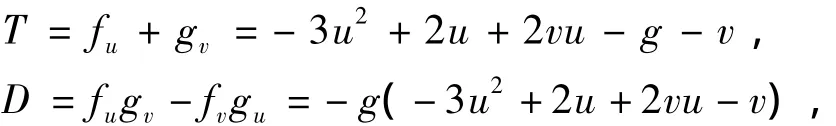
其中T为矩阵J(u,v)的迹,D为矩阵J(u,v)的行列式.那么特征值方程为:

对于这三个平衡解我们有以下结论:
(1)平衡解(0,0):

此时迹T=-v-g<0,行列式D=vg>0,特征值方程有两个负特征值 -v,-g,所以(0,0)为(2)的局部稳定的常数平衡解.

此时迹T=-1+v-g<0,行列式D=(1-v)g>0,特征值方程有两个负特征值-1+v,-g,所以()为(2)的局部稳定的常数平衡解.

此时行列式D=-(-v2+v)g,当时,-v2+v>0,所以D<0,特征值方程有一个负特征值,一个正特征值,所以为(2)的局部稳定的常数平衡解.其相图如图1所示:
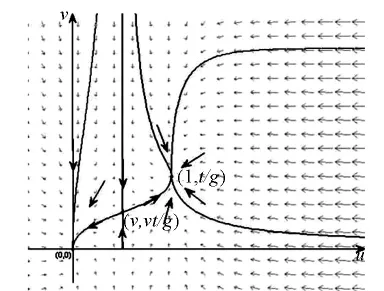
图1
[1] Keller E F,Segel L A.Initiation of slime mold aggregation viewed as an instability.J TheorBiol,1970,26:399-415.
[2] Dirk Horstmann,From 1970 until now:The Keller-Segel model in chemotaxis and its consequences I and II.Jahresber.2003,105(2):51-69.
[3] 丁同仁,李承治.常微分教程.北京:高等教育出版社,2008.

