基于粘合的思想研究整和图

石端银,　张秋杰,　李文宇

(黑龙江科技学院 理学院, 哈尔滨 150027)



基于粘合的思想研究整和图

石端银,张秋杰,李文宇

(黑龙江科技学院 理学院, 哈尔滨 150027)

为了以数据的形式来存储图，引入了整和图标号理论。采用顺序标号法提供了联图和花树的一种整和标号，从而进一步利用粘合的思想方法证明了有公共顶点的一系列多重联图和多重花树仍然是整和图。该研究推广了整和图类型，进一步完善了整和图理论。

整和图； 粘合； 花树； 联图

0　引　言

文中所研究的图都是有限且无方向的简单图,所采用的表示符号及专业术语都与文献[1]相同。为了更好的研究图的理论,早在1988年Harary提出了和图概念[2],令图G=(V,E),其中,V表示图的顶点集,E表示图的边集,设φ是由图G的顶点集V到自然数集N的一个标号函数,它满足:边v1v2∈E当且仅当φ(v1)+φ(v2)=φ(v3),其中v1,v2,v3∈V,则称该图为和图。由定义可以看出和图都是非连通的,一定存在孤立点。如果图G是连通图,则它一定有非零和数。图G的和数σ(G)为使得图G变为和图所添加的最少孤立点的和数。后来,Harary又推广了和图的理论,从而导出整和图的概念,若图G的顶点可以用一个关于不同整数的标号函数λ给出,使得v1v2∈E当且仅当λ(v1)+λ(v2)=λ(v3),其中v1,v2,v3∈V,则图G称为整和图(Integral sum graph);整和图有的是连通图,有的是非连通图,这与和图不太相同。例如:阶为n的道路Pn;n≠4的圈Cn;n≠3的轮图Wn等都是整和图;另外,多重龙虾树也是整和图[3]。如果连通图不是整和图,可以求出相应的整和数;图G的整和数是指使图G成为整和图所需添加孤立点的最少个数。关于整和图理论更详尽的内容可参考文献[4-5]。

粘合的思想最早是由Chen Zhibo在1998年提出来的,利用这种思想可以使得一系列整和图的证明变得更为简便。受粘合的思想的启发,笔者利用顺序标号法研究了由一个公共顶点的多重联图以及多重花树是整合性。

1　基本概念

定义1[6]两个图G1=(V1,E1)和G2=(V2,E2),假设点r1∈V1是G1的一个固定结点,称其为G1的根,r2∈V2是G2的根,令(G,r)=(G1,r1)∞(G2,r2)表示图G的根为r,且点r是由r1和r2粘合而得到的,若不强调r是图G的根,则可以简记G=(G1,r1)∞(G2,r2);其中∞就是粘合符号;显然G的顶点集V=(V1-{r1})∪(V2-{r2})∪{r},G的边集E=E1∪E2。

定义2设两个图G1=(V1,E1)和G2=(V2,E2)不相交,在G1∪G2中,把G1中的每个顶点和G2中的每个顶点连接起来得到的图称为G1和G2的联图。

2　联图的整和性

引理1[8]令(Gi,ri)是带有根ri且存在一整和标号φi(i=1,2)的图,假设:

(1)∀x∈V(Gi)-{ri},φi(x)≠0,i=1,2;

(2)φ1(x)=φ2(y)当且仅当x=r1,y=r2;

(3)对于所有不同的a,b∈V(G1),且x∈V(G2)-{r2},有φ1(a)±φ2(b)≠φ2(x);

(4)对于所有不同的x,y∈V(G2)且a∈V(G1)-{r1},有φ2(x)±φ2(y)≠φ1(a);

则G=(G1,r1)∞(G2,r2)是整和图。

定理1联图G=P1∨Pn是整和图,其中P1=a0,Pn=a1a2…an是道路。

证明下面给出G的一个整和标号l,使得l(a0)=0,l(a1)=1,l(a2)=-1,l(ai)=l(ai-2)-l(ai-1)(i≥2)。显然G=P1∨Pn是整和图。

定理2联图G1=P1∨Pn1,G2=P1∨Pn2;按照定理1中的标号,则G1∞G2是整和图。

直接由引理1和定理2便可得到推论1。

推论1G1=P1∨Pn1,G2=P1∨Pn2,…,Gm=P1∨Pnm,则G1∞G2∞…∞Gm是整和图。

3　花树Tn，F是整和图

定理3所有的花树Tn,F都是整和图。

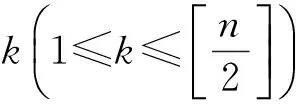
证明(1)当V(Tn,F)≤4时,显然花树Tn,F都是整和图;

(2)当V(Tn,F)≥5时,采取标号:

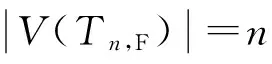
按照定理3中的标号方式,分别对图1中的T24,F和T23,F进行顺序标号如图2所示。

则(G,r)=(G1,r1)∞(G2,r2)是整和图。

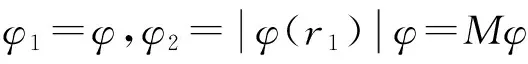
(1)对∀x∈V(G1)-{r1},有φ1(x)≠0;对∀x∈V(G2)-{r2},有φ2(x)≠0;

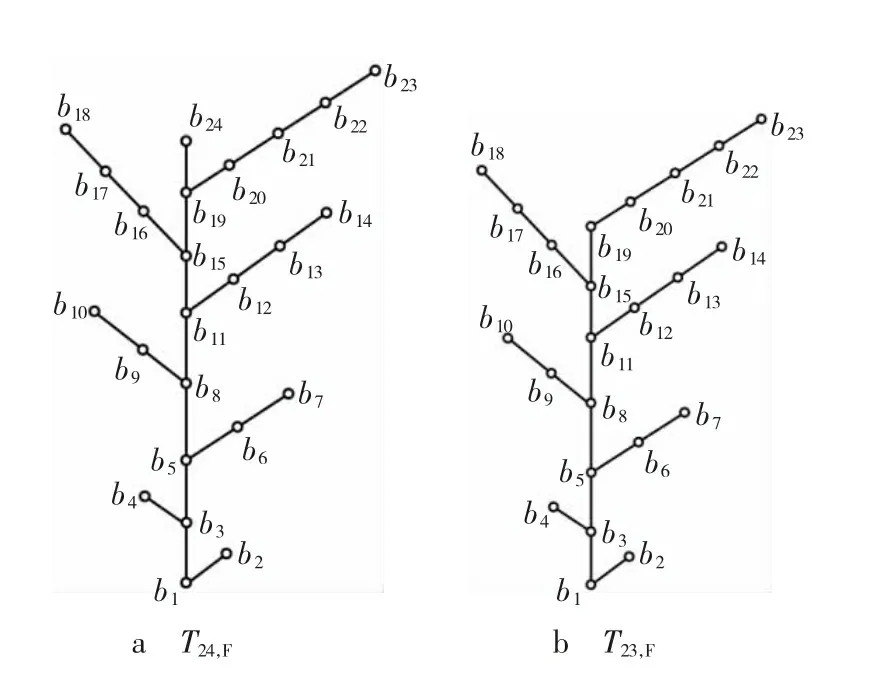
图1　两类花树

图2　花树T24,F和T23,F的整和标号

(4)∀ai,aj∈V(G1),则

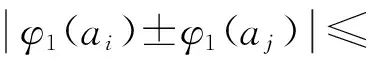
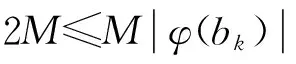
对∀bk∈V(G2)-{r2};由引理1知:(G,r)=(G1,r1)∞(G2,r2)是整和图。

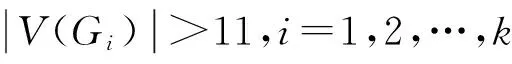
4　结束语

以和图的理论为基础,利用顺序标号法为联图和一般花树分别提供了一类整和标号,证明了联图和花树的整和性质。基于粘合思想方法,证明了由有限个具有一个公共顶点的多重联图及多重花树都是整和图。该结论推广了整和图类型,完善了整和图标号理论,也为研究其他优美图的整和性质提供了一定的理论基础。

[1]WANG HAIYING. The sum numbers and the integral sum numbers of the graphKn+1E(K1,r)[J]. Discrete Mathematics, 2010, 309(12): 4137-4143.

[2]HARARY F. Sum graphs over all the integers[J]. Discrete Mathematics, 1994, 124(1/3): 99-105.

[3]石端银, 徐晶, 丛凌博. 用粘合的方法研究一类新的整和图[J]. 黑龙江科技学院学报, 2010, 20(5): 403-405.

[4]FERNAU H, RYAN J F, SUGENG K A. A sum labeling for the generalised friendship graph[J]. Discrete Mathematics, 2008, 308(5/6): 734-740.

[5]PYATKIN A V.Subdivided trees are integral sum graphs[J]. Discrete Mathematics, 2008, 308(9): 1749-1750.

[6]CHEN ZHIBO. On integral sum graph[J]. Discrete Mathematics, 2008, 306(1): 19-25.

[7]马克杰. 优美图[M]. 北京: 北京大学出版社, 1991.

[8]CHEN ZHIBO. Integral sum graph from identification[J]. Discrete Mathematics, 1998, 181(1): 77-90.

(编辑王冬)

Research on integral sum graph based on identification

SHIDuanyin，ZHANGQiujie，LIWenyu

(College of Sciences, Heilongjiang Institute of Science & Technology, Harbin 150027, China)

This paper introduces the theory of integral sum graph labeling in order to store the graph in the form of data. The paper provides the integral sum labeling of joined graphs and flower trees adopting order labeling method and proves that all multiple joined graphs and all multiple flower trees with the same vertex remain integral sum graphs using the idea of identification. This study fascitates a wider use of the type of integral sum graph and an improvement in the integral sum graph theory.

integral sum graph; identification; flower tree; joined graph

1671-0118(2012)06-0645-03

2012-09-11

黑龙江省教育厅科学技术研究项目(12523046)

石端银(1980-),女,山东省菏泽人,讲师,硕士,研究方向:图论,E-mail:shiduanyin@yahoo.com.cn。

O157.5

A