Two-level Bregmanized method for image interpolation with graph regularized sparse coding
Liu Qiegen Zhang Minghui Liang Dong
(1Department of Electronic Information Engineering, Nanchang University, Nanchang 330031, China)(2Paul C. Lauterbur Research Centre for Biomedical Imaging, Shenzhen Institutes of Advanced Technology, Chinese Academy of Sciences, Shenzhen 518055, China)
Image interpolation is a fundamental and widely studied problem in image processing. It aims to recover a plausible image from incomplete data (e.g., pixels sampled at a subset region). Since this problem is ill-posed, incorporating some prior knowledge into the recovery is needed. The conventional image interpolation algorithms mostly exploit the local correlation of image pixels. For example, B-spline interpolation[1]employed cubic splines to fit the local intensity/regression function; and the kernel regression (KR) framework used adaptive local covariance structures to locally guide the linear or higher order regression for interpolation[2]. Zhang et al.[3]presented a local coherent autoregressive (AR) model, which assumed that the underlying image is piecewise stationary. Motivated by recent progress in local intrinsic manifold assumption, Liu et al.[4]developed a graph-Laplacian regularized local linear regression method (RLLR), which used the geometric structure of the marginal probability distribution as an additional local smoothness-preserving constraint.
Some algorithms based on nonlocal and similarity priors have attracted much attention in the past few years. For instance, the success of the patch-based nonlocal method (PN) depends on iteratively projecting onto two convex sets: one is given by the observation data and the other is defined by the sparsity-based nonlocal prior BM3D[5]. Dong et al.[6]combined the promising sparse representation and nonlocal auto-regression model for interpolation.
More recently, the combinations of local and nonlocal priors have received an increasing amount of interest. Zheng et al.[7]presented a graph regularized sparse coding (GraphSC) algorithm, which introduces ak-nearest neighbor graph into the sparse coding objective function as a regularizer for image classification. In this paper, we propose a two-level Bregmanized method with graph regularized sparse coding (TBGSC). The GraphSC prior is incorporated into a two-level Bregmanized iterative procedure to achieve better recovery ability and computation efficiency for image interpolation.
1 Preliminary
1.1 Bregman iterative method and augmented Lagrangian scheme
The augmented Lagrangian (AL) method is a promising technique and used in various image recovery problems[8-9]. Consider the following optimization problem with linear equality constraint:

(1)
It can be solved by the standard AL method; i.e. the solution of Eq.(1) is achieved by solving a sequence of unconstrained subproblems, in which the objective function is formed by adding the additional “penalty” terms to the objective function of the original constrained optimization. The “penalty” terms are made up of constrained functions multiplied by a positive coefficient.
(2)
(3)
Eq.(3) is often called the Bregman iterative method[10-11].
The relationship of the AL method and the Bregman iterative method was discussed in Ref.[10]. They are identical when the constraint is linear[8,11]. As explained in Refs.[10-11], the iterative procedure (3) has interesting multi-scale interpretation.
1.2 Graph regularized sparse coding
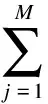
(4)
In short, the objective function of GraphSC consists of three terms: the empirical loss function, the Laplacian regularizer, and the L1-based sparse penalty function:
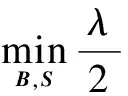
(5)
2 TBGSC Algorithm
In this section, the TBGSC algorithm for image interpolation is derived. We useuto represent the image to be reconstructed andfrepresents the observation data. These two variables are related asFpu=f, whereFprepresents the partially sampled encoding matrix. Undersampling occurs when the number of samples is less than the number of image entries.
2.1 Outer-level Bregman iterative method
When considering the GraphSC as a regularizer, image recovery can be reformulated as follows:

(6)
By applying the Bregman iteration, the solution of Eq. (6) can be obtained by iteratively solving an unconstrained problem and then modifying the value offused in the next iteration. It yields
(7)
A merit of the Bregman iteration is that the residual ‖Fpuk+1-f‖2of the sequence generated by Eq.(7) converges to zeros monotonically.
2.2 Inner-level Bregman iterative method
DenotingX=Ruand employing operator splitting to the subproblem in Eq.(7), the unconstrained minimization problem is transformed to an equivalent constrained problem:
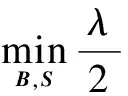
(8)
The augmented Lagrangian function of problem (8) is
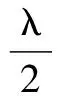
(9)
Since it is difficult to directly find the saddle point of the augmented Lagrangian functionL(B,S,Z,Y), the alternating direction method is used to solve the following sub-problems individually and alternatively.
2.2.1 S- and Z-subproblems
First, the minimization of Eq.(9) with respect toZcan be analytically computed andZcan be eliminated. Specially, from the first and the forth terms of Eq.(9), we obtain the optimal solution:

(10)
Moreover, it follows that

(11)
Secondly, substitutingZof Eq.(10) into Eq.(9), it yields
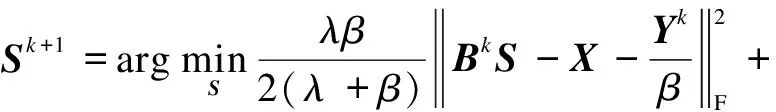
(12)
Note that when updatingsi, the other vectors {sj}j≠iare fixed. Thus, after some mathematical manipulation, we obtain the optimization problem for eachsi:
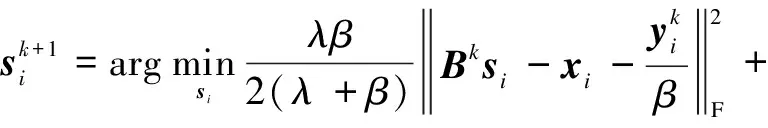
(13)
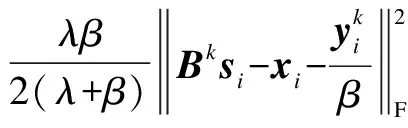

(14)
2.2.2 B-subproblem
We can obtain the rule of updating gradient descent by taking the derivative of Eq.(9) with respect toB:
Bk+1=Bk-ζ[-Yk+β(BkSk+1-Zk+1)](Sk+1)T=
Bk+ζYk+1(Sk+1)T
(15)
A normalization of dictionary columns is required after the gradient descent.
2.2.3 u-subproblem
In order to achieve faster convergence speed, the variableuis updated at each inner iteration of the Bregman iterative process, which yields
(16)
The least squares solution satisfies the normal equation,
(17)
and yields
(18)
In summary, the proposed Bregmanized method consists of a two-level nested loop. The outer loop updates the variablefk+1, while the inner loop alternatively updates the variablesB,S,Z, andu.
3 Experimental Results
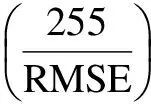
Figs.1 and 2 show that the TBGSC produces the most visually pleasant results especially for those images with complex texture, indicating better recovery ability under higher undersampling ratios. The iterative property of the proposed TBGSC for recovering image “barb2” withrof 15% is illustrated in Figs.3 and 4. Fig.3 displays the PSNR value vs. iterations, where the Bregman iteration-based dictionary learning approach demonstrates a notable ability to increase the PSNR value quickly. Fig.4 depicts the sequence of intermediate recovered image and corresp-onding dictionaries at the 2nd, 5th, 8th, 15th iterations. It can be observed that from the first to the fifth iterations most of the edge objective atoms are constructed and furthermore from the eighth to fifteenth iterations more and more details are added to the atoms. Additionally, the average computation time per iteration is about 4.19s. Here, our method was implemented in Matlab 7.10.0 on a PC equipped with AMD 2.31 GHz CPU and 3 GB RAM.
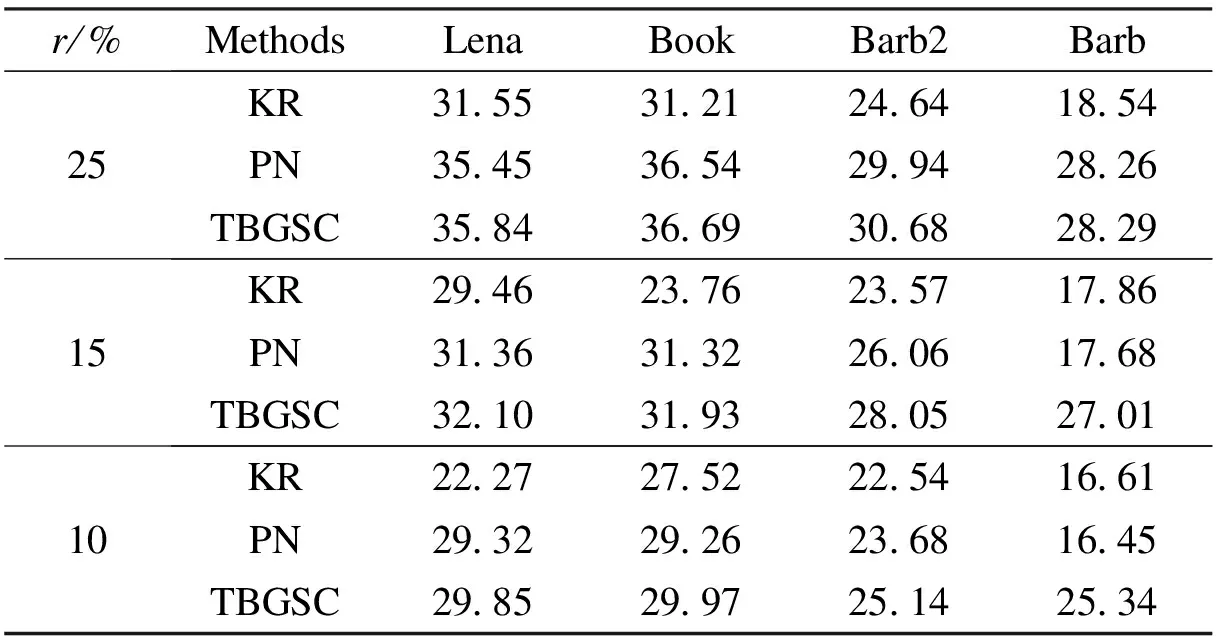
Tab.1 PSNR results of three methods under different sampling ratios

Fig.1 Subjective comparison on four toy-example images with r of 15%. (a) Reference image; (b) Observation; (c) KR; (d) PN; (e) TBGSC

Fig.2 Subjective comparison on two toy-example images with r of 10%. (a) Reference image; (b) Observation; (c) KR; (d) PN; (e) TBGSC

Fig.4 Intermediate recovered images (top line) and the corresponding dictionaries (bottom line) generated by TBGSC after iterations with r of 15%. (a) After 2nd iteration; (b) After 5th iteration; (c) After 8th iteration; (d) After 15th iteration
In Fig.5, the comparison on two generic images “house” and “Lena” is conducted, wherer=15% is maintained. The recovery PSNR of KR, PN and TBGSC for “house” are 29.39, 30.96 and 31.75 dB, and for “Lena” are 26.08, 26.45 and 27.13 dB, respectively. Fig.5 shows the enlargements of the reconstruction results. Since the proposed method utilizes both the local and nonlocal priors, the image local structure can be better recovered by the TBGSC as observed in Fig.5. Besides, although PN also aims to exploit the non-local redundancies existing in the image, it may fail and generate some artifacts.It is probably because not many nonlocal redundancies around those structures can be recognized when the observations are highly undersampled. In contrast, our method can overcome this shortcoming by posing the local constraint on the coefficients.

Fig.5 Subjective comparison on images “house” and “Lena” with r of 15%. (a) Reference image; (b) KR; (c) PN; (d) TBGSC
4 Conclusion
In this paper, we propose a two-level Bregmanized method with graph regularized sparse coding for image interpolation. The nonlocal and local geometrical structure information, exploited by graph regularized sparse coding, is incorporated into the two-level Bregmen iterative procedure. Experimental results show that the proposed algorithm outperforms existing algorithms both in terms of vision and PSNR, particularly under highly undersampled observation.
[1]Hou H S, Andrews H C. Cubic splines for image interpolation and digital filtering [J].IEEETransactionsonAcousticsSpeechandSignalProcessing, 1978,26(6): 508-517.
[2]Takeda H, Farsiu S, Milanfar P. Kernel regression for image processing and reconstruction [J].IEEETransactionsonImageProcessing, 2007,16(2): 349-366.
[3]Zhang X J, Wu X L. Image interpolation by adaptive 2-D autoregressive modeling and soft-decision estimation [J].IEEETransactionsonImageProcessing, 2008,17(6): 887-896.
[4]Liu X M, Zhao D B, Xiong R Q, et al. Image interpolation via regularized local linear regression [J].IEEETransactionsonImageProcessing, 2011,20(12): 3455-3469.
[5]Li X. Patch-based image interpolation: algorithms and applications [C]//InternationalWorkshoponLocalandNon-LocalApproximationinImageProcessing. Lausanne, Switzerland, 2008: 1-6.
[6]Dong W S, Zhang L, Lukac R, et al. Sparse representation based image interpolation with non-local autoregressive modeling [J].IEEETransactionsonImageProcessing, 2013,22(4): 1382-1394.
[7]Zheng M, Bu J J, Chen C, et al. Graph regularized sparse coding for image representation [J].IEEETransactionsonImageProcessing, 2011,20(5): 1327-1336.
[8]Afonso M, Dias J B, Figueiredo M. An augmented Lagrangian approach to the constrained optimization formulation of imaging inverse problems [J].IEEETransactionsonImageProcessing, 2011,20(3): 681-695.
[9]Liu Q G, Wang S S, Luo J H, et al. An augmented Lagrangian approach to general dictionary learning for image denoising [J].JournalofVisualCommunicationandImageRepresentation, 2012,23(5): 753-766.
[10]Yin W T, Osher S, Goldfarb D, et al. Bregman iterative algorithms forl1-minimization with applications to compressed sensing [J].SIAMJournalonImagingSciences, 2008,1(1): 142-168.
[11]Xu J, Osher S. Iterative regularization and nonlinear inverse scale space applied to wavelet-based denoising [J].IEEETransactionsonImageProcessing, 2007,16(2): 534-544.
[12]Dong W S, Li X, Zhang L, et al. Sparsity-based image denoising via dictionary learning and structural clustering [C]//IEEEConferenceonComputerVisionandPatternRecognition. Colorado Springs, CO, USA, 2011: 457-464.
 Journal of Southeast University(English Edition)2013年4期
Journal of Southeast University(English Edition)2013年4期
- Journal of Southeast University(English Edition)的其它文章
- Optimal decision thresholdfor soft decision cooperative spectrum sensing
- Exponential stabilization of distributed parameter switched systems under dwell time constraints
- Direct linear discriminant analysis based on column pivoting QR decomposition and economic SVD
- RBF neural network regression modelbased on fuzzy observations
- Design and analysis of dual-mode structure repetitive control based hybrid current regulation scheme for active power filters
- Aerodynamics of flexible wing in bees’ hovering flight
