用小波矩阵形式改进Daubechieschies小波的正交性
张旭俊
(江西省电力科学研究院,江西南昌 330096)
0 引言
小波理论是20世纪的数学里程碑,Haar小波简单对称,但它不连续、不可微的缺点,数学家不能接受。寻找具有紧支撑、连续、可微的小波十分困难,法国著名数学家Meyer曾企图证明小波正交基(Haar小波除外)并不存在,但最后他提出多分辨小波分析方法,并由数学家Daubechies提出一个正交的小波族,当N=1时它就是Haar小波,N≥2时,就是Daubechies小波族,但两者关于小波正交的理念是完全不同的。经典小波理论是在傅里叶变换的广义积分中表达小波基正交条件的,大篇理论叙述中,迟迟不见小波在时域中的形象,读者理解较难,特别是对离散的等距采样数据的小波分析而言,由于数据长度有限,会发生边缘数据小波分析的失真。本文将用小波矩阵的方法铨明并改造Daubechies小波矩阵的正交性,用小波矩阵分析是从时域中来理解正交性的,不涉及傅里叶广义积分的概念,读者理解要容易得多,从小矩阵导入方法,读者不难用举一反三的推理,扩展到任意阶的大矩阵。
1 用Haar小波矩阵作光滑分解
作者用Haar小波矩阵来分析等距采样数据,为了分析结果的平滑,先依不同尺度进行平均值滤波、数据压缩,再光滑插值重构主体成分的“恢复像”,将“原始信号”减去主体成分的“恢复像”,就得到按时域分布的细节:“总谐波像”,它也是光滑的曲线。这样就基本上解决了对系列数据按“时-频”分析的问题。

由原始采样数据 求出小波系数C如下:

由小波系数C重构原始函数F如下:

以下只以实例说明Haar矩阵按双尺度分解的过程和结果。
设采样数据由式(4)得到f(i),称之为F列向量,采样点数取N=2n=128点,相应的Haar矩阵B是128阶方阵,
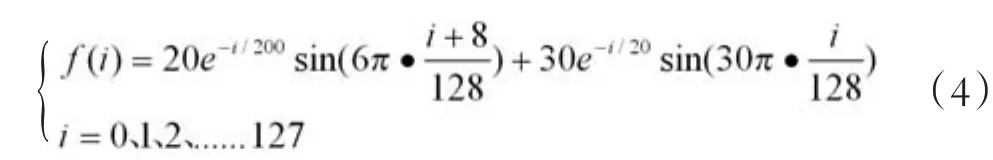
若尺度压缩选择取2m=8倍,即略去m=3层以上的高次小波,于是只需保留B矩阵的上面2n-m=16行的数据,称作BU矩阵,它是16×128阶矩阵,函数重构解出的f1(i)步骤很简单,它无需写出128阶B矩阵作运算,其f1(i)的结果就是从开始,每连续8个点都用它们相应的平均值代替,由此所形成阶梯波的“模糊像”如图1。再将每连续8个相同的数据只保留一个(图1下的小圆圈),得到压缩数据s[k],其中k=0、1、2、…….15,如式(5)
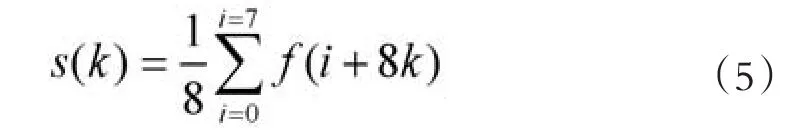

图1 Haar小波矩阵分析的效果
再采用光滑插值的方法,在 和 中间求双抛物线的平均值,从而将这16点压缩数据扩展成128点,就得到主体成分的“恢复像”,再将“原始像”减去“恢复像”得到“总谐波像”,它也是光滑曲线,如图1。这样就得到的“时-频”分解结果。
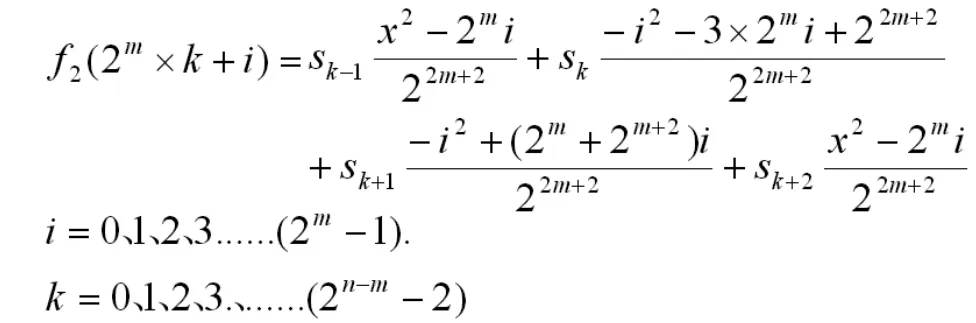
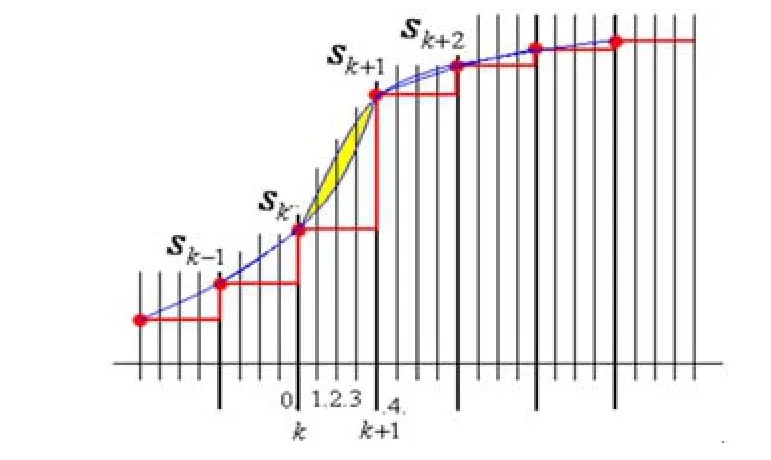
图2 用双抛物线法求平均插值
2 正交子波变换
多尺度表达的离散小波函数

经典小波重构的公式是:

引入双尺度函数和小波函数,及其傅里叶变换函数,如公式(9)、(10),
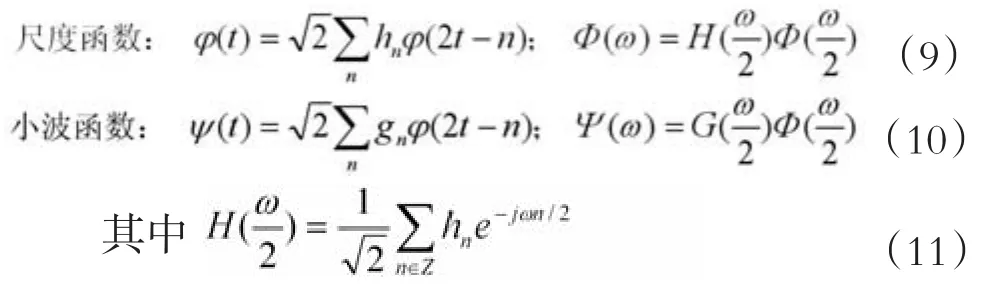
尺度函数和另一平移后的尺度函数应当是正交的,用公式表示如下,

同理也可得到关于小波正交条件的公式(13)

由小波函数和尺度函数的正交关系可有:

3 Daubechies小波族
法国数学家Daubechies提出了一组正交小波的滤波函数 的公式(15):
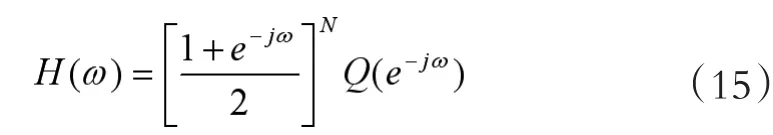
其中 是有关 的(N-1)次多项式。

显然它满足尺度函数的正交条件(12)式。
2)当N=2时Daubechies小波的尺度滤波函数直接写出为:
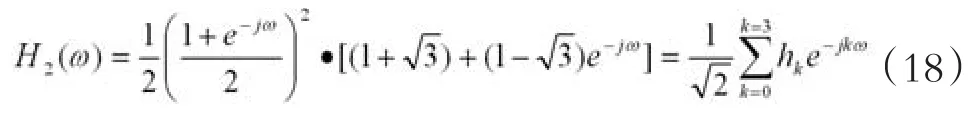
展开后可得其中4个系数是:

相应的4个小波系数为:

一般也简称其为Db4小波,参考资料中对各种N下的Daubechies小波,都具有2N个尺度系数,简称Db(2N).为验证其正交性,改写(18)如下:
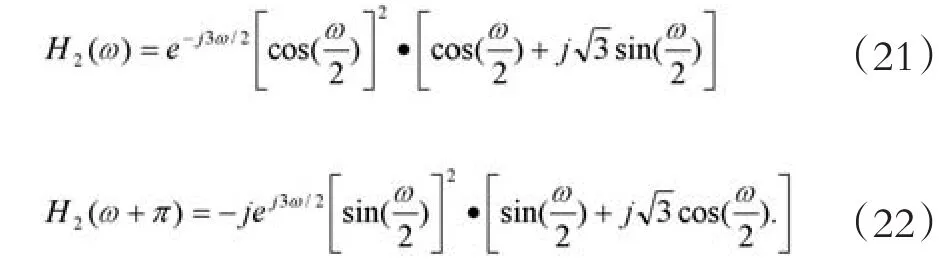
可得:

这种在频域中验证尺度函数的正交性,很难使读者对小波分解有感性认识,而且也见不到小波的形状。
4 Db4小波矩阵
特以N=2时的Daubechies小波为例,简称Db4小波。我们感兴趣的依然是希望能像Haar小波矩阵那样展开,一次性地把各个层次的小波都计算出来,但这是不可能做到的,这就是数学家Meyer曾企图证明小波正交基(Haar小波除外)并不存在。但最后他提出多分辨小波分析方法,就是按尺度和小波系数,一层一层地剥开,逐次显示该层次的小波和尺度的幅值,每剥一层信号点数就应当减半。为描述这个思路还是用8阶矩阵来加以说明。前4行放置尺度波形,后4行放置小波波形,如第1行是4个尺度系数,右边4个零,第5行是4个小波系数,右边4个零。第2、6行是将第1、5行向右移位2列,第3、7行是将第2、6行向右移位2列,第4、8行是将第3、7行向右移位2列,这时出现了截断的现象,有两个列跑出了方矩阵的范围。方矩阵的右边是列向量F,它是原始信号的数据等号右边的列向量X是待求的尺度幅值c和小波幅值d。从几何意义看,尺度波形就是小波波形就是,解这个联立方程就可将原始信号分解为尺度和小波的幅值,

把(24)式简写成(25)式,如果希望按原来尺度和小波的波形重构原函数,就应当如公式(26)那样,但关键是H矩阵是否是正交矩阵,验证如下:

如(27)式所示,H不是正交矩阵,需加以改造,

如果把第4、8行移位时截断的两个列,循环地移到相应行中的第1、2列上,可有(28)式,从物理意义上理解佗相当于原始数据是周期性循环的。

简写为B·F=X……(29),令人兴奋的是B矩阵是正交矩阵,
从而可有波形重构公式(32)


下面以前例128点的采样数据进行Db4矩阵的分解重构工作,先后进行3层剥离,如图3所示。为了对比在图的右边画出用Haar矩阵作光滑分解的对应结果,相当于压缩2、4、8倍,由于Haar矩阵光滑分解采用插值处理,各层的“恢复像”都有128点数据画线,比较光滑,可见用Haar矩阵作光滑分解依然具有使用方便的优势,且它能直接进入某个尺度进行分解。
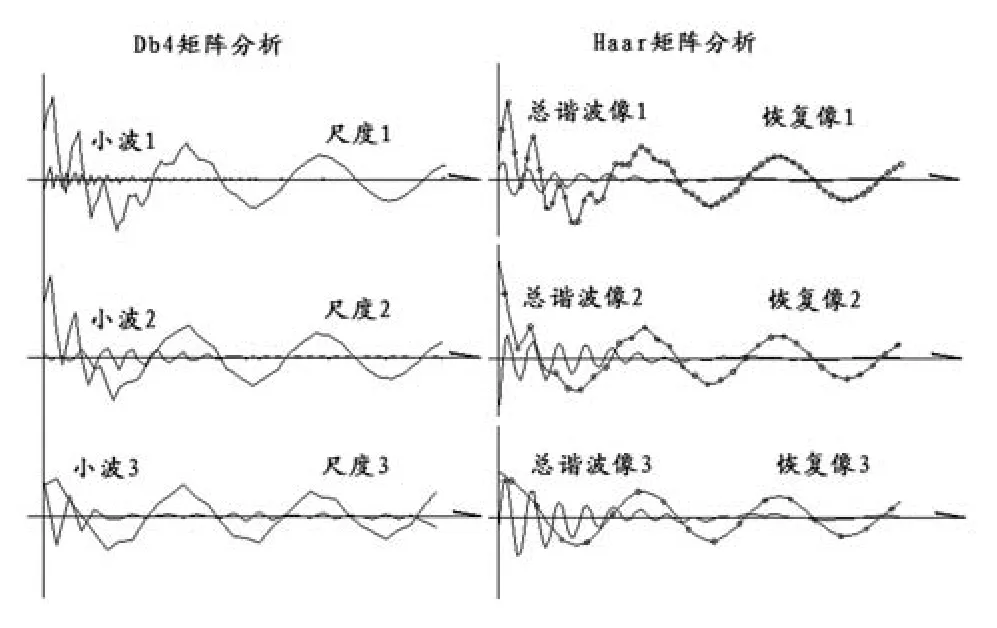
图3 两种小波矩阵分析法结果的对比
5 结论
必须注意Haar矩阵的正交性可以一次性将原始采样点数据分解为:直流、2次、4次、8次……到2n-1次小波,而DB4矩阵的正交性却只能将N=2n点数据分解为:尺度和2n-1次小波,其中尺度就是所有2n-m次小波的总和,(m=2、3、……n),DB4分解虽然不能一次到位,却能接连进行分解。法国著名数学家Meyer曾企图证明小波正交基(Haar小波除外)并不存在,然后他又提出双尺度多分辨小波的分析方法,创造出多层剥离的另一种的正交概念,这也是卓越的创举,本文用小波矩阵的方法把这两者之间的差异明白地表达出来。令人兴奋的是,在离散函数的分析时,Daubechies小波DB4、DB6、…….DB20等都可以按本文的方法构成正交的B矩阵,从而使小波分析的概念完全转到时域中来理解。
如第一节所述,Harr小波矩阵的基小波支撑区是[1,2],没有前后的拖尾,像切香肠一样清晰,它的正交性明确。至于其不连续、不可微的缺点,可通过平均值滤波,数据压缩,光滑插值膨胀,完全得到解决。所以作者特推荐用Harr小波矩阵作光滑分解的方法。
[1]张旭俊.用小波矩阵作小波分析[J].电力系统自动化,1999(24).
[2]张旭俊.小波分解和高次小波差分的奇异点[J].电力自动化设备,2001(2).
[3]张旭俊.用小波矩阵分析法进行函数的分解与重构[J].江西电力,2007(4).
[4]张旭俊.用小波矩阵分析Mallat算法的物理几何含义[J].江西电力,2010(1).
[5]赵松年.子波变换与子波分析[M].北京:电子工业出版社,1996.
[6]程正兴著.小波分析算法与应用,[M].西安西安交通大学出版社,1998.

