指数为1的半正定线性系统迭代方法的收敛性

崔艳星 王川龙

（1.长治学院 数学系，山西 长治046011；2.太原师范学院 数学系，山西 太原030012）

0 引言

奇异的半正定系统有广泛而重要的应用.例如求解具有Neumann边界条件线性弹性方程组，广义有限元方法产生的代数系统，以及Markov chain模型等方面.有很多关于半正定线性系统迭代方法的收敛性的文章，也给出了半正定系统的收敛条件，其中最有影响的是Keller[1]给出的P－正则条件.Keller指出在该条件下线性系统收敛的充要条件是系数矩阵对称半正定.Lee[2]给出了奇异的半正定系统收敛的新条件，并且举例说明P－正则条件或弱正则条件都不是奇异的半正定系统收敛的必要条件.

我们来考虑下面的线性方程组的求解问题

奇异.

一般采用迭代法求解该线性方程组，令A＝M－N，且M可逆.则（1）可以写成如下的等式:

对于上述的固定迭代方法，Keller给出了下面的收敛定理:

定理1[1]A是n阶奇异对称矩阵，A＝M－N是P－正则分裂，则迭代方法（2）收敛到（1）的一个解当且仅当A对称半正定.

A的指数是使得rank（Ak）＝rank（Ak＋1）最小非负整数k，或者是A的零特征值的最大Jordan块的维数.如果M不可逆且index（M）＝1，我们在（2）中用Mg换掉M－1，得到下面的迭代格式:

Mg代表M的群逆（定义2）.

在本文中我们只考虑对称半正定矩阵A的指数是1的情形下迭代格式（3）的收敛性.在第二部分中我们主要介绍群逆，商收敛，半范数收敛的概念.还将介绍半范数收敛，商收敛的简单性质.第三部分主要讨论第二部分提出的几个收敛性之间的关系，以及半范数收敛的一些新结果.第四部分主要学习对称半正定系统的收敛性，以及给出本文的主要结论.

1 基本概念

在本文中，用Rn，Rn×n分别表示n维实向量空间和n阶实矩阵空间，AT，N（A），R（A）分别表示A的转置，A的零空间和A的值域.

定义1[3]169A∈Rn×n，index（A）＝k，则存在X∈Rn×n使得

X称为A的Drazin逆，记为X＝Ad.特别地，如果k＝1，X称为A的群逆，记为X＝Ag.

如果A可逆，则显然index（A）＝0，而且Ad＝A－1.

定义2[5]8设A是n阶对称半正定矩阵，T是n阶矩阵，x∈Rn，令

显然它是向量x的一个半范数，而再令

是矩阵T的一个半范数.

定义3[2]如果迭代格式（3）中‖I－MgA‖A＜1，则迭代格式（3）称为半范数收敛.

如果index（A）＝1，则P＝AgA是R（A）上的斜投影，x＊＊＝Agb是指数为1的相容线性系统的一个解，而且x＊＊＝Agb是唯一的最小S－范数解[6].

定义4[6]已知index（A）＝1，设P＝AgA，如果对于∀x∈Rn由迭代格式（3）产生的迭代序列｛Pxk｝收敛到解x＊＊＝Agb，（k→∞）.那么迭代格式（3）称为商收敛.

2 几个收敛性之间的关系

我们来讨论半范数收敛与收敛的关系，为了说明他们的关系我们先来介绍下面的引理以及推论.

引理1[7]如果index（M）＝1，那么迭代格式（3）收敛与商收敛等价.

推论1[7]迭代格式（3）收敛当且仅当

下面的两个定理使我们这部分的主要结果.

定理2 已知A半正定，如果迭代格式（3）半范数收敛，那么它一定收敛.

证明 设x＊＊＝Agb，则迭代格式（3）可改写为:

其中T＝I－MgA.

如果‖T‖A＜1，那么有下面的等式成立:

迭代格式（3）的半范数收敛可以得到下面有用的性质:

定理3 已知A半正定，如果迭代格式（3）半范数收敛，那么有下面的等式成立:

证明 首先证明第二个等式，显然N（MgA）⊆N（MMgA），而如果MMgAx＝0，等式两边同时乘以Mg，那么得到MgAx＝0，所以N（MgA）⊇N（MMgA），所以有:

下面证明第一个等式，假设N（A）≠N（MgA），而N（A）⊆N（MgA），一定存在x0≠0，使得Ax0≠0，而MgAx0＝0，这就使得，这与迭代格式（3）半范数收敛矛盾，所以有:

证毕.

显然，MMgA＝A是等式（7）成立的充分条件.

3 半范数收敛的新条件

在这一部分中我们讨论对称半正定相容线性系统的半范数收敛性的等价条件，即迭代格式（3）的半范数收敛的充要条件.

定理4[8]A是n阶对称正半定矩阵，则迭代格式（2）半范数收敛当且仅当M＋MT－A在R（M－1A）正定.

在文献[2]中举出一个精致的例子，说明条件P－正则分裂[1]，以及弱－正则条件[4]都不是（3）收敛的必要条件，这就促使我们寻找异于P－正则分裂的条件.

定理5 如果A半正定，且MMgA＝A成立，M＋MT－A在R（MgA）上对称正定当且仅当:

成立.

证明

从（9）式易知MgAx≠0时，（（M＋MT＋A）MgAx，MgAx）＞0当且仅当（8）成立.

定理5中的条件显然比定理1中的P－正则条件弱，如果M可逆，那么MMgA＝A总是成立的，那么定理的条件就退化为定理4中的P－正则条件.

定理6 如果A半正定，且MgA＝A成立，则迭代格式（3）的半范数收敛当且仅当M＋MT－A在R（MgA）上对称正定当且仅当（8）成立.

证明

所以迭代格式（3）的半范数收敛当且仅当M＋MT－A在R（MgA）上对称正定或等价的（8）成立.

定理7MMgA＝A成立当且仅当R（A）⊂R（M）成立当且仅当N（MT）⊂N（A）成立.

证明 后一个等价条件显然成立.

设MMgA＝A，则（Mg）TMT＝A，所以N（MT）⊂N（A）成立.

反过来，由于MMgM＝M，而R（A）⊂R（M），所以MMgy＝y，y∈R（A）⊂R（M），即:MgA＝A，证毕.

最后我们举一个条件MMgA＝A满足，但是（8）不满足的例子.

例 令

给出A的一个分裂A＝M－N，其中

则经过计算:

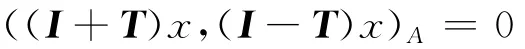
条件（8）不满足，而TTAT＝A，所以迭代不是半范数收敛的.

对于正定系统各种迭代格式收敛性的研究有很多经典的结果，但是对于半正定系统的收敛会相对复杂一些.比如对于迭代格式（3）是否有更加简洁的关于半范数的等价条件，以及多分裂算法[8]的半范数收敛性，都值得进一步学习.

[1]Keller H B.On the solution of singular and semidefinite linear systems by iteration[J].Journal of the Society for Industrial and Applied Mathematics:1965，2（2）:281－290

[2]Lee Youngju，Wu Jinbiao，Xu Jinchao，et al.On the convergence of iterative methods for semidefinite linear systems[J].SIAM J.Matrix Anal，2006，28:634－641

[3]Ben Israel A，Greville T N E.Generalized Inverses:Theory and Applications[M].New York:Wiley，1974

[4]Richard S Varge.Matrix Iterative Analysis[M].2nd.Heidelberg:Edition.Springer，2000

[5]Wei Yimin.Perturbation analysis of singular linear systems with index one[J].International Journal of Computer Mathematics，2000，74（4）:483－491

[6]Cui Xiaoke，Wei Yimin，Zhang Naimin.Quotient convergence and multisp－litting methods for solving singular linear equations[J].Calcolo，2007，44（4）:21－31

[7]Lin Lijing，Wei Yimin，Zhang Naimin.Convergence and quotient convergence of iterative methods for solving singular linear equations with index one[J].Linear Algebra and its Applications，2009，430（5－6）:1 665－1 674

[8]Cao Zhihao.A Note onP－Regular splitting of Hermitian matrix[J].SIAM.J.Matrix Anal.Appl.，2000，21:1 392－1 393