浅谈概率论中“数学期望”概念的讲解

曹小玲

（长江大学 信息与数学学院，湖北 荆州 434023）

浅谈概率论中“数学期望”概念的讲解

曹小玲

（长江大学 信息与数学学院，湖北 荆州 434023）

在概率论与数理统计的学习中，“数学期望”是一个比较抽象的概念，本文阐述了“数学期望”概念讲解中比较重要的三个内容，即：如何“定义”，如何“引申”到连续型随机变量的定义，以及如何“过渡”到方差。

数学期望；概率论与数理统计；教学

在我们进行概率论与数理统计的教学中，教材的编排往往是在进行了随机变量及其分布函数的学习之后，立刻进入随机变量数字特征的学习，而最先面对的数字特征就是数学期望。“数学期望”这个概念的起源源于下面这个经典典故。

早些时候，法国有两个大数学家，一个叫做布莱士·帕斯卡，一个叫做费马。帕斯卡认识两个赌徒，这两个赌徒向他提出了一个问题。他们说，他俩下赌金之后，约定谁先赢满5局，谁就获得全部赌金。赌了半天，A赢了4局，B赢了3局，时间很晚了，他们都不想再赌下去了。那么，这个钱应该怎么分？是不是把钱分成7份，赢了4局的就拿4份，赢了3局的就拿3份呢？或者，因为最早说的是满5局，而谁也没达到，所以就一人分一半呢？这两种分法都不对。正确的答案是：赢了4局的拿这个钱的3/4，赢了3局的拿这个钱的1/4。这是为什么呢？假定他们俩再赌一局，A有1/2的可能赢得他的第5局，B有1/2的可能赢得他的第4局。若是A赢满了5局，钱应该全归他；若B赢得他的第4局，则下一局中A、B赢得他们各自的第5局的可能性都是1/2。所以，如果必须赢满5局的话，A赢得所有钱的可能为1/2+1/2× 1/2=3/4，当然，B就应该得1/4了。数学期望由此而来。

通过这几年的教学体会和教学经验，笔者发现“数学期望”这一概念尽管来源于生活，而且跟现实生活结合得非常紧密，但因为它非常抽象，一般同学学到这个地方就会感觉到难于理解和接受。本文对数学期望概念的讲解进行了介绍，以期起到“抛砖引玉”的作用。

一、关于如何定义“数学期望”

首先是如何引入的问题。对于如何引入“数学期望”，我们为了唤起学生的学习兴趣，激发他们的学习动力，可以举一些密切联系生活的例子，比如上面的经典典故，或者将上面的经典典故作稍许变动，得到另外一个例子，如文献[3]中就是将“赌金问题”换成了“乒乓球比赛问题”。我们也可以作这样类似的变动，以吸引学生的课堂注意力，加深他们对《概率论与数理统计》这门课程在解决生活实际问题的作用是非常大的印象，唤起他们对这门课程的兴趣，也激发他们对用数学方法处理现实问题的热情。

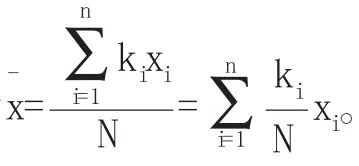
这种引入方法的特点是直接、简单，节省上课时间，如果教师认为教学任务比较繁重、教学时间比较紧张，无法保证后续内容时间的把控，那么可以采用这种简洁的方式进行引入工作。

由引例我们可以得到当X是离散型随机变量时，其数学期望的定义为：设离散型随机变量X的分布律为：P{X=xk}=pk，k=1，2，…，n，如果级数绝对收敛，则称级数为随机变量X的数学期望（或均值），记为E（X）（在不产生混淆的情况下，也可记为EX），即

接着可通过一个例题来求解数学期望，从而加深学生对定义的理解和记忆。例如下面这则简单例子：掷一枚六面骰子，已知其各面朝上的可能性是相同的，则掷得的点数的数学期望是多少呢？

此时可以引导学生思考：骰子的任何一面都不可能为3.5，然而最后算得的掷得的点数的数学期望却是3.5，这说明了什么问题呢？这说明了期望值并不一定等同于常识中的“期望”，“期望值”也许与每一个结果都不相等。换句话说，期望值是该随机变量取值的平均数，期望值并不一定包含于随机变量的取值集合里，这就加深了学生对数学期望定义的理解和把握。

二、关于如何“引申”到连续型随机变量期望的定义

对于连续型随机变量其值充满整个区间，且取每一特定值的概率均为0，因此不能直接利用上述离散型随机变量期望定义求其数学期望。但可将连续型随机变量离散化，再由离散型随机变量的数学期望的定义引申出连续型随机变量的数学期望的定义。

设连续型随机变量为X，它的取值范围可视为（-∞，+∞），把（-∞，+∞）划分为无数个小区间，[x0，x1]，[x1，x2]，…，[xn-1，xn]，（n→∞），则X在其中任意一个小区间[xk-1，xk]中取值的概率近似为f（xk-1）Δxk-1，其中f（xk-1）是X的概率密度函数在xk-1的值（其实是在xk-1附近的值，可近似这样认为），Δxk-1=xk-xk-1。由离散型随机变量期望的定义：X的数学期望就是X能取到的每个值乘以它取这个值的概率的积的和，即可引申得到连续型随机变量的数学期望为：

由此得到连续型随机变量数学期望的定义为：设连续型随机变量X的概率密度函数为f（x），若积分xf（x）dx绝对收敛，则积分的值为随机变量X的数学期望，记为E（X），即：

三、关于如何“过渡”到方差

因为方差本身就是一种数学期望，但是如何引出“方差”这一数学期望却是要费一点心思的。比如说现在我们面前摆放着两只手表，它们每日的走时误差（以分为单位）分别以随机变量和表示，其分布律如下。

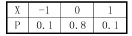
图1 随机变量X的分布律表

图2 随机变量Y的分布律表

从图1、图2中容易看出：E（X）=E（Y）=0，因此无法从期望评选出哪只手表质量更优。但直观可看出：第一只手表的每日走时误差X与其均值得偏离程度更小，走时更精确，质量更好。此时可引导学生思考：我们应该选择什么样的一个量来表示随机变量与其均值的偏离程度呢？直接用X-E（X）显然不太好，因为它有正负号差别，不便于比较大小。那么用好不好呢？它已经避免了正负号的讨论，显然也不太好，因为它涉及到如何脱去绝对值的讨论。此时我们可能想到用（X-E（X））2这个量比较好，因为它永远是非负的，便于比较大小，又不用考虑脱去绝对值的问题，但是我们又想到X的取值是随机的，此时表示随机变量与其均值的偏离程度应该考虑X能够取到的所有的点，而并非单一的一个点。那么怎么样才能考虑到所有的点呢？此时我们可以回顾之前期望的定义，会发现期望正是考虑了随机变量取值的所有的点的情况。因此，再在（X-E（X））2上加上期望符号就变成了，这就是用来表示随机变量与其均值的偏离程度的量，我们称它为方差，记为：，由此可得到方差的定义：设X是一个随机变量，若存在，则E为X的方差，记为D（X）或Var（X），即：D

四、结语

通过实际的教学实践，我们发现“数学期望”概念对于许多同学来说是非常抽象的，因此，对它概念的讲解就应该是我们必须注意的地方。本文是笔者对“数学期望”概念的讲解的一点经验总结，希望能对概率论与数理统计的教学起到一点“抛砖引玉”的作用。

[1]盛骤，谢式千，潘承毅.概率论与数理统计[M].北京：高等教育出版社，2008.

[2]李正耀，周德强.大学数学——概率论与数理统计[M].北京：科学出社，2009.

[3]熊欧，仇海全，武洁.数学期望的教学方法新探[J].科技信息，2010，（3）.

G642.41

A

1674-9324（2014）45-0199-03

长江大学教研项目（JY2011023）

曹小玲（1981-），女，数学与应用数学系，讲师，现主要从事数字图像处理和高等工程数学的教学与研究工作。