Phenomenological model for torsional galloping of an elastic flat plate due to hydrodynamic loads*

FERNANDES Antonio Carlos, ARMANDEI Mohammadmehdi

Department of Naval and Ocean Engineering, COPPE/UFRJ, Rio de Janeiro, RJ, Brazil, E-mail: marmandei@oceanica.ufrj.br

Phenomenological model for torsional galloping of an elastic flat plate due to hydrodynamic loads*

FERNANDES Antonio Carlos, ARMANDEI Mohammadmehdi

Department of Naval and Ocean Engineering, COPPE/UFRJ, Rio de Janeiro, RJ, Brazil, E-mail: marmandei@oceanica.ufrj.br

(Received September 6, 2013, Revised January 6, 2014)

This study investigates the torsional galloping phenomenon, an instability type flow-induced oscillation, in an elastic structure due to hydrodynamic loads into the water current. The structure applied here is a rectangular flat plate with an elastic axis in its mid-chord length. The elasticity is provided by torsion spring. The flat plate has only one degree of freedom which is rotation in pure yaw about its axis. It is observed that as the current speed is higher than a critical velocity, the flat plate becomes unstable. The instability leads to torsional galloping occurrence, as a result of which the flat plate begins to yaw about the elastic axis. By testing two different chord lengths each with several torsion spring rates, the flat plate behavior is investigated and three different responses are recognized. Then, a phenomenological model is developed with the original kernel in the form of the van der Pol-Duffing equation. The model explains these three responses observed experimentally.

torsional galloping, flow-induced oscillation, phenomenological model, van der Pol-Duffing equation

Introduction

Flow-induced oscillations are results of the interaction between fluid flow and elastic structures. They are usually tried to be suppressed, because of their destructive effects on structures. Nevertheless, if they are exploited, they have a great potential to be applied in energy extraction. Its feasibility has been proved through several scaled models and prototypes[1,2]. Therefore, to have an analytical approach to deal with flowinduced oscillation might be of interest, for both suppression and exploiting.

Flow-induced oscillations are classified in two categories; resonance type and instability type as shown in Fig.1[3]. In the resonance type, the flow-induced forces and moments do not depend on the structural motion. In other words, the elastic structure begins to oscillate if the frequency of the oscillatory forces corresponds to its natural frequency. The oscillatory force can be induced either by the oscillating incoming flow, which leads to buffeting, or by the vortex shedding, which causes vortex-induced vibration (VIV). On the other hand, in the instability type, the forces vary with time as a result of the motion of the structure, and increase the oscillation amplitude. The instability is called as flutter when the resulting oscillation is in two or more coupled degrees of freedom, and as galloping when the oscillation has only one degree of freedom with relatively high amplitude, whether translational or torsional.

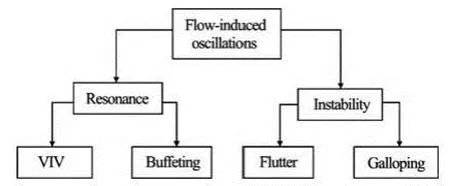
Fig.1 Flowchart for flow-induced oscillation

There are different ways to model flow-induced oscillations. In flow-induced oscillations of resonance type, since the driving force or moment comes from the oscillatory stream, its structure is nearly sinusoidal[4]. Therefore, the harmonic modeling is very much adequate. On the other hand, in flow-induced oscilla-tions of instability type, the fluid-induced moment varies with time due to the motion of the elastic structures. Hence, the flow-induced moment on the elastic structure will vary with the frequency of oscillation. In this case, the harmonic modeling is not necessarily appropriate, and thus needs to be superseded.

One of the alternatives to define the flow-induced force or moment in the instability type flow-induced oscillation is to apply some frequency-dependent and dimensionless coefficients known as the flutter derivatives[5]. There are two different methods to identify these coefficients: analytical methods and experimental techniques. The analytical methods are based on the unsteady inviscid flow theory, like the Theodorsen theory. However, the Theodorsen theory is not useful for high amplitudes, because of the separation effects. Furthermore, the experimental techniques developed to find the flutter derivatives are based on either the forced vibration or the free vibration of the elastic structure[6]. In the forced vibration tests a prescribed motion is forced on the structure, whereas in the free vibration tests the structure is subjected to the flow-induced effects. In each test, then, the structure’s motion is measured, and the flutter derivatives are calculated from the measurement of the motion.

Phenomenological modeling is another approach that helps to understand the physics of flow-induced oscillations by allowing accessible analytical consideration. The earlier studies have developed phenomenological models for VIV following the idea of wake oscillator[7,8]. Moreover, Facchinetti et al.[9]considered the wake oscillator coupled with structure oscillator to analyze the low-order models for VIV. The same approach was followed by Rosetti et al.[10]to develop a numerical tool to represent the fluid-structure interaction of monocolumn platforms during the occurrence of vortex-induced motions.

Along with flow-induced oscillation, phenomenological modeling has also been reported in flow-induced rotations. One of the studies made by Anderson et al.[11]applied a phenomenological model to investigate the transition between fluttering and tumbling for a rigid card falling in air. Furthermore, Mirzaeisefat and Fernandes[12]considered a phenomenological model to analyze the flow-induced rotation for a flat plate hinged at center into the water current.

The current study investigates torsional galloping, an instability type flow-induced oscillation, of an elastic structure into the water current. The structure in this study is a rectangular flat plate, with an elastic axis in its mid-chord length. The flat plate has only one degree of freedom which is rotation in pure yaw about its elastic axis. The hydrodynamic loads on the same structure have been described through the work of other investigators[13,14]. The elasticity is provided by attaching a torsion spring to the flat plate. As long as the water is stagnant, any disturbance on the flat plate will decay as a result of the energy dissipation due to the structural damping. However, in the presence of currents, the dynamics of the flat plate will be influenced due to the additional external hydrodynamic moments. Consequently, if the current speed is higher than a critical velocity, the structural damping term is balanced, the flat plate becomes unstable and torsional galloping occurs.

Through this study the torsional galloping of the elastic flat plate is observed experimentally. Although the problem is of similar character to the one studied systematically by Poirel et al.[15], it occurs at relatively high angles of attack with flow separation. The experimental tests are first described along with torsional galloping observation and response. The establishment of a phenomenological model is then outlined, using which the flat plate responses to the hydrodynamic loads are discussed as torsional galloping thresholds.

1. Torsional galloping, observation and response

1.1Experimental tests

In order to observe torsional galloping in the water current, some experiments were conducted in the current flume of Laboratory of Waves and Currents (LOC) in COPPE/UFRJ. The current flume has 22 m length, 1.4 m width and 0.5 m depth, and the maximum current speed attainable in the flume is 0.5 m/s. The free stream current speed was recorded using an electronic flow meter.

A set-up was prepared consisting of an aluminum-made rectangular flat plate with 0.6 m height (ρAl=2 700 kg/m3), and an elastic axis in its midchord length. The flat plate’s yaw was captured via a Qualisys motion capture system (2 Oqus cameras and the QTM software version 1.1). In the experiments, two different chord lengths were utilized,c=0.2 m andc=0.3 m. For these chord lengths, the maximum Reynol5ds numbers in the current flume are 105and 1.5×10, respectively. Nevertheless, the current problem has minimal Reynolds dependency due to the fact that it is a large angle of attack problem. The water depth was kept to beh=0.45 m during the tests. The elasticity was provided via attachment of a torsion spring to the flat plates. Several torsion springs were utilized to assess the effect of the stiffness on torsional galloping. All torsion springs used were calibrated and their coefficients were obtained. Several decay tests were also conducted in the air in order to find the structural damping ratio. Finally, its mean value was found to beζS=0.1. Figure 2 shows the photograph of the experimental set-up and the schematic top view of the system.

Basically, the uncertainties in the measurementscome from three sources: experimental set-up, the data acquisition devices, and truncation error that are taken into account in numerical analysis. In order to check the first, each test was performed several times during the experiments, to assure the repeatability. The data acquisition devices also were configured to reduce the uncertainties as much as possible. For instance, the Qualisys motion capture system was set at 100 frames per second to capture the displacement with more clarity. Furthermore, calibration tests on the flowmeter demonstrated that its data acquisition precision is high, with about 0.1 % of uncertainty.

Fig.2(a) Photograph of the experimental set-up

Fig.2(b) Schematic top view of the system

1.2Torsional galloping observation

Some experiments were conducted in order to observe the instability in the structure. In the experiments, the current speed ()Uwas increased slightly from zero. It was observed that as the current speed is higher than a critical velocitycrit()U, the flat plate becomes unstable. The transition to instability is illustrated in Fig.3.The aforementioned instability leads to torsional galloping, exemplified in Fig.4. The critical velocities obtained for each chord length are listed in Table 1.

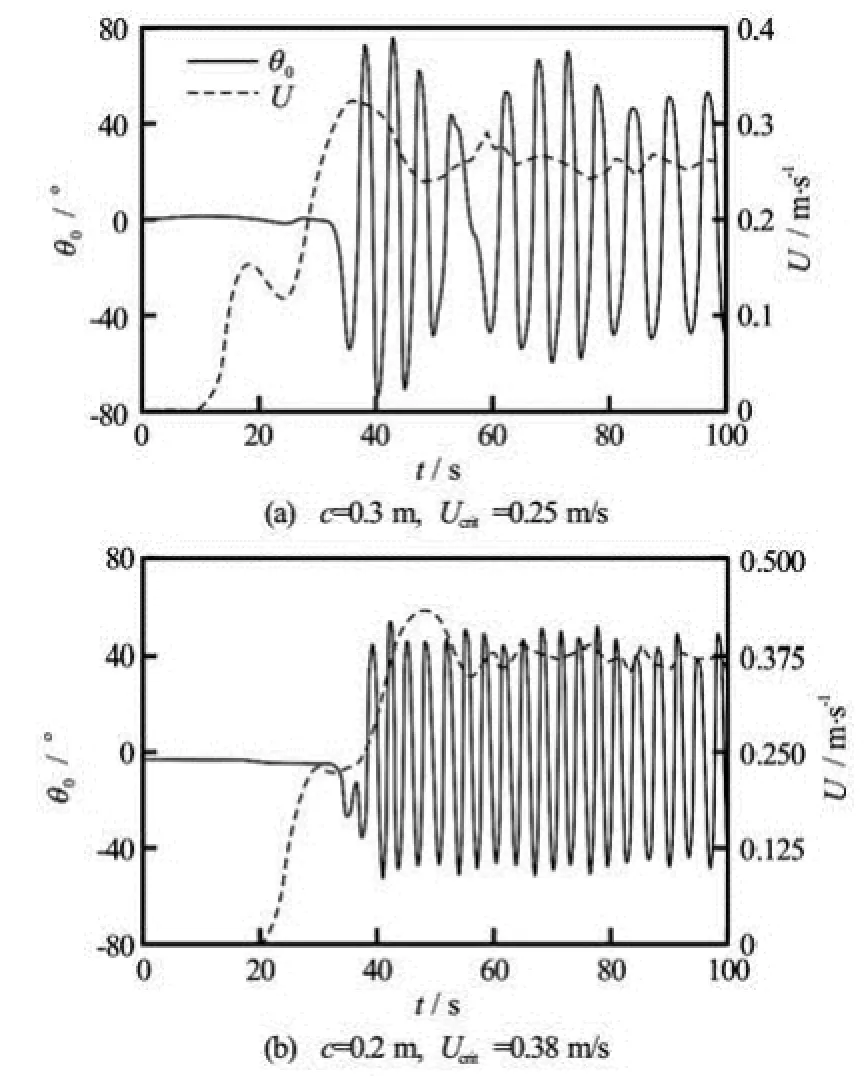
Fig.3 Transition from the stable still condition to oscillatory instability, =kθ0.97 Nm/rad for both (a) and (b)

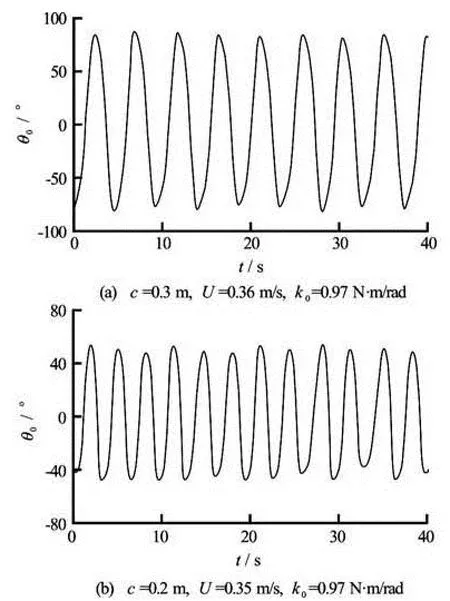
Fig.4 Two examples of torsional galloping time series, =kθ0.97 Nm/rad for both (a) and (b)

Table 1 Critical velocity values observed in the experiments

1.3Torsional galloping response

The response amplitude (θ0) and the response frequency (f) of the flat plate in torsional galloping are functions of natural frequency (fn), water depth (h), chord length (c), and current speed (U). A dimensional analysis of these parameters leads to

whereARis the aspect ratio,rnUthe reduced velocity, andΩthe frequency ratio. They are respectively defined by

The natural frequency is defined by

Fig.5 Response amplitude (θ0) in terms of Urnfor both AR-1 s. Constant lines point torsional galloping amplitude (θˆ)

Fig.6 Response frequency (f) in terms of Urfor both AR-1s. Constant lines point torsional galloping frequency (fˆ)

Table 2 Torsional galloping amplitude) and torsional galloping frequency (ˆ), together with Urnminand Urnmaxfor each AR-1

Table 2 Torsional galloping amplitude) and torsional galloping frequency (ˆ), together with Urnminand Urnmaxfor each AR-1

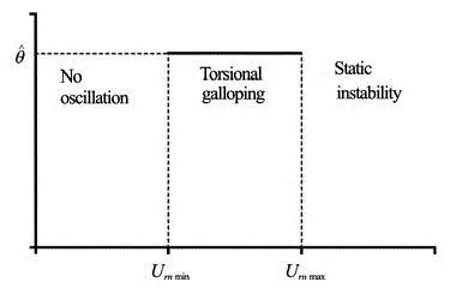
Fig.7 Three intervals of Urn, No oscillation for Urn≤Urnmin, Torsional galloping for Urnmin＜Urn＜Urnmax, and static instability for Urn≥Urnmax

In order to see the behavior of the flat plate out of the rangeUrnmin＜Urn＜Urnmax, some experiments were conducted. Eventually, three intervals ofUrnwere observed, wherein the flat plates show different behaviors: No oscillation forUrn≤Urnmin, where every perturbation is highly damped, Torsional galloping forUrnmin＜Urn＜Urnmax, where any perturbation results in a self-sustained oscillation in the flat plate, and Static instability forUrn≥Urnmax, where any slight perturbation makes the flat plates undergo large torsional deformations. These three intervals are depicted in Fig.7.

2. Phenomenological model

Consider a one degree of freedom elastically supported rigid flat plate of chord lengthc, constrained to rotate in pure yaw to a uniform water current of free stream speedU. The equation of motion of the structure is described by Newton’s second law

wherebis damping coefficient, and dots mean derivative with respect to the dimensional timet. Given the fact that the hydrodynamic forces on the structure will vary with the frequency of oscillation, a convenient way to express the hydrodynamic moment on the right hand side of Eq.(7) is as follows[5]

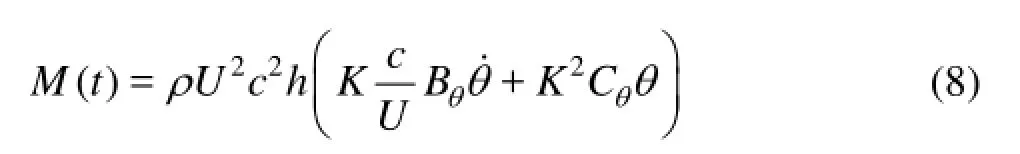
whereBθandCθ, are the flutter derivatives, which are functions of frequency, andKis the reduced frequency which is defined as follows

Replacing ()M tfrom Eq.(8) andKfrom Eq.(9) into Eq.(7), yields

It is known that the whole instability type flowinduced oscillations including torsional galloping are damping-controlled phenomena, since their occurrence involves zero damping[5]. As a result, in order for them to be torsional galloping, the damping term in Eq.(10) should be set equal to zero. Note that the damping coefficientbis expressed by

In order to examine the response characteristics in the post-critical state, it has been suggested that the problem must be formulated in the nonlinear state[18]. Therefore, the elasticity term in Eq.(10) is proposed to be

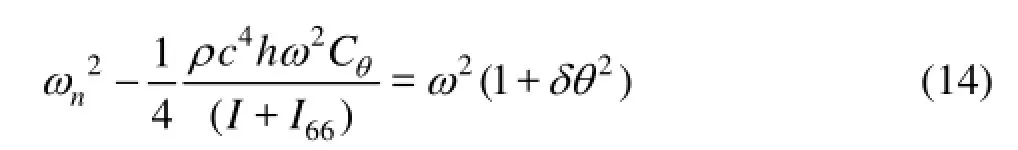
whereδis the scale factor for the nonlinearity of torsional galloping limit cycle. Solving Eq.(14) to identify the parameterCθyields

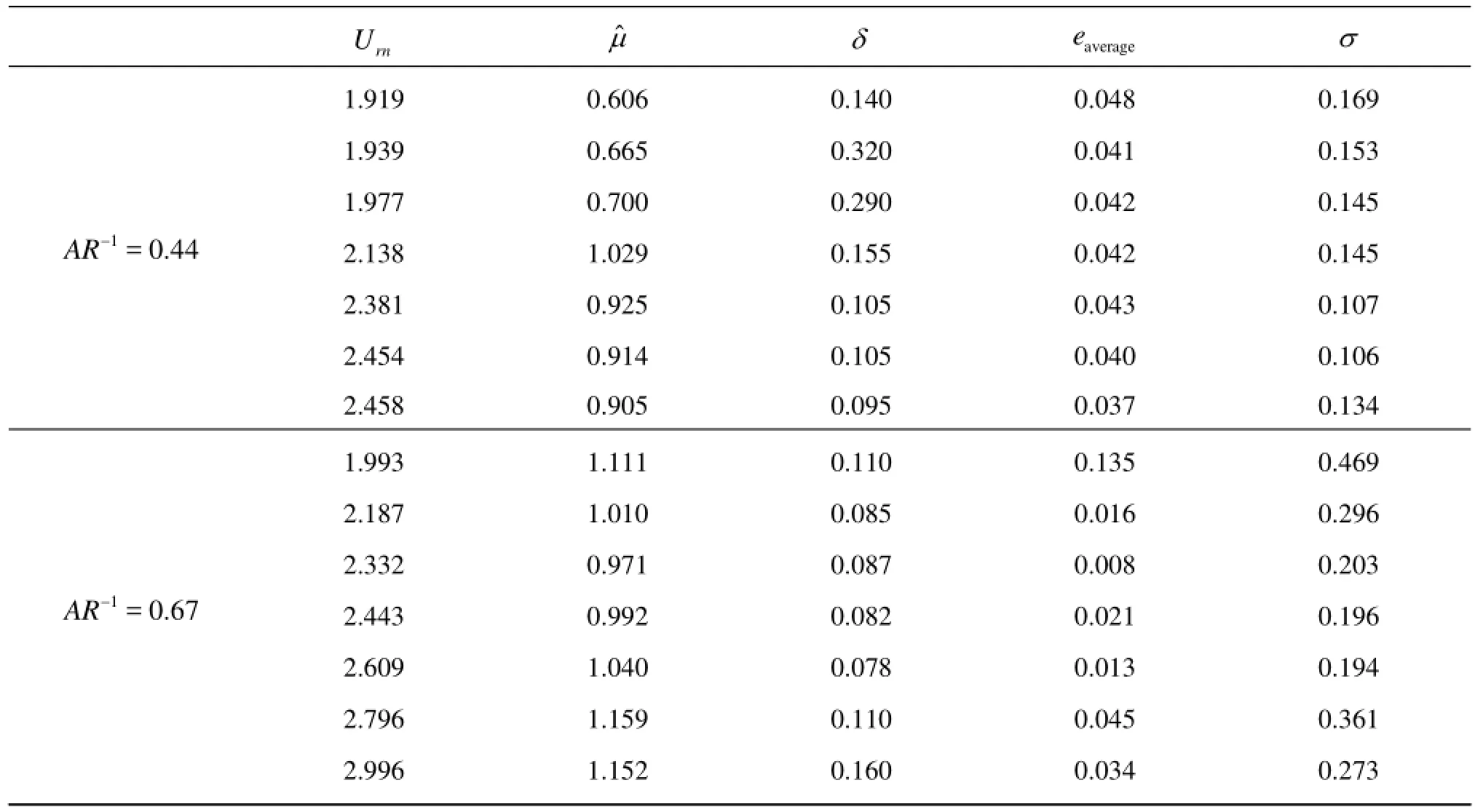
Table 3 Values of the constants ˆμ, δ,averagee and σ

Furthermore, the linear viscous damping model is questionable from the point of view of the physical dissipative mechanisms and should be improved[15]. To this end, the damping coefficient in Eq.(10) is proposed to be replaced with the term2εθ, whereεis a constant with the physical dimension of the damping coefficient. With this replacement, and also replacingBθandCθaccording to Eqs.(12) and (15), Eq.(10) becomes

The equation above is expressed in the dimensionless form, using the dimensionless time =tτω

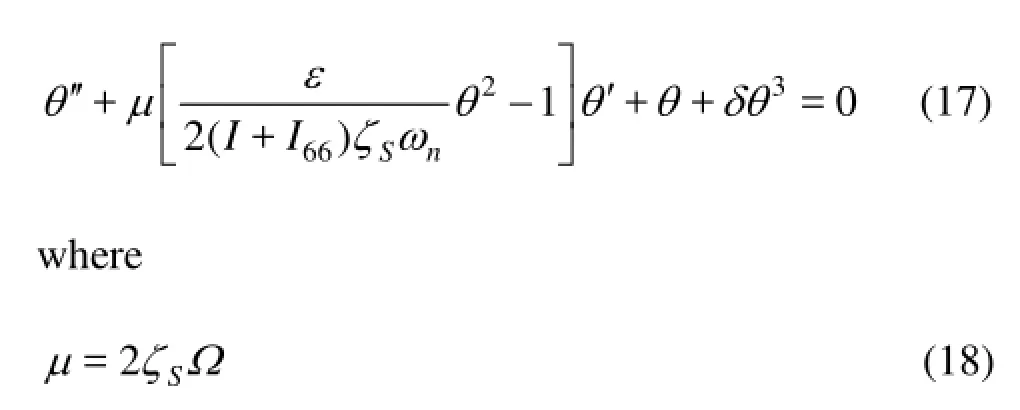
In order to identify the coefficient of nonlinear dampingε, the following change of variable is applied

Then, Eq.(17) is written in the following fashion

Based on the fact that for Equation 20 the amplitude isγ0=2[19],εcan be identified as follows

Then, replacingεfrom Eq.(21) into Eq.(17) yields

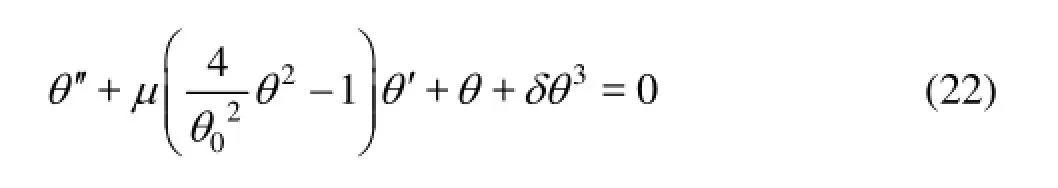
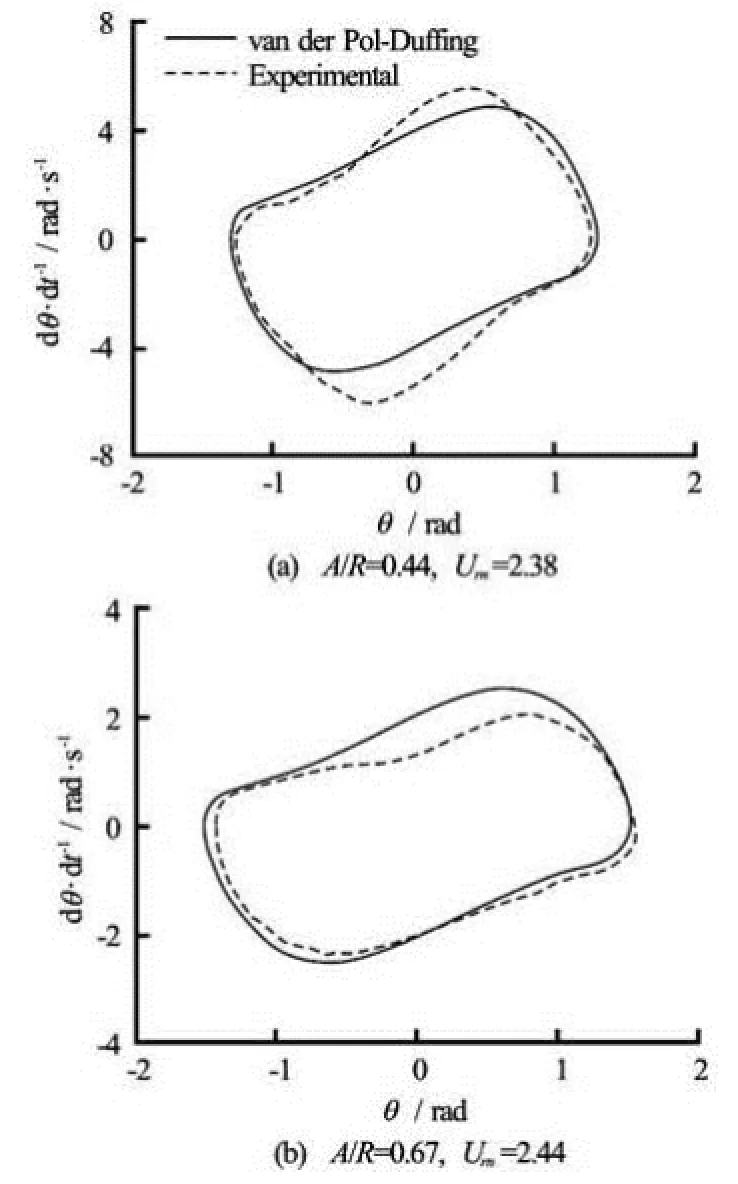
Fig.8 Average phase portrait obtained from the experiment (Dashed line) compared to phase portrait obtained by solving Eq.(22) (Solid line)

3. Torsional galloping thresholds

Using the van der Pol-Duffing equation derived as a phenomenological model for torsional galloping, the three behaviors described above can be explained in the phase space. The trajectories of each behavior are given through Fig.9. In the case of No oscillationμ＞(Fig.9(a)), it is seen that every trajectory is converged to the center. In other words, there is a stable fixed point at the origin of the phase portrait, and every trajectory is a stable spiral. On the other hand, in Static instability μ＜(Fig.9(c)), every trajectory is diverged from the center. Likewise, there is an unstable fixed point at the origin of the phase portrait, and every trajectory is an unstable spiral.

In the case of Torsional galloping μ=(Fig.9(b)), every trajectory, whether started within the limit cycle or out of it, approaches to the limit cycle. In fact, the damping term can be both positive and negative along the trajectory. However, the positive and negative damping terms reach balance so that the amplitude of oscillation is preserved.

Fig.9 Trajectories of the flat plate responses in phase space

Basically, torsional galloping in engineering is mostly known as a destructive phenomenon. The most famous example of destruction caused by torsional galloping is the Tacoma Narrows Bridge which collapsed in 1940[21]. Nevertheless, because of its robustness this phenomenon can be used for energy extraction from the fluid flow[2]. Overall, the phenomenological model developed here may be useful in the analyses related to both categories.

4. Conclusions

Torsional galloping phenomenon of a flat plate into the water current has been investigated through this study. First, the experiments have been conducted in order to observe the responses of the flat plate to the hydrodynamic loads. Through the experiments, three different responses have been observed in the flat plate, No oscillation forUrn≤Urnmin, where every perturbation forms a stable spiral in the phase space, Static instability forUrn≥Urnmin, where any slightperturbation forms an unstable spiral, and Torsional galloping forUrnmin＜Urn＜Urnmax, where any perturbation results in a limit cycle.

Then, in order to have a better understanding of the underlying physics, a phenomenological model has been developed for torsional galloping, with the original kernel in the form of the van der Pol-Duffing equation. Through the modeling procedure, a new parameter called torsional galloping parameter (μ) has been found. This parameter is represented as an indicator for the torsional galloping occurrence. Using the phenomenological model, the flat plate responses to the hydrodynamic loads have been investigated in the phase space. Torsional galloping occurs whenμ=ˆ, whereas No oscillation corresponds toμ＞, and Static instability toμ＜ˆ.

The present work aims to introduce the phenomenological model of torsional galloping. The function of this model in the assessment of the energy extraction capability of torsional galloping is studied and will be presented in a subsequent paper of the authors.

Acknowledgements

The authors would like to acknowledge gratefully CNPq (Conselho Nacional da Pequisa) and also COPPETEC foundation (Coordenação de Projetos, Pesquisas e Estudos Tecnológicos) for the funding of this research. Also, the LOC’s staff members are appreciated for their considerable help in the experimental work of the research.

[1] BERNISTAS M. M., RAGHAVAN K. and BENSIMON Y. et al. VIVACE (Vortex Induced Vibration Aquatic Clean Energy): A new concept in generation of clean and renewable energy from fluid flow[J]. Journal of Offshore Mechanics Arctic Engineering, 2008, 130(4): 041101.

[2] ARMANDEI M., FERNANDES A. C. Marine current energy using torsional galloping based turbine[C]. Offshore Technology Conference. Houston, TX USA, 2013.

[3] Van OUDHEUSDEN B. W. Investigation of an aeroelastic oscillator: Analysis of one-degree-of-freedom galloping with combined translational and torsional effects[R]. LR-707, Faculty of Aerospace Engineering, Delft, The Netherlands: Delft University of Technology, 1992.

[4] SARPKAYA T. A critical review of the intrinsic nature of vortex-induced vibrations[J]. Journal of Fluids Structures, 2004, 19(4): 389-447.

[5] PAÏDOUSSIS M. P., PRICE S. J. and De LANGRE E. Fluid-structure interactions: Cross-flow-induced instabilities[M]. New York, USA: Cambridge University Press, 2011.

[6] SARKAR P. P., CARACOGLIA L. and HAAN F. L. et al. Comparative and sensitivity study of flutter derivatives of selected bridge deck sections, Part 1: Analysis of inter-laboratory experimental data[J]. Engineering Structures, 2009, 31(1): 158-169.

[7] BIRKHOFF G., ZARANTANELLO E. H. Jets, wakes and cavities[M]. New York, USA: Academic Press, 1957.

[8] BISHOP R. E. D., HASSAN A. Y. The lift and drag forces on a circular cylinder oscillating in a flowing fluid[J]. Proceedings the Royal Society London A, 1964, 277(1368): 51-75.

[9] FACCHINETTI M. L., De LANGRE E. and BIOLLEY F. Coupling of structure and wake oscillators in vortexinduced vibrations[J]. Journal of Fluids Structures, 2004, 19(2): 123-140.

[10] ROSETTI G., GONÇALVES R. and FUJARRA A. L. C. et al. Parametric analysis of a phenomenological model for vortex-induced motions of monocolumn platforms[J]. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 2011, 33(2): 139-146.

[11] ANDERSEN A., PESAVENTO U. and WANG Z. J. Analysis of transitions between fluttering, tumbling and steady descent of falling cards[J]. Journal of Fluid Mechanics, 2005, 541: 91-104.

[12] MIRZAEISEFAT Sina, FERNANDES Antonio Carlos. Stability analysis of the fluttering and autorotation of flow-induced rotation of a hinged flat plate[J]. Journal of Hydrodynamics, 2013, 25(5): 755-762.

[13] MIRZAEI SEFAT S., FERNANDES A. C. Flow induced rotation of a flat plate subjected in uniform current based on the streamline theory[C]. Proceedings of the ASME, 30th International Conference of Ocean, Offshore and Arctic Engineering. 2011.

[14] FERNANDES A. C., MIRZAEI SEFAT S. and COELHO F. M. et al. Towards the understanding of manifold fluttering during pendulous installation: Induced rotation of flat plates in uniform flow[C]. Proceedings of the ASME, 29th International Conference of Ocean, Offshore and Arctic Engineering. Shanghai, China, 2010.

[15] POIREL D., HARRIS Y. and BENAISSA A. Self-sustained aeroelastic oscillations of a NACA0012 airfoil at low-to-moderate Reynolds numbers[J]. Journal of Fluid Structures, 2008, 24(5): 700-719.

[16] GHADIMI P., PASELAR BANDARI H. and BAKHSHANDEH ROSTAMI A. Determination of the heave and pitch motions of a floating cylinder by analytical solution of its diffraction problem and examination of the effects of geometric parameters on its dynamics in regular waves[J]. International Journal of Applied Mathematical Research, 2012, 1(4): 611-633.

[17] FERNANDES A. C., MIRZAEISEFAT S. and COELHO F. M. et al. Experimental investigation of flow induced rotation of hinged plates with shapes to avoid fluttering[C]. Proceedings of the ASME, 30th International Conference of Ocean, Offshore and Arctic Engineering. Rotterdam, The Netherlands, 2011.

[18] NÁPRSTEK J. Nonlinear stability of flutter-type vibration in wind[C]. 7th International Conference of Flow Induced Vibration (FIV 2000), Luzern, Switzerland, 2000, 445-454.

[19] LÓPEZ J. L., ABBASBANDY S. and LÓPEZ-RUIZ R. Formulas for the amplitude of the van der Pol limit cycle through the homotopy analysis method[J]. Scho-larly Research Exchange, 2009, 2009:doi:10.3814/ 2009/854060.

[20] OUYANG Ke-Jian, TANG Jia-Shi and LIANG Cui-Xiang. Amplitude control of limit cycle in a van der Pol Duffing system[J]. Chinese Physics B, 2009, 18(11): 4748-4753.

[21] MATSUMOTO M., SHIRATO H. and YAGI T. et al. Effects of aerodynamic interferences between heaving and torsional vibration of bridge decks: The case of Tacoma Narrows Bridge[J]. Journal of Wind Engineering Industrial Aerodynamics, 2003, 91(12-15): 1547-1557.

10.1016/S1001-6058(14)60007-X

* Biography: ARMANDEI Mohammadmehdi (1982-), Male, Postdoctor Researcher