基于偏正态分布的SN-ARCH(q)模型及应用
徐 燕,陈平雁
(南方医科大学 公共卫生与热带医学学院生物统计学系,广州 510515)
时间序列分析在生物、医学、气象、天文、地质、经济等领域广泛应用,尤其是在经济金融领域,如汇率、股票价格、收益率等。由于各时刻的条件均值和方差难以满足常数的假设,Engle(1982)提出自回归条件异方差模型,条件均值和方差分别依赖于t时刻之前的观察值和误差平方,并表示为过去值的函数,这意味着其条件方差非常数,从而满足了要求。
Hagan和Leonhard(1976)在正态分布中引入刻画偏度的形态参数而得到新的分布称为Skew Normal Distribution,简称SN分布,处理偏态数据效果良好[1]。
本文首先介绍SN分布概念,然后给出SN-ARCH(q)模型及参数中位数无偏估计,最后报道实验结果。
1 SN分布
近年来基于某些对称分布的偏斜分布族被大量研究,如正态分布、t分布、Cauchy分布等[1,2,3]。这类问题的关键在于引入偏斜参数后得到参数方程的分布形式及参数估计。
1.1 SN分布
引理1[1]令f0是一维零对称概率密度函数,G是一维分布函数,G'存在并且是一个零对称密度函数,则对任一奇函数w(˙),有

是一个概率密度函数。
由此引理,对任意零对称密度函数f0,可以通过扰动函数得到一个新的密度函数 f,并且 f0是 f的特殊情况,即取w(x)≡0时。
Azzzlini(1985)取w(y)=αy,α是常数,即得到单变量SN分布。
定义1[1]令Y是一个连续随机变量,ϕ和Φ是N(0,1)密度函数和分布函数。若Y的密度函数满足:
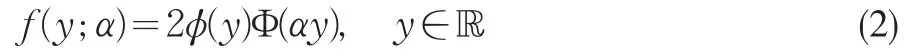
则称Y服从带参数a,a∈ℝ,的SN分布,记为y~SN(a)。
称a,a∈ℝ,为形状参数,其决定了概率密度函数的形状,a>0时Y正偏,a<0时Y负偏, ||a增加偏度随之增加。当a=0时,即N(0,1)。文献[1]有SN分布与正态分布的关系的研究。
一般的,令Z~SN(a),且Y=ξ+ωZ,其中ξ∈ℝ,ω>0,则Y的概率密度函数是:
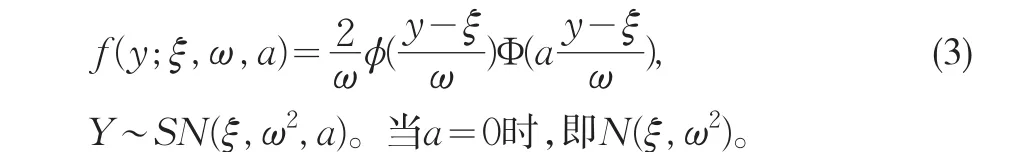
1.2 矩估计
Pewsey(2000,2006)给出SN分布重新参数化后的矩估计,Arellano等(2008)给出重新参数化和原始参数两种形式下的Fisher信息矩阵。下面综述文献[3,4]给出SN分布参数矩估计。
设Y~SN(ξ,ω2,a),则
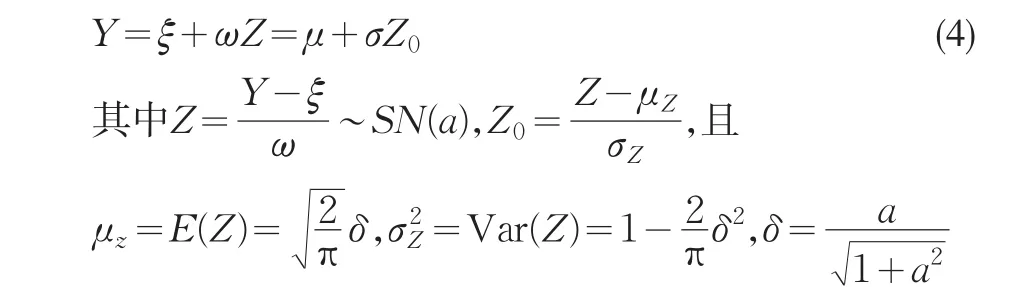
重新参数化后记为(μ ,σ2,γ1),由(4)得
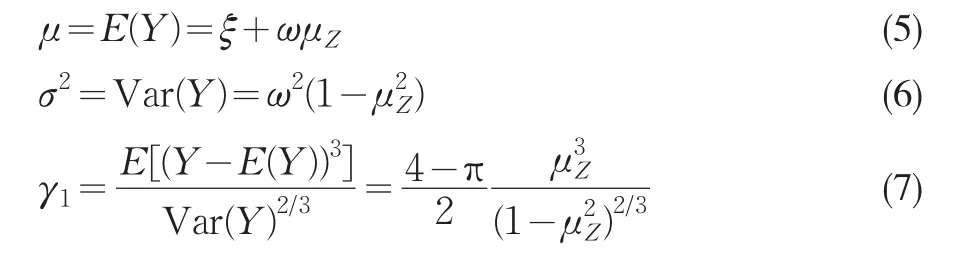
其中γ1表示偏度系数。
解方程(5)(6)(7),得
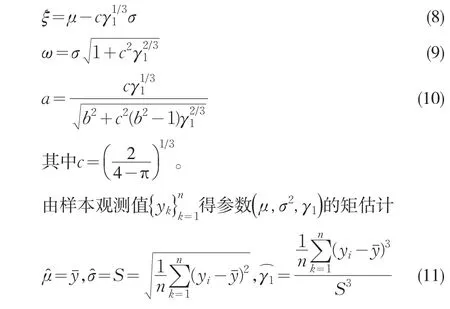
将(11)带入(8)(9)(10),即得参数(ξ,ω2,a)的矩估计
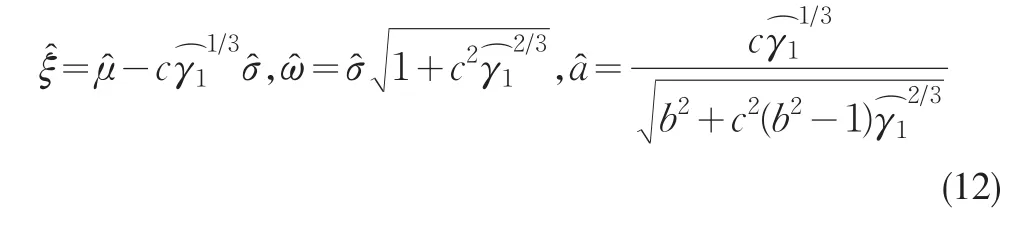
2 SN-ARCH(q)模型
2.1 ARCH模型
定义2(ARCH(q)模型)[5]设是零均值序列无关过程,如果
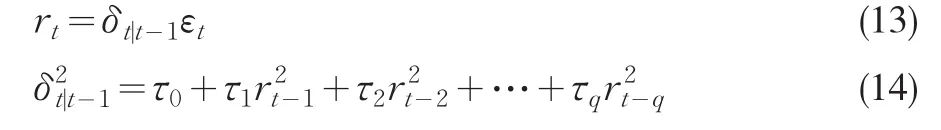
2.2 SN-ARCH模型中位数的无偏估计
Engel(1982)给出ARCH模型参数极大似然估计的Newton-Raphson算法,此算法缺点在于不能保证每一步输出值非负性;Weiss(1984,)和Ling(2000)分别在四阶矩和二阶矩条件下给出ARCH模型参数极大似然估计的渐进性质;Lee等(1993)采用得分函数得到模型检验;Hong(1996)用谱方法给出ARCH模型的单边检验。Shi等(2003)给出一定条件下的ARCH(0,1)中位数无偏估计[6]。下面构造SN-ARCH(q)的中位数无偏估计。
简单的,考虑SN-ARCH(1),即

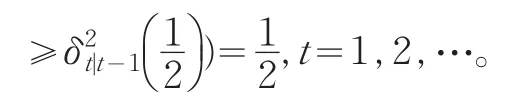
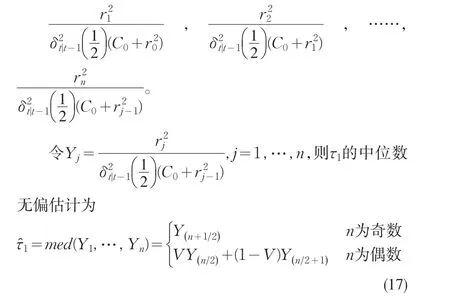
其中V是与Y1,…,Yn独立的随机变量,且满足P(V=0)=P(V=1)=Y(1),…,Y(n)即Y1,…,Yn的次序统计量。
3 实验结果
基于R统计软件,对S&P500收益率序列(2001.02.01至2012.02.01,N=3280,0.004±0.0220)在0.05的检验水准下进行Bera-Jarque正态性检验,拒绝正态分布假设(B-J=1011.000,P<0.001),偏度(Skewness=-0.2320)显著小于 0。自相关函数以偏离零均值的形式震荡,以正弦曲线形式缓慢衰减。ARCH-Mcleod-Li残差检验,当残差平方自相关系数的滞后阶数从1到27时检验全部显著(P均小于0.01),存在条件异方差性。建立SN-ARCH模型,模型参数估计如表1所示。

表1 S&P500收益率序列拟合模型参数估计
对上述模型残差进行McLeod-Li检验,残差及残差平方序列在多项滞后时的统计结果接受原假设,说明SN-ARCH(1)模型能够很好的消除原序列的异方差性。
对模型分布进行Pearson拟合优度检验[7],比较理论分布与实际分布的接近程度。在0.05的检验水平下不拒绝原假设(χ2=31.675,P=0.891),即模型选择合理。
4 总结与讨论
本文从实际序列不服从正态分布的前提假设入手,在ARCH模型中引入SN分布,建立SN-ARCH(q)模型,给出参数中位数无偏估计,实验结果通过Pearson拟合优度检验,证明模型选择合理。
SN分布的参数估计是比较麻烦的问题,它多了一个参数且密度函数不对称,因此对于传统的取对数变换,然后对参数求偏导数,从而得到极大似然估计的方法效果不佳。对于ARCH模型破坏了方差不变的前提假设,故采用了非参数的中位数估计,与传统的Yule-Walker估计和条件最小二乘估计相比更准确有效。
[1]Azzalini A.A Class of Distribution which Includes the Normal Ones[J].Scand.J.Statist.,1985,12(2).
[2]Shaun A.Bond.A Review of Asymmetric Conditional Density Functions in Autoregressive Conditional Heteroskedasticity Models[Z].2002.
[3]Pewsey A.Modelling Asymmetrically Distributed Circular Data Using the Wrapped Skew Normal Distribution[J].Environ.Ecol.Stat.,2006,(13).
[4]Pewsey A.Problems of Inference for Azzalini,s Skew-normal Distribution[J].J.Appl.Stat.,2000,(27).
[5]Jonathan D.Cryer,Kung-Sik Chan.Time Series Analysis with Applications in R[M].New York:Springer Science Business Media,2008.
[6]Shi N.Z.Wang D.H.Median Unbiased and Maximum Likelihood Estimations of ARCH(0,1)Coefficient[Z].Statistics Simulation and Computation,2003.
[7]Palm F.C.,Vlaar P.J.G.Simple Diagnostics Procedures for Modelling Financial Time Series[J].Allgemeines Statistisches Archiv,1997,(81).

