渐近线性四阶半正边值问题正解的分歧结构
刘 瑞 宽
(西北师范大学 数学与统计学院,兰州730070)
0 引言及主要结果
四阶常微分方程在工程和物理等领域应用广泛,其中两端简单支撑的弯曲弹性梁平衡状态可用四阶边值问题
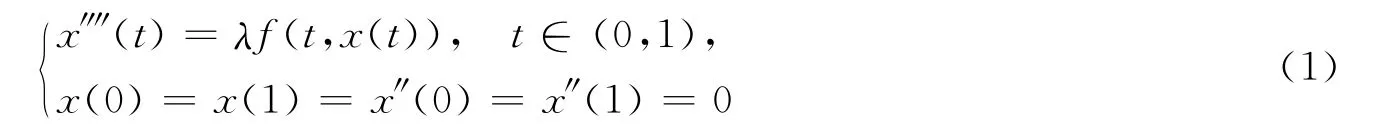
描述[1-2],由于其应用广泛,已引起人们广泛关注[3-12].
特别地,马如云等[3]运用Krasnoselskii锥映射不动点定理研究了四阶边值问题
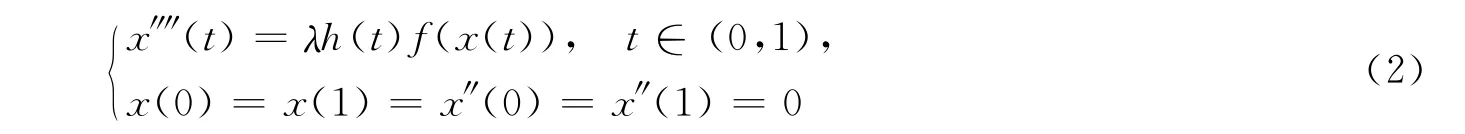
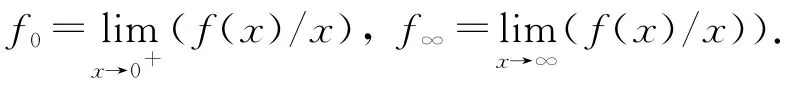
本文总假设:
(H1)f:[0,1]×[0,+∞)→ℝ连续,且对任意的t∈(0,1),f(t,0)<0;
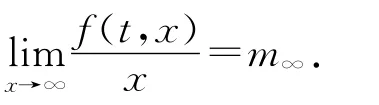
由文献[16]知,线性特征值问题
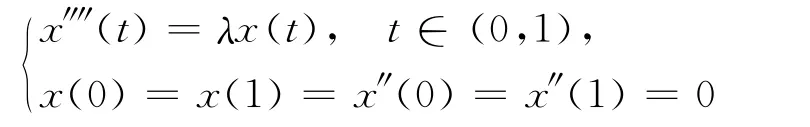
有主特征值λ1>0,及对任意的t∈(0,1),其相应的特征函数φ1(t)>0,且‖φ1‖=1(其中‖·‖为最大模范数).
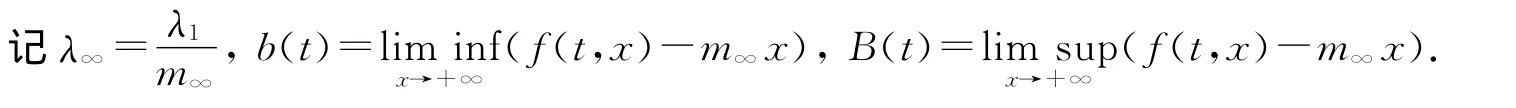
本文的主要结果如下:
定理1 假设(H1),(H2)成立,若存在ε>0,使得下列两种情形之一成立:
1)对任意的t∈(0,1),b(t)>0且λ∈[λ∞-ε,λ∞);
2)对任意的t∈(0,1),B(t)<0且λ∈(λ∞,λ∞+ε].
则问题(1)至少存在一个正解.
注1 定理1可以确定λ在λ∞两侧正解无界连通分支的走向.
1 预备知识
引理1[5]若h∈C[0,1],则问题
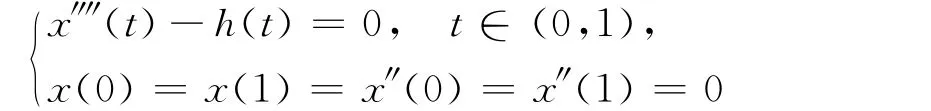
有唯一解x∈C4[0,1],且
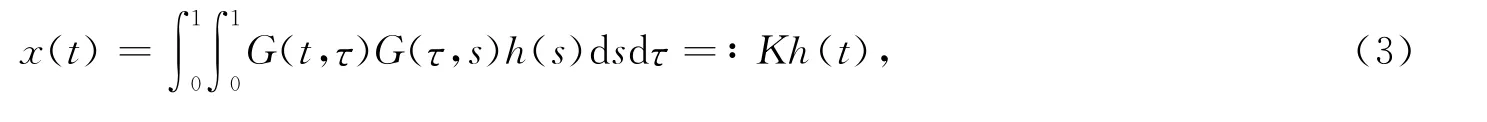
其中G(t,s)是边值问题
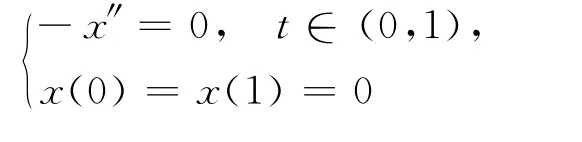
的Green函数,即
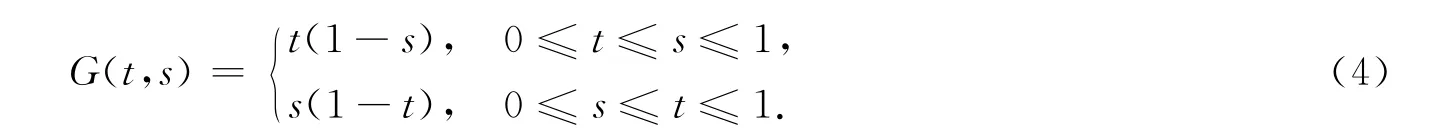
定义线性算子L:D(L)⊂X→X,
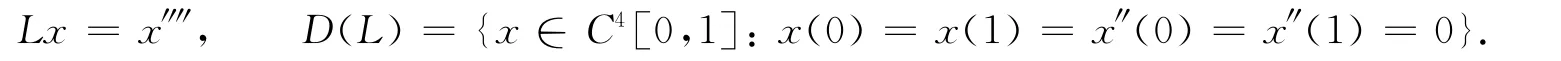
不难验证K∶=L-1:X→X是紧的.
由引理1知,问题(1)等价于
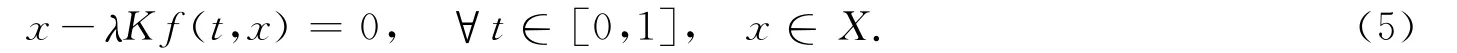
若存在(μn,xn)∈ℝ×X,使得(μn,xn)满足式(5),且μn→λ∞,‖xn‖→∞,则称(λ∞,∞)为问题(5)无穷远处的分歧点.
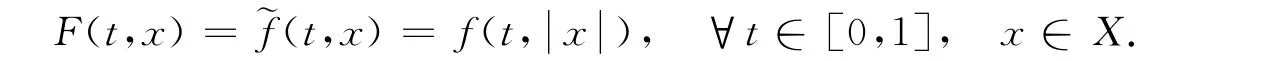
不妨将F(t,x)简记为F(x),对任意的x∈X,定义算子Φ为
显然,对于任意给定的x>0,若Φ(λ,x)=0成立,则x是问题(1)的正解.
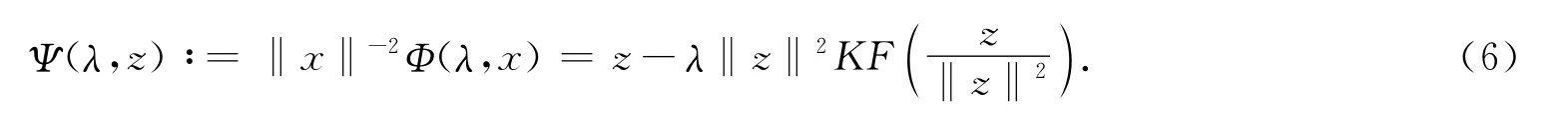
因此,(λ∞,∞)是问题(5)的从无穷远处产生的分歧点,当且仅当(λ∞,0)是Ψ(λ,·)=0从平凡解线上发出的分歧点.
对于任意的r>0,令
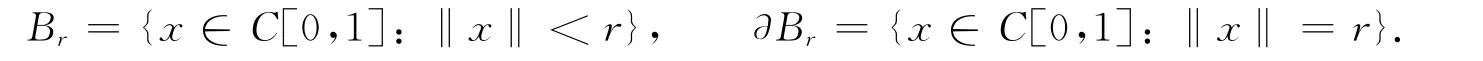
记deg(Ψ(λ,·),Br,0)为 Ψ(λ,·)在 Br上关于0的 Leray-Schauder度;记i(Φ(λ,·),x0,0)为Ψ(λ,·)=0在零点x0处的指数.为方便,记iλ(0)∶=deg(Ψ(λ,·),Br,0).
引理2[17]设Ω为Banach空间E的开子集,f=I-F:¯Ω→E是全连续场,若存在e0∈E,e0≠θ,使得f(x)≠τe0(∀τ≥0,∀x∈∂Ω),则必有deg(f,Ω,θ)=0.
2 主要结果的证明
引理3 对于任意的紧区间Λ⊂[0,+∞)\{λ∞}及任意的λ∈Λ,存在r>0,使得若‖x‖≥r,则Φ(λ,x)≠0.进一步:
1)若对任意的t∈[0,1],b(t)>0,则可取Λ=[λ∞,λ],∀λ>λ∞;
2)若对任意的t∈[0,1],B(t)<0,则可取Λ=[0,λ∞].
证明:反设存在μn→μ≥0,μ≠λ∞,使得当‖xn‖→∞时,xn=μnKF(xn).
令vn=xn‖xn‖-1,则
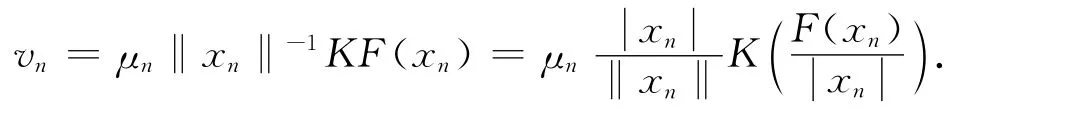
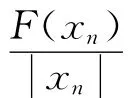
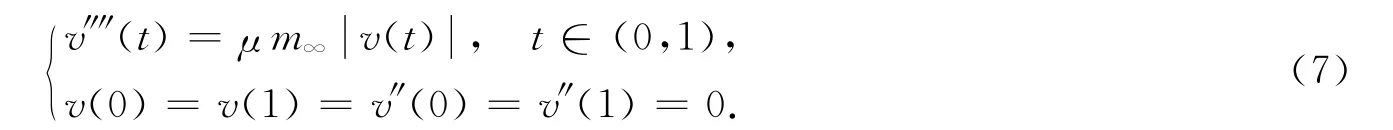
由式(7)知,对任意的t∈[0,1]有v″″(t)≥0.因此v″图像在[0,1]下凸,结合边界v″(0)=v″(1)=0,则

由式(8)及边界v(0)=v(1)=0可得
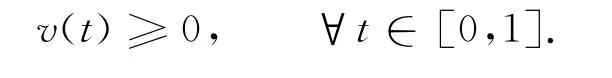
又‖v‖=1,故Lv=μm∞v,于是λ1=μm∞,即μ=λ∞,与假设矛盾.
下面证明1)成立,2)的情形类似可证.取点列{μn}单调递减,且μn→λ∞,n→∞.令v≥0满足
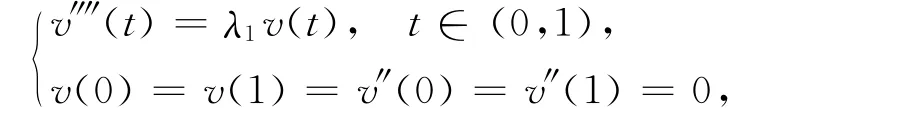
则存在η>0,使得v=ηφ1.
对任意的t∈(0,1),当n充分大时,xn=‖xn‖vn→+∞及F(t,xn)=f(t,xn).由Φ(μn,xn)=0可得
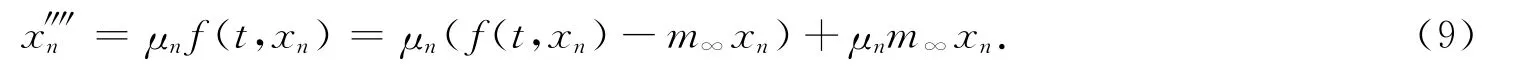
对式(9)两边同时乘以φ1并从0到1积分,再结合φ″″1=λ1φ1可得
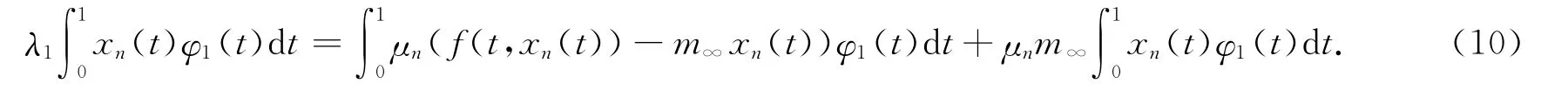
又因μn>λ∞,结合式(10)及Fatou引理可知
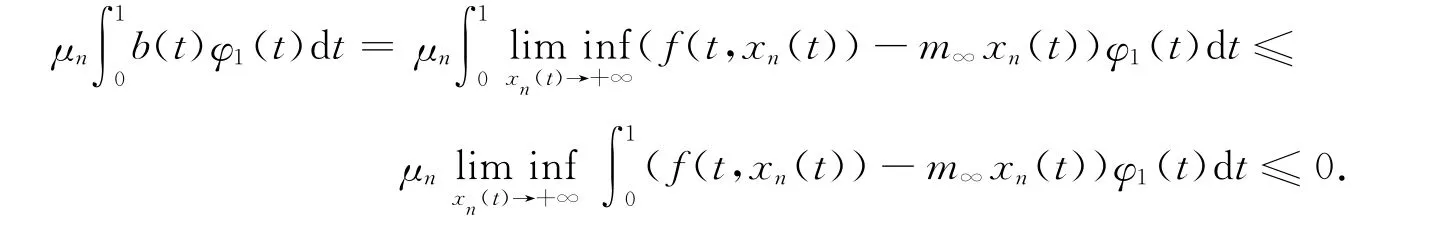
从而与b(t)>0矛盾,故1)成立.
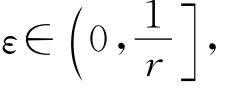
证明:由引理3,取Λ=[0,λ∞],存在r>0,使得对任意的τ∈[0,1],有
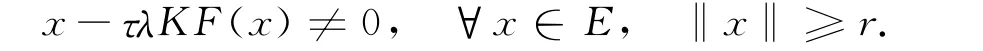
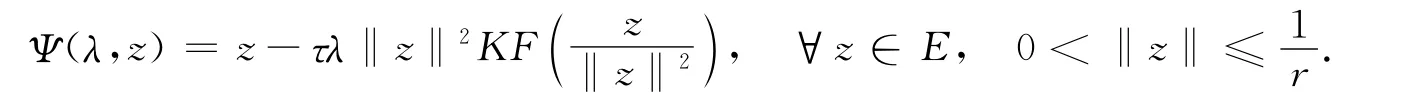
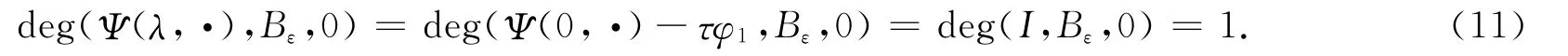
引理4 对任意的λ∈(λ∞,+∞),存在r>0,使得

证明:反设存在τn>0,使得当‖xn‖→∞时,Φ(λ,x)=τnφ1成立,从而

式(12)等价于下列边值问题:
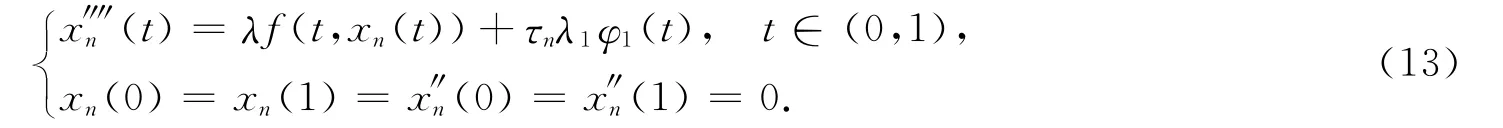
又因φ1为问题(1)的第一主特征值λ1对应的特征函数,即φ1满足
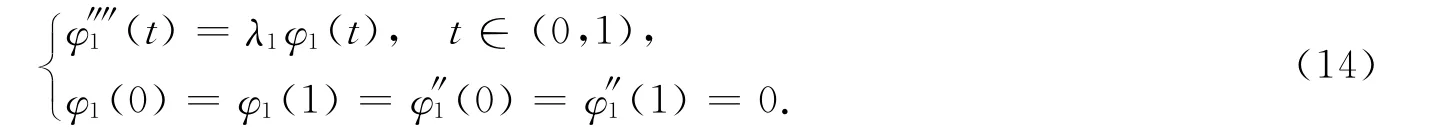
故将式(13)×φ1-式(14)×xn,再从0到1积分得
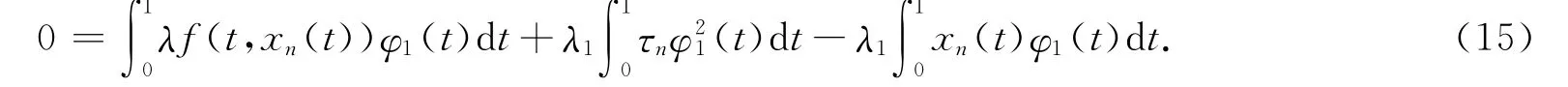
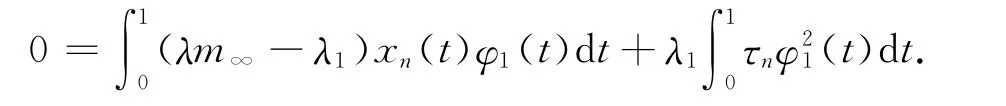
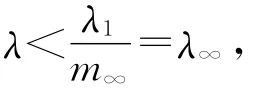
推论2 对任意的λ∈(λ∞,+∞)及ε∈(0,1/r],有deg(Ψ(λ,·),Bε,0)=0.
证明:由引理4可知,存在r>0,使得Φ(λ,x)≠τ‖x‖2φ1,即对任意的τ∈[0,1],x∈E,当‖x‖>r时,有
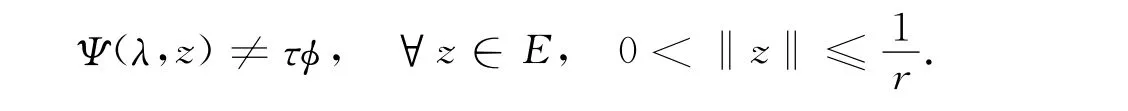
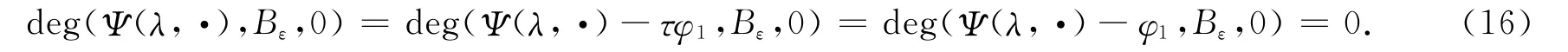
令Σ={(λ,x)∈[0,+∞)×X:x≠0,Φ(λ,x)=0}.
引理5 (λ∞,∞)是问题(5)从无穷远处发出的分歧点,即存在从无穷远处发出的无界闭连通分支Σ∞⊂Σ.进一步,若b>0,则Σ∞向左分歧;若B<0,则Σ∞向右分歧.
证明:结合式(11),(16)可知,存在ε0>0,使得对任意的λ∈(λ∞-ε0,λ∞+ε0),有iλ∞+ε(0)≠iλ∞-ε(0),∀ε∈(0,ε0).于是(λ∞,0)是Ψ(λ,x)=0从平凡解线上产生的一个分歧点.进一步,结合引理3及文献[18]中定理1.3知,当b>0时,Σ∞向左分歧;当B<0时,Σ∞向右分歧.
下面证明定理1.结合上述引理及推论,若当n充分大时,μn→λ∞,‖xn‖→∞,则对任意的t∈(0,1),xn>0.
注2 定理1的证明表明,存在k>0,使得对任意的(λ,x)∈Σ∞,若‖x‖≥k,则有x>0在X中,因此(λ,x)是问题(1)的解.
3 应 用
例1 考虑四阶半正边值问题:
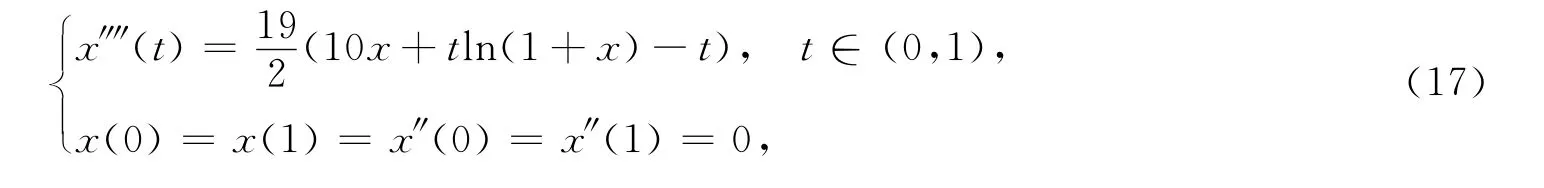
例2 考虑四阶半正边值问题:
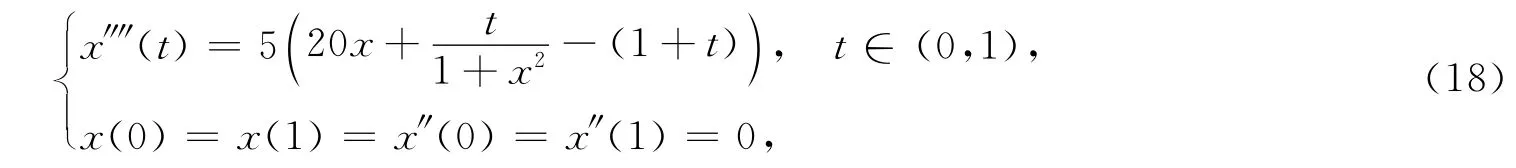
[1]Aftabizadeh A R.Existence and Uniqueness Theoroms for Fourth-Order Boundary Value Problems[J].J Math Anal Appl,1986,116(2):415-426.
[2]Agarwal R P.On Fourthorder Boundary Value Problems Arising in Beam Analysis[J].Differential and Integral Eqautions,1989,2(1):91-110.
[3]MA Ruyun,WANG Haiyan.On the Existence of Positive Solutions of Fourth-Order Ordinary Differential Equations[J].Appl Anal,1995,59(1/2/3/4):225-231.
[4]姚庆六,白占兵.u(4)-λh(t)f(u(t))=0的边值问题的正解存在性 [J].数学年刊:A 辑,1999,20(5):575-578.(YAO Qingliu,BAI Zhanbing.Existence of Solutions of Boundary Value Problems for Fourth-Order Ordinary Differential Equations[J].Chinese Ann Math:Ser A,1999,20(5):575-578.)
[5]BAI Zhanbing,WANG Haiyan.On Positive Solutions of Some Nonlinear Fourth-Order Beam Equations[J].J Math Anal Appl,2002,270(2):357-368.
[6]BAI Zhanbing.The Upper and Lower Solution Method for Some Fourth-Order Boundary Value Problems[J].Nonlinear Anal:Theory Methods & Applications,2007,67(6):1704-1709.
[7]Cabada A,Cid JÁ,Sanchez L.Positivity and Lower and Upper Solutions for Fourthorder Boundary Value Problem [J].Nonlinear Anal:Theory Methods & Applications,2007,67(5):1599-1612.
[8]LIANG Sihua,ZHANG Jihui.The Method of Lower and Upper Solutions for 2n-th-Order Multi-point Boundary Value Problems[J].Nonlinear Anal:Theory Methods & Applications,2009,71(10):4581-4587.
[9]YAO Qingliu.Local Existence of Multiple Positive Solutions to a Singular Cantilever Beam Equation[J].J Math Anal Appl,2010,363(1):138-154.
[10]LI Yongxiang.A Monotone Iterative Technique for Solving the Bending Elastic Beam Equations[J].Appl Math Comput,2010,217(5):2200-2208.
[11]MA Ruyun,XU Ling.Existence of Positive Solutions of a Nonlinear Fourth-Order Boundary Value Problems[J].Appl Math Lett,2010,23(5):537-543.
[12]MA Ruyun,XU Jia.Bifurcation from Interval and Positive Solutions of a Nonlinear Fourth-Order Boundary Value Problem [J].Nonlinear Anal:Theory Methods & Applications,2010,72(1):113-122.
[13]ZHAI Chengbo,YANG Cheng.Multiple Positive Solutions for Semi-positone m-Point Boundary Value Problems[J].Acta Math Appl Sin:Engl Ser,2011,27(3):419-426.
[14]Aris R.Introduction to the Analysis of Chemical Reactors[M].New Jersey:Prentice-Hall Inc,1965.
[15]Webb J R U,Infante G.Semi-positone Nonlocal Boundary Value Problems of Arbitrary Order[J].Commun Pure Appl Anal,2010,9(2):563-581.
[16]徐登洲,马如云.线性常微分方程的非线性扰动 [M].2版.北京:科学出版社,2008.(XU Dengzhou,MA Ruyun.Nonlinear Perturbations of Linear Ordinary Differential Equations[M].2nd ed.Beijing:Science Press,2008.)
[17]郭大钧.非线性泛函分析 [M].2版.济南:山东科学技术出版社,2001.(GUO Dajun.Nonlinear Functional Analysis[M].2nd ed.Jinan:Shandong Science and Technology Press,2001.)
[18]Rabinowitz P H.Some Global Results for Nonlinear Eigenvalue Problems [J].J Funct Anal,1971,7(3):487-513.

