THE SUFFICIENT EFFICIENCY CONDITIONS IN SEMIINFINITE MULTIOBJECTIVE FRACTIONAL PROGRAMMING UNDER HIGHER ORDER EXPONENTIAL TYPE HYBRID TYPE INVEXITIES∗
Department of Mathematics,Texas State University,San Marcos,TX 78666,USA
E-mail:r v124@txstate.edu
THE SUFFICIENT EFFICIENCY CONDITIONS IN SEMIINFINITE MULTIOBJECTIVE FRACTIONAL PROGRAMMING UNDER HIGHER ORDER EXPONENTIAL TYPE HYBRID TYPE INVEXITIES∗
Ram U.VERMA
Department of Mathematics,Texas State University,San Marcos,TX 78666,USA
E-mail:r v124@txstate.edu
First,a class of higher order exponential type hybrid(α,β,γ,η,ρ,h(·,·),κ(·,·), ω(·,·,·),ϖ(·,·,·),θ)-invexities is introduced,second,some parametrically sufcient efciency conditions based on the higher order exponential type hybrid invexities are established,and fnally some parametrically sufcient efciency results under the higher order exponential type hybrid(α,β,γ,η,ρ,h(·,·),κ(·,·),ω(·,·,·),ϖ(·,·,·),θ)-invexities are investigated to the context of solving semiinfnite multiobjective fractional programming problems.The notions of the higher order exponential type hybrid(α,β,γ,η,ρ,h(·,·),κ(·,·),ω(·,·,·),ϖ(·,·,·), θ)-invexities encompass most of the generalized invexities in the literature.To the best of our knowledge,the results on semiinfnite multiobjective fractional programming problems established in this communication are new and application-oriented toward multitime multiobjectve problems as well as multiobjective control problems.
semiinfnite fractional programming;multiobjective fractional programming, Hanson-Antczak-type generalized HA(α,β,γ,η,ρ,θ)-V-invex functions;hybrid(α,β,γ,η,ρ,h(·,·),κ(·,·),ω(·,·,·),ϖ(·,·,·),θ)-invexity2010 MR Subject Classifcation90C29;90C30;90C32;90C34;90C46
1 Introduction
Recently,Zalmai[52]introduced the Hanson-Antczak-type generalized(α,β,γ,η,ρ,θ)-V-invexities based on the class of V-r-invex functions defned by Antczak[1],and applying these new functions,established a number of parametric sufcient efciency results under various Hanson-Antczak-type generalized(α,β,γ,ρ,η,θ)-V-invexity frameworks for the semiinfnite multiobjective fractional programming problems.Verma[40,41]has investigated some results on the multiobjective fractional programming based on new∈-efciency conditions,and secondorder(Φ,η,ρ,θ)-invexities for parameter-free∈-efciency conditions.On the other hand, Pitea and Postolache[35-37],motivated by the signifcant applications to mechanical engineering(where curvilinear integral type objectives are extensively applied due to their physical meaning as mechanical work),introduced a new class of multitime multiobjective variationalproblems of minimizing a vector of functionals of curvilinear integral type,and applied to establish certain new conditions for Mond-Weir-Zalmai type duality for multitime multiobjective variational problems using the notion of the(ρ,b)-quasiinvexity.The curvilinear integral type objectives play an essential role in mathematical modeling of certain processes relating to robotics,tribology,and others.This is equivalent to stating that for a given number of r sources producing mechanical work,minimize r on a set of limited resources.There are also accelerated advances investigating duality for a class of multiobjective control problems based on the generalized invexity by Liang and Ye[55],Mond and Smart[32],Bhatia and Kumar [4],where the objective functionals and constraint functionals are diferent as well as the same. Liang and Ye[55]have applied duality models to more generalized aspects for the Mond-Smart generalized invexity[32]to the context of scalar control problems.Verma[42]established a class of results for multiobjective fractional subset programming problems as well.
Next,we introduce the diferentiable functions h,κ:Rn×Rn→Rn,and ω,ϖ:Rn×Rn× Rn→Rn,which are crucial to the higher order exponential type hybrid(α,β,γ,η,ρ,h(·,·), κ(·,·),ω(·,·,·),ϖ(·,·,·),θ)-invexity framework.Based on this new framework for the higher order exponential type hybrid(α,β,γ,η,ρ,h(·,·),κ(·,·),ω(·,·,·),ϖ(·,·,·),θ)-invexities,we consider the following semiinfnite multiobjective fractional programming problem:
subject to

We observe that multiobjective programming problems of the form(P)but with a fnite number of constraints(where the functions Gjare independent of t,and the functions Hkare independent of s)have been investigated for the past several decades with several classes of static and dynamic optimization problems with multiple fractional objective functions that have been considered leading to a number of sufcient efciency and duality results currently available in the related literature.In this communication,we intend frst to introduce the higher order exponential type hybrid(α,β,γ,ρ,η,h(·,·),κ(·,·),ω(·,·,·),ϖ(·,·,·),θ)-invexities,and then we formulate a number of parametric sufcient efciency results for the semiinfnite multiobjective fractional programming problem(P)under various generalized higher order exponential type hybrid(α,β,γ,ρ,η,h(·,·),κ(·,·),ω(·,·,·),ϖ(·,·,·),θ)-invexity frameworks.The semiinfnite programming problems(if it has a fnite number of variables and infnitely many constraints)ofer more constructive applications in terms of theoretical as well as concrete,real-world problems,including probability and statistics,engineering design,boundary value problems,defect minimization for operator equations,geometry,random graphs,wavelet analysis,reliability testing,environmental protection planning,semidefnite programming,optimal control problems,and robotics.Problems of this nature have been applied for the modeling and analysis of a wide range of theoretical as well as concrete,real-world,practical problems.Semiinfnite programming concepts and techniques have found relevance and applications in approximation theory,statistical models,game theory,engineering design,boundary value problems,graphs related to Newton fows,wavelet analysis,reliability testing,environmental protection planning, decision making and management,geometric programming,optimal control problems,robotics, and continuum mechanics,among others.For more details,we refer the reader[1-55].
We observe that all the parametrically sufcient efciency results established in this paper can easily be modifed and restated for each one of the following classes of nonlinear programming problems,which are special cases of(P):
where F(assumed to be nonempty)is the feasible set of(P),that is,
subject to

where G is the feasible set of(P4),that is,
The paper begins with an introductory section,while in Section 2,the higher order exponential type hybrid(α,β,γ,η,ρ,h(·,·),κ(·,·),ω(·,·,·),ϖ(·,·,·),θ)-invexities,which generalize HA(α,β,γ,ρ,η,θ)-V-invexities introduced and studied by Zalmai[52],are introduced,whileencompass most of the invexity notions in the literature.In Section 3,we present some sufcient efciency conditions,and prove several sets of sufciency criteria under a variety of the higher order exponential type hybrid(α,β,γ,ρ,η,h(·,·),θ)-invexities that are placed on certain vector-valued functions whose entries consist of the individual as well as some combinations of the problem functions.We also observe that all the parametric sufcient efciency results established in this paper regarding problem(P)can be modifed to several special classes of nonlinear programming problems.Finally,a parametric duality problem to primal problem(P) based on the parametric efciency conditions for(P)is presented.
2 Preliminaries
In this section we frst introduce the notion of the higher order exponential type hybrid (α,β,γ,η,ρ,h(·,·),κ(·,·),ω(·,·,·),ϖ(·,·,·),θ)-invexities,and then recall some other related auxiliary results instrumental to the problem on hand.Recently,Antczak[1]introduced the following variant of the class of V-invex functions.

This class of functions was considered in[1]for establishing some sufciency and duality results for a nonlinear programming problem with diferentiable functions,and their nonsmooth analogs were discussed in[2].Recently,Zalmai[52]introduced the Hanson-Antczak type generalized HA(α,β,γ,η,ρ,θ)-V-invexity,an exponential type framework,and then he applied to a set of problems on fractional programming.As a result,he further envisioned a vast array of interesting and signifcant classes of generalized convex functions.Now inspired by[52],we present higher order exponential type hybrid(α,β,γ,η,ρ,h(·,·),κ(·,·),ω(·,·,·),ϖ(·,·,·), θ)-invexities that generalize and encompass most of the existing notions available in the current literature.Let the function F=(F1,F2,···,Fp):X→Rpbe diferentiable at x∗.

where‖·‖is a norm on Rnand
with h:Rn×Rn→Rndiferentiable.
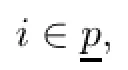

Next,we present some examples for the generalized higher order exponential type(α,β,γ, η,ρ,h(·,·),θ)-invexities.Let the function F=(F1,F2,···,Fp):X→Rpbe diferentiable at x∗.

for α(x,x∗)/=0 and β(x,x∗)/=0 for all x∈X,imples that the function F is(strictly)higher order exponential type hybrid(α,β,η,ω,γ,ξ,ρ,h(·,·),θ)-invex at x∗∈X.
Example 2.6Consider functions f,η and θ defned,respectively,by
Then,for ρ=1 and x<y,we have
Thus,f(x)=ex<ey=f(y)implies that f is strictly(ρ,η,θ)-quasiinvex.
We also observe that for the proofs of the sufcient efciency theorems,sometimes it may be more convenient to apply certain alternative but equivalent forms of the above defnitions based on considering the contrapositive statements.For example,the higher order exponential type hybrid(α,β,γ,η,ρ,h(·,·),θ)-V-quasiinvexity(when α(x,x∗)/=0 and β(x,x∗)/=0 for all x∈X)can be defned in the following equivalent way:

where h:Rn×Rn→Rnis diferentiable.
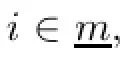
An element x◦∈F is said to be an efcient(Pareto optimal,nondominated,noninferior) solution of(P∗)if there exists no x∈F such that F(x)≤F(x◦).In the feld of multiobjective programming,there exist several versions of the notion of efciency,while most of which are discussed in publications[28,41,48,52].
For the purpose of comparison with the sufcient efciency conditions that will be proposed and discussed in this paper,we next recall a set of necessary efciency conditions for(P).


3 Sufcient Efciency Conditions
In this section,we present several sets of sufciency results in which various generalized higher order exponential type hybrid(α,β,γ,η,ρ,h(·,·),κ(·,·),ω(·,·,·),ϖ(·,·,·),θ)-invexity assumptions are imposed on certain vector functions whose components are the individual as well as some combinations of the problem functions,where h,κ:Rn×Rn→Rn,and ω,ϖ:Rn×Rn×Rn→Rnare diferentiable functions.Let the function εi(·,λ,u):X→R be defned,for fxed λ and u,on a nonempty open convex subset X of Rnby
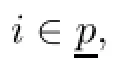
Assume,further that either one of the following two sets of conditions holds:
(a)

Then x∗is an efcient solution of(P).
Proof(a)Based on our assumptions in(i)-(iii),we have

Since γ(x,x∗)>0,even if we consider the both cases α(x,x∗)>0 and α(x,x∗)<0,it follows from the above inequality
Therefore,we conclude that x∗is an efcient solution of(P).
(b)Let x be an arbitrary feasible solution of(P).From(3.1)we observe that
which in view of our(α,β,γ,0,h(·,·),κ(·,·),ω(·,·,·),ϖ(·,·,·),θ)-pseudoinvexity assumption implies that
We need to consider two cases:α(x,x∗)>0 and α(x,x∗)<0.If we assume that α(x,x∗)>0 and recall that γ(x,x∗)>0,then the above inequality becomes
which implies that

Since u∗>0 and ξi(x,x∗)>0,i∈p,the above inequality implies that
which in turn implies that
Since x∈F was arbitrary,we conclude from this inequality that x∗is an efcient solution of (P).On the other hand,we arrive at the same conclusion if we assume that α(x,x∗)<0.?
RemarkWe observe that the proof for Theorem 3.1 can be achieved using the method of contradictions as well.

In addition,assume that any one of the following four sets of hypotheses is satisfed:
(a)
(b)
(c)
(d)
Then x∗is an efcient solution to(P).
Proof(a)Let x be an arbitrary feasible solution to(P).Since Gjm(x,tm)≦0= Gjm(x∗,tm),it follows that
and so
Similarly,assumptions in(iii)lead to the following inequality:
Now combining(3.1),(3.7),and(3.8),and using(iv),we obtain
which in view of(i)implies that
Since¯γ(x,x∗)>0 and φ(x∗)=λ∗,this inequality implies that
Based on the proof of Theorem 3.1,we conclude that x∗is an efcient solution to(P).
(b)-(e)The proofs are similar to that of part(a).?
Now we briefy discuss some modifcations of Theorems 3.1 and 3.3 based on replacing(3.1) with an inequality.

where β:X×X→R and z∈Rn.Furthermore,assume that either one of the two sets of conditions specifed in Theorem 3.1 is satisfed.Then x∗is an efcient solution of(P).
We observe that any solution of(3.1)is also a solution of(3.9),but the converse may not be true.We also observe that Theorem 3.2 generalizes a result of Zalmai([53],Theorem 4.1) on the sufcient efciency conditions.

(a)
(b)
(c)
(d)
Then x∗is an efcient solution of(P).
Next,we present the dual problem(DI)to primal problem(P)based on the parametric efciency conditions for(P)as follows:
(DI)Maximize λ=(λ1,···,λp)
subject to
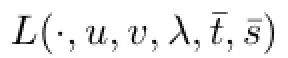
is higher order exponential type hybrid(α,β,γ,η,h(·,·),κ(·,·),ω(·,·,·),ϖ(·,·,·),ρ,θ)-pseudoinvex at y for γ(x,y)>0,where
Then from the pseudoinvexity assumption and(3.10),it follows that
If we assume that α(x,y)>0(while we arrive at the same conclusion for α(x,y)<0)and γ(x,y)>0,then we have
This implies

Since u>0,i∈p,it further follows that
which in turn implies that
This results in φ(x)≰λ,that is,(DI)is a dual problem to(P).
Furthermore,the dual problem(DI)generalizes most of duality models,especially to the context of semiinfnite multiobjective fractional programming problems.
4 Concluding Remarks

Furthermore,based on the new class of multitime multiobjective variational problems for duality theorems(introduced and investigated by Pitea and Postolache[35-37]),we observe that our results can be applied to this class of multitime multiobjective variational problems. It seems that the work of Pitea and Postolache[35-37]on multitime multiobjective variational problems ofer greater opportunities for further future research endeavors based on other aspects of generalized invexities.On the other hand,there is also a greater scope for further research advances for applying the Mond-Smart generalized invexities for multiobjective control problems relating to duality as well as other aspects of the generalized invexities.Liang and Ye[55]investigated duality models for a class of multiobjective control problems based on the generalized invexity.
[1]Antczak T.The notion of V-r-invexity in diferentiable multiobjective programming.J Appl Anal,2005, 11:63-79
[2]Antczak T.Optimality and duality for nonsmooth multiobjective programming problems with V-r-invexity. J Global Optim,2009,45:319-334
[3]Ben-Israel A,Mond B.What is invexity?J Austral Math Soc Ser B,1986,28:1-9
[4]Bhatia D,Kumar P.Multiobjective control problem with generalized invexity.J Math Anal Appl,1995, 189:676-692
[5]Chen H,Hu C F.On the resolution of the Vasicek-type interest rate model.Optimization,2009,58:809-822
[6]Craven B D.Invex functions and constrained local minima.Bull Austral Math Soc,1981,24:357-366
[7]Daum S,Werner R.A novel feasible discretization method for linear semi-infnite programming applied to basket option pricing.Optimization,2011,60:1379-1398
[8]Ergen¸c T,Pickl S W,Radde N,Weber G-W.Generalized semi-infnite optimization and anticipatory systems.Int J Comput Anticipatory Syst,2004,15:3-30
[9]Fiacco A V,Kortanek K O,eds.Semi-infnite Programming and Applications.Lecture Notes in Economics and Mathematical Systems,Vol 215.Berlin:Springer,1983
[10]Giorgi G,Guerraggio A.Various types of nonsmooth invex functions.J Inform Optim Sci,1996,17:137-150
[11]Giorgi G,Mititelu S¸t.Convexit´es g´en´eralis´ees et propri´et´es.Rev Roumaine Math Pures Appl,1993,38: 125-172
[12]GlashofK,Gustafson S A.Linear Optimization and Approximation.Berlin:Springer,1983
[13]Goberna M A,L´opez M A.Linear Semi-Infnite Optimization.New York:Wiley,1998
[14]Goberna M A,L´opez M A,eds.Semi-infnite Programming-Recent Advances.Dordrecht:Kluwer,2001
[15]Gribik P R.Selected applications of semi-infnite programming//Cofman C V,Fix G J,eds.Constructive Approaches to Mathematical Models.New York:Academic Press,1979:171-187
[16]Gustafson S A,Kortanek K O.Semi-infnite programming and applications//Bachem A,et al,eds.Mathematical Programming:The State of the Art.Berlin:Springer,1983:132-157
[17]Hanson M A.On sufciency of the Kuhn-Tucker conditions.J Math Anal Appl,1981,80:545-550
[18]Hanson M A,Mond B.Further generalizations of convexity in mathematical programming.J Inform Optim Sci,1982,3:25-32
[19]Henn R,Kischka P.¨Uber einige Anwendungen der semi-infniten Optimierung.Zeitschrift Oper Res,1976, 20:39-58
[20]Hettich R,ed.Semi-infnite Programming,Lecture Notes in Control and Information Sciences,Vol 7.Berlin: Springer,1976
[21]Hettich R,Kortanek K O.Semi-infnite programming:theory,methods,and applications.SIAM Review, 1993,35:380-429
[22]Hettich R,Zencke P.Numerische Methoden der Approximation und Semi-infnite Optimierung.Stuttgart: Teubner,1982
[23]Jess A,Jongen H Th,Nerali´c,Stein O.A semi-infnite programming model in data envelopment analysis. Optimization,2001,49:369-385
[24]Jeyakumar V,Mond B.On generalised convex mathematical programming.J Austral Math Soc Ser B, 1992,34:43-53
[25]Kanniappan P,Pandian P.On generalized convex functions in optimization theory-A survey.Opsearch, 1996,33:174-185
[26]L´opez M,Still G.Semi-infnite programming.European J Oper Res,2007,180:491-518
[27]Martin D H.The essence of invexity.J Optim Theory Appl,1985,47:65-76
[28]Miettinen K M.Nonlinear Multiobjective Optimization.Boston:Kluwer Academic Publishers,1999
[29]Mititelu S¸t.Invex functions.Rev Roumaine Math Pures Appl,2004,49:529-544
[30]Mititelu S¸t.Invex sets and nonsmooth invex functions.Rev Roumaine Math Pures Appl,2007,52:665-672
[31]Mititelu S¸t,Postolachi M.Nonsmooth invex functions via upper directional derivative of Dini.J Adv Math Stud,2011,4:57-76
[32]Mond B,Smart I.Duality and sufciency in control problems with invexity.J Math Anal Appl,1988,136: 325-333
[33]Mond B,Weir T.Generalized concavity and duality//Schaible S,Ziemba W T,eds.Generalized Concavity in Optimization and Economics.New York:Academic Press,1981:263-279
[34]Nerali´c L,Stein O.On regular and parametric data envelopment analysis.Math Methods Oper Res,2004, 60:15-28
[35]Pitea A,Postolache M.Duality theorems for a new class of multitime multiobjective variational problems. J Global Optimization,2012,54(1):47-58
[36]Pitea A,Postolache M.Minimization of vectors of curvilinear functionals on the second order jet bundle: Necessary conditions.Optimization Letters,2012,6(3):459-470
[37]Pitea A,Postolache M.Minimization of vectors of curvilinear functionals on the second order jet bundle: Sufcient efciency conditions.Optimization Letters,2012,6(8):1657-1669
[38]Sawaragi Y,Nakayama H,Tanino T.Theory of Multiobjective Optimization.New York:Academic Press, 1986
[39]Stein O.Bilevel Strategies in Semi-infnite Programming.Boston:Kluwer,2003
[40]Verma R U.Weak∈-efciency conditions for multiobjective fractional programming.Appl Math Comput, 2013,219:6819-6827
[41]Verma R U.Second-order(Φ,η,ρ,θ)-invexities and parameter-free∈-efciency conditions for multiobjective discrete minmax fractional programming problems.Adv Nonlinear Variational Inequalities,2014,17(1): 27-46
[42]Verma R U.New∈-optimality conditions for multiobjective fractional subset programming problems.Trans Math Prog Appl,2013,1(1):69-89
[43]Verma R U.Parametric duality models for multiobjective fractional programming based on new generation hybrid invexities.J Appl Funct Anal,2015,10(3/4):234-253
[44]Verma R U.Multiobjective fractional programming problems and second order generalized hybrid invexity frameworks.Statistics,Optimization&Information Computing,2014,2(4):280-304
[45]Weber G-W.Generalized semi-infnite optimization:theory and applications in optimal control and discrete optimization.J Stat Manag Syst,2002,5:359-388
[46]Weber G-W,Tezel A.On generalized semi-infnite optimization of genetic networks.TOP,2007,15:65-77
[47]Weber G-W,Tezel A,Taylan P,S¨oyler A,C¸etin M.Mathematical contributions to dynamics and optimization of gene-environment networks.Optimization,2008,57:353-377
[48]White D J.Optimality and Efciency.New York:Wiley,1982
[49]Winterfeld A.Application of general semi-infnite programming to lapidary cutting problems.European J Oper Res,2008,191:838-854
[50]Yu P L.Multiple-Criteria Decision Making:Concepts,Techniques,and Extensions.New York:Plenum Press,1985
[51]Zalmai G J.Proper efciency principles and duality models for a class of continuous-time multiobjective fractional programming problems with operator constraints.J Stat Manag Syst,1998,1:11-59
[52]Zalmai G J.Hanson-Antczak-type generalized(α,β,γ,ξ,η,ρ,θ)-V-invex functions in semiinfnite multiobjective fractional programming,Part III:Second order parametric duality models.Adv Nonlinear Variational Inequalities,2013,16(2):91-126
[53]Zalmai G J.Hanson-Antczak-type generalized(α,β,γ,ξ,η,ρ,θ)-V-invex functions in semiinfnite multiobjective fractional programming,Part I:Sufcient efciency conditions.Adv Nonlinear Variational Inequalities,2013,16(1):91-114
[54]Zalmai G J.Generalized(F,b,φ,ρ,θ)-univex n-set functions and semiparametric duality models in multiobjective fractional subset programming.Int J Math Math Sci,2005,2005(7):1109-1133
[55]Liang Z A,Ye Q K.Duality for a class of multiobjective control problems with generalized invexity.J Math Anal Appl,2001,256:446-461
∗Received June 30,2014;revised January 5,2015.
 Acta Mathematica Scientia(English Series)2015年6期
Acta Mathematica Scientia(English Series)2015年6期
- Acta Mathematica Scientia(English Series)的其它文章
- REGULARITY FOR A GENERALIZED JEFFREY’S INTEGRAL MODEL FOR VISCOELASTIC FLUIDS∗
- ON A CHARACTERIZATION OF THE S-ESSENTIAL SPECTRA OF THE SUM AND THE PRODUCT OF TWO OPERATORS AND APPLICATION TO A TRANSPORT OPERATOR∗
- CONSENSUS ANALYSIS AND DESIGN OF LINEARINTERCONNECTED MULTI-AGENT SYSTEMS∗
- ITERATIVE REGULARIZATION METHODS FOR NONLINEAR ILL-POSED OPERATOR EQUATIONS WITH M-ACCRETIVE MAPPINGS IN BANACH SPACES∗
- ASYMPTOTIC STABILITY OF TRAVELING WAVES FOR A DISSIPATIVE NONLINEAR EVOLUTION SYSTEM∗
- A MODIFIED TIKHONOV REGULARIZATION METHOD FOR THE CAUCHY PROBLEM OF LAPLACE EQUATION∗
