命题公式的随机真度与推理规则

李修清

LI Xiuqing

桂林航天工业学院 理学部，广西 桂林541004

Faculty of Science,Guilin University of Aerospace Technology,Guilin,Guangxi 541004,China

1 引言

如何将数值计算的思想融入到数理逻辑中来，使以符号化为特点的数理逻辑和以数值求解以及误差估计为特点的数值计算联系起来，从而扩大数理逻辑研究和应用范围，是国内外许多学者长期探讨的课题。早在20世纪50 年代，Rosser 和Turquette 提出了用“指派真值”来反映逻辑公式和逻辑推理的真确度的方法，20 世纪70 年代以来将概率论方法引入数理逻辑的思想已逐步兴起，目前已有“概率逻辑学”专著出版[1]。90 年代以来数理逻辑程度化的研究得到了进一步的发展，取得了许多成果，王国俊教授基于均匀概率思想首先提出了命题逻辑系统中公式的真度概念和逻辑度量空间理论，形成了计量逻辑学[2-6]，它是将数理逻辑与数值计算联系起来的一个新的研究分支，使命题逻辑系统的程度化思想得以实现，但同时也存在随机性不足的缺点。在王国俊教授给出的计量逻辑学里每个原子公式的真度是完全相等的，这就使得如果两个命题公式完全一致，那么它们的真度也一定相等，这种把每个原子公式的真度完全等同看待的观点，显然不符合现实世界中各原子公式成立的概率不尽相同的事实，显然赋予不同原子公式以不同的概率，可以使命题公式的真度更接近于现实世界。基于这样的考虑，惠小静、崔美华等把计量逻辑学与概率逻辑学相结合，就二值和三值逻辑系统提出了随机真度的概念，建立了随机逻辑度量空间理论[7-12]。随机真度既是概率逻辑学中命题公式概率的一般形式，又是计量逻辑学中命题公式真度的一般形式，并且同时克服了两者的缺点，因此对随机真度的性质、特性以及随机度量空间理论的研究，是一项十分有意义的工作。

在二值和三值命题逻辑系统随机化的研究成果上，笔者就n值R0命题逻辑系统和模糊命题逻辑系统，进行了命题公式的随机化研究，建立了随机逻辑度量空间[13]。本文在n值Lukasiewicz 命题逻辑系统中，引入命题公式的随机真度的概念，给出随机真度的一个重要计算公式，研究命题公式随机真度的若干性质，在此基础上证明命题逻辑的分离规则、三段论规则以及交推理规则在n值Lukasiewicz 命题逻辑系统中成立。

2 n 值Lukasiewicz 命题逻辑系统的随机真度

本文引用的概念与符号，若未加说明均参见文献[14-15]，用Ln表示n值Lukasiewicz 命题逻辑系统，蕴含算子取。

设S={q1,q2,…}为原子公式集，F(S)是由S生成的(¬,∨,→)型自由代数，F(S)中的元素称为命题公式或简称为公式。

设A=A(q1,q2,…,qm)∈F(S)是一含有m个原子公式q1,q2,…,qm的命题公式，则A对应一个映射，定义如下：

显然，A所诱导的函数，关于算子¬,∨,→是同态的，即。

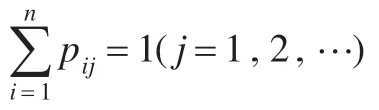
定义2.2[13]设ξ=(ξ1,ξ2,…)是一个n维随机概率分布序列，其中ξ1=(p11,p21,…,pn1)T，ξ2=(p12,p22,…,pn2)T,…,，令φ(α)=φ(x1)×φ(x2)×…×φ(xm)，定义为：当时φ(xi)=pki(k=1,2,…,n;i=1,2,…,m)，则得到一个m维映射，称φ为的一个ξ-随机化映射，简称随机化映射。

为了叙述方便，规定：设Γ是的一个子集，则φ(Γ)=∑{φ(α)|α∈Γ}。

命题2.1[13]设φ为的一个ξ-随机化映射，则，即。

定义2.3设A=A(q1,q2,…,qm)∈F(S)，是A所诱导的函数，ξ=(ξ1,ξ2,…)为一n维随机概率分布序列，φ为上的ξ-随机化映射，令

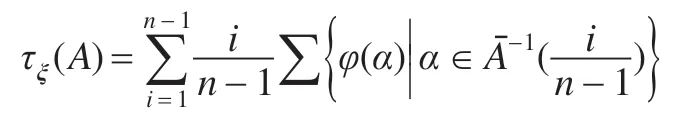
则称τξ(A)为公式A的ξ-随机真度，在不至于引起混淆的情况下，也简称τξ(A)为A的随机真度。

注2.1（i）A的随机真度τξ(A)显然和n维随机概率分布序列ξ=(ξ1,ξ2,…)的取值有关。

（ii）当n=2 时，A的随机真度τξ(A)就是文献[6]中经典命题逻辑中公式的随机真度。

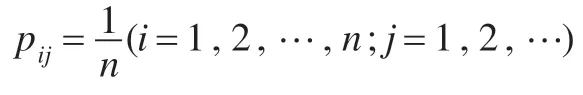
为了对随机真度有一个直观认识，看一个三维，一个四维的例子。

例2.1设，A = q1，B = q1 → q2，ξ = (ξ1, ξ2)，ξ1 = (0.2,0.2,0.6)T，ξ2 = (0.5,0.3,0.2)T为两个独立的三维概率分布，求τξ (A)，τξ (B)。

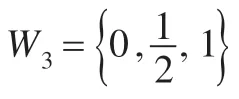
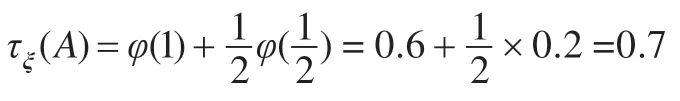
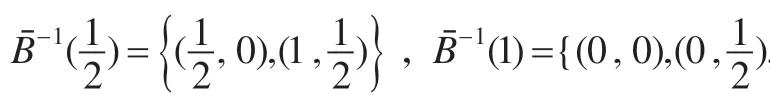
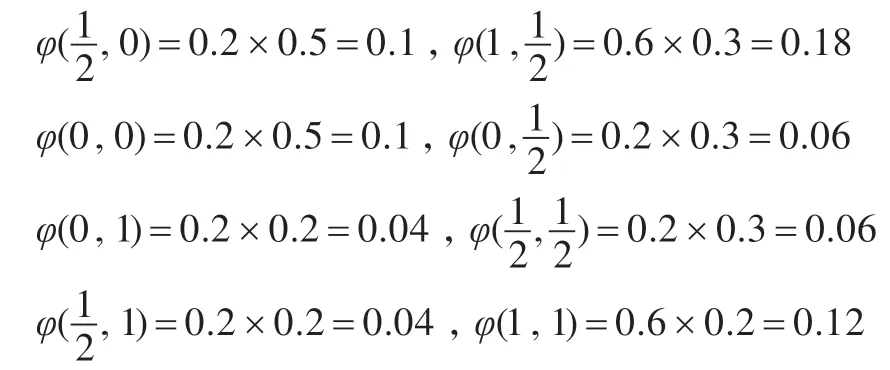
由随机真度计算公式即定义2.3 得：

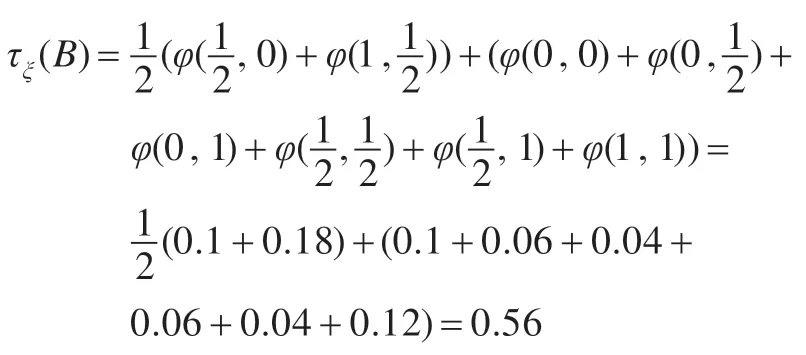
例2.2设A=q1∧q2，ξ=(ξ1,ξ2)，ξ1=(0.1,0.1,0.2,0.6)T，ξ2=(0.2,0.3,0.3,0.2)T为两个独立的四维概率分布，求τξ(A)。

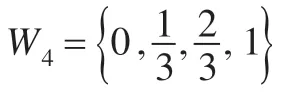
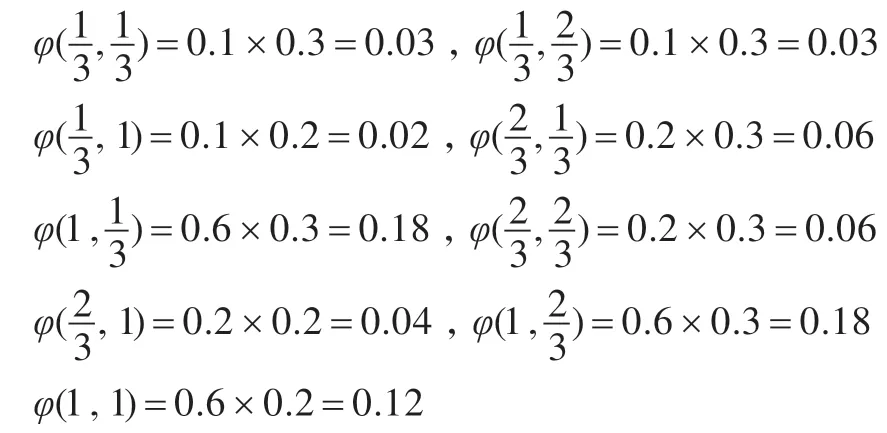
由随机真度计算公式即定义2.3 得：

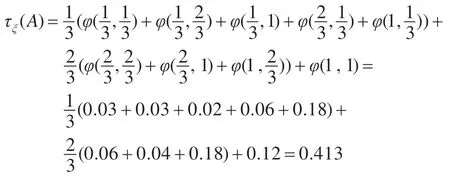
由以上的例子可以看出，随着维数的增加，命题公式随机真度的计算量将会成倍增加，为了简化计算或者合理的估值以及随机度量空间理论等研究的需要，有必要研究随机真度的一些性质。

3 随机真度的性质

为了下面研究的需要，给出定义2.3 所规定的随机真度的一个计算公式。

命题3.1设A=A(q1,q2,…,qm)∈F(S)，是A所诱导的函数，ξ=(ξ1,ξ2,…) 为一n维随机概率分布序列，φ为上的ξ-随机化映射，则τξ(A)=。

证明由ξ-随机真度的定义2.3 得：

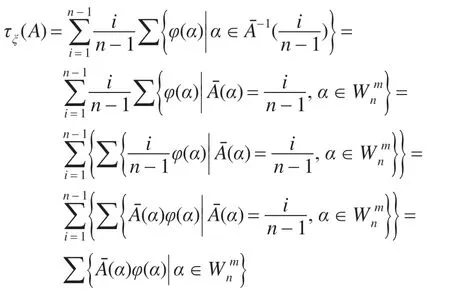
即结论成立。证毕。

定理3.1设A,B∈F(S)，ξ=(ξ1,ξ2,…)为一n维随机概率分布序列，则以下各结论成立：

（i）A是重言式当且仅当τξ(A)=1；A是矛盾式当且仅当τξ(A)=0。

（ii）若A≈B，则τξ(A)=τξ(B)。

（iii）τξ(¬A)=1-τξ(A)。

证明设A、B含有相同的原则公式q1,q2,…,qm，即A=A(q1,q2,…,qm)，B=B(q1,q2,…,qm)。

（i）A是重言式是指，对于，有，于是由随机真度的计算公式命题3.1 得：；反之，若A不是重言式，则，使，则同样由随机真度的计算公式即命题3.1 得：；于是就证明了：A是重言式当且仅当τξ(A)=1。同理可证，A是矛盾式当且仅当τξ(A)=0。

（ii）由A≈B知，对于，有，于是由命题3.1 得：。

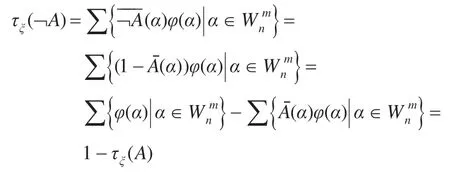
证毕。

定理3.2设A,B∈F(S)，ξ=(ξ1,ξ2,…)为一n维随机概率分布序列，则以下各结论成立：

（i）τξ(A∨B)=τξ(A)+τξ(B)-τξ(A∧B)。

（ii）τξ(A→B)=τξ(A∧B)-τξ(A)+1。

（iii）┣A→B，则τξ(A)≤τξ(B)。

证明设A、B含有相同的原子公式q1,q2,…,qm，即A=A(q1,q2,…,qm)，B=B(q1,q2,…,qm)。

（i）设a,b∈[0,1]，首先证明一个等式a∨b=a+b-(a∧b)对于Lukasiewicz 蕴含算子→成立。就a,b的不同大小分别验证：

情形1若a≤b∈[0,1]，则a∨b=b，a+b-(a∧b)=a+b-a=b，等式成立；

情形2若a＞b∈[0,1]，则a∨b=a，a+b-(a∧b)=a+b-b=a，等式成立；

这样就验证了以上等式成立。

由A、B含有m个相同的原子公式，知A、B的诱导函数都是上的m元函数，即∀α=(x1,x2,…,xm)∈有，，故由以上证明的等式得：

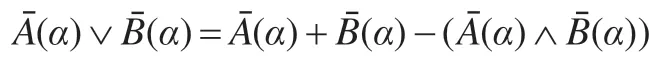
注意到诱导函数的同态性，即

4.坚持激浊扬清。要使党内政治生活正气充沛，就必须树正气、遏邪气，形成正向激励与负向遏制的鲜明导向，对符合党内政治生活规定要求的人和事给予肯定和褒奖，对违背的给予惩处甚至绳之以法。习近平同志提出：“要激浊扬清，坚持激浊和扬清两手抓。”[2]

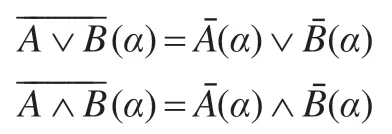
上式变形为：

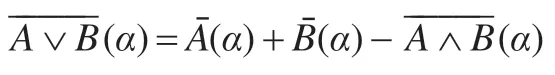
两边乘以定义2.2 给出的随机化映射φ(α)得：

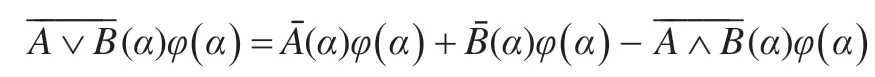
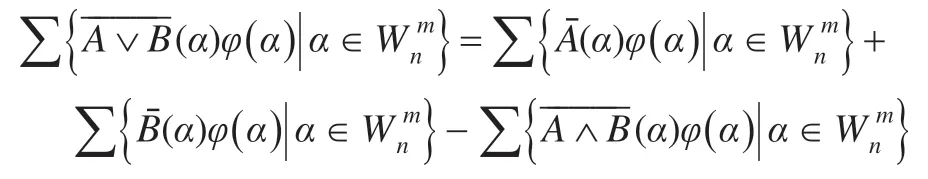
于是由随机真度的计算公式即命题3.1 得：

τξ(A∨B)=τξ(A)+τξ(B)-τξ(A∧B)

（ii）先证明等式：a→b=(a∧b)-a+1 在Wn中关于运算¬,∨,→成立。同样分a、b不同大小情形讨论：

情形1若a≤b∈Wn，则a→b=(1-a+b)∧1=1，(a∧b)-a+1=a-a+1=1，故等式成立；

这样就验证了以上等式成立。

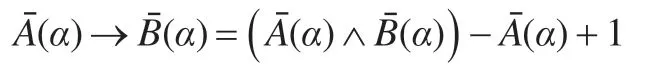
同样注意到诱导函数的同态性，等式可变形为：

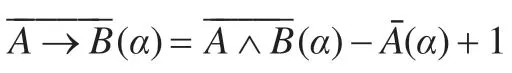
两边乘以随机化映射φ(α)得：

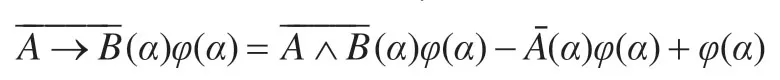
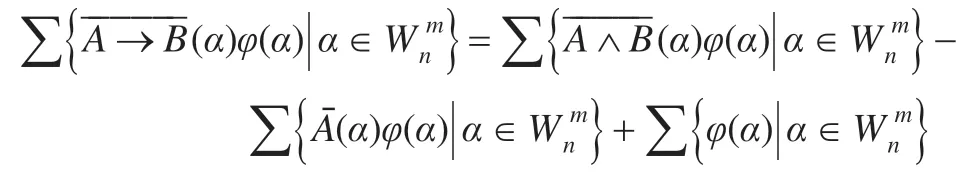
τξ(A→B)=τξ(A∧B)-τξ(A)+1

（iii）由已知┣A→B知A→B是定理，即有，，由算子的同态性得，，于是得有，，同以上证明一样，不等式两边同乘以随机化映射φ(α)，再对中的全体α求和得，即τξ(A)≤τξ(B)。证毕。

推论3.1设A,B∈F(S)，ξ=(ξ1,ξ2,…)为一n维随机概率分布序列，则：

（i）τξ(A∨B)≥max{τξ(A),τξ(B) }。

（ii）τξ(A∧B)≤min{τξ(A),τξ(B) }。

（iii）τξ(A→B)≥τξ(B)。

证明（i）在Lukasiewicz 命题逻辑系统中，A∨B≈(A→B)→B，故τξ(A∨B)=τξ((A→B)→B)，由定理3.2（ii）得：

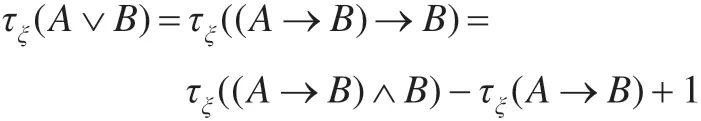
再由定理3.2 的（i）知：

τξ((A→B)∧B)=τξ(A→B)+τξ(B)-τξ((A→B)∨B)

于是得：

同理可证τξ(A∨B)≥τξ(A)，故结论成立。

（ii）和（iii）用类似于（i）的证明方法，同理可证。证毕。

4 随机真度的推理规则

根据随机真度的计算公式以及性质，给出随机真度的推理规则。

定理4.1设A,B,C∈F(S)，α,β∈[0,1]，ξ=(ξ1,ξ2,…)为一n维随机概率分布序列，则：

（i）随机真度的MP 规则，若τξ(A)≥α,τξ(A→B)≥β，则τξ(B)≥α+β-1。

（ii）随机真度的HS规则，若τξ(A→B)≥α,τξ(B→C)≥β，则τξ(A→C)≥α+β-1。

证明不妨设A、B、C含有相同的原子公式q1,q2,…,qm。

（i）先证明一个不等式b≥a+(a→b)-1，a,b∈[0,1]在Wn关于算子¬,∨,→构成的自由代数中成立。

当a≤b∈Wn时，a→b=1，则a+(a→b)-1=a，不等式成立；

当a＞b∈Wn时，a→b=1-a+b，则a+(a→b)-1=a+(1-a+b)-1=b，不等式成立。

故证明了以上给出的不等式成立。

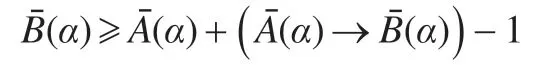
设φ是由定义2.2给出的随机化映射，则0 ＜φ(α)＜1，上式两边乘以φ(α)，再对中的全体α求和得：

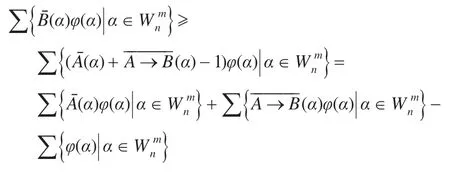
由命题2.1及随机真度的计算公式得：τξ(B)≥τξ(A)+τξ(A→B)-1，注意到已知条件τξ(A)≥α,τξ(A→B)≥β，显然得到结论成立。

（ii）在n值Lukasiewicz命题逻辑系统中，有├(B→C)→((A→B)→(A→C))，即(B→C)→((A→B)→(A→C))是n值Lukasiewicz命题逻辑系统中的定理，由Lukasiewicz命题逻辑系统的完备性[5]知，命题公式(B→C)→((A→B)→(A→C)) 是 重 言 式，于 是 由 定 理3.1 得：τξ((B→C)→((A→B)→(A→C)))=1，已知τξ(B→C)≥β，应用本定理证明的结论（i）得τξ((A→B)→(A→C))≥β；再利用已知条件τξ(A→B)≥α，继续应用本定理的结论（i）得τξ(A→C)≥α+β-1。证毕。

定理4.2随机真度的交推理规则：设A,B,C∈F(S)，α,β∈[0,1]，ξ=(ξ1,ξ2,…)为一n维随机概率分布序列，若τξ(A→B)≥α,τξ(A→C)≥β，则τξ(A→B∧C)≥α+β-1。

证明由定理3.2（ii）得：

τξ(A→(B∧C))=τξ(A∧B∧C)-τξ(A)+1

再由定理3.2 得（i）：

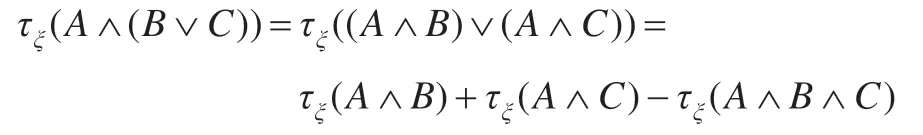
即τξ(A∧B∧C)=τξ(A∧B)+τξ(A∧C)-τξ(A∧(B∨C))。

由推论3.1 知τξ(A∧(B∨C))≤τξ(A)，故得：

τξ(A→B∧C)≥τξ(A∧B)+τξ(A∧C)-2τξ(A)+1

再应用定理3.2 的（ii）得：

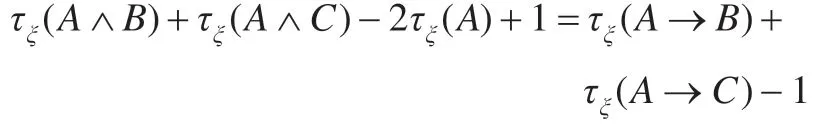
于是得：

τξ(A→B∧C)≥τξ(A→B)+τξ(A→C)-1 ≥α+β-1

证毕。

5 结束语

继计量逻辑学以及二值三值命题逻辑随机化的研究成果，以及在n值R0命题逻辑系统中引入的随机真度概念的基础上，本文在n值Lukasiewicz 命题逻辑系统中引入了命题公式的随机真度概念，给出了随机真度的重要计算公式，利用随机真度的计算公式研究了随机真度的若干性质，证明命题逻辑的分离规则、三段论规则以及交推理规则在n值Lukasiewicz 命题逻辑系统中成立。随机真度的概念和性质还可以推广到赋值域为[0,1]的模糊命题逻辑中，从而可以引出模糊命题逻辑系统随机逻辑度量空间的概念，在随机逻辑度量空间中，可研究理论的相似度、理论的相容度以及近似推理等问题，这些都是十分有意义的工作，将在另文分别阐述。

[1] Adams E W.A primer of probability logic[M].Stanford：CSLI Publications，1998.

[2] Wang G J，Leung Y.Integrated semantics and logic metric spaces[J].Fuzzy Sets and Systems，2003，136（1）：71-91.

[3] 王国俊，李壁镜.Lukasiewiczn值命题逻辑中公式的真度理论和极限定理[J].中国科学：E 辑，2005，35（6）：561-569.

[4] 王国俊，王伟.逻辑度量空间[J].数学学报，2001，44（1）：159-168.

[5] 王国俊.计量逻辑学（I）[J].工程数学学报，2006，23（2）：191-215.

[6] 王国俊，宋建社.命题逻辑中的程度化方法[J].电子学报，2006，34（2）：252-257.

[7] 惠小静，王国俊.经典推理模式的随机化研究及其应用[J].中国科学：E 辑，2007，37（6）：801-812.

[8] 惠小静，王国俊.经典推理模式的随机化研究及其应用（II）[J].模糊系统与数学，2008，22（3）：21-26.

[9] 惠小静.三值R0命题逻辑系统的随机化[J].应用数学学报，2009，32（1）：19-27.

[10] 惠小静，王国俊.D-逻辑度量空间与近似推理[J].南京大学学报数学半年刊，2007，24（2）：249-257.

[11] 惠小静.三种近似推理模式的等价性[J].计算机工程与应用，2008，44（27）：56-57.

[12] 崔美华.逻辑系统L3中公式的随机真度与似推理[J].高校应用数学学报，2010，25（4）：496-502.

[13] 李修清，朱宁.R0型命题逻辑系统的随机化[J].模糊系统与数学，2013，27（1）：63-70.

[14] 王国俊.数理逻辑引论与归结原理[M].2 版.北京：科学出版社，2006.

[15] 王国俊.非经典数理逻辑与近似推理[M].2 版.北京：科学出版社，2008.