二维非均匀空间中气体放电模型的动力学分析
姜 雷,彭 静,袁晓辉
(1.哈尔滨师范大学 数学科学学院,黑龙江 哈尔滨150025;2.东北农业大学 电气与信息工程学院,黑龙江 哈尔滨150030;3.中国科学院 东北地理与农业生态研究所,黑龙江 哈尔滨150040)
孤立子是自然界中一种常见的现象,在气体放电试验[1]、Pt 表面的CO 催化氧化反应等许多物理、化学试验中都可以观察到孤立子运动。从20 世纪60 年代开始,孤立子就引起了研究者的极大兴趣。为解释其背后的数学机理,Gas -Discharge、Gray -Scott 等模型被用来研究孤立子相互碰撞后产生的复杂现象,如反弹、融合和消失等。通过对Gray -Scott 模型孤立子解碰撞的数值解析,NISHIURA[2]等发现分水岭解是控制这些复杂现象变迁的主要因素。分水岭解是一种不稳定的解,当其受到不同方向的扰动时会有不同的变化,如反弹或者穿过、融合或者分裂等。与孤立子之间的碰撞相比,非均匀空间上孤立子的动力学特性研究相对较少。YUAN[3]等研究了一维非均匀空间中Gas-Discharge 模型的孤立子解的特性,随着参数变化,孤立子穿过非均匀空间时会产生反弹、停止和消失等现象。与均匀空间中孤立子的碰撞类似,一维非均匀空间中也存在着一类分水岭解控制着孤立子的状态变迁。NISHIURA[4-5]等模拟了二维空间中孤立子从不同角度与非均匀边界进行碰撞的过程。在二维空间中随着自由度的增加,细微扰动可以使孤立子的轨道发生迁移,从而观察到旋转、分裂等新现象。为了解析二维非均匀空间中孤立子的动力学特性,笔者利用Gas-Discharge 模型模拟了孤立子与非均匀边界正面碰撞的过程,观察到了反射、穿过和分裂等现象的变迁,通过对分水岭解的稳定性解析,解释了这些现象产生的机理。笔者还利用Pseudo Arclength 方法获得了参数空间中解的全局分歧图,阐明了控制不同状态变迁的分水岭解之间的联系。
1 模型与数值模拟方法
气体放电模型(Gas -Discharge)如式(1)所示,最初是由PRUWINS 提出的,用来模拟气体放电实验中观察到的斑图,现在经常被用来研究耗散系统的动力学特性。该模型是一个三变量的反应扩散方程组,其中,变量u是激励子,变量v和w是抑制子。与包含一个激励子和抑制子的双参数反应扩散方程模型(如Gray -Scott 和FitzHugh-Nagumo 模型)不同,Gas - Discharge 模型中第二个抑制子w对二维空间中孤立子的形成起到关键作用。如果在双参数的Gray -Scott 模型中加入一个抑制子,也能获得稳定的孤立子解[6]。
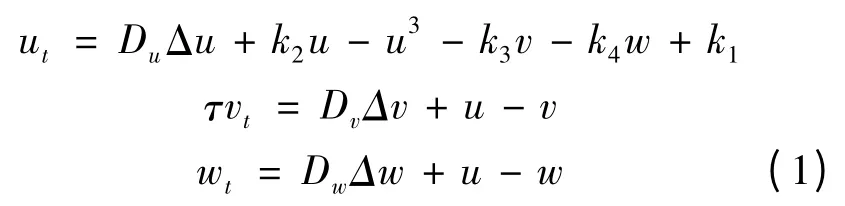
式中:Δ 为拉普拉斯项;u=u(t;r);v=v(t;r);w=w(t;r);r=(x;y)∈R2,k2=2.0;k3=1.0;k4=8.5;τ= 40。扩散系数Du=0.9 ×10-4;Dv=1.0 ×10-3;Dw=1.0 ×10-2。参数k1的值在x方向上按照式(2)所示变化,其中代表左边的k1值,kR1代表右边的k1值,ε=-。
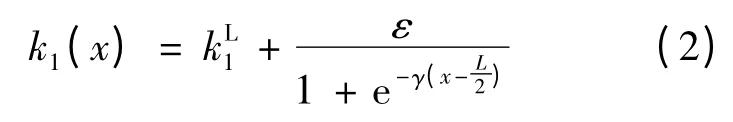
在Gas-Discharge 模型中,非均匀空间模拟示意图如图1 所示,孤立子是一个局部解。在均匀二维空间中,令方程组左边为0,可以得到u=v=w,也就是说二维空间中孤立子解在无限远处时u=v=w。因此,在模拟时可以认为空间中除了孤立子附近区域,其他部分可以看作一个平面。但是在非均匀空间中,k1的值发生变化,也就导致在非均匀边界处u、v、w的值发生变化,形成一个新的解,形状如图1(b)中L/2 附近图1(a)的灰色线条所示,称之为非均匀解(HIOP)。因此,空间足够大时,孤立子在非均匀空间上的动力学分析可以看作是其与HIOP 碰撞的动力学研究。根据NISHIURA 的研究结果,HIOP 解还有其他4种类型[7-8]。
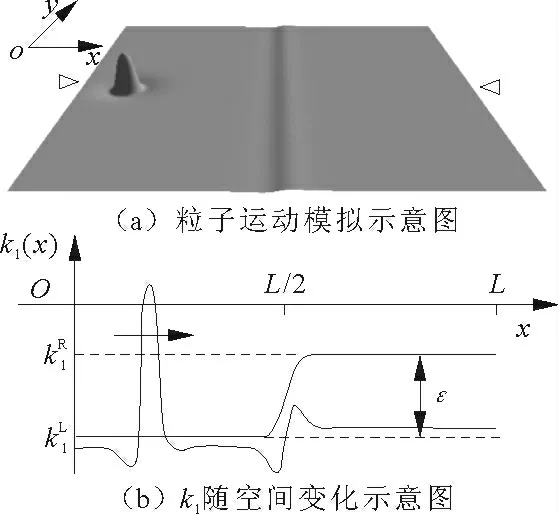
图1 非均匀空间模拟示意图
二维空间中Gas-Discharge 模型的数值计算量较大,笔者根据模型的特点编写了并行分析程序。模型的模拟采用二维Crank -Nicolson 方法。为了获得孤立子和HIOP 的数值解,首先给定一个与HIOP 解非常接近的初值,然后利用Newton- Raphson 迭代法获得精确解。当获得一个HIOP 解后,可以运用Pseudo - Arclength 方法绘制HIOP 解的全局分歧图。由于求解过程中涉及大量矩阵运算,可采用Aztec 软件包将矩阵运算并行化,从而提高程序的运行效率,最后采用Arpack 软件包求解HIOP 解的特征值和特征向量。
2 模拟结果
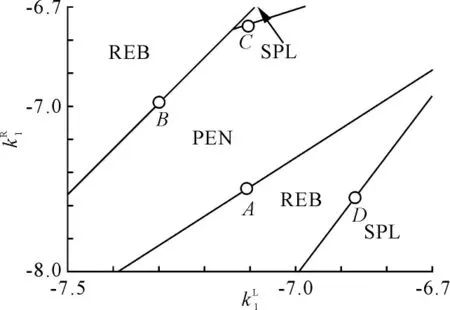
图2 孤立子运动相图
运用上述数值模拟方法,在= (- 7. 5,-6.7),=(-8.0,-6.7)的参数空间中,孤立子与HIOP 碰撞后可以观察到反弹(REB),穿过(PEN),以及分裂(SPL)这3 种现象(如图2 所示)。反弹(REB)是指孤立子从左往右的运行过程中,与HIOP 碰撞以后,改变方向从右向左运动。从图2 中可以看到有两个反弹区域,这两个区域上孤立子返回的位置有所不同,在左上角的反弹区域,孤立子在HIOP 左侧返回;而在右下角的反弹区域,孤立子在HIOP 的右侧返回。这也暗示着相图中反弹(REB)与穿过(PEN)的变迁由两种不同的机制控制。分裂是孤立子与HIOP碰撞后变为两个孤立子沿着HIOP 反向移动。与反弹类似,两个分裂区域分别代表在HIOP 左侧和右侧分裂。在一维非均匀空间中,YUAN 发现分水岭解控制孤立子从反弹到穿过之间的变迁。在二维空间中,是否也存在这样的分水岭解问题,笔者仔细模拟了边界上A、B、C、D点附近孤立子的运动情况。在A点附近(,)≈(-7.10,-7.42),当= -7.423 55 时,孤立子穿过HIOP 到达右侧区域,而当= -7.423 56 时,孤立子与HIOP 碰撞后反弹回左侧区域。从图3 的时间演化图上可以看出,在孤立子决定反弹还是穿过之前,会在一个状态停留一段时间。这似乎存在一个静止的不稳定解,当受到扰动时,其会选择运动方向。利用牛顿迭代法,可以获得该状态的数值解,如图3 所示。这个解与孤立子解不同,首先其速度为0,是一个静止解。其次其与均匀空间中的静止解不同,由于参数的空间非一致性,解在x方向上是不对称的,在y方向上对称。实际上,这个解也是NISHIURA 描述的HIOP 解中的一种。计算该解的特征值可以得到两个大于零的特征值,λ1=7.652 3 ×10-2,λ2=2.635 4 ×10-2,其对应的特征向量如图3 所示,分别对应x方向和y方向。在一维空间中,只能得到一个大于0 的特征值,特征向量也只对应一个方向。将特征向量的值作为扰动加到静止解上,可以看到静止解马上沿着x方向继续前进,表现为穿过,如果将特征向量反向加到静止解上,则会反向运动,表现为反弹。在y方向上特征值作为扰动也会使孤立子沿着y方向正向或反向移动。由于图1 所示的模拟中,孤立子与HIOP 正向碰撞,碰撞过程中在y方向的变形是对称的,因此x方向上的变形对孤立子的运动状态起到主要影响作用。A点附近的HIOP 解在此起到了分水岭解的作用。
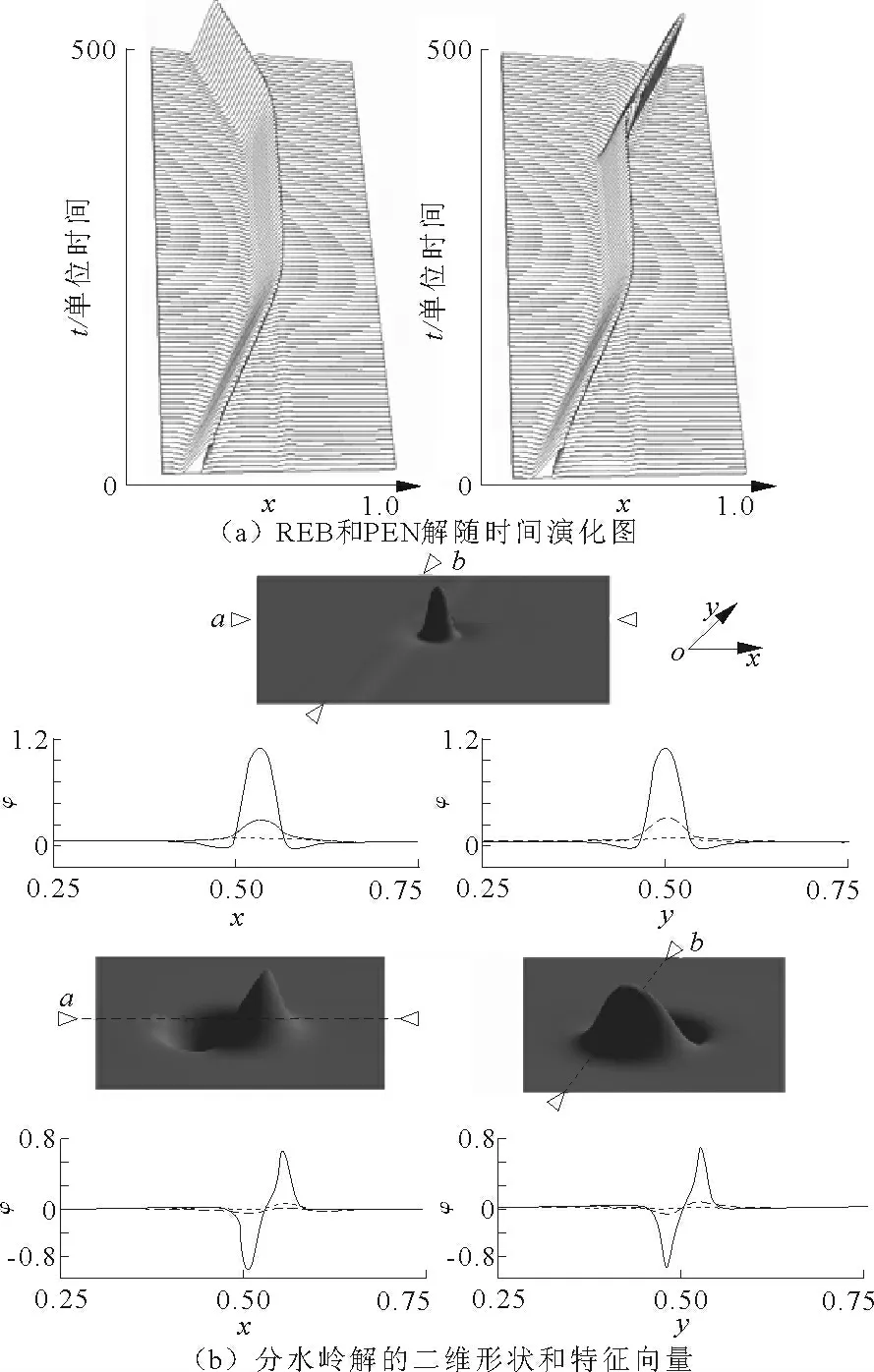
图3 控制REB 和PEN 的分水岭解
在B附近点可以观察到与A点类似的转变,当= -6.985 04时,孤立子穿过HIOP 到达右侧区域,而当=-6.985 03时,孤立子与HIOP 碰撞后反弹回左侧区域。用牛顿迭代法得到一个不稳定解,计算得到该解有两个正的特征值,λ1=9.563 4 ×10-2,λ2=3.678 2 ×10-2,分别对应两个x,y方向的特征向量φ。因此,从上述数值计算可以知道,静止的非稳定解是控制穿过与反弹现象的分水岭解[9-10]。
相图中有两个分裂区域,分裂现象是一维空间没有观察到的新现象。仔细观察穿过与分裂边界上C点附近孤立子的演化发现,如图4 所示,孤立子与HIOP 碰撞后继续前进,碰撞后的孤立子变为一个具有双峰形状的解,而双峰解并不能稳定地继续前进,当= -6.757 170 311 时,双峰解变为两个沿着y方向反向运动的孤立子,当= -6.757 170 312时,双峰解变为一个沿着x方向继续前进的孤立子。利用牛顿迭代法可以得到一个不稳定的双峰解,有一个大于0 的特征值λ =0.656 5。将其对应的特征值加到不稳定解双峰解上可以观察到双峰解融合为一个孤立子,将特制值反向加到双峰解上会分裂为两个孤立子。因此在穿过与分裂的变化中,不稳定的双峰解充当了分水岭解的角色。在D点附近孤立子从REB 变迁到SPL,同样也是由一个不稳定的双峰解控制。C、D点附近分水岭解的区别在于:C点的分水岭解位于HIOP 的左侧,而D点的分水岭解位于HIOP 的右侧。

图4 C 点附近孤立子的时间演化图
从模拟的结果可以看到,在二维空间中分水岭解可以是不稳定的单峰解,也可以是不稳定的双峰解。与均匀空间中的分水岭解不同,非均匀空间中分水岭解在x方向是非对称的。分水岭解是控制孤立子碰撞后状态变迁的关键因素,因此,如果能够获得分水岭解的全局分歧图,根据分水岭解的不稳定特征,就可以知道在参数空间内将会发生哪些现象。利用Pseduo -Arclength 方法,从已知的单峰和双峰分水岭解出发可以得到的 全 局 分 歧 图(图5)。图5 中,实线代表双峰解(SP),虚线代表单峰解(SS)。从图5 中可以看出双峰解和单峰解并不是单独的分支,通过解的拓展可以相互连接起来。在相图中A-D点附近的4 种分水岭解都是相互关联的。还可以看到,除了4 种类型的分水岭解,还存在小的双峰解和单峰解,这些解也都是不稳定解。当孤立子与HIOP 正面碰撞以后其形状会向分水岭解接近,随着参数的变化,接近的轨道不同导致了各种现象的分化。在图5 中,虚线代表时均匀空间上的双峰解和单峰解,这也说明非均匀空间的分水岭解和均匀空间的分水岭解可以通过解的拓展连接起来。
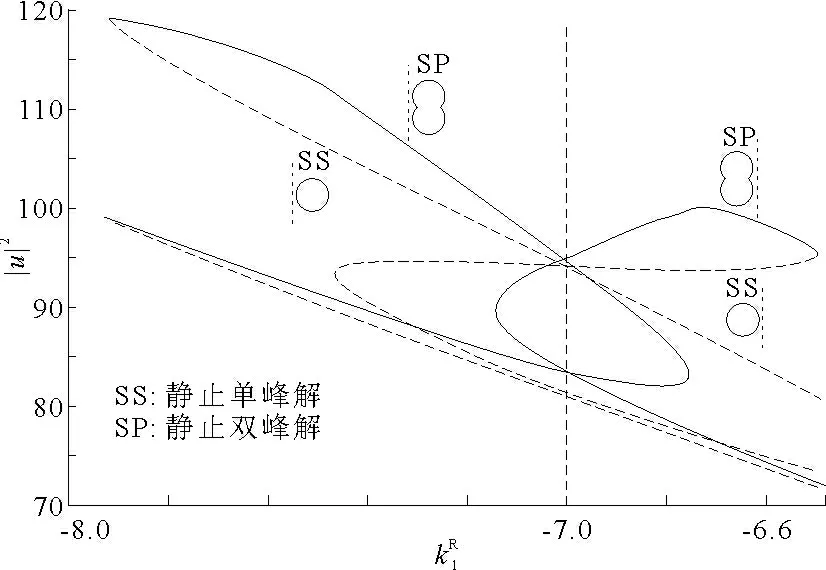
图5 kL1 = -7.0 的全局分歧图
3 结论
通过对Gas-Discharge 模型在二维非均匀空间上孤立子解的动力学分析,揭示了孤立子状态变迁的机理。在二维非均匀空间中,Gas - Discharge 模型的非均匀参数引起了多种形态的HIOP 解,其中4 种不稳定的HIOP 解充当了分水岭解的角色,这4 种解可以通过参数空间中的解拓展相互联系。HIOP 解的全局分歧图为解释孤立子的动力学特性提供了依据。
[1]PRUWINS S C,OR-GUIL M,BODE M,et al. Interacting pulses in three -component reaction -diffusion systems on two -dimensional domains[J]. Phys Rev Lett,1997(78):3781 -3784.
[2]NISHIURA Y,TERAMOTO T,UEDA K I. Dynamic transitions through scattors in dissipative systems[J].Chaos,2003,13(12):962 -972.
[3]YUAN X,TERAMOTO T,NISHIURA Y. Heterogeneity-induced defect bifurcation and pulse dynamics for a three - component reaction - diffusion system[J].Phys Rev E,2007,75(3):622 -630.
[4]NISHIURA Y,TERAMOTO T,YUAN X. Heterogeneity-induced spot dynamics for a three -component reaction - diffusion system[J]. Communications on Pure and Applied Analysis,2012(11):307 -338.
[5]NISHIURA Y,UEDA K I. A mathematical mechanism for instabilities in stripe formation on growing domains[J]. Physica D,2011(241):37 -59.
[6]NISHIURA Y,TERAMOTO T,UEDA K I. Scattering and separators in dissipative systems[J]. Phys Rev E,2003,71(5):621 -630.
[7]NISHIURA Y,TERAMOTO T,YUAN X,et al. Dynamics of traveling pulses in heterogeneous media[J].Chaos,2007,17(3):71 -75.
[8]NISHIURA Y,TERAMOTO T,UEDA K I. Scattering of traveling spots in dissipative systems[J]. Chaos,2005,15(4):75 -84.
[9]TERAMOTO T,SUZUKI K,NISHIURA Y. Rotational motion of traveling spots in dissipative systems[J].Phys Rev E,2009,77(4):620 -628.
[10]TERAMOTO T,YUAN X,BAR M,et al. Onset of unidirectional pulse propagation in an excitable medium with asymmetric heterogeneity[J]. Phys Rev E,2009,77(4):602 -607.

