ASYMPTOTIC BEHAVIOR OF GLOBAL SMOOTH SOLUTIONS FOR BIPOLAR COMPRESSIBLE NAVIER-STOKES-MAXWELL SYSTEM FROM PLASMAS∗
Yuehong FENG(冯跃红)
College of Applied Sciences,Beijing University of Technology,Beijing 100022,China Laboratoire de Math´ematiques,Universit´e Blaise Pascal,Clermont-Ferrand,63000,France
Shu WANG(王术)
College of Applied Sciences,Beijing University of Technology,Beijing 100022,China
Xin LI(李新)
Department of Mathematics and Computer Science,Xinyang Vocational and Technical College,
Xinyang 464000,China
ASYMPTOTIC BEHAVIOR OF GLOBAL SMOOTH SOLUTIONS FOR BIPOLAR COMPRESSIBLE NAVIER-STOKES-MAXWELL SYSTEM FROM PLASMAS∗
Yuehong FENG(冯跃红)
College of Applied Sciences,Beijing University of Technology,Beijing 100022,China Laboratoire de Math´ematiques,Universit´e Blaise Pascal,Clermont-Ferrand,63000,France
E-mail:fengyuehong001@163.com
Shu WANG(王术)
College of Applied Sciences,Beijing University of Technology,Beijing 100022,China
E-mail:wangshu@bjut.edu.cn
Xin LI(李新)
Department of Mathematics and Computer Science,Xinyang Vocational and Technical College,
Xinyang 464000,China
E-mail:lixin91600@163.com
This paper is concerned with the bipolar compressible Navier-Stokes-Maxwell system for plasmas.We investigated,by means of the techniques of symmetrizer and elaborate energy method,the Cauchy problem in R3.Under the assumption that the initial values are close to a equilibrium solutions,we prove that the smooth solutions of this problem converge to a steady state as the time goes to the infinity.It is shown that the difference of densities of two carriers converge to the equilibrium states with the norm‖·‖Hs-1,while the velocities and the electromagnetic fields converge to the equilibrium states with weaker norms than‖·‖Hs-1.This phenomenon on the charge transport shows the essential difference between the unipolar Navier-Stokes-Maxwell and the bipolar Navier-Stokes-Maxwell system.
bipolar compressible Navier-Stokes-Maxwell system;plasmas;global smooth solutions;energy estimates;large-time behavior
2010 MR Subject Classification 35L45;35L60;35Q60
1 Introduction
The Navier-Stokes-Maxwell system is used to simulate the transport of viscosity charged particles in plasmas[1,5,10,16,23].Usually,it takes the form of compressible Navier-Stokesequations forced by the electromagnetic fields,which is governed by the self-consistent Maxwell equations.In this paper,we consider the Cauchy problem for the bipolar compressible Navier-Stokes-Maxwell system:
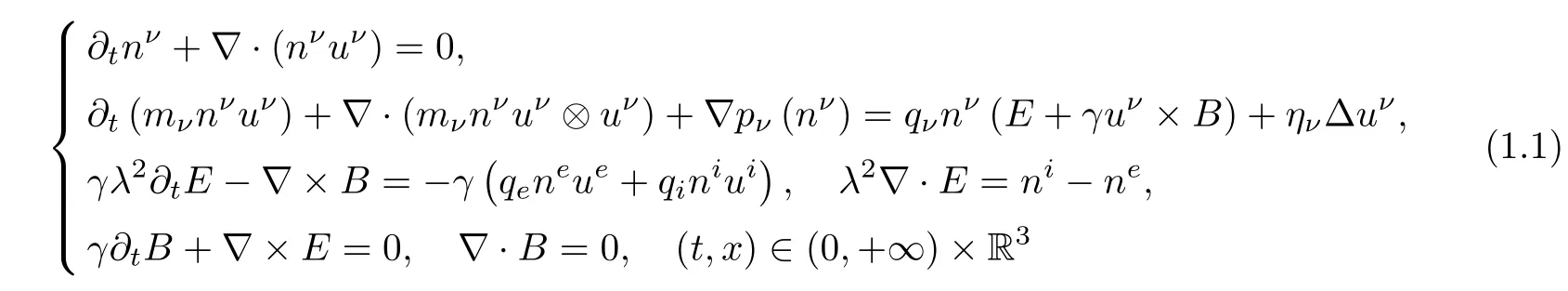
for ν=e,i.Here qe=-1(qi=1)is the charge of electrons(ions).The unknowns are the density nν>0,the velocity uν=(uν1,uν2,uν3),the pressure function pνwith p′ν(nν)>0 for ν=e,i,the electric field E=(E1,E2,E3)and the magnetic field B=(B1,B2,B3).Moreover,the constants mν> 0,ην>0,λ>0,1γ=c= (ε0µ0)-1/2,ε0andµ0are the mass,the viscosity coefficient,the scaled Debye length,the speed of light,the vacuum permittivity and permeability,respectively.Throughout this paper,we set mν=ην=λ=γ=1 without loss of generality.This is not an essential restriction in the investigation of global existence of smooth solutions for system(1.1).
For smooth solutions with nν>0,the second equation of(1.1)is equivalent to
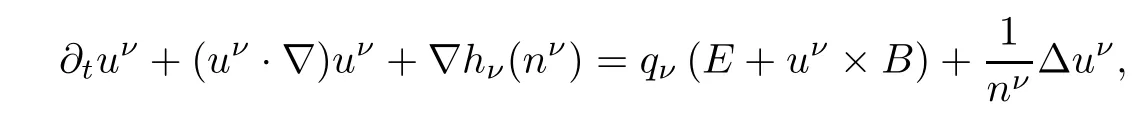
where hνis the enthalpy function defined by h′ν(nν)=1nνp′ν(nν).Since pνis strictly increasing on(0,∞),so is hν.
Then system(1.1)is equivalent to
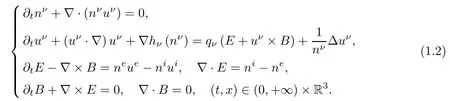
Initial conditions are given as
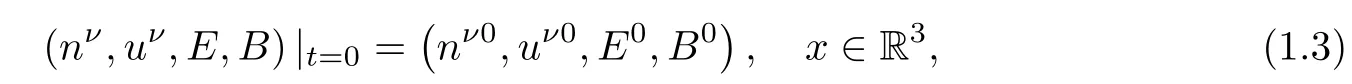
which satisfy the compatibility conditions:

The bipolar compressible Navier-Stokes-Maxwellsystem(1.2)is a symmetrizable hyperbolic parabolic system for nν>0.Then,according to the result of Kato[11]and the pioneering work of Matsumura-Nishida[14,15],the Cauchy problem(1.2)-(1.3)has a unique local smooth solution when the initial data are smooth.Here we are concerned with stabilities of global smooth solutions to(1.2)-(1.3)around a constant state being a particular solution of(1.2).It is easy to see that this constant state is necessarily given by
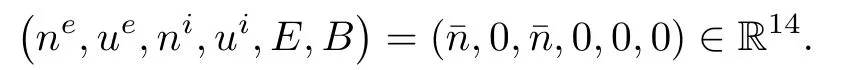
Proposition 1.1(Local existence of smooth solutions,see[11,13-15])Assume(1.4)holds.Let s≥4 be an integer and¯n≥const.>0.Suppose(nν0-¯n,uν0,E0,B0)∈Hs?R3?with nν0≥2κ for some given constant κ>0.Then there exists T>0 such that problem(1.2)-(1.3)has a unique smooth solution satisfying nν≥κ in[0,T]×R3and
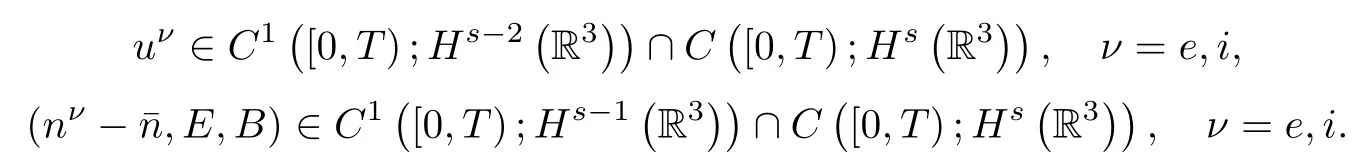
There are some mathematical investigations on the equations arising from plasmas.For one-dimensional isentropic Euler-Maxwell equations,Chen-Jerome-Wang[2]proved the global existence of weak solutions by using the compensated compactness method.For the threedimensional Euler-Maxwell equations,the existence of global smooth solutions with small amplitude to the periodic problem in the torus and to the Cauchy problem in R3is established by Ueda-Wang-Kawashima[26],Peng-Wang-Gu[22],Peng[18]and Xu[29],respectively.The decay rate of the smooth solution when time goes to infinity is discussed by Duan[4],Duan-Liu-Zhu[6],Feng-Wang-Kawashima[8],Wang-Feng-Li[27,28]and Ueda-Kawashima[25].For asymptotic limits with parameters,see[19-21,30]and references therein.For numerical analysis,see[3].In the case without damping,an additional relation B=∇×u was made in[9]to establish such a global existence result.Indeed,the variable B-∇×u is time invariant and the reduced linearized Euler-Maxwell system is of Klein-Gordon type,then its solution has a time decay of rate O(t-3/2).
For unipolar compressible Navier-Stokes-Maxwell system,by using the Green's function argument,Duan[5]proved the global existence and asymptotic behavior of smooth solutions around a steady state.For non-isentropic Navier-Stokes-Maxwell system,Feng-Peng-Wang[7]established the global existence and asymptotic behavior of smooth solutions,recently.To the authors'best knowledge,there are few analysis on the asymptotics and global existence for the bipolar Navier-Stokes-Maxwell system yet.The objective of this paper is to establish such a result.
The main results can be stated as follows.
Theorem 1.2(Global existence of smooth solutions) Let s≥4 be an integer.Assume(1.4)holds and¯n≥const.>0.Then there exist constants δ0>0 small enough,independent of any given time t>0,such that if

the Cauchy problem(1.2)-(1.3)has a unique global solution
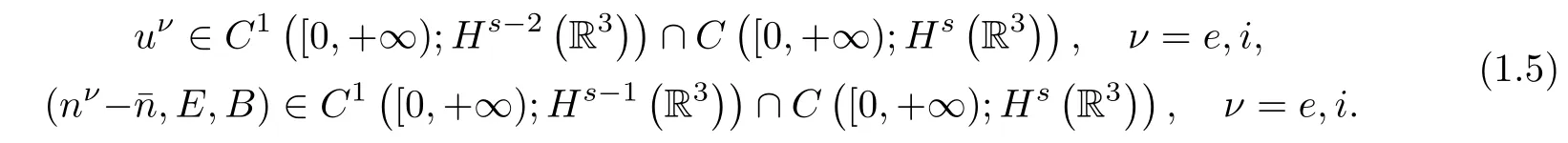
Theorem 1.3(Large-time behavior of smooth solutions)Under the assumptions of Theorem 1.2,the global smooth solution satisfies
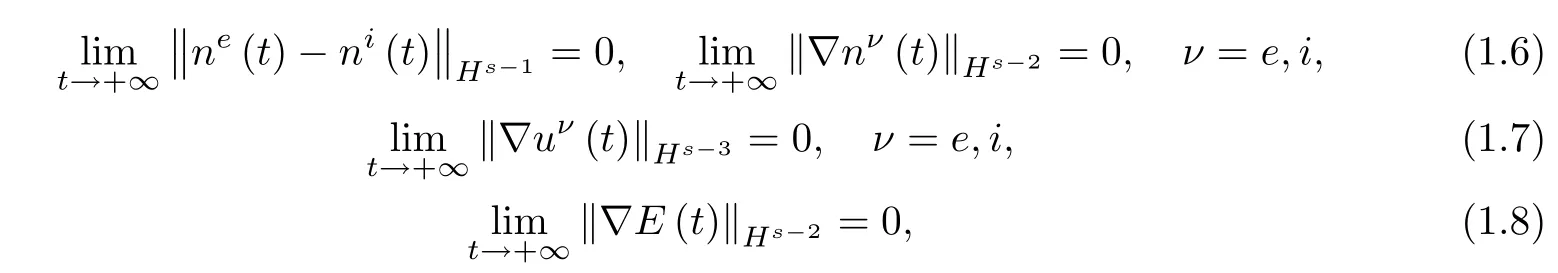
and
Remark 1.4 It should be emphasized that the velocity viscosity term of the bipolar Navier-Stokes-Maxwell system(1.2)plays a key role in the proof of Theorem 1.2.
Remark 1.5 Similarly,we may establish estimates(1.8)and(1.9)for the smooth solutions of the unipolar Navier-Stokes-Maxwell system.This implies the large-time behavior of the electromagnetic field in that case.
The proof of Theorem 1.2 and Theorem 1.3 based on techniques of symmetrizer and elaborate weighted energy method.It should be pointed out that the bipolar compressible Navier-Stokes-Maxwell system is much more complex than the unipolar compressible Navier-Stokes-Maxwell system.For example,Duan[5]introduced a new variable and reduced directly the unipolar Navier-Stokes-Maxwell system to a symmetric system by using a scaling technique. However,this technique doesn't work for the bipolar Navier-Stokes-Maxwell system due to the complexity of the coupled ions equations.To overcome this difficulty,we choose a new symmetrizer.Now,let us explain the main difference of proofs in the unipolar and bipolar Navier-Stokes-Maxwell systems.From(1.2),it is easy to see that∇uνis dissipative.By using the weighted energy method,we obtain an energy estimate for∇uνin L2?[0,T];Hs?R3??(see Lemma(2.4)).The key step for proving the global existence with asymptotic properties of solutions is to control nν-¯n in L2?[0,T];Hs?R3??.In the unipolar Navier-Stokes-Maxwell system[5],this is achieved in estimate
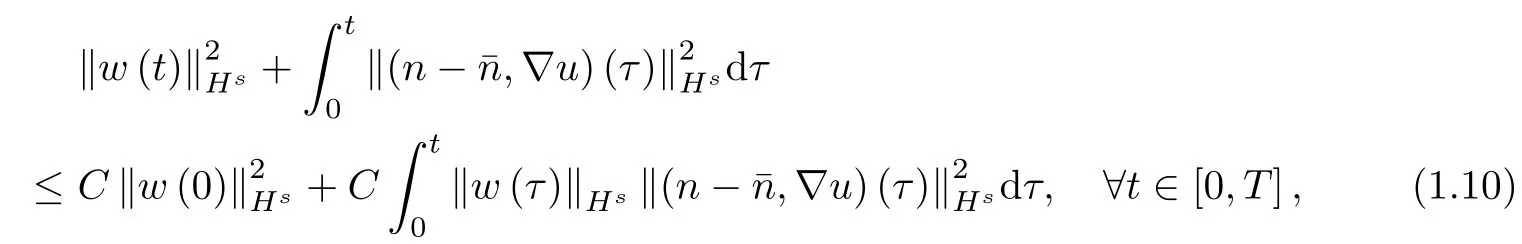
The rest of this paper is arranged as follows.In Section 2,we deal with the global existence for smooth solutions.The main goal is to prove Theorem 1.2 by establishing energy estimates. In Section 3,we complete the proof of Theorem 1.3 by establishing dissipations estimates for electromagnetic field,and the large-time behavior of the solutions is presented.
2 Global Existence
It is well known that the global existence of smooth solutions follows from the local existence and uniform estimates of solutions with respect to t.The main task of this section is devoted to the uniform estimates for proving Theorems 1.2.
2.1 Preliminary
We first introduce some notations for later use.The expression f~g means γg≤f≤1γg for a constant 0<γ<1.We denote by‖·‖sthe norm of the usual Sobolev space Hs(R3),andby‖·‖and‖·‖∞the norms of L2(R3)and L∞(R3),respectively.We also denote by<·,·>the inner product over L2(R3).For a multi-index α=(α1,α2,α3)∈N3,we denote
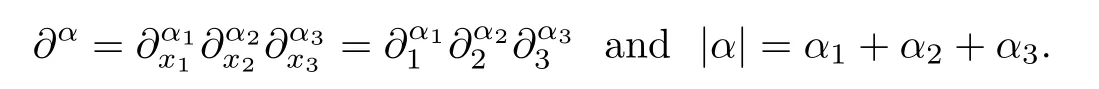
For α=(α1,α2,α3)and β=(β1,β2,β3)∈N3,β≤α stands for βj≤αjfor j=1,2,3,and β<α stands for β≤α and β/=α.
The Leibniz formulas
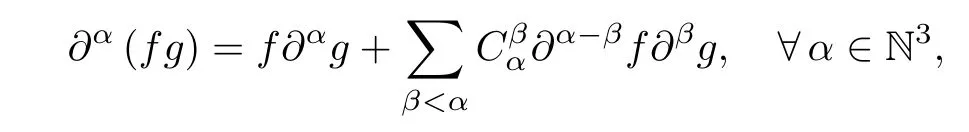
where Cβα>0 for β<α are constants.
The following Lemmas will be needed in the proof of Theorem 1.2.
Lemma 2.1(Moser-type calculus inequalities,see[12,13]) Let s≥1 be an integer. Suppose u∈Hs(R3),∇u∈L∞(R3)and v∈Hs-1(R3)∩L∞(R3).Then for all multi-index α with 1≤|α|≤s,one has∂α(uv)-u∂αv∈L2(R3)and
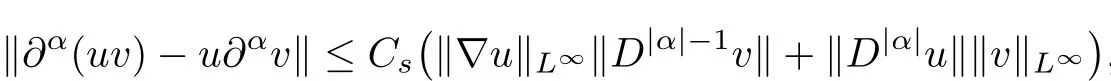
where
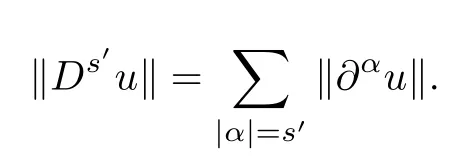
Furthermore,if s≥3,then the embedding Hs-1(R3)→L∞(R3)is continuous and we have
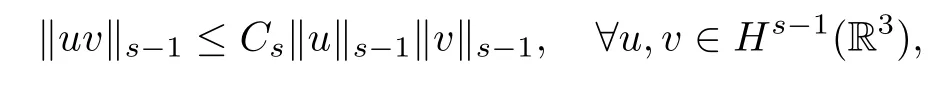
and for all smooth function f and u,v∈Hs(R3),
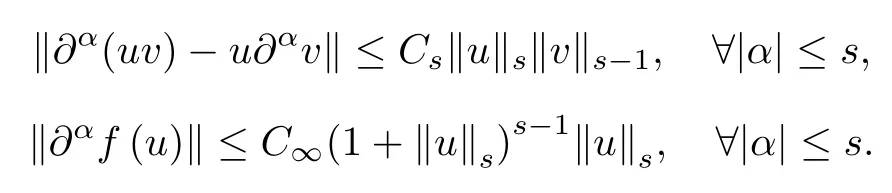
Lemma 2.2(see[7])For∇u∈H1,there exists a constant C>0 such that
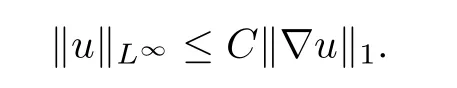
Suppose(nν,uν,E,B)is a smooth solution of Cauchy problem for the bipolar Navier-Stokes-Maxwell system(1.2)with initial conditions(1.3)which satisfies(1.4).
Set

and
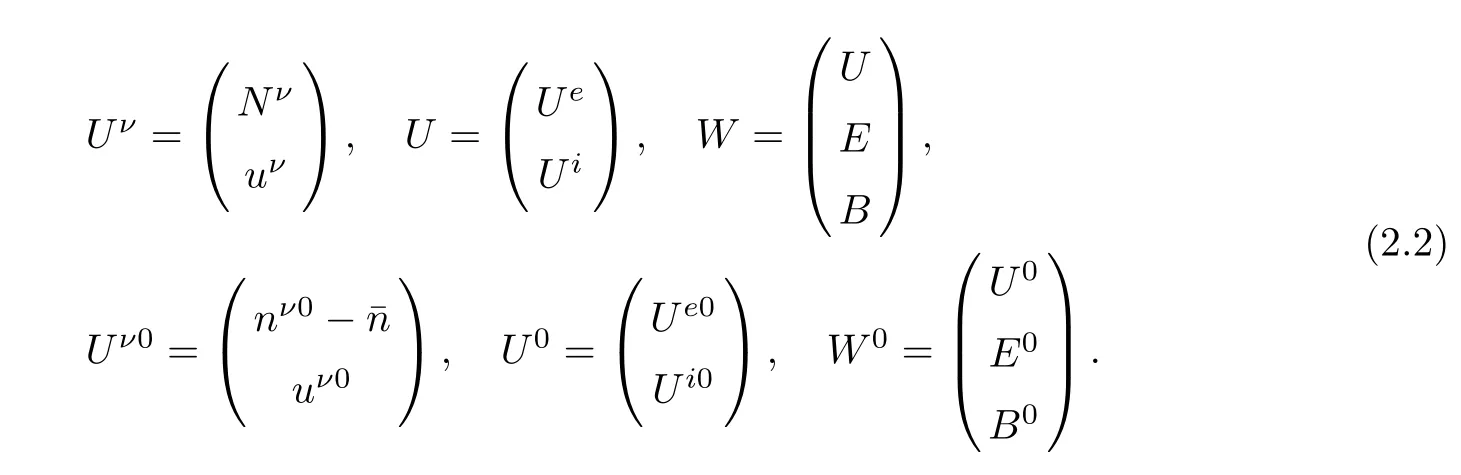
Using(2.1),system(1.2)can be written as
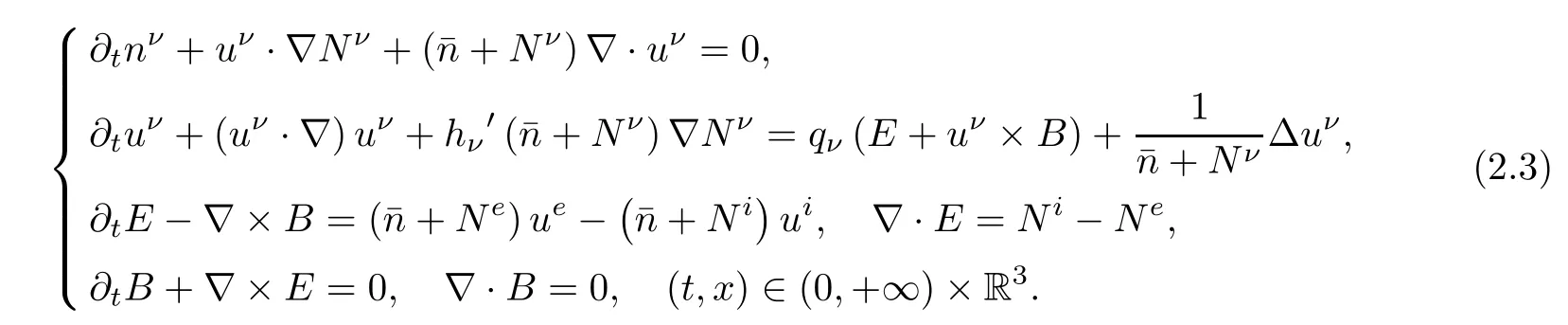
Furthermore,using(2.2),the Navier-Stokes equations of(2.3)can be rewritten as
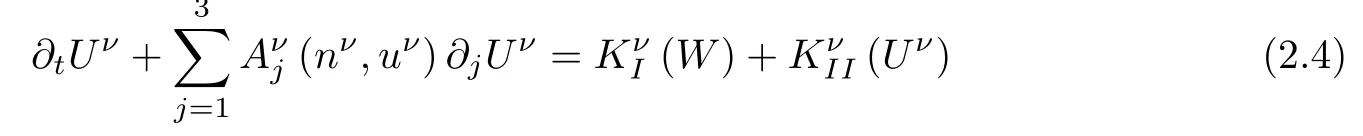
with
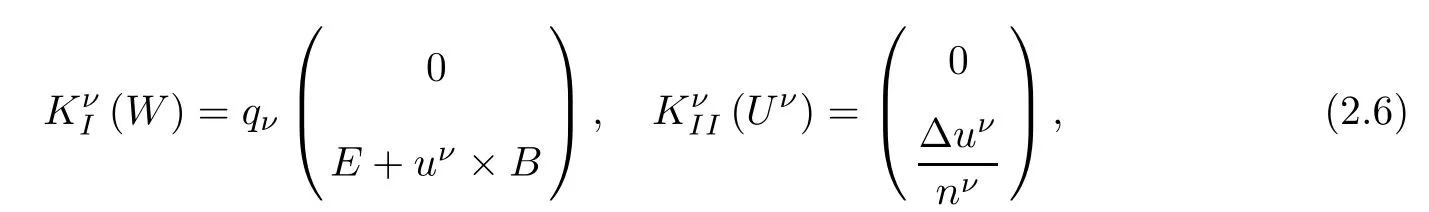
where(e1,e2,e3)is the canonical basis of R3,I3is the 3×3 unit matrix,Vjdenotes the jth component of V∈R3.
It is clear that(2.4)for Uνis symmetrizable hyperbolic parabolic when nν=¯n+Nν>0. More precisely,since¯n≥const.>0 and we consider small solutions for which Nνis close to zero,we have nν=¯n+Nν≥const.>0.Let
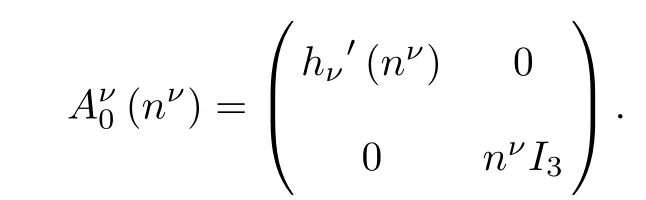
Then
1.5 就业市场管理体制有待完善。随着我国改革开放的进一步深化发展,高校毕业生制度经历了一个由“统一分配”到“双向选择、自主择业”的转变过程。在此背景下,高校毕业生就业市场仍处于不断发展完善中,其管理体制和相关保障机制不健全,无法有效维护毕业生的正当就业权益,不利于其稳定就业和高效就业。
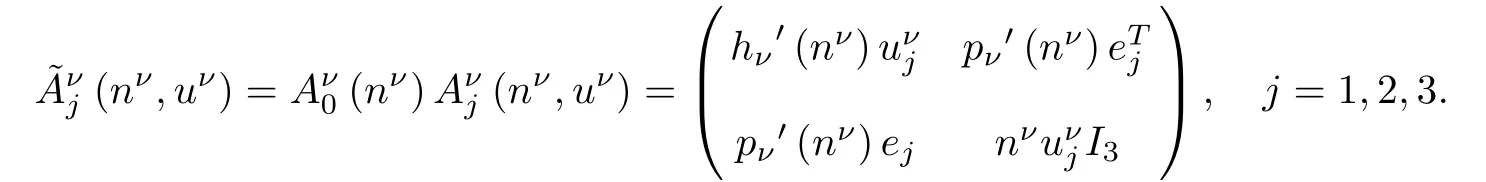
Since Aν0is symmetric positively definite and˜Aνjis symmetric for all 1≤j≤3,system(2.4)is symmetrizable hyperbolic parabolic.
Let T>0 and W be a smooth solution of(2.3)defined on time interval[0,T]with initial data W0.This local solution is given by Proposition 1.1.From now on,we define

and by C >0 various constants independent of any time t and T.From the continuous embedding Hs(R3)→L∞?R3?for s≥2,there exists a constant Cm>0 such that
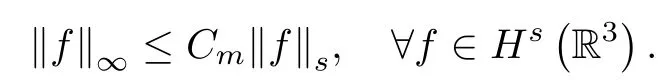
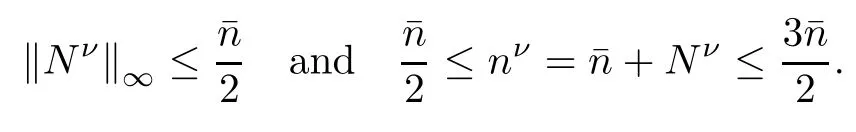
Moreover,by Lemma 2.1,for any smooth function g one has
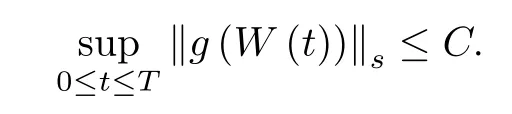
Note that in the proof of Lemmas 2.3-2.5,we only suppose
2.2 Energy Estimates
In this subsection,we establish the classical energy estimate for W.The first lemma concerns the zero order energy estimate.
Lemma 2.3 Under the assumptions of Theorem 1.2,if ωT≤¯n

Proof Taking the inner product of(2.4)with 2Aν0(nν)Uνin L2?R3?yields the classical energy equality for Uν:
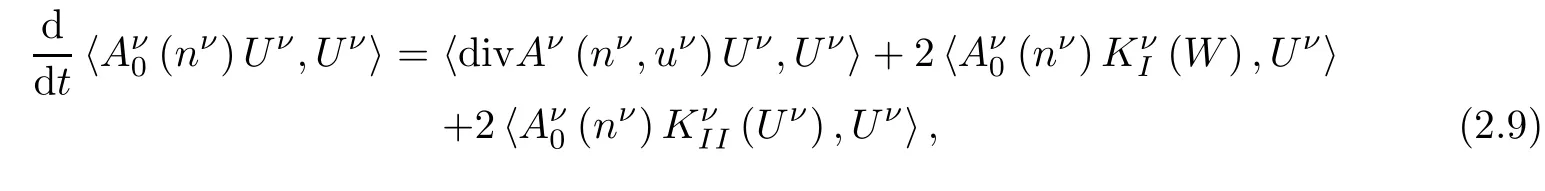
where
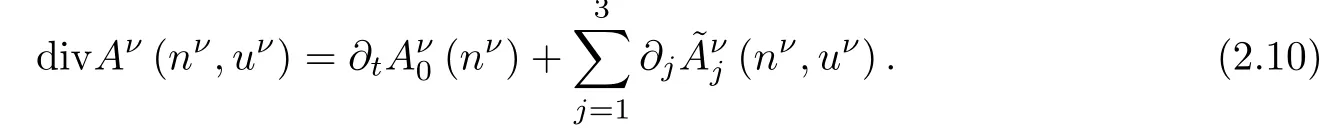
Since
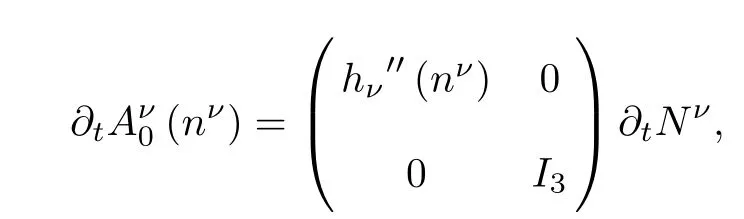
using the first equation of(2.3),Lemma 2.2 and ωT≤¯n2Cm,we have
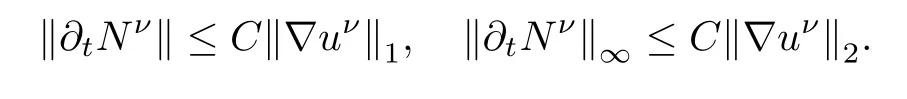
Then,
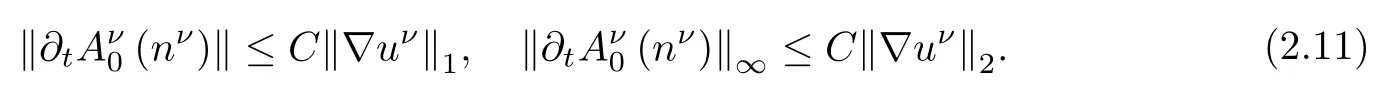
Now,let us estimate each term on the right hand side of(2.9).For the first term,using(2.5),(2.10),(2.11)and Lemma 2.2,we get
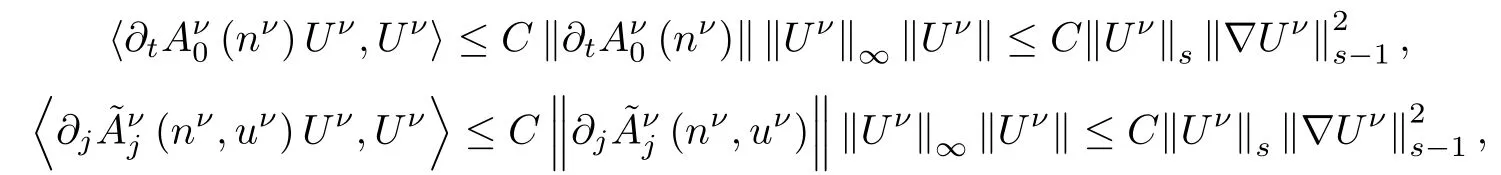
and then
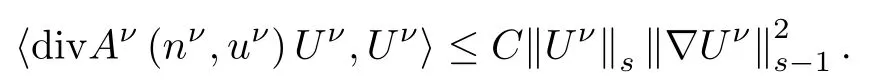
For the last two terms,using(2.6),the fact that uν·(uν×B)=0 and an integration by parts,we have
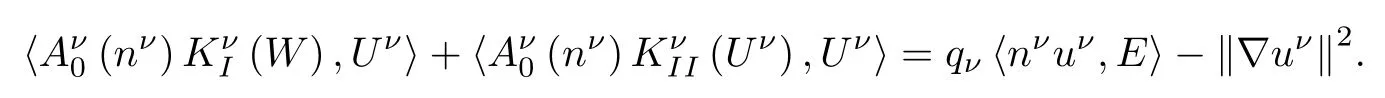
Therefore,
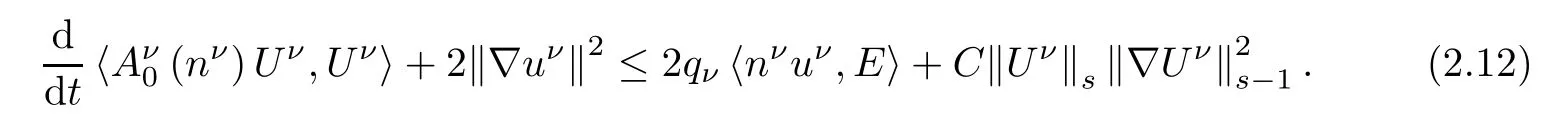
On the other hand,a standard energy estimate for the Maxwell equations of(2.3)yields
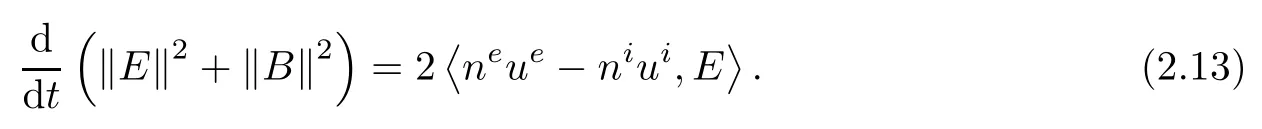
Hence,the cancellation of the termneue-niui,Ein(2.12)and(2.13)exists.The sum of(2.12)and(2.13)for ν=e,i,we obtain
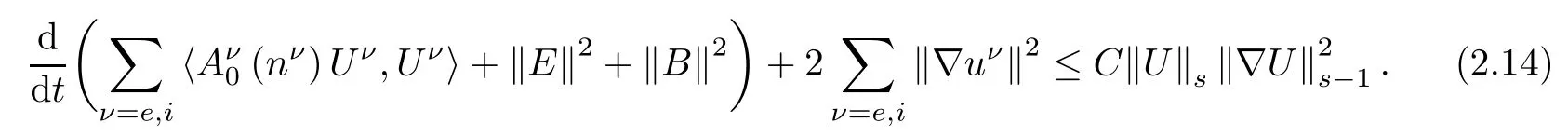
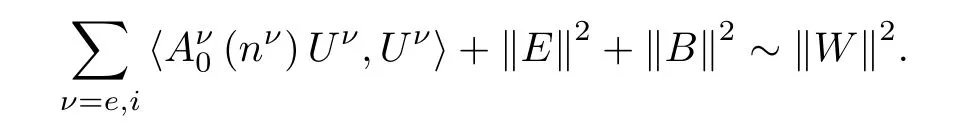
Therefore,(2.8)follows from integrating(2.14)over(0,t)with t∈[0,T].This completes the proof of Lemma 2.3. □
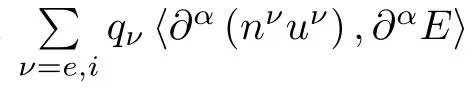
For Navier-Stokes equations in(2.3),we define the dissipation function Ds(t)by
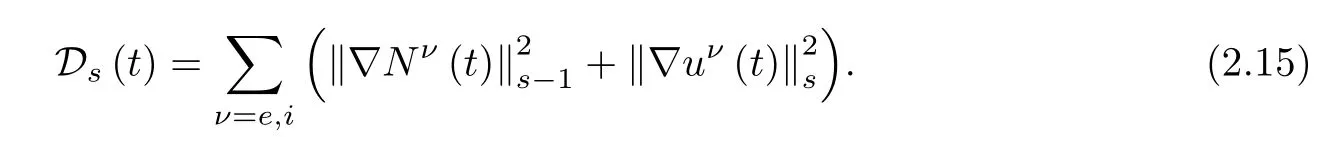
Lemma 2.4 Under the assumptions of Theorem 1.2,if ωT≤¯n2Cm,it holds
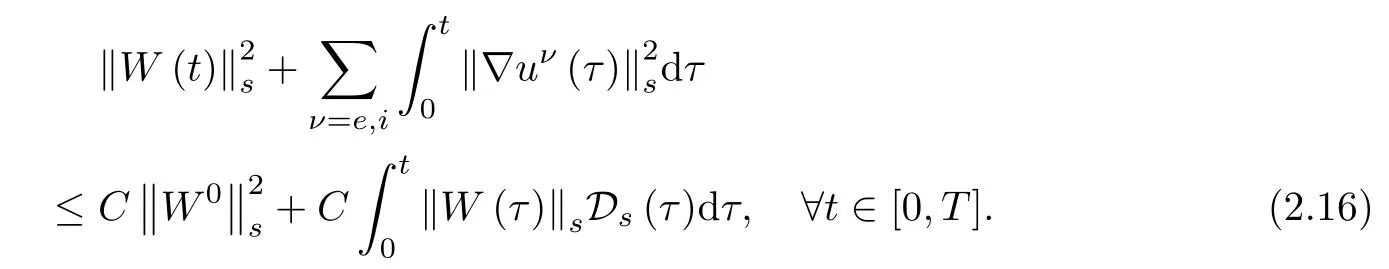
Proof For α∈N3with 1≤|α|≤s.Applying∂αto(2.4)and multiplying the resulting equations by the symmetrizer matrix Aν0(nν),we have

where
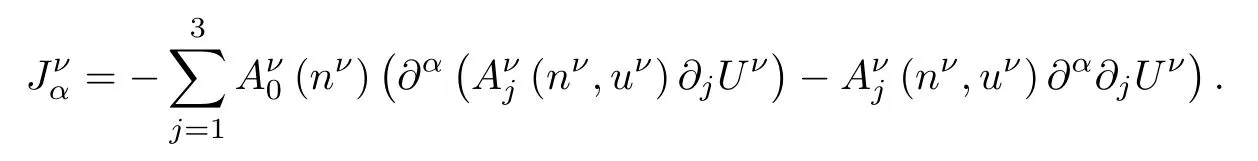

Taking the inner product of(2.17)with 2∂αUνin L2(R3),we obtain
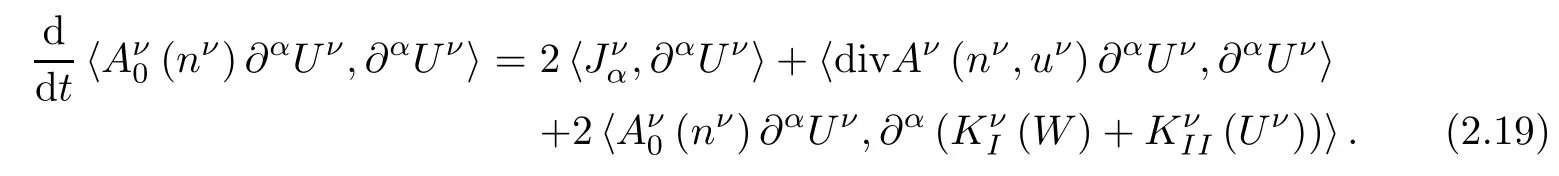
Using(2.10),(2.11)and the definition of,we have

Now,let us estimate each term on the right hand side of(2.19).For the first two terms,it follows from(2.18),(2.20)and Cauchy-Schwarz inequality that
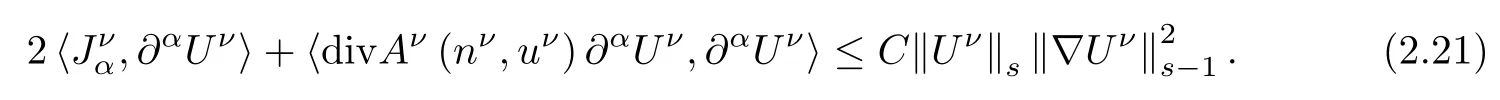
For the last term,using(2.6),Leibniz formulas,Lemma 2.1 and Lemma 2.2,it holds
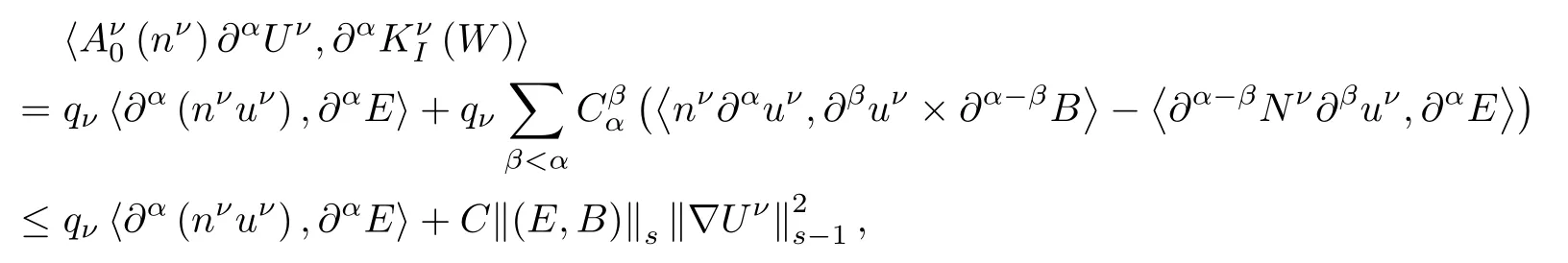
and
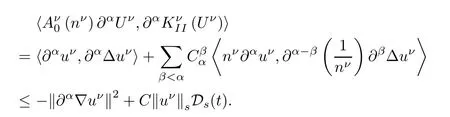
Then,
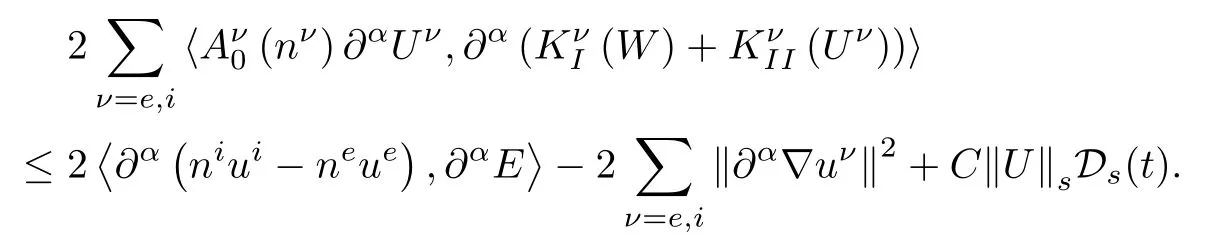
This inequality together with(2.19)and(2.21)yields
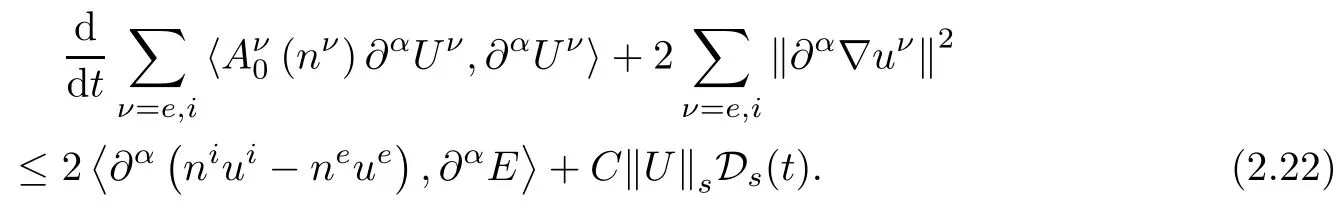
On the other hand,an easy high order energy estimate for the Maxwell equations of(2.3)gives
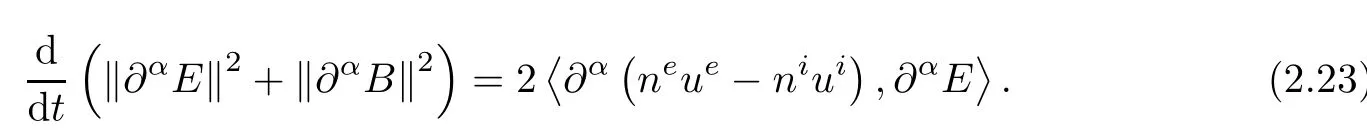
Due to the choice of symmetrizer)we see that the cancellation of the term
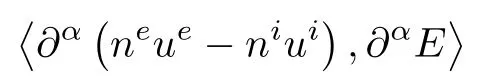
in(2.22)and(2.23)exists.It follows from(2.22)and(2.23)that
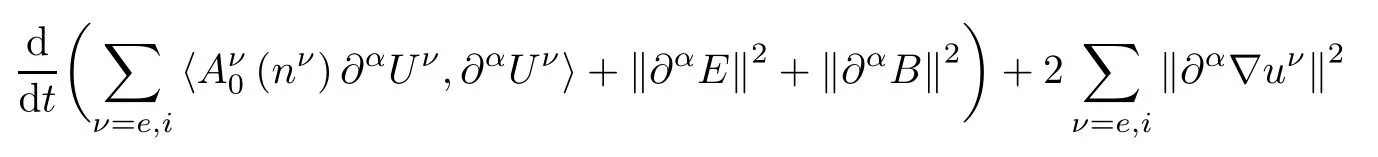

Noting the fact that
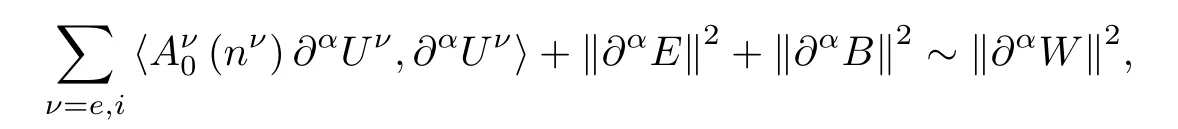
summing(2.24)for all α with 1≤|α|≤s,and then integrating over[0,t],together with(2.8),we get(2.16).This completes the proof of Lemma 2.4. □
Estimate(2.16)stands for the dissipation of∇uν.It is clear that this estimate is not sufficient to control the high order term on the right hand side of(2.16)and the dissipation estimates of Nνis necessary.
Lemma 2.5 Under the assumptions of Theorem 1.2,if ωT≤¯n
2Cm,there exist positive constants C1and C2,independent of t and T,such that
Proof For α∈N3with|α|≤s-1,applying∂αto the second equation of(2.3),and then taking the inner product of the resulting equation with∇∂αNνin L2?R3?,we have
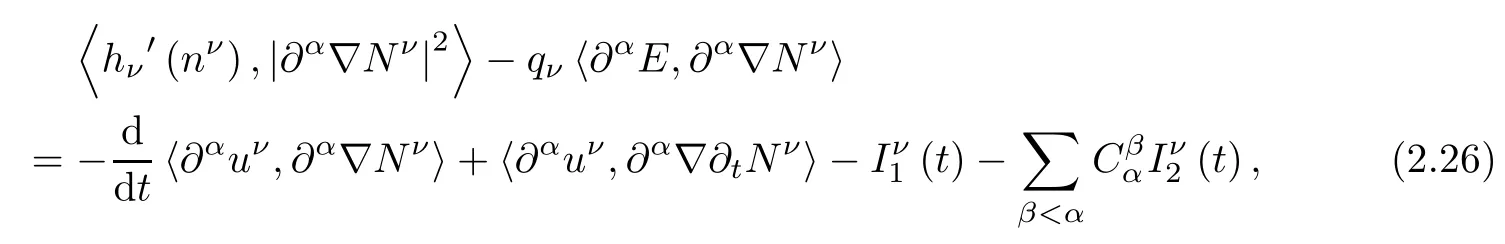
where
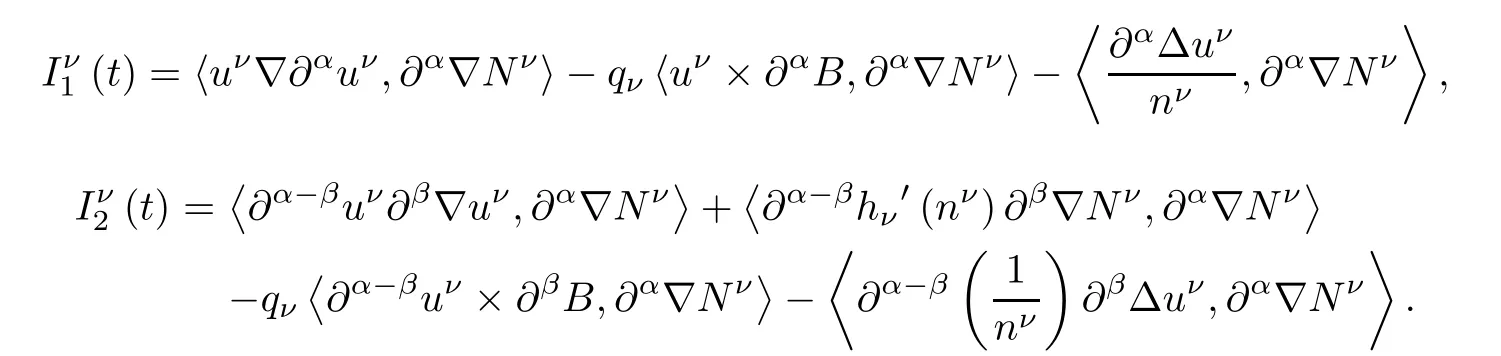
Now,let us estimate each term in(2.26).First,noting thatand hνis a strictly increasing function on(0,+∞),we haveHence,
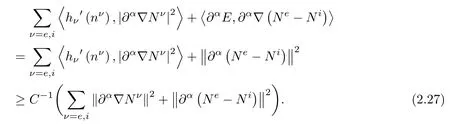
Next,using the first equation of(2.3)and an integration by parts,we get
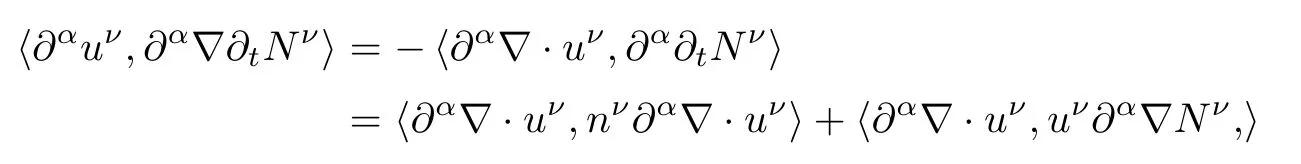
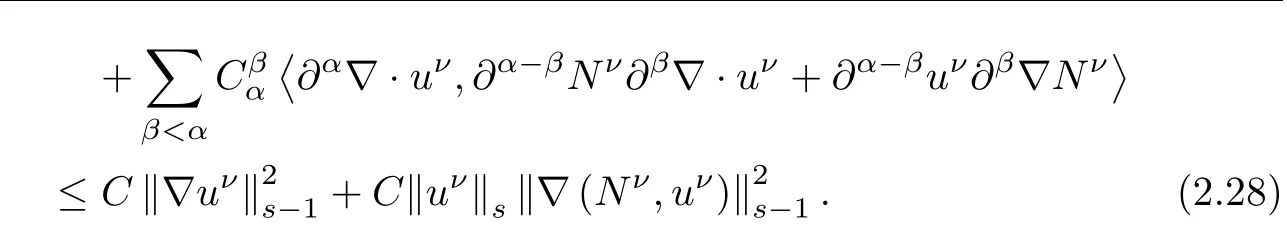
When|α|=0,from Lemma 2.2 and Cauchy-Schwarz inequality,we have
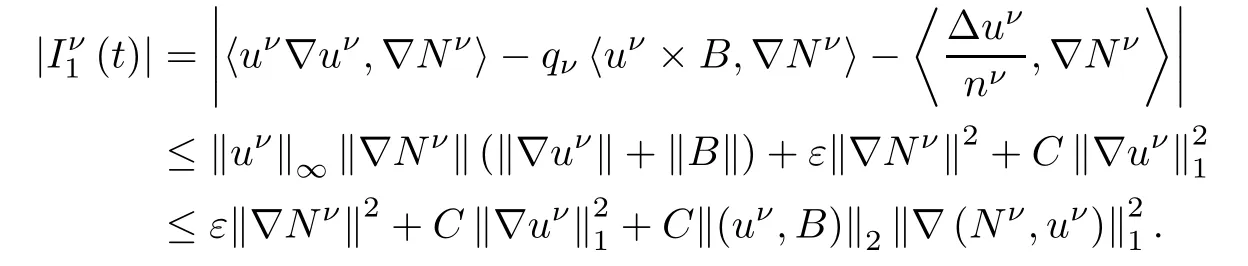
And when|α|≥1,it follows similarly that
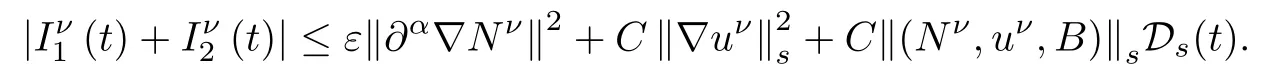
These last two inequalities together with(2.26)-(2.28)yields
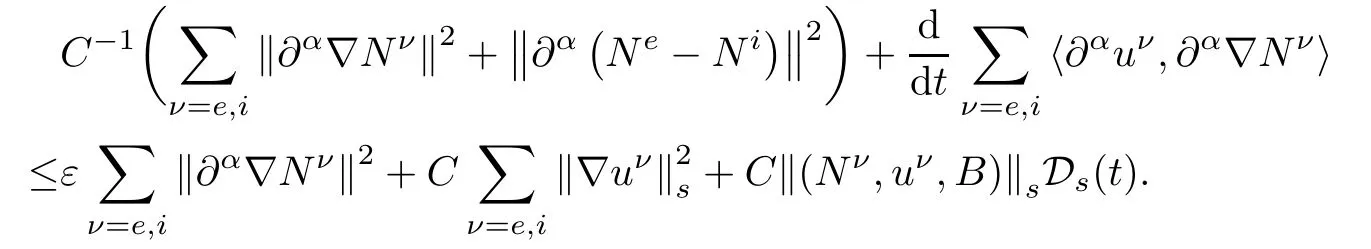
Summing up this inequality for all|α|≤s-1 and choosing ε>0 small enough,so that the term ε||∂αNν||2can be controlled by that in the left hand side.Hence,integrating the resulting equation over[0,t],we have
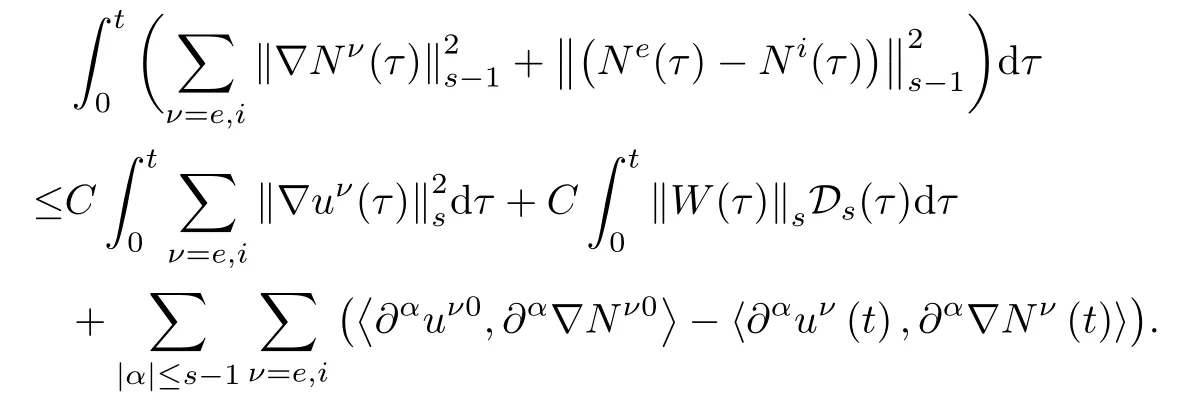
Finally,
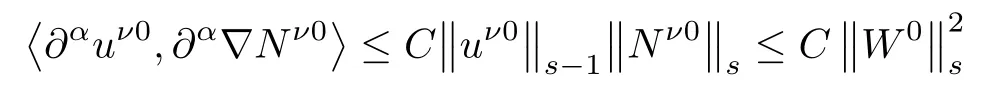
and
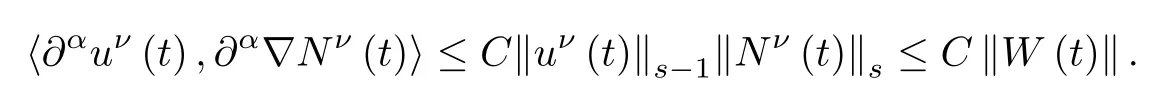
Therefore,together with(2.16),we obtain(2.25).This completes the proof of Lemma 2.5.□
Proof of Theorem 1.2 By Lemma 2.5,we find that if C2ωT<1,the integral term on the right hand side of(2.25)may be controlled by that of the left hand side.It follows that
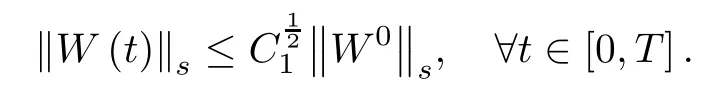
Then,it suffices to choose a constant δ0small enough such that
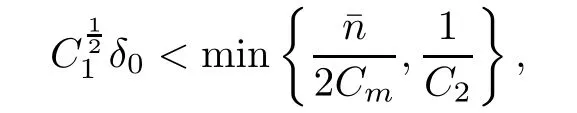
3 Large Time Behavior
3.1 Dissipation of the Electromagnetic Fields
The large time behavior of smooth solutions follows from uniform energy estimates of Nν,∇uν,∇E and∇2G with respect to T in L2([0,T];Hs′(R3))
for appropriate integers s′≥1.We establish these estimates in the following two lemmas.
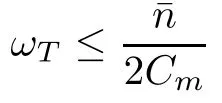
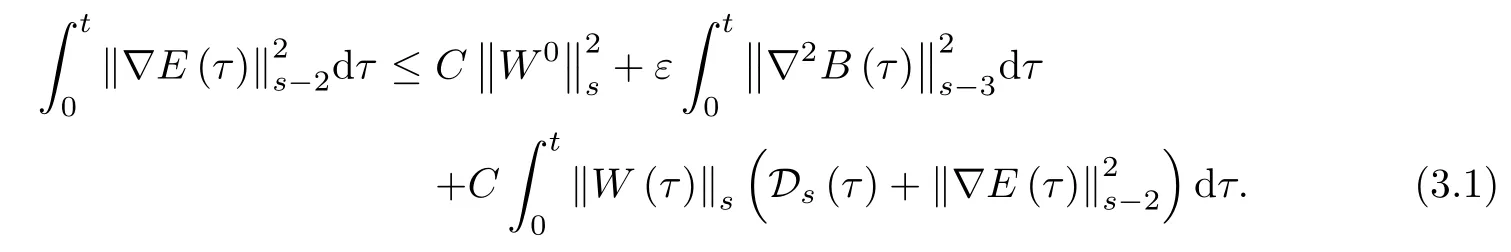
Proof For α∈N3with 1≤|α|≤s-1,applying∂αto the second equation of(2.3)and taking the inner product of the resulting equations with∂αE in L2(R3),we have

where
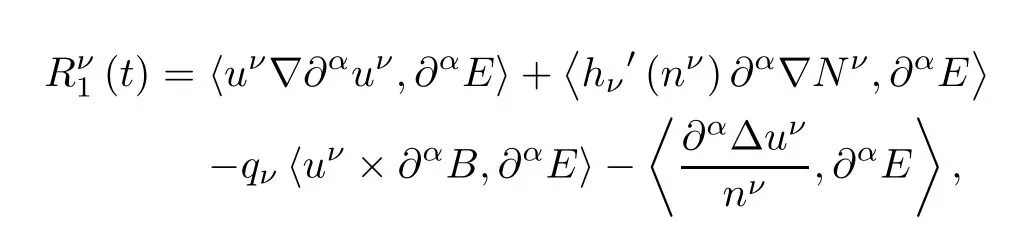
and
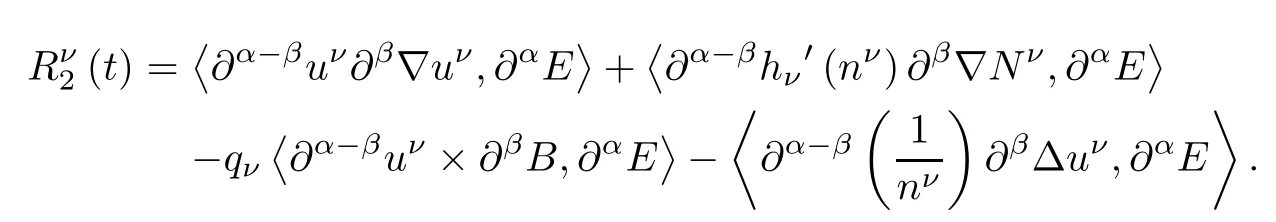
Using the electric field equation in(2.3),Cauchy-Schwarz inequality and an integration by parts,we obtain
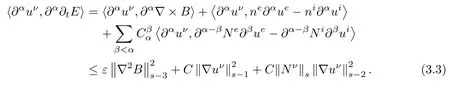
Similarly as before,we obtain
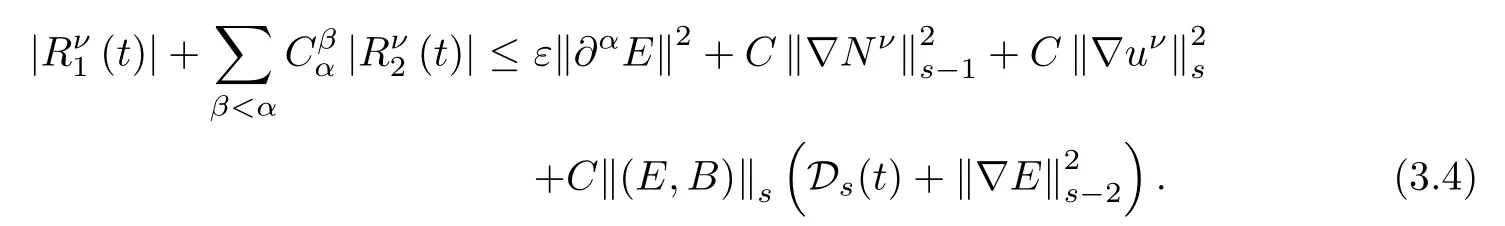
It follows from(3.2)-(3.4)that
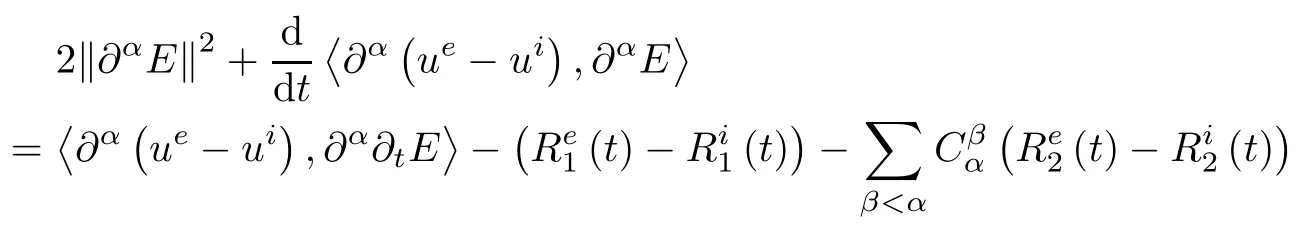
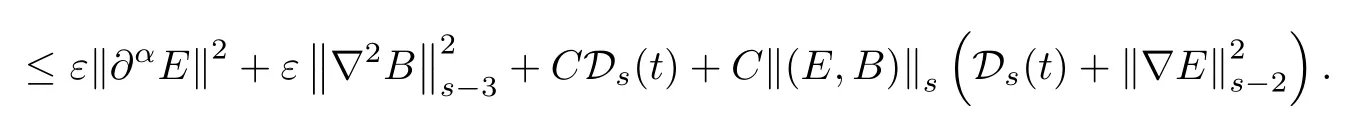
Summing up this inequality for all α with 1≤|α|≤s-1 and taking ε>0 so small that the term ε‖∂αE‖2can be controlled by that in the left hand side,and then integrating the resulting equation over[0,t],using(2.25)and noting the fact that for all t∈[0,T],
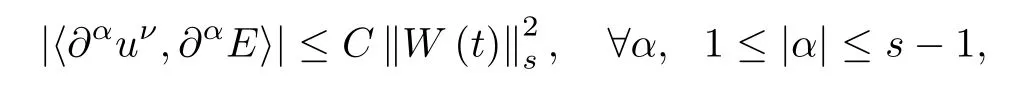
we obtain(3.1).This completes the proof of Lemma 3.1. □
Lemma 3.2 Under the assumptions of Theorem 1.2,if if ωT≤¯n
2Cmfor all t∈[0,T],it holds
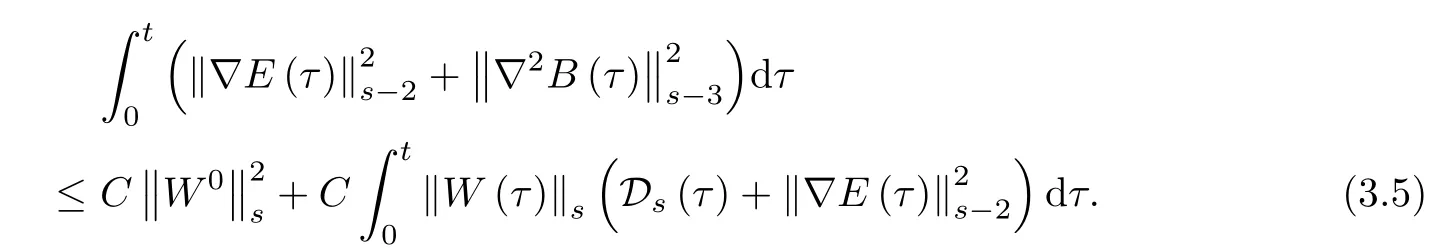
Proof For α∈N3with 1≤|α|≤s-2,applying∂αto the electric field equation in(2.3)and taking the inner product of the resulting equation with-∇×∂αB,we obtain
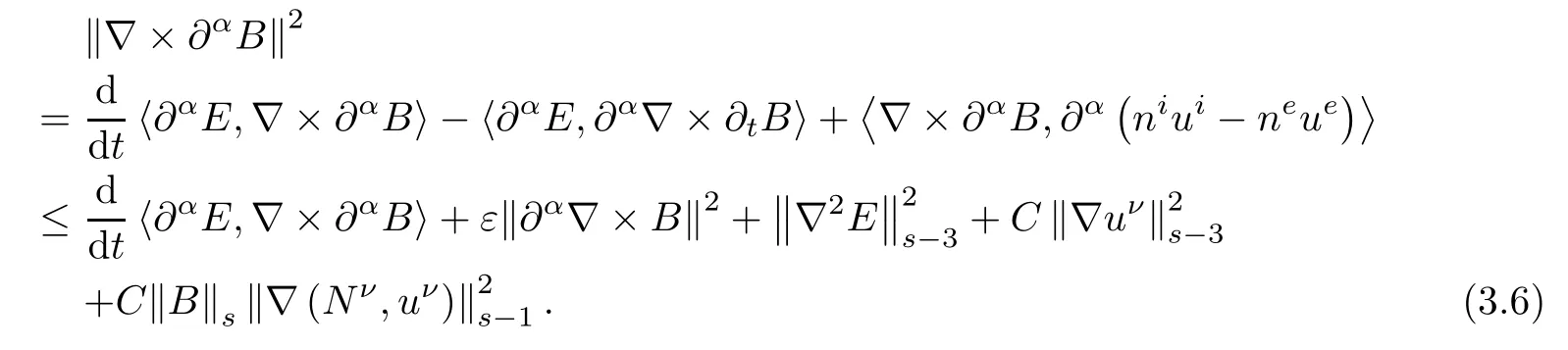
Note that for all t∈[0,T],
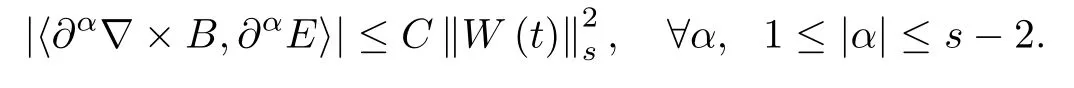
Let ε>0 be small enough,integrating(3.6)over[0,T]and summing for all 1≤|α|≤s-2,together with(3.1),we get(3.5).In this estimate we have used
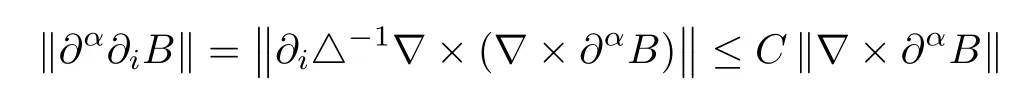
for 1≤i≤3,due to the fact that∇·B=0 and∂i△-1∇is bounded from Lpto itself with 1<p<∞,see[24].This completes the proof of Lemma 3.2. □3.2 Proof of Theorem 1.3
Recall the following Lemma that is used in the following.
Lemma 3.3 Let f:(0,+∞)→ R be a uniformly continuous function such that f∈ThenIn particular,the conclusion holds when f∈L1(0,+∞)∩W1,+∞(0,∞).
Now let us establish the large time behavior of solutions and complete the proof of Theorem 1.3.From Lemma 2.5,there exists a constant δ0such that if ωT≤δ0,it holds
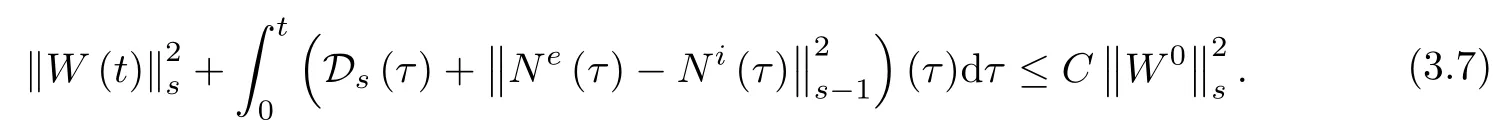
Since ne-ni=Ne-Niand∇nν=∇Nν,this together with(2.15)implies that
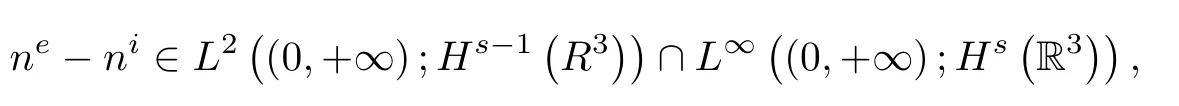
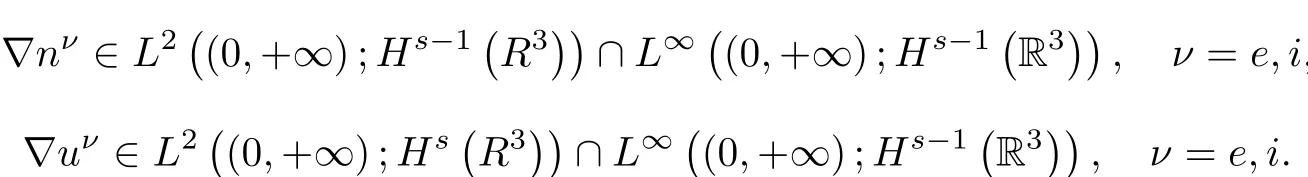
Using the Navier-Stokes equations in(2.3),we obtain
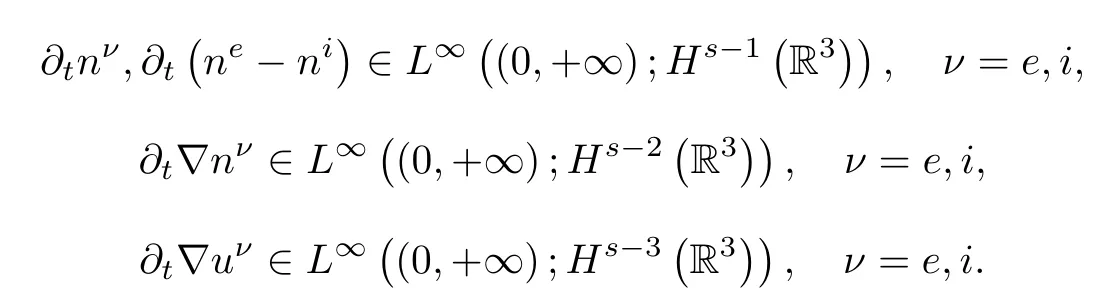
Then
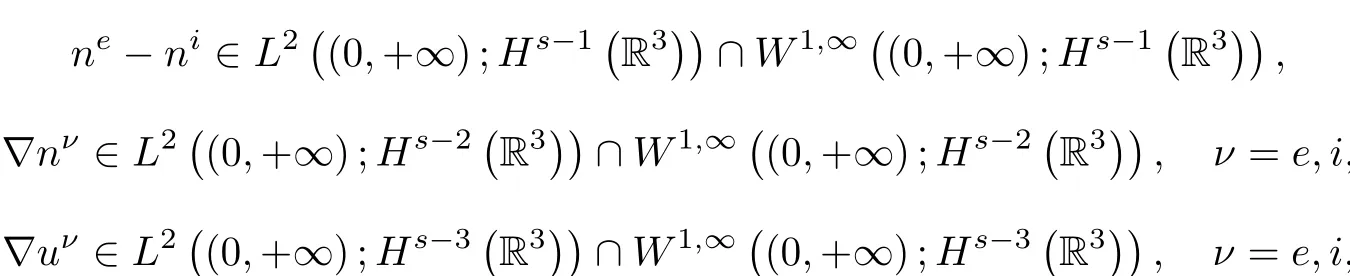
which imply(1.6)-(1.7).
Similarly as before,from(3.5)and(3.7),we get
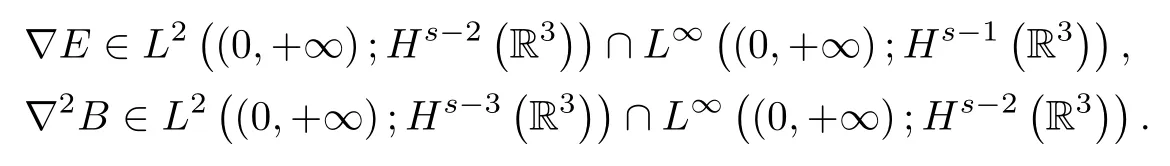
It follows from the Maxwell equations in(2.3)that
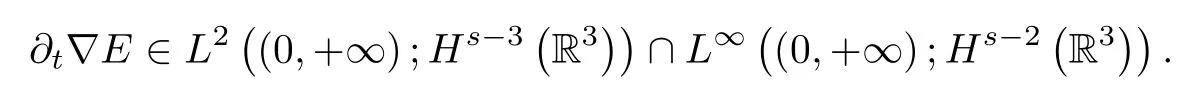
Therefore,
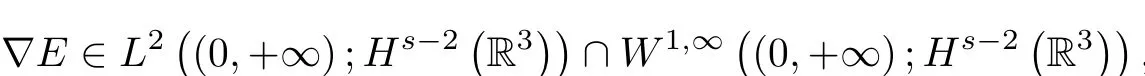
which implies(1.8).We further deduce that
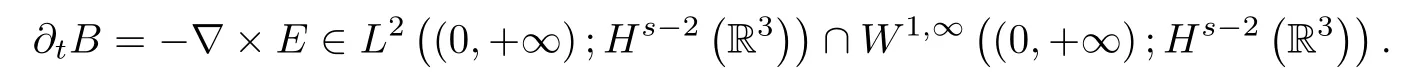
Then
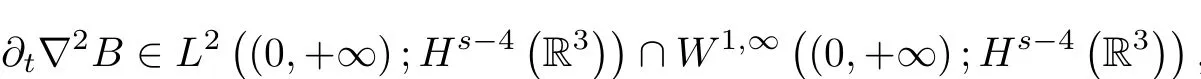
which implies(1.9).This completes the proof of Theorem 1.3. □
[1]Chen F.Introduction to Plasma Physics and Controlled Fusion,Vol 1.New York:Plenum Press,1984
[2]Chen G Q,Jerome J W,Wang D H.Compressible Euler-Maxwell equations.Transport Theory and Statistical Physics,2000,29:311-331
[3]Degond P,Deluzet F,Savelief D.Numerical approximation of the Euler-Maxwell model in the quasineutral limit.J Comput Phys,2012 231:1917-1946
[4]Duan R J.Global smooth flows for the compressible Euler-Maxwell system:relaxation case.J Hyperbolic Differential Equations,2011 8:375-413
[5]Duan R J.Green's function and large time behavior of the Navier-Stokes-Maxwell system.Anal Appl,2012,10:133-197
[6]Duan R J,Liu Q Q,Zhu C J.The Cauchy problem on the compressible two-fluids Euler-Maxwell equations. SIAM J Math Anal,2012,44:102-133
[7]Feng Y H,Peng Y J,Wang S.Asymptotic behavior of global smooth solutions for full compressible Navier-Stokes-Maxwell equations.Nonlinear Anal Real,2014,19:105-116
[8]Feng Y H,Wang S,Kawashima S.Global existence and asymptotic decay of solutions to the non-isentropic Euler-Maxwell system.Math Mod Meth Appl Sci,2014,24:2851-2884
[9]Germain P,Masmoudi N.Global existence for the Euler-Maxwell system.Ann Sci Ecole Norm S,2014,47(3):469-503
[10]J¨ungel A.Quasi-Hydrodynamic Semiconductor Equations.Birkh¨auser,2001
[11]Kato T.The Cauchy problem for quasi-linear symmetric hyperbolic systems.Arch Ration Mech Anal,1975,58:181-205
[12]Klainerman S,Majda A.Singular limits of quasilinear hyperbolic systems with large parameters and the incompressible limit of compressible fluids.Comm Pure Appl Math,1981 34:481-524
[13]Majda A.Compressible Fluid Flow and Systems of Conservation Laws in Several Space Variables.New York:Springer-Verlag,1984
[14]Matsumura A,Nishida T.The initial value problem for the equation of motion of compressible viscous and heat-conductive fluids.Proc Japan Acad,Ser A,1979,55:337-342
[15]Matsumura A,Nishida T.The initial value problem for the equation of motion of viscous and heatconductive gases.J Math Kyoto Univ,1980,20:67-104
[16]Markowich P,Ringhofer C A,Schmeiser C.Semiconductor Equations.Springer,1990
[17]NishidaT.Nonlinearhyperbolicequationsand related topicsin fluidsdynamics.Publications Math´ematiques d'Orsay,Universit´e Paris-Sud,Orsay,1978:78-02
[18]Peng Y J.Global existence and long-time behavior of smooth solutions of two-fluid Euler-Maxwell equations. Ann I H Poincare-AN,2012,29:737-759
[19]Peng Y J,Wang S.Convergence of compressible Euler-Maxwell equations to incompressible Euler equations. Comm Part Diff Equations,2008,33:349-376
[20]Peng Y J,Wang S.Rigorous derivation of incompressible e-MHD equations from compressible Euler-Maxwell equations.SIAM J Math Anal,2008,40:540-565
[21]Peng Y J,Wang S.Asymptotic expansions in two-fluid compressible Euler-Maxwell equations with small parameters.Discrete Contin Dyn Syst,2009,23:415-433
[22]Peng Y J,Wang S,Gu Q L.Relaxation limit and global existence of smooth solution of compressible Euler-Maxwell equations.SIAM J Math Anal,2011,43:944-970
[23]Rishbeth H,Garriott O K.Introduction to Ionospheric Physics.Academic Press,1969
[24]Stein E M,Singular Integrals and Differentiability Properties of Functions.Princeton Mathematical Series. Princeton:Princeton University Press,1970
[25]Ueda Y,Kawashima S.Decay property of regularity-loss type for the Euler-Maxwell system.Methods Appl Anal,2011,18:215-268
[26]Ueda Y,Wang S,Kawashima S.Dissipative structure of the regularity type and time asymptotic decay of solutions for the Euler-Maxwell system.SIAM J Math Anal,2012,44:2002-2017
[27]Wang S,Feng Y H,Li X.The asymptotic behavior of globally smooth solutions of bipolar non-isentropic compressible Euler-Maxwell system for plasm.SIAM J Math Anal,2012,44:3429-3457
[28]Wang S,Feng Y H,Li X.The asymptotic behavior of globally smooth solutions of non-isentropic Euler-Maxwell equations for plasmas.Appl Math Comput,2014,231:299-306
[29]Xu J.Global classical solutions to the compressible Euler-Maxwell equations.SIAM J Math Anal,2011,43:2688-2718
[30]Yang J W,Wang S.The diffusive relaxation limit of non-isentropic Euler-Maxwell equations for plasmas. J Math Anal Appl,2011,380:343-353
∗Received October 30,2014;revised February 14,2015.The authors are supported by the Collaborative Innovation Center on Beijing Society-building and Social Governance,NSFC(11371042),BNSF(1132006),the key fund of the Beijing education committee of China and China Postdoctoral Science Foundation funded project.
 Acta Mathematica Scientia(English Series)2015年5期
Acta Mathematica Scientia(English Series)2015年5期
- Acta Mathematica Scientia(English Series)的其它文章
- ON SOLVABILITY OF A BOUNDARY VALUE PROBLEM FOR THE POISSON EQUATION WITH A NONLOCAL BOUNDARY OPERATOR∗
- GENERAL DECAY OF SOLUTIONS FOR A VISCOELASTIC EQUATION WITH BALAKRISHNAN-TAYLOR DAMPING AND NONLINEAR BOUNDARY DAMPING-SOURCE INTERACTIONS∗
- Lp-CONTINUITY OF NONCOMMUTATIVE CONDITIONAL EXPECTATIONS∗
- CONTROLLABILITY AND OPTIMALITY OF LINEAR TIME-INVARIANT NEUTRAL CONTROL SYSTEMS WITH DIFFERENT FRACTIONAL ORDERS∗
- A MATHEMATICAL MODEL OF ENTERPRISE COMPETITIVE ABILITY AND PERFORMANCE THROUGH EMDEN-FOWLER EQUATION FOR SOME ENTERPRISES∗
- SOLUTIONS TO NONLINEAR ELLIPTIC EQUATIONS WITH A GRADIENT∗
