磨光集及其应用

刘保乾

（西藏自治区组织编制信息管理中心，西藏拉萨850000）

磨光集及其应用

刘保乾

（西藏自治区组织编制信息管理中心，西藏拉萨850000）

提出了磨光集的概念，并详述了计算磨光集的算法和程序；讨论了磨光集在发现不等式、三角形不等式分拆证明及在量级研究中的应用；给出了关于R，r和s的三角形不等式的试探性分拆程序.

磨光集；Bottema软件；agl2012程序；不等式自动发现

0 引言

文献[1]利用随机数验证程序编写了不等式磨光程序，即通过对一个给定的非负表达式集进行打磨，最终达到加强不等式的目的.由于随机数验证程序多数情况下得不到最佳系数的精确值，故文献[1]中的不等式磨光器有局限性.本文通过对优秀机器证明软件Bottema有关确定最佳值的命令进行修改，使不等式自动发现与判定程序agl2012能够以程序方式调用Bottema软件，并得到最佳值，从而实现最佳不等式的自动发现.在文献[1]的基础上，提出了磨光集的概念，并编写了磨光集计算程序，专题讨论了磨光集的若干应用.

1 调用Bottema软件编程

Bottema软件是一款十分优秀的机器证明软件.Bottema软件的作用不仅仅在于它强大的功能，而且还在于它影响了一个研究群体----包括本文作者以及文献[2]和文献[3]等作者在内（暂且不算那些校院内专门从事机器证明研究的众多硕士和博士），都是通过Bottema软件的辐射和引领迈入机器证明之门的.在此对Bottema软件的影响力进行专门强调，不仅不多余而且十分必要，这有助于机器证明的进一步研究，有助于Bottema软件应用潜力的挖掘.

以前人们对Bottema软件的应用，大多停留在较低的层次上，即仅仅使用了Bottema的基本功能，即以输入指令、等待响应的人机交互方式使用软件，而且软件也

没有形成标准的有输入参数和输出参数的功能模块.对此，笔者曾在中国不等式研究小组网站上建议让有关命令设置返回值，以便于应用程序直接调用，以获得更高级的应用形式.虽然目前Bottema软件的版本已经做了一些改进（如判定命令xprove增加了返回值true或false），但在形成标准化模块方面仍显不足.在agl2012程序的应用层面上，由于对Bottema软件的一些功能应用要求十分迫切，在此情况下，笔者对Bottema软件的源程序进行了研读，形成了Bottema软件的一个修改版本，现暂命名为Bottemap，以解决实际问题.Bottemap主要做了如下修改工作：

（1）过滤了有关打印命令，从而使应用程序不再出现Bottema软件的详细提示信息，使运算界面更简洁，并提高了运算速度；

（2）在目前的版本中，由于Bottema软件判定三角形不等式的prove命令不是总能够返回true或false，故用agl2012的代数化命令aptoxp将所有有关表达式代数化，统一用Bottema软件的xprove命令作为证明器，因为在返回值方面，xprove命令比prove命令更完善一些.

（3）在Bottema软件中，用aa表示锐角三角形，为了解决锐角三角形不等式用xprove命令的判定工作，可用aptoxp将约束条件同步代数化，如用aptoxp（cmp（a^2+b^2-c^2））>=0代替条件参数aa，以使用xprove命令的统一格式.

（4）Bottema软件的优越功能之一是能够确定最佳参数或系数（通常是给出关于最佳结果的一个方程式），其主要命令是findmax（三角形）和xmax（代数）.但这些最优化命令均按照便于阅读的形式输出，没有返回值.经分析Bottema软件源程序知，最佳值的最终计算结果在f3参数中，这样将程序中的print f3（打印输出）改为return f3，这样就可以实现由程序方式得到Bottema的计算结果，这为拓展应用创造了条件.

agl2012程序主要应用了Bottema软件的两个功能：一是正性判定功能.由于agl2012程序自动发现的结果是用随机数验证程序测试的，最终要经过证明器判定.在最终结果判定方面，Bottema软件是优先考虑的证明器之一.二是确定最佳系数功能.由于修改后的Bottemap程序可以直接返回计算结果（虽然只是一个关于结果的方程式），这为自动发现最佳不等式创造了条件.

由于3次以上的方程精确根往往不容易得到，故在用agl2012程序调用由Bottema软件计算的最佳值时，常限制在3次方程以下.为了得到惟一的符合条件的解，可结合随机数验证程序进行编程，即如果方程是一次的，则直接求解；如果是二次的，则分两种情况：若一正一负，直接求正根；若两个正，此时可调用随机数验证程序otf直接测试取哪个根时不等式成立.

2 最简集和磨光集

2.1 过滤掉等价的表达式

如果一些表达式，是通过对另一些表达式乘非零常数得到的，则称这些表达式是彼此等价的.如s2-16Rr+5r2，2s2-32Rr+10r2，是彼此等价的.又如，x2+y2+z2-xy-xz-yz，（y+z-2x）2+（z+x-2y）2+（x+y-2z）2，

（y-z）2+（z-x）2+（x-y）2，也是彼此等价的.

在不等式自动发现结果集中，常常有一些结果是等价或重复的，此时需要将其中等价的元素过滤掉，为此需要编写过滤程序ngldj.ngldj的主要语句是：

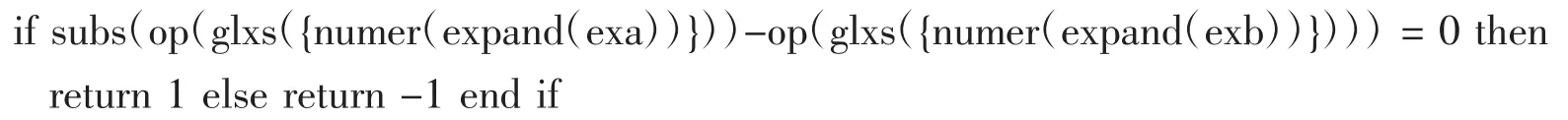
其中glxs的作用是过滤掉一个整系数多项式数据集中每个元素诸项系数的最大公约数.

例1有数据集

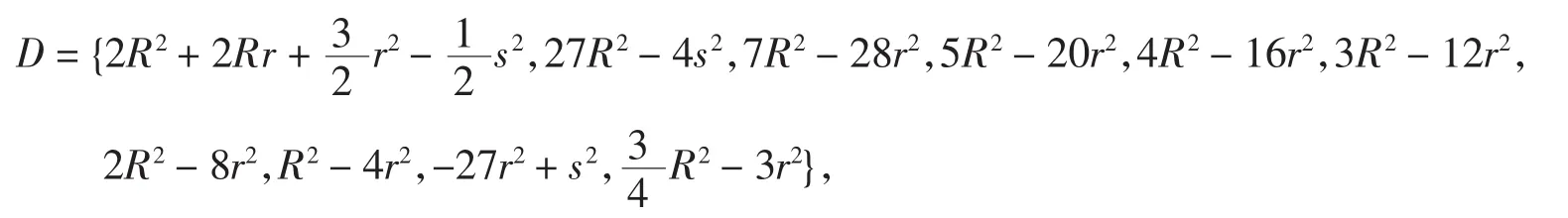
试过滤掉D中的等价元素.

解在读入agl2012程序的Maple环境中，键入命令ngldj（D），立即输出：

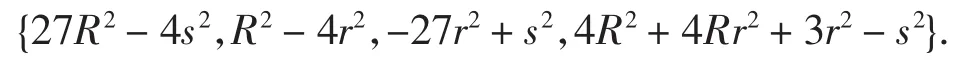
2.2 最简集

两个彼此不等价的半正定表达式f和g，如果存在正数k，使不等式f≥kg成立，则称g能够把f拆开.

设有半正定表达式构成的集合A，且A中的元素互不等价，用ai表示A的元素，n表示A中元素的个数.如果A中的某个元素ai不能被异于自身的其它元素拆开，则称ai为A的最简式.所有A的最简式全体构成A的最简集.现讨论求最简集的算法：考察测试式ei=ai-kaj（1≤i，j≤n，i≠j），对某个具体的i，当1≤j≤n时，如果存在正数k使ei≥0成立，则将ai抛弃，否则将ai存入结果变量J中，直到i取遍不超过n的所有自然数，这样得到的集合J就是A的最简集，记为Z（A）.据此算法就可以编写确定一个集合最简集的程序ljdl.

例2在ΔABC中，确定数据集

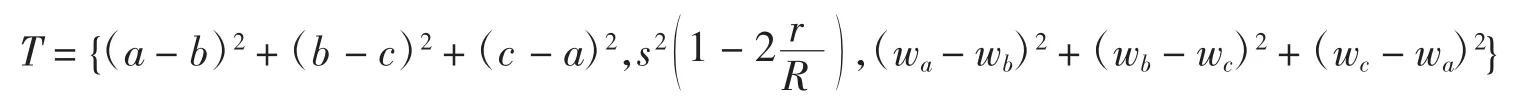
的最简集，其中wa，wb，wc表示三角形内角平分线.

解对数据集T中的每两个元素ti，tj（i，j＝1，2，3），验证是否存在正数k，使不等式ti-ktj>0，如果k存在，则ti即T的非最简式，经测试知，ti（i＝1，2，3）皆非最简式，故Z（T）为空集.

例3在agl2012环境下，键入命令

很快输出J集合的最简集：

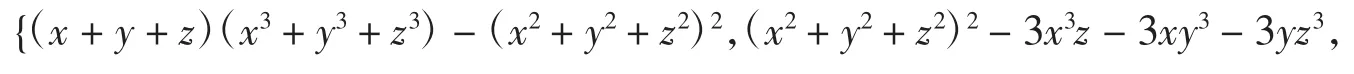
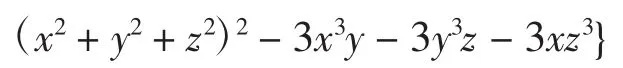
由量级（参阅文献[4]）的定义可知，如果两个表达式不能互相拆开，则这两个表达式的量级是彼此独立的.由此可知，最简集中的元素之间的量级一定是彼此独立的.而一个数据集中各元素的量级如果相等，则这个数据集的最简集必是空集.

2.3 磨光集

以下叙述的算法类似于文献[1]中的磨光器算法，但也有所变化.

在上面讨论最简集时，对于集合A和（1）式，如果正数k存在，则将ai抛弃了，其实，对于不等式

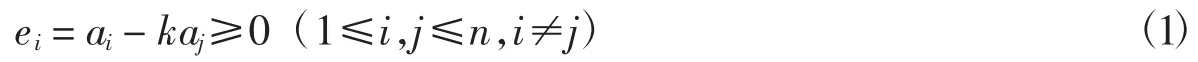
来说，可以借助Bottema软件计算最佳kmax.用反证法结合量级的定义易证，E（ai-kmaxaj）是一个异于E（ai）和E（aj）的新量级.由此可得到不同于最简集的另一种算法：在不等式（1）中，对某个具体的i，当1≤j≤n时，如果正数k存在，则计算最佳k，并将aikmaxaj存入结量变果A1中，否则将ai存入A1中，直到i取遍不超过n的所有自然数，称这个过程为对集合A进行了一次打磨.很显然，还可以对A1继续进行打磨，如此循环，直到得到的集合中的元素数目不再发生变化为止.称最后得到的集合为集合A的磨光集，记为G（A）.显然对磨光集进行一次打磨将得到其自身.

在不等式（1）中，如果最佳系数kmax是一个高次方程的根，此时ai-kmaxaj将无法精确表示，在实际研究中，这种情况要舍弃，如此得到的磨光集称为集合A的不完全磨光集.在实际编程中，当用Bottemap软件的xmax命令计算出最佳系数所在的方程后，判断是否为2次以下，以得到精确表达式，这样就可编写出计算不完全磨光集的程序（简称为磨光器）.由于磨光集的实际计算很费时，为了减少数据量，下面给出一个简化算法，即在不等式（1）中，保证aj总在Z（A）中取值，ai总在A-Z（A）中取值，从而得到磨光器botkmgq.磨光器botkmgq的算法包括两部分，即BOTK和BOTKMGQ.

算法BOTK：

B1.输入一个没有等价元素的数据集expr；

B2.计算expr的最简集Z（exp r），并置入集合变量exa中；从expr中取掉exa，并放入变量exb中；

B3.用exb中的元素exb[i]和exa中的元素exa[j]建立不等式exb[i]-kexa[j]≥0，调用Bottema确定最佳值命令计算最佳k所在的方程，如果方程是一次式，则解出k，从而得到半正定式exb[i]-kexa[j]，将这个表达式收集在temp变量中，直到下标i跑遍exb中的所有元素、下标j跑遍中exa的所有元素为止.

B4.将temp与最简集合并Z（exp r），即执行语句temp:=temp union exa；

B5.输出temp.

算法BOTKMGQ：

L1.输入一个没有等价元素的数据集ex，并将这个数据集置入变量tempb中；

L2.计算botk（tempb），并将计算结果置入变量tempa中；

L3.过滤tempa中的等价元素，即作赋值运算tempa:=hjxs（tempa），并比较tempa和tempb集合；

L3.1如果tempa和tempb相同，则输出tempa，停机；

L3.2如果tempa和tempb不相同，则计算botk（tempa），并将计算结果置入变量tempb中，转向L2.

注1在BOTKMGQ算法中，过滤掉tempa中的等价元素是十分必要的，否则将会造成磨光集中的元素丢失.

例4设x，y，z≥0，LD＝{（x+y+z）3-3（x+y+z）（xy+zx+yz），（x+y+z）3-27xyz，3（x+y+z）（x2+y2+z2）-（x+y+z）3}，试求G（LD）.

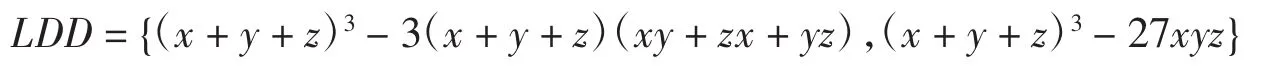
则有G（LD）=G（LDD），用Bottema软件验证知，有最佳不等式

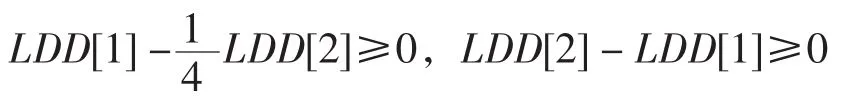
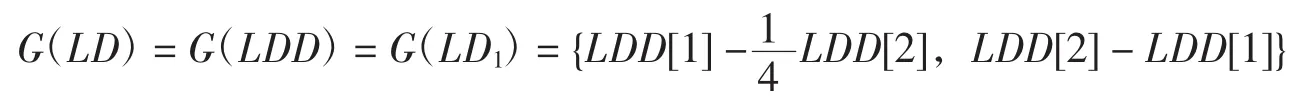
化简系数，得

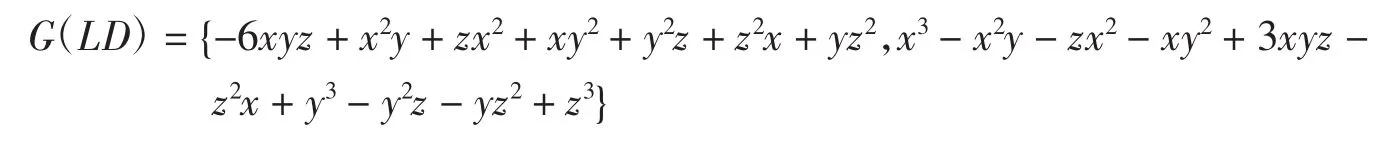
例5试说明数据集

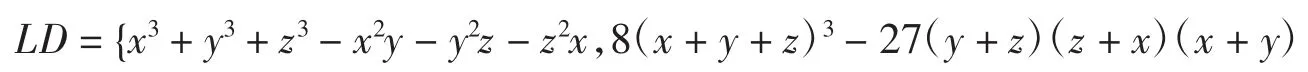
的磨光集不可精确表示出来.

解用Bottema软件验证知，不等式LD[1]≥kLD[2]中的最佳k为方程

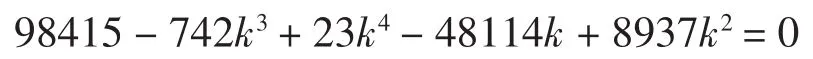
的一个实根，而这个方程的根不可精确表示，故LD的磨光集不可精确表示出来.

当集合中的元素较多时，计算磨光集十分费时，甚至不可能计算，此时可以考虑将集合分割为若干子集，再计算子集的磨光集.设A=A1∪A2…∪An，计算

T和G（A）是怎样的关系很有趣.以（2）式为依据，可编写分块计算（部分）磨光集的程序botkmgqcut.

即使采用了分块策略，也常常计算时间超长，而得不到最终磨光集，此时可考虑设置一些中间变量（如tempa）为全局变量，以传出中间计算结果，这样做，至少从发现新不等式的角度也是可取的.

注2由例5知，磨光集通常是不可以精确表示出来的，故平时研究所得的通常是某个集合的不完全磨光集，在不致误解的情况下，也为了方便，通常笼统的称为磨光集，而省略了“不完全”三个字.

3 磨光集的应用

3.1 发现不等式

例6键入命令：

则输出优美不等式

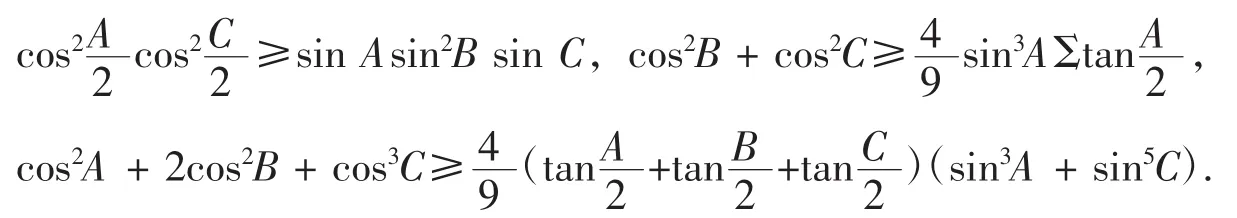
3.2 发现恒等式

由于磨光集中的元素均是最简式，故磨光集中的不等式也是（相对于数据集）最佳不等式，当然在磨光集中也会出现最佳不等式的另一种形式--恒等式.

例7键入命令：

经过3 767.094 s运算，输出两个量级彼此独立的多项式

同时，输出5 237个恒等式.但这些恒等式中，有些是等价的（仅相差一个系数），为此需要用hjxs函数过滤，最后得到1 229个恒等式，如有优美形式：

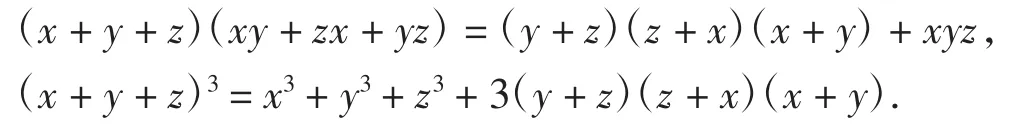
例8以三角形中的表达式作为数据，用磨光器程序可发现优美恒等式

3.3 发现扩展Si类不等式

有特殊零点的多项式历来受到人们的关注，因为这类不等式往往很强.Si类不等式（多项式）是文献[5]定义的，其含义是：n元多项式（不等式）当有n-i个变元相等时取值为零.为了引用方便，也为了把问题归类，文献[6]定义了扩展Si类不等式（多项式），它的含义是：不仅当变元相等时不等式可取到等号，而且当变元成某种比例关系时不等式也可取到等号.由于磨光集是由最佳不等式构成的集合，故磨光集中经常会出现扩展Si类不等式.

例9键入命令：

则运算几个小时后仍不见终止迹象，这时人工中断，显示tempa变量（即显示中间计算结果），其中有7 000多个结果，键入命令：

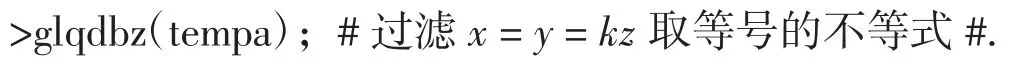
最后输出107个结果，其中有优美形式：

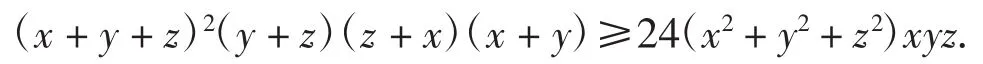
类似可发现三角形中取等号条件为a=b=kc的不等式（扩展Si类不等式），如

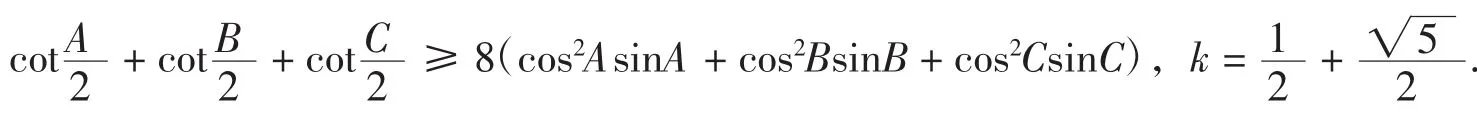
3.4 实现关于R，r和s的三角形不等式分拆证明

三角形中关于半周长s，外接圆周半径R，内切圆半径r的不等式，一般利用基本不等式

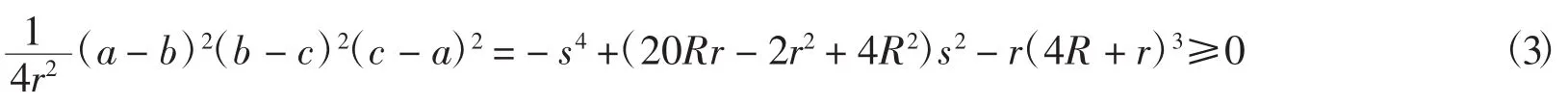
和Gerretsen不等式

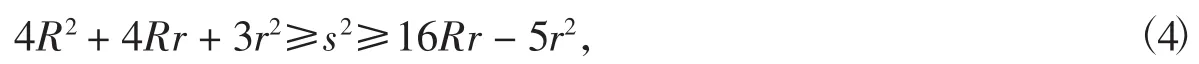
再结合函数的单调性进行证明，而且这种方法十分流行.1999年前后，江苏的褚小光采用了一种方法，这种方法的特点是以不等式（3），（4）及Euler不等式

以及杨学枝不等式

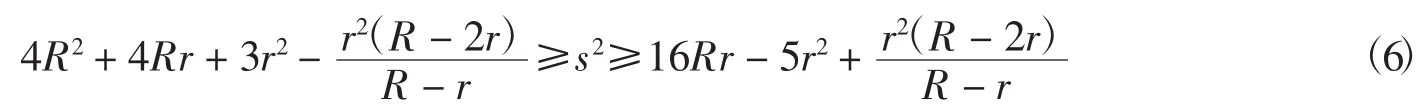
为基础进行分拆证明.1999年，在江苏苏州召开的第二次全国不等式研究学术交流会上，褚先生曾在会议上交流过这种分拆方法，并在中国不等式研究小组内刊《不等式研究通讯》上给出了大量的分拆例子，至此以后，这种s-R-r分拆方法普遍被采用.

在用褚小光的分拆方法证题时，常常会有这种情况：在分拆较弱的不等式时，用不等式（4）和（5）就可以完成，但在分拆较强的不等式时，必须借助于基本不等式（3）和杨学枝不等式（6）.这就给了我们一个暗示：要分拆证明一些不等式，还需要新发现一些更强的不等式.

在以前s-R-r分拆证明中，可见到的例子多是针对s的偶次方情形，对s的奇次方情形很少见到.文献[7]指出，s的奇次方情形有独特的证题意义，但文献[7]没有对此展开讨论.实际上，利用磨光集可以部分解决这个问题，具体思路是：通过agl2012程序的自动发现命令发现关于s-R-r的二次不等式，从而得到数据集，然后计算这个数据集的磨光集，最后以磨光集作为分拆集[8]，再用文献[6]中的算法实现不等式的分拆证明.

例10试建立一个关于三角形中s，R，r的二次不等式分拆集.

解首先用agl2012程序的命令gc_ex（1，2，{s，R，r}）得到表达式

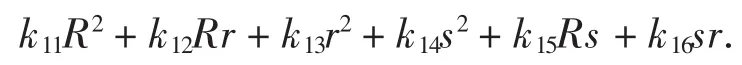
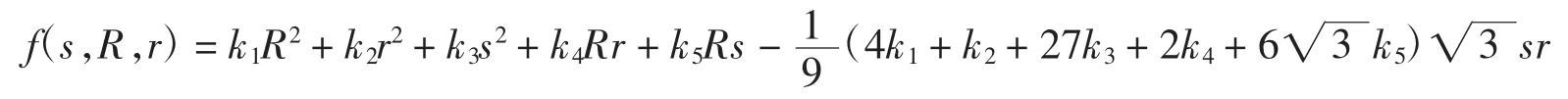
以ki为循环变量，建立程序，从而得到具体系数的表达式，再调用随机数验证程序进行验证，从而发现不等式.为了节约时间，并得到有理系数的不等式，可加入语句：

if has（bds，{sqrt（3）}）=false then…end if.

则经过28 677.188 s运算后输出最佳不等式集F=F1∪F2，其中集合F1中是取等号条件仅为a=b=c的普通不等式，集合F2中是扩展Si类不等式（即取等号条件为a=b=kc的不等式）.

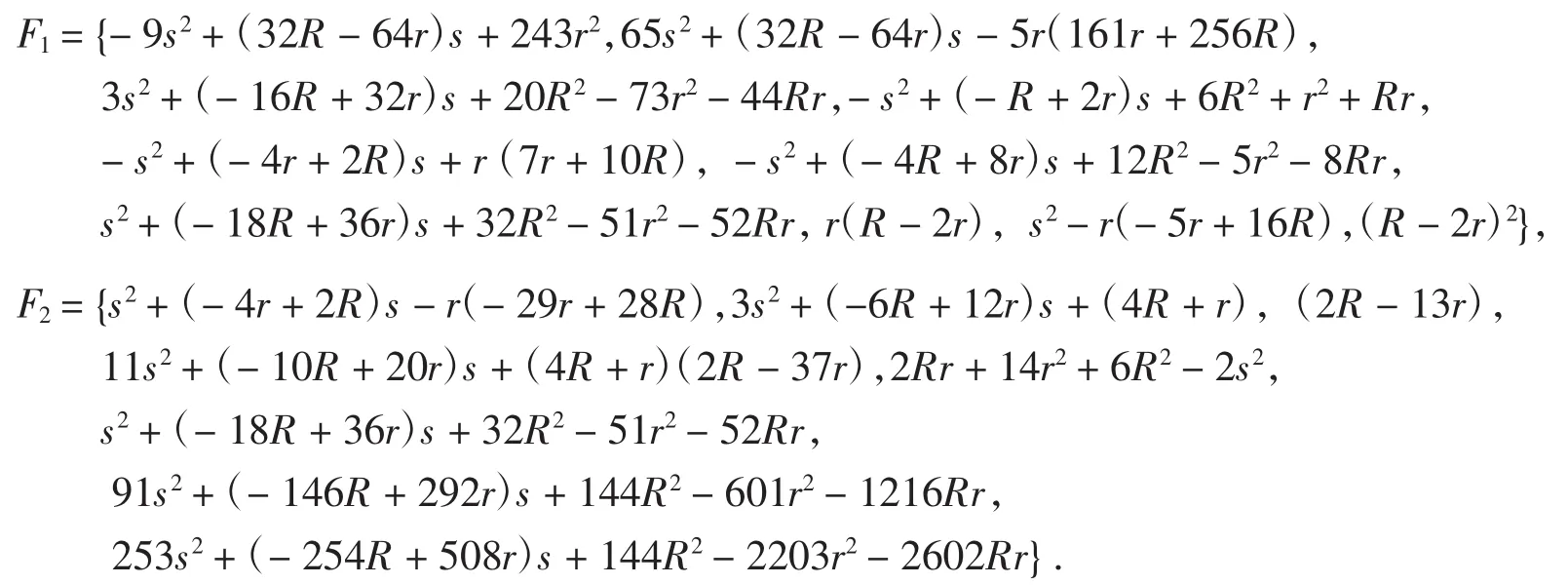
F就是想要得到的分拆集.令人意想不到的是，分拆集F中的不等式能够拆开Gerrsenet不等式（4）的左半部分，即有分拆式：

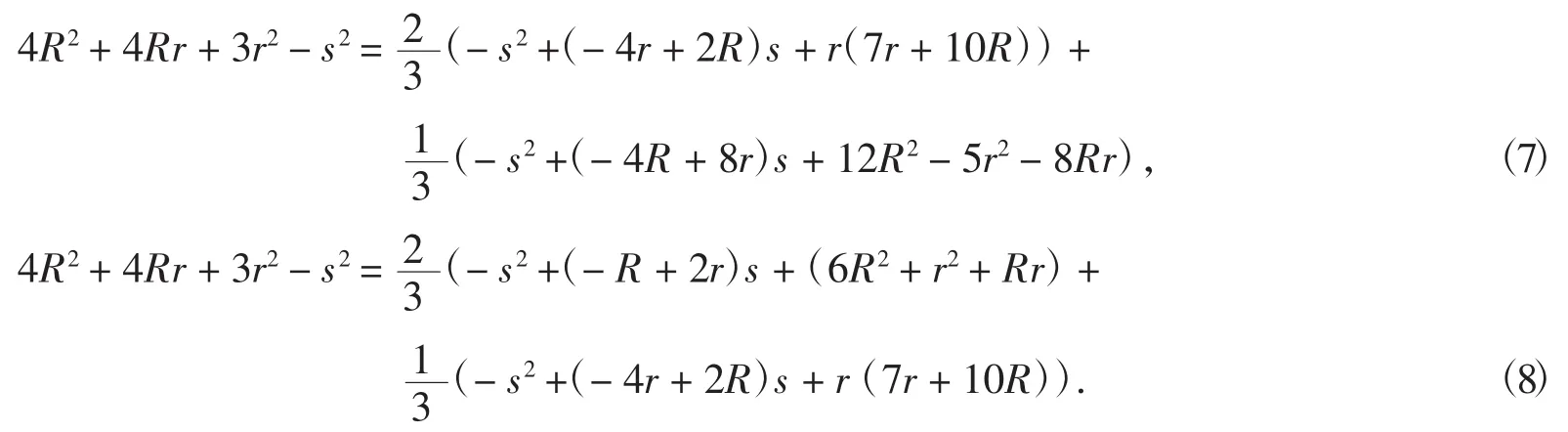
由于分拆单位小了，故能够分拆的范围扩大了.

这样，以F作为分拆集，按文献[6]中的算法，调用文献[9]中的解方程组程序，就可以得到关于R，r与s的三角形不等式的分拆命令tganyfc（一般三角形）和tgrjfc（锐角三角形）.

注3最简式是相对于某个集合而言的，最简集也是相对于某个集合而言的，磨光集同样如此.当磨光集作为分拆集出现时，为了解决更多的问题，相对于的那一个集合通常取的很大，事实上它是已经认知到的不等式的全体.

注4在实际分拆程序中，分拆集F中的元素远比这里的多，它们一方面来自于例10所述的途径（如可将命令tgany2（-10，10）中的系数10改为更大的数，以得到更大的数

据集），另一方面，对平时研究过程中得到的关于s-R-r的二次不等式进行积累，以得到更完备的分拆集.如果一个不等式不能够被F中的元素拆开，则它原则上就可以放入F，成为分拆集中的元素.

注5由文献[10]知，关于R，r与s的二次三角形不等式，总是可以得到人工证明的，这也是笔者选择二次结果作为分拆集的原因.

注6为了能够拆出任意次的关于R，r与s的三角形不等式，分拆集F中还要增加一些线性不等式，这可由复合命令botkkmgq（xhh3_3（-2，2，{R，r，s}，1，1，1，{}，0，0））完成，输出的磨光集是，对于较弱的不等式，为了使拆分形式简洁，也可收入Euler不等式（5），其中即是著名的W.J. Blundon不等式.

注7在构造锐角三角形不等式的分拆集时，既要考虑收入锐角三角形不等式，也要考虑收入任意三角形不等式，除此之外，还要收入一些正的量.如对锐角三角形，考虑约束条件（b2+c2-a2）（-b2+a2+c2）（b2+a2-c2）≥0，由于

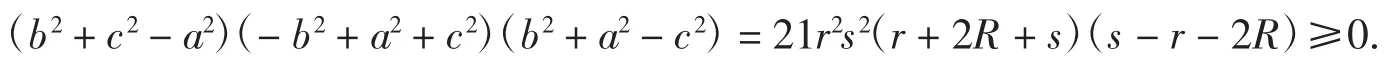
故得到一个正的量s-r-2R，这个线性表达式就要收入到锐角三角形不等式的分拆集中.

下面给出若干实际分拆的例子.

例11试证明分拆集F中的不等式g=-s2+（-4r+2R）s+r（-5r+16R）≥0.

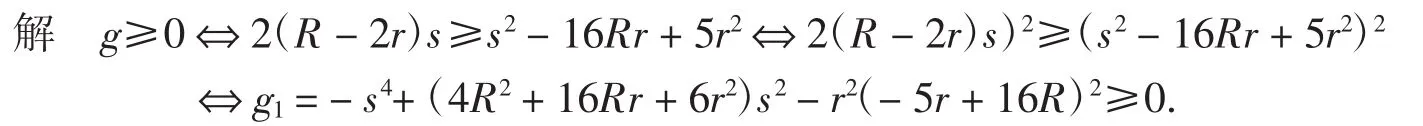
键入命令tganyfc（g1，2，4），则输出

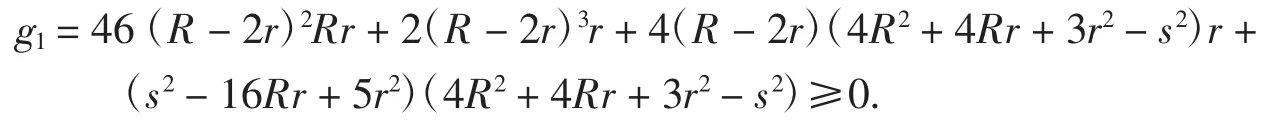
例12笔者曾提出并证明三角形中的优美不等式

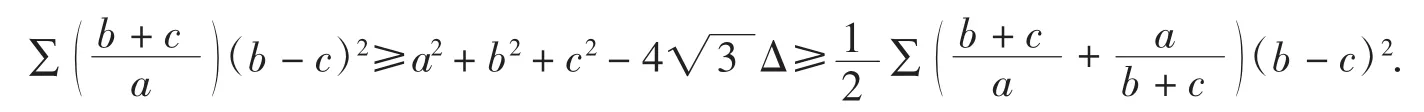
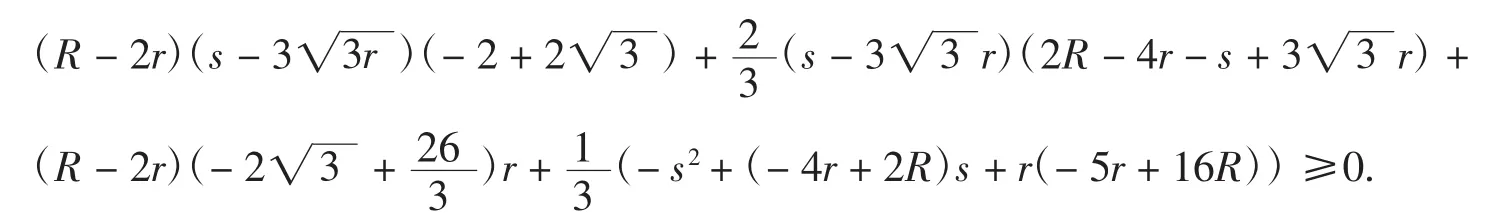
同理，用tganyfc命令可证得不等式链左边，限于篇幅，此略.

3.5 实现量级分拆

由于磨光集中的各元素之间的量级是彼此独立的，故可以用其实现量级分拆，并发现新的量级.

所谓量级分拆，是指对量级P，如果存在量级A和B，满足P=A+B，且量级A和量级B彼此独立（不分大小），则称对量级P进行了分拆，且分拆式是P=A+B.

解法1由tganyfc命令易得分拆式

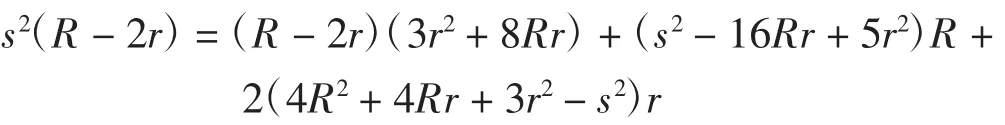
给上恒等式两边取量级得

由于E（（R-2r）r）和E（（s2-16Rr+5r2））是两个彼此独立（不分大小）的量级，故L3的分拆式是

解法2 L3的分拆式的另一个分拆式是（这里省略了分拆过程）；

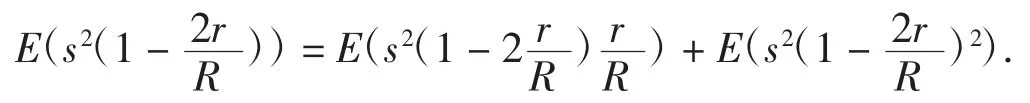
由例13可知，一个量级的分拆式是不惟一的.

例14设三角形ΔABC的三条中线是ma，mb，mc，求E（mambmc）.

解mambmc是一个正的量，而程序tganyfc只能拆非负量，如何解决？可以通过建立相应的不等式解决.事实上，有不等式y=ma2mb2mc2-729r6≥0，易证

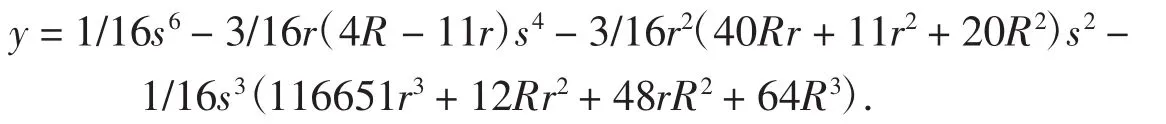
用tganyfc命令可拆得

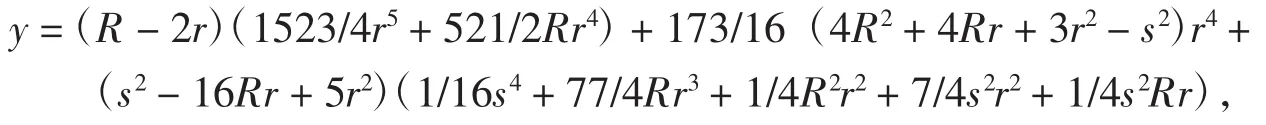
上式两边取量级并化简得（有关过程略）

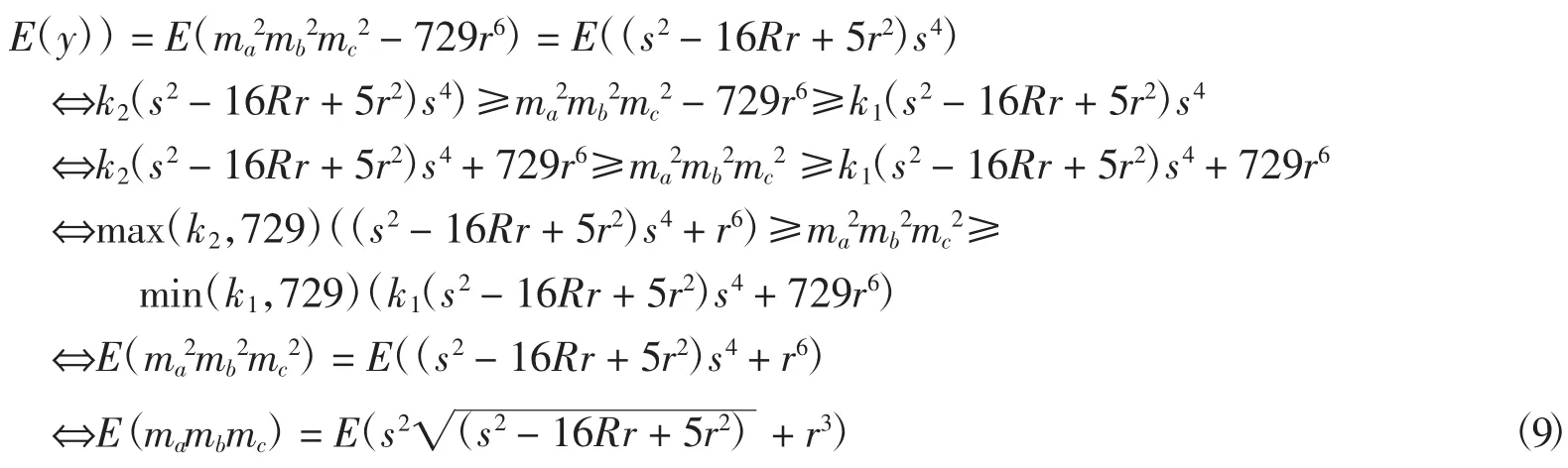
从而求得E（mambmc）.比较文献[12]中例6中的结果，得优美量级恒等式

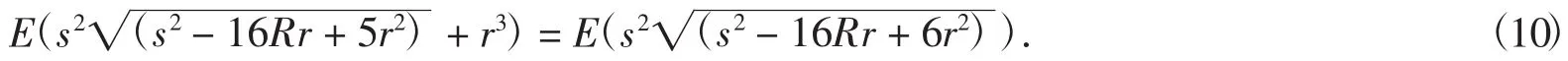
由恒等式（9），（10）可知，量级E（mambmc）一方面可以看成是非负量级

注8对正的几何量，通过建立等腰三角形时取等号的不等式确定量级，是一个普遍且实用的方法.

例15试建立一个关于三角形R，r与s的二次量级库.

解分四步建立：

a.要建立一个量级库，首先要有大量的非负表达式，以便从中采集量级；其次，要保证库中的量级不重复.由于agl2012程序有丰富的不等式自动发现命令，故第一个问题容易解决.而要保证量级不重复，就要设计量级过滤器gllj.程序gllj的设计要依据量级的定义编写，即要测试量级恒等式E（a）=E（b）是否成立，只需测试不等式ak1b≥0，b-k2a≥0同时成立即可.由于在（1）式中，当系数k最佳时，E（ei）既不同于E（ai），也不同于E（aj），即在对集合A的磨光过程中，一直在产生新的量级，所以在算法BOTKMGQ中，对L1步骤中的tempb变量和L3步骤中的tempa施行过滤命令gllj，并用专门的变量进行收集，这样就可以采集到集合A在磨光过程中产生的量级.用La标识这些量级集.

c.由文献[11]知，如果量级P和量级Q彼此独立，则P+Q是一个不同于P和Q的新量级.故确认La∪Lb中两两独立的量级，并且求和，从而得到一个新量级集Lc.

La∪Lb∪Lc∪Ld就是所要求的量级库，用LJ标识这个量级库，具体实现程序是mgqlj.量级库LJ有许多应用，限于篇幅，这里不再作讨论.

[1]刘保乾.不等式的自动发现原理及其实现[J].汕头大学学报：自然科学版，2011，26（2）：3-11.

[2]陈胜利，黄方剑.三元对称形式的schur分拆与不等式的可读证明[J].数学学报，2006，49（3）：491-502.

[3]姚勇.基于列随机矩阵的逐次差分代换与正半定型的机械化判定[J].中国科学（数学），2010，40（3）:251-264.

[4]刘保乾.用对称性和量级研究三角形中的非负对称量[C]//杨学枝.不等式研究（第1辑）.西藏人民出版社，2000：200-222.

[5]刘保乾.类多项式初探[J].广东教育学院学报，2007，27（5）：6-13.

[6]刘保乾.多项式非负分拆算法的若干改进和补充[J].汕头大学学报：自然科学版，2013，28（3）：18-28.

[7]刘保乾.不等式自动发现与判定程序agl2012功能的若干拓展[J].广东教育学院学报，2014，34（5）：28-35.

[8]刘保乾.随机数验证程序在多项式非负分拆中的应用[J].汕头大学学报：自然科学版，2012，27（3）：27-37.

[9]隋振林.一个求线性方程组非负解的通用程序[J].广东教育学院学报，2014，33（3）：32-35.

[10]陈胜利.关于，与的锐角三角形不等式[C]//单墫.几何不等式在中国.南京：江苏教育出版社，1996：72-81.

[11]林新群.三角形中两个非负对称量之和的量级[J].佛山科学技术学院学报：自然科学版，2009，26（1）：28-31.

[12]张小明.三角形二次一阶量级大小的划分[C]//杨学枝.不等式研究（第1辑）.拉萨：西藏人民出版社，2000：223-230.

Burnishing Set and Its App lications

LIU Baoqian
（Information Management Center,Department of Organizational Information,Lasa 850000, Xizang Autonomous District,China）

The concept of burnishing set is proposed.Algorithms and programs for calculating burnishing set are detailed.The applications of burnishing set in the decomposition proofs of inequalities，triangular inequalities are discussed.The applications of burnishing set in magnitude studies are also discussed.Testing decomposition programs for triangular inequalities of R，r and s are given.

burnishing set；Bottema software；program Ag12012；automatically finding of inequalities

O 122.3

A

1001-4217（2015）02-0044-12

2014-12-15

刘保乾（1962-），男，陕西凤翔人，西藏组织编制信息管理中心工作人员.E-mail：wshr987@163.com