基于Schur引理证明方法的矩阵酉三角化

基于Schur引理证明方法的矩阵酉三角化

鲜思东，薛文婷，卢崇霞，罗海燕

(重庆邮电大学理学院，重庆 400065)

摘要：在Schur引理3种证明方法的基础上，给出了矩阵酉三角化的3种方法.

关键词：Schur引理；酉矩阵；三角化

文章编号：1007-2985(2015)05-0001-06

收稿日期：2014-12-20

基金项目：重庆市研究生教育教学改革项目(YJG143010，YJG133006，YJG142009，YJG152016，1202033)；重庆邮电大学校级教学研究项目(XJG1328)

作者简介：鲜思东(1971—)，男，四川南部人，重庆邮电大学理学院教授，硕士生导师，主要从事统计分析建模与不确定优化决策等研究.

中图分类号：O151.21文献标志码：A

DOI:10.3969/j.cnki.jdxb.2015.05.001

1　预备知识

定义1 [1-3]设A,B∈Cn×n(或Rn×n)，若存在U∈Un×n(或En×n)，使得UHAU=U-1AU=B(或UTAU=U-1AU=B)，则称A酉相似(或正交相似)于B.

引理1 [3]n阶λ-矩阵A(λ)与B(λ)等价的充要条件是它们的秩相等和有相同的初等因子.

引理2 [3]设A,B是2个n阶数字矩阵，则A～B的充要条件是(λE-A)≃(λE-B).

引理3 [3-4]设A∈Cn×n，A的初等因子为(λ-λ1)n1,(λ-λ2)n2,…,(λ-λs)ns，则A～J.其中，

引理4上(下)三角可逆矩阵的逆矩阵也是上(下)三角矩阵.

引理52个上(下)三角矩阵的乘积还是上(下)三角矩阵.

2　Schur引理的3种证明方法

下面，先给出Schur引理，再给出3种证明方法：数学归纳法、特征向量法和若当矩阵法.

定理1 [3] (Schur引理)任何一个n阶复矩阵A酉相似于一个上(下)三角矩阵.

证明方法1(数学归纳法)[3]当n=1时，定理1显然成立.

令U1=(α1,α2,…,αk)，则显然U1是一酉矩阵，且

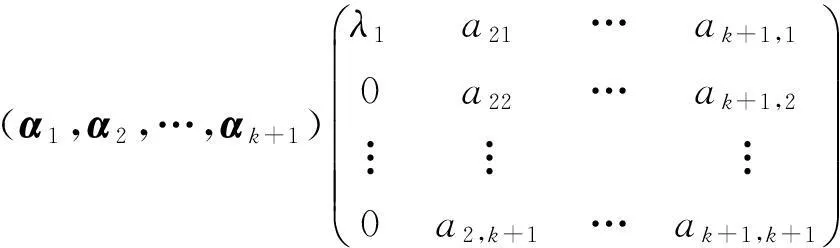
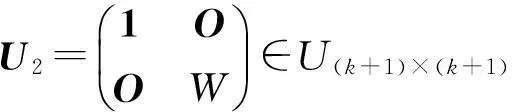
方法2(特征向量法)设A的特征值为λi，特征子空间Vλi的基为αi1,αi2,…,αisi，i=1,2,…,r.

令P1=(α11,α12,…,α1s1,…,αr1,αr2,…,αrsr),则

①当A的这n个线性无关的特征向量是Cn的一个标准正交基，即P1∈Un×n时，定理1成立；

②当A的这n个线性无关的特征向量不是Cn的一个标准正交基，即P1∉Un×n时，应用Schmidt正交化方法将得到Cn的一组标准正交基β1,β2,…,βn，并且α11,α12,…,α1s1,…,αr1,αr2,…,αrsr与β1,β2,…,βn满足

(β1,β2,…,βn)=(α11,α12,…,α1s1,…,αr1,αr2,…,αrsr)Q，

其中Q是以上三角可逆矩阵.

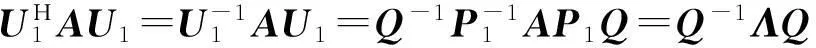
AP1= (Aα11,Aα12,…,Aα1s1,…,Aαr1,Aαr2,…,Aαrsr,Aαm+1,…,Aαn)=

(λ1α11,λ1α12,…,λ1α1s1,…,λrαr1,λrαr2,…,λrαrsr,Aαm+1,…,Aαn).

其中

所以

(1)当α1,α2,…,αn是Cn的一组标准正交基时，由于Jordan矩阵J已经是上三交矩阵了，因此定理1得证.

(2)当α1,α2,…,αn不是Cn的一组标准正交基时，应用Schmidt正交化方法将得到Cn的一组标准正交基β1,β2,…,βn，并且α1,α2,…,αn与β1,β2,…,βn满足(β1,β2,…,βn)=(α1,α2,…,αn)Q，其中Q是以上三角可逆矩阵.

令U=(β1,β2,…,βn)，则U=PQ，故UHAU=U-1AU=Q-1P-1APQ=Q-1JQ=B.由引理4和引理5知，B是一上三角矩阵.

3　基于Schur引理的矩阵酉三角化

在用上述3种方法证明Schur引理的过程中，其实也给出了寻找酉矩阵U的过程.下面，通过一个例子详细介绍运用3种方法将矩阵三角化的过程.

解方法1(数学归纳法)

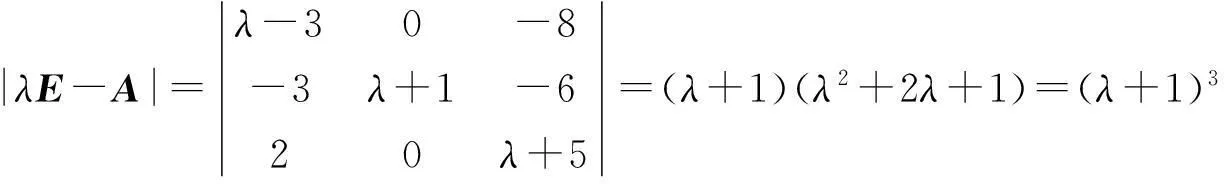
于是，得其特征值为λ1=λ2=λ3=-1.

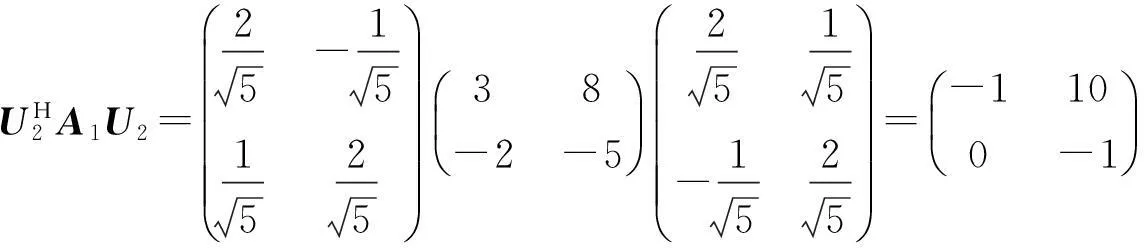
令

方法2(特征向量法)

方法3(若当矩阵法)

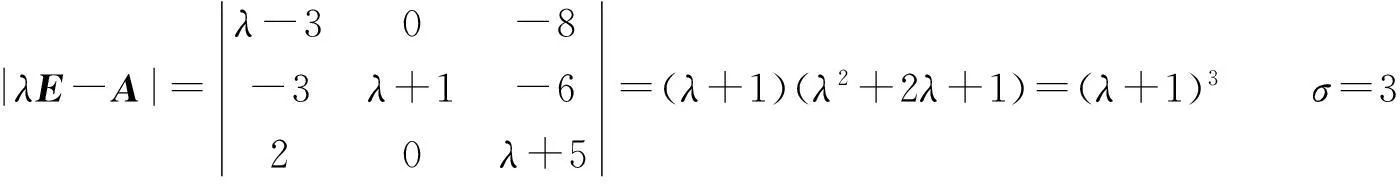
当λ=-1时，

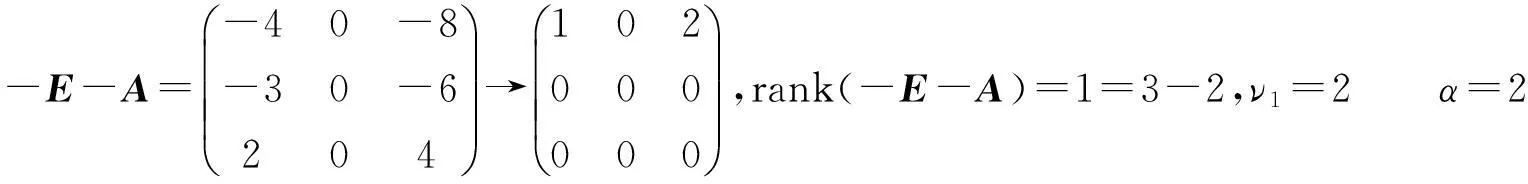
计算结果为ν0=0,ν1=2,ν2=3,m0=2.

基于此，A的属于(σ=3)重特征值λ的有广义特征向量组分块如表1所示.

表1　矩阵A的属于(σ=3)重特征值λ的广义特征向量分块

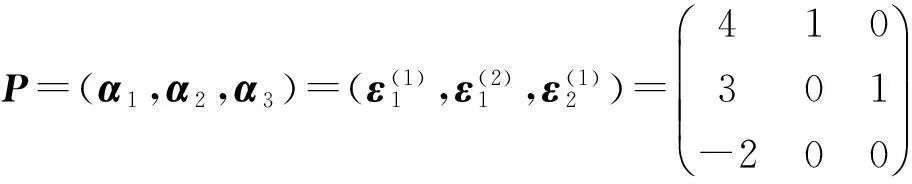
因此

通过例1可以看出，3种方法均能求出将矩阵A上三角化的酉矩阵U，但存在一些区别和联系.具体为：

(1)通过不同的方法找到的酉矩阵U有可能不相同，并且上三角矩阵也可能不相同；

(2)通过相同的方法找到的酉矩阵U也可能不相同，得到的上三角矩阵也会不相同.

不论利用哪种方法找到的酉矩阵U，使得UHAU是上三角矩阵，这些上三角矩阵对角线上的元素是相同的，都是A的特征值，并且λi(i=1,2,…,r)的个数为它的代数重数.

参考文献:

[1]王炎生，陈宗基.基于系统矩阵实Schur分解的集结法模型降阶[J].自动化学报，1996,22(5):560-597.

[2]TSIT-YUENLAM.AFirstCourseinNoncommutativeRings[M].Berlin：NewYork:Springer-Verlag，2001.

[3]史荣昌，魏丰.矩阵分析[M].第3版.北京：北京理工大学出版社，2010.

[4]袁晖坪,陈尚杰.酉对称矩阵的Schur分解[J].西南大学学报：自然科学版，2012(10):12-15.

Unitary Triangularization for Matrix Based on Schur Lemma

XIAN Sidong,XUE Wenting,LU Chongxia,LUO Haiyan

(School of Mathematics and Physics，Chongqing University of Posts and Telecommunications,Chongqing 400065,China)

Abstract:This paper gives the three methods of the unitary triangularization matrix based on the three proving methods of Schur lemma.

Key words:Schur lemma;unitary matrix;triangularization

(责任编辑向阳洁)