完全图的谱

李映辉 ，王守峰

(1.昆明学院数学系，云南昆明650224;2.北京大学数学学院，北京100871;3.云南师范大学数学学院，云南昆明650092)

图谱理论是图论研究的一个活跃而重要的领域，它在量子化学、统计力学、计算机科学、通讯网络以及信息科学中均有着广泛的应用.在图谱论中，图与多种矩阵自然地结合在一起，如邻接矩阵、关联矩阵、拉普拉斯矩阵、无符号拉普拉斯矩阵和距离矩阵等.完全图是图论中一类基础而重要的图，其结构的特殊性导致了它的研究方法的差异性及其结果的简洁性.

本文首先介绍了完全图Kn的邻接矩阵、拉普拉斯矩阵、无符号拉普拉斯矩阵;然后通过组合数学和矩阵论的方法获得了完全图的特征多项式及其邻接谱，即是包含图论信息的代数结构;最后，研究了完全图的特征多项式的系数与图的结构之间的关系，证明了完全图的邻接谱、拉谱拉斯谱和无符号拉谱拉斯三者之间的关系.

1 基本概念

设图Γ的顶点集VΓ是集合{v1，v2，…，vn}，边集EΓ作为顶点集VΓ的无序对的集合，如果{vi，vj}在边集EΓ中，就称vi与vj是邻接的.完全图Kn是一个有n个顶点且相异顶点均互相邻接的图.

定义1［1］图Γ的邻接矩阵是一个n×n矩阵A=A(Γ)，它的元素满足

从邻接矩阵A的定义可直接得到其是一个实对称阵，A的迹为trace(A).由于矩阵A的行和列对应图Γ标记后的顶点，研究邻接矩阵的性质就是研究行列置换后的不变量，即邻接矩阵A的谱的性质.设变量λ是矩阵A的特征值，由于A是实对称阵，故λ是实数，作为方程det(λI－A)=0的根λ的重数是对应λ的特征向量空间的维数.

定义2［1］邻接矩阵A的特征多项式det(λΙ－A)称为图Γ的特征多项式，记为χ(Γ;λ)，A=A(Γ)的特征值也称为图Γ的特征值.

定义3［1］图Γ的邻接谱是A(Γ)的特征值和它们各自重数的集合.若A(Γ)的特征值是λ0＞λ1＞…＞ λs－1，它们的重数分别是 m(λ0)，m(λ1)，…，m(λs－1)，记 A(Γ)的邻接谱为

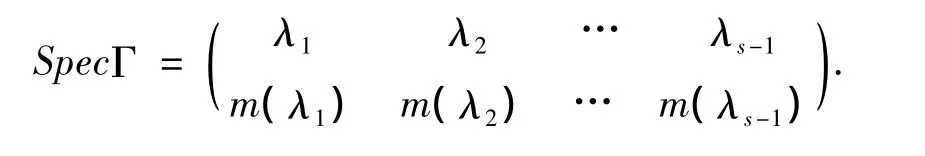
定义4［1］设A是一个矩阵，A的谱展是s(A)=maxij{|λi－ λj|}.

其中max是指取遍邻接矩阵A的所有特征值.

定义5［2］设Γ是一个没有自环的无向图.图Γ的拉普拉斯矩阵L(Γ)的指标是图Γ的顶点集，且行和为0.其中Lxy=－Axy，当x≠y.设D(Γ)是一个指标是图Γ的顶点集，使得Dxy是顶点x的度，则拉普拉斯矩阵L(Γ)=D(Γ)－ A(Γ)，Q(Γ)=D(Γ)+A(Γ)就是无符号矩阵.

在连通图Γ中，连接vi和vj的路径的最少边数称作vi与vj的距离，记作(vi，vj).连通图Γ中距离函数的最大值称作图Γ的直径.

2 预备结论

设图 Γ 的特征多项式是 χ(Γ;λ)= λn+c1λn－1+c2λn－2+c3λn－3+ … +cn，在此公式中－c1是0，即特征值的和，由于A的迹trace(A)，因此c1=0.

引理1［1］图Γ的特征多项式的系数满足:(1)c1=0;(2)－c2是图Γ的边数;(3)－c3是图Γ中三角形数目的两倍.

命题1 图Γ的特征多项式的系数cn具有性质cn=(－1)n|A|.

证明 因为图Γ的特征多项式是χ(Γ;λ)=det|λI－A|，当其变量λ =0，

cn= χ(Γ;λ)=det(λI－ A)=|－ A|=(－ 1)n|A|.

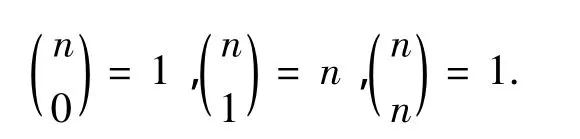
引理2［3］若0≤ r≤n，则

引理3［3］对于所有的整数n和k满足1≤k≤n－1，则

命题2 对于所有的整数n和k满足1≤k≤n－1，则(k－1

证明 根据引理2和引理3，有

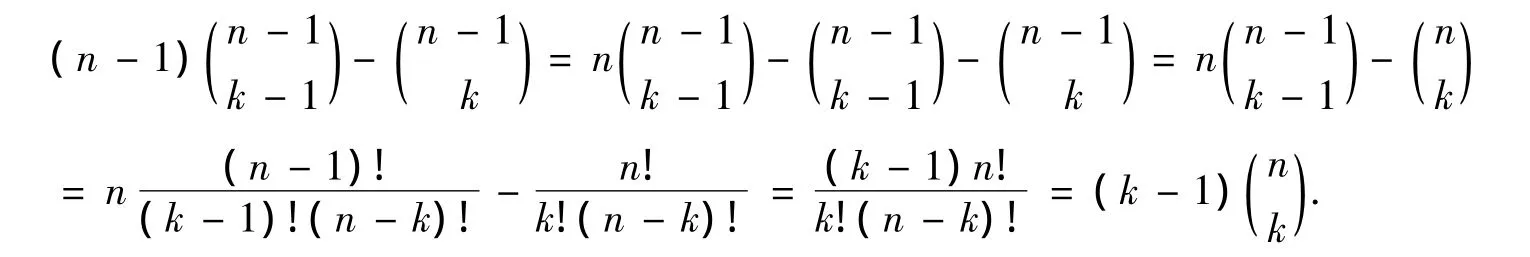
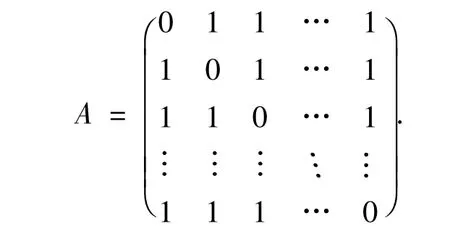
完全图Kn是一个有n个顶点且相异顶点均互相邻接的图，所以自然有完全图Kn的邻接矩阵是

命题3 完全图Kn的特征多项式是 χ(Kn，λ)=(λ －n+1)(λ +1)n－1.

证明

=(λ－n+1)(λ +1)n－1.

由于完全图Kn是k－正则图，即每一个顶点有相同的度k=n－1，根据拉普拉斯矩阵的定义，有完全图Kn的拉普拉斯矩阵

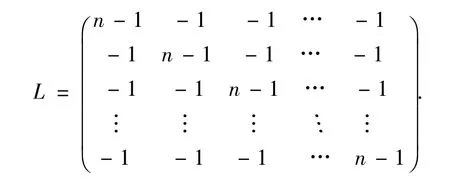
类似完全图Kn的特征多项式，可得到如下命题.

命题4 完全图Kn的拉普拉斯矩阵L的特征多项式是Chapo(L，θ)=θ(θ－n)n－1.

同样的方法可以得到完全图Kn的无符号拉普拉斯矩阵Q，

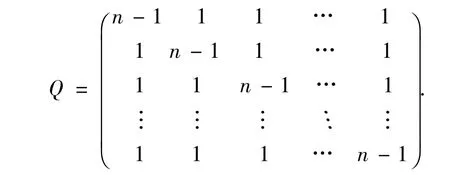
命题5 完全图Kn的无符号拉普拉斯矩阵的特征多项式是

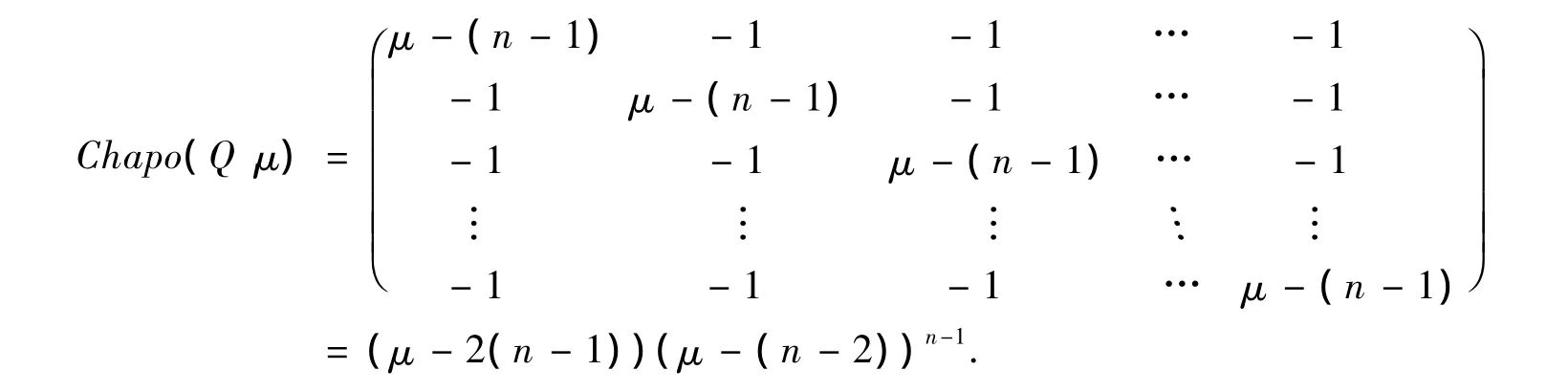
3 主要结果

命题 6 完全图 Kn的特征多项式具有形式 χ(Γ;λ)= λn+c1λn－1+c2λn－2+c3λn－3+ … +cn，其中 ck=

证明 在命题3中给出了完全图的Kn特征多项式，根据命题2有

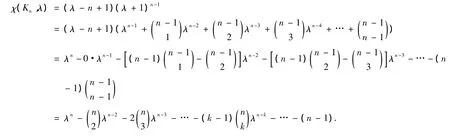
由于完全图有其自身的特殊结构和性质，即每一对相异顶点都是邻接的.根据引理1可知是Kn的边的数目是图Γ中三角形的数目.对于有向图而言是Kn中三角形数目的2倍.另一方面，在命题2中已经有完全图Kn的邻接矩阵的系数的性质，即c1=trace(A)=a11+a22+…+ann=0.当它的变量λ=0时，有cn= χ(Γ;λ)=det(λI－A)=|－A|=－(n－1).

定理1 完全图Kn的特征多项式的系数满足下列性质:(1)c1=0;(2)是Kn中边的数目;(3)是Kn中三角形数目的2倍;(4)－cn=n－1.

在命题3中，完全图Kn的特征值是λ0=n－1，λ1=λ2=… =λn－1=－1，或者说特征值为 －1的重数是n－1.

定理2 完全图Kn的谱是

在矩阵论中已经证明了邻接矩阵的特征多项式的系数c1是A的迹trace(A)，它的所有特征值之和c1=λ0+λ1+… +λn－1=(n－1)－(n－1)=0;特征多项式的系数 cn是所有特征值之积 cn= λ0λ1…λn－1=(－ 1)n－1(n－1).

显然完全图是连通图，所以Kn的直径是1.

引理4［1］设连通图Γ的邻接代数是δ(Γ)，半径是d，那么邻接代数δ(Γ)的维数至少是d+1.

推论 完全图Kn的邻接代数δ(Γ)的维数至少是2，并且有2个不同的特征值.

定理3 完全图Kn的谱展是n.

证明 由于谱展是s(A)=maxij{ λi－ λj}，所以

s(A)=maxij{ λi－ λj}=|λ0－ λ1|=|(n－1)－(－1)|=n.

综合命题3、命题4和命题5，完全图Kn的邻接谱、拉普拉斯谱、无符号拉普拉斯谱分别为

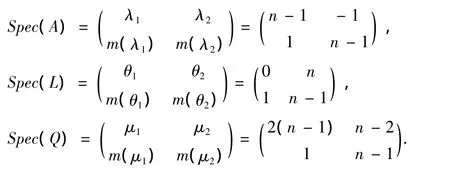
由定理2和以上研究，可得到如下性质.

定理 4 μ1=2λ1=2k，μ2=2λ2+ θ2.

［1］Norman Biggs.Algebraic Graph Theory［M］.Second Edition.London:Cambridge University Press，1993.

［2］Andries E.，Brouwer and Willem H.Haemers.Spectra of Graphs［M］.London:Springer，2012.

［3］Richard Brualdi.Introductory Combinatorics［M］.Fifth Edition.Beijing:China Machine Press，2012.

［4］D.Cvetkovic，S.Simmic.Graph Spectra in Computer Science［J］.Linear Algebra and its Applications，2011(434):1545－1562.