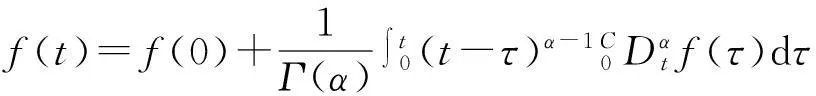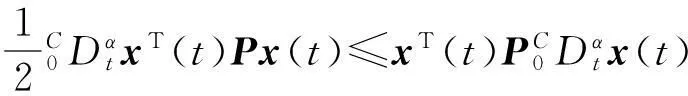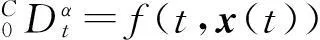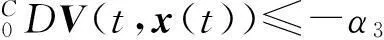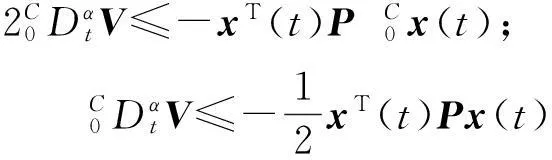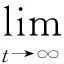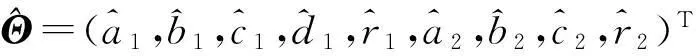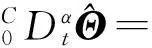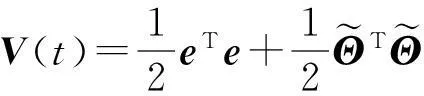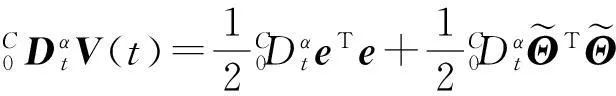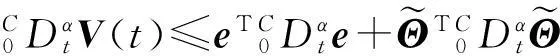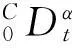带未知参数的分数阶超混沌系统自适应同步控制

李　雄， 李生刚*， 刘　恒,2， 王晓辰

(1 陕西师范大学 数学与信息科学学院, 陕西 西安 710119;

2 淮南师范学院 数学与计算科学系, 安徽 淮南 232038;

3 西安外国语大学 商学院， 陕西 西安 710128)



带未知参数的分数阶超混沌系统自适应同步控制

李雄1， 李生刚1*， 刘恒1,2， 王晓辰3

(1 陕西师范大学 数学与信息科学学院, 陕西 西安 710119;

2 淮南师范学院 数学与计算科学系, 安徽 淮南 232038;

3 西安外国语大学 商学院， 陕西 西安 710128)

摘要：研究了一类带未知参数的分数阶超混沌系统。基于分数阶Lyapunov稳定性理论构造控制器以及分数阶的参数自适应规则，以分数阶超混沌Chen系统和分数阶超混沌Lorenz系统为例实现了同步控制。在分数阶超混沌系统稳定性分析中利用平方Lyapunov函数，提出一个针对含时变系数矩阵的非线性分数阶系统稳定性判定方法，数值仿真结果验证了所提控制方法的可行性。

关键词:分数阶超混沌系统；自适应律；同步控制

分数阶微积分与整数阶微积分几乎有相同长的历史。但是,由于缺乏实际的应用背景及其理论的复杂性, 其理论研究发展相对缓慢[1-3]。随着相关理论的发展，分数阶稳定理论不仅为很多实际系统提供了新的数学工具, 还主要用来描述一些特殊物理系统的动力学行为。在有关物理和化学的复杂系统中，例如光谱分析、漫射、电介质等, 许多专家学者和工程师已经开始应用分数阶微积分来分析解决问题[4-7]。研究发现，在一些复杂的非线性动态系统中, 采用分数阶微积分建立的数学模型比用整数阶建立的数学模型更加精确[8-13]。

随着研究的不断深入，带未知参数的混沌系统的自适应同步问题受到了很多学者的关注，文献[14]利用胡建兵等提出的分数阶混沌系统稳定性理论，研究了参数未知的分数阶超混沌Lorenz系统的自适应追踪控制与同步。文献[15]主要以自治系统为研究对象，研究了线性与非线性系统的自适应广义同步。文献[16]研究了基于线性分离的自治混沌系统的投影同步。此类文献具有一定的可应用性，但是在围绕系统不确定参数给出的自适应同步控制方法的同时，并未考虑外部环境因素对混沌系统某些参数的变动，而这些变动可以造成实际混沌系统与预想设计混沌系统的不一致，控制器鲁棒性不强，难以发挥其应用价值[17-18]。针对该问题，本文在研究带未知参数的分数阶超混沌系统的同步控制问题时，对超混沌系统的一些关键参数进行辨识，并给出了自适应律。

在整数阶系统稳定性分析中主要利用平方Lyapunov函数。文献[2]提出了分数阶系统的Lyapunov第二方法, 该方法给分数阶非线性系统稳定性分析带来了方便，这也使得分数阶非线性系统的控制及稳定性分析逐渐成为研究热点。但是正如文献[7-8]所指, 由于平方Lyapunov函数的分数阶导数具有非常复杂的形式, 在分数阶系统的稳定性分析中使用平方Lyapunov函数是相当困难的, 所以很少有文献成功地运用自适应控制实现分数阶混沌系统的控制或同步。本文主要研究参数未知情况下超混沌系统同步问题，对估计参数设计参数自适应律，实现分数阶超混沌Chen系统和分数阶超混沌Lorenz系统同步，给出能让闭环系统都有界的分数阶自适应律；在稳定分析中成功应用平方Lyapunov函数，并严格证明了系统稳定性；针对带有时变系数矩阵的分数阶非线性系统，提出一个可判定稳定性的推论，方便对该类系统稳定性进行分析。

1分数阶微积分相关理论

分数阶微积分有多种定义，最常用的有以下3种：Grunwald-Letnikov、Riemann-Liouville (R-L)、Caputo。本文采用Caputo的定义,因为Caputo定义中系统的初值和整数阶系统的一样, 具有较好的物理意义。Caputo分数阶微分定义为

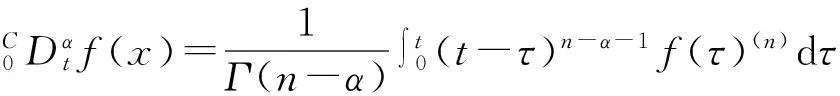
(1)

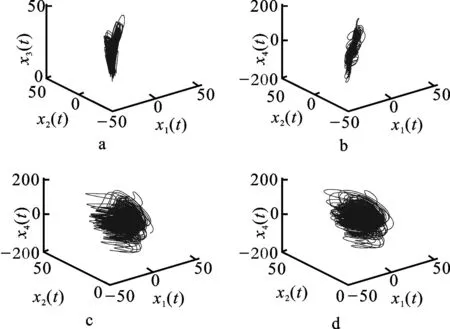
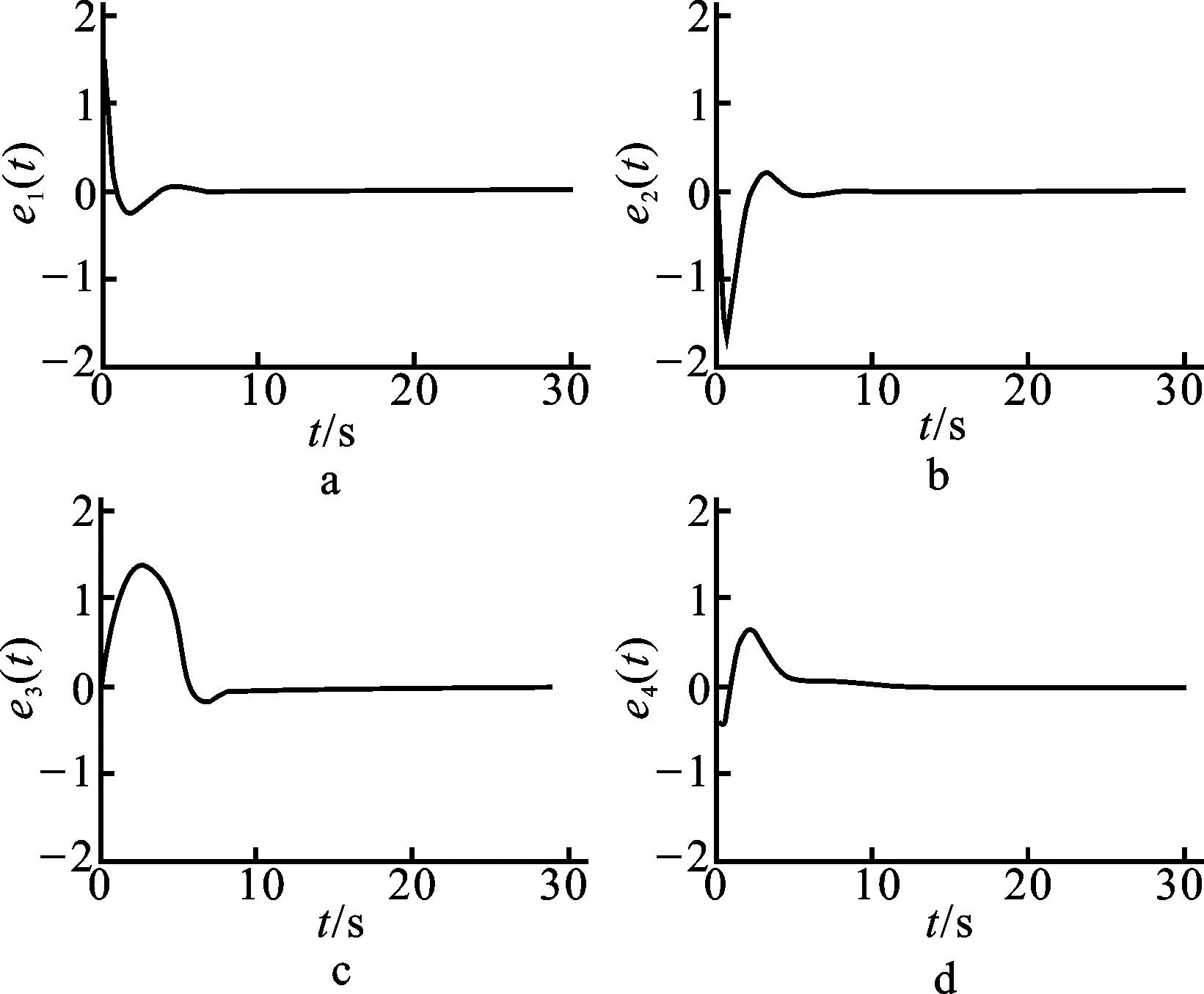
其中，n-1<α

当0<α<1时，Caputo分数阶微分的解等价于

(2)

引理1设x(t)∈Rn且具有连续的一阶导数，则

(4)

其中P为任意的n阶正定矩阵。

(5)

其中x(t)∈Rn为系统变量，f(t,x(t))为满足局部Lipschitz条件的非线性函数。若存在Lyapunov函数V(t,x(t))和K类函数αi(i=1,2,3)使得

则系统(5)渐近稳定。

(6)

其中，0<α<1,A为系数矩阵。若存在实对称正定矩阵P，使得

xT(t)Px(t)=0

(7)

成立，则系统渐近稳定。

证明构造Lyapunov函数如下:

xT(t)Px(t)≤0;

注1推论中分数阶系统方程系数矩阵A可以是常数矩阵也可以是含有变量x的时变矩阵A(t)，这也是对文献[14]的推广。

2稳定性分析及控制器设计

2.1问题描述

(8)

(9)

其中，x(t)、y(t)∈Rn,f、g:Rn→Rn为连续可微的非线性函数，u(t,x,y)为系统的控制输入。

2.2自适应同步控制及稳定性分析

考虑分数阶超混沌Chen系统

(10)

当a1=35,b1=3,c1=12,d1=7,r1=0.5,α=0.95时，此系统是超混沌的[19](如图1)。

图1　分数阶超混沌Chen系统图

受控分数阶超混沌Lorenz系统

(11)

不加入控制变量ui(i=1,2,3,4)时，当a2=10,b2=8/3,c2=28,r2=-1,α=0.95时，此系统是超混沌的(如图2)。

图2　分数阶超混沌Lorenz系统图

将(10)式减去(11)式得到同步误差系统方程

(12)

根据以上讨论可设计控制器u(t)为

(13)

-e4y4)T。

(14)

定理1在给定初始条件下，在自适应控制器(13)、分数阶自适应规则(14)的作用下，可实现超混沌系统(10)和(11)同步，即误差系统(12)渐近稳定。

(15)

(16)

对(12)式两边同时左乘eT，然后把(13)式和(14)式代入(12)式，经过一些简单的推导可以得到

(17)

3数值仿真

为验证本文研究方法的有效性，现对所做结果进行数值模拟。选取分数阶阶次α=0.95，时间步长h=0.01，系统(1)参数选取a1=35,b1=3,c1=12,d1=7,r1=0.5。系统(2)参数选取a2=10,b2=8/3,c2=28,r2=-1。任意选取状态初始值:

x(0)=[0.21-0.150.321]T;

y(0)=[2.131.132.341.51]T;

控制增益G=[3333]T仿真，结果见图3、图4所示。可以看出，按照本文所提出的方法实施控制，可以使误差系统很快地达到稳定状态，从而使得驱动系统和响应系统达到同步。

图3　同步误差曲线图

图4　控制输入曲线图

4结论

基于分数阶Lyapunov稳定性理论设计自适应同步控制器和分数阶参数自适应律，实现了带未知参数的分数阶超混沌系统的同步。成功地利用平方Lyapunov函数的分数阶导数讨论了系统的稳定性，以异结构具有时变结构参数和随机初值的分数阶超混沌Chen系统和分数阶超混沌Lorenz系统为例，设计了主动控制器和参数自适应规则，该方法新颖简单有效，并且很好地解决了参数摄动问题，具有良好的鲁棒性能。数值仿真进一步验证了本文所提方法的有效性。

参考文献：

[1] PODLUBNY I.Fractional differential equations[M]. New York:Academic Press Publishers,1999.

[2] LI Y, CHEN Y Q, PODLUBNY I.Mittag-Leffler stability of fractional order nonlinear dynamic systems[J].Automatica,2009,45:1965-1969.

[3] MATIGNON D.Stability results for fractional differential equations with applications to control processing[J].Computational Engineering in Systems Applications,1996(2):963-968.

[4] LI C P, DENG W H, XU D.Chaos synchronization of the Chua system with a fractional order[J].Physica A, 2006, 360:171-185.

[5] KUNTANAPREEDA S.Robust synchronization of fractional-order unified chaotic systems via linear control[J]. Computers and Mathematics with Applications, 2012, 63:183-190.

[6] CHEN L P, CHAI Y, WU R C, et al.Stability and stabilization of a class of nonlinear fractional-order systems with Caputo derivative[J].IEEE Transactions on Circuits and Systems II:Express Briefs,2012,59(9)：602-606.

[7] YIN C, ZHONG S M, CHEN W F. Design of sliding mode controller for a class of fractional-order chaoticsystems[J].Communications in Nonlinear Science and Numerical Simulation,2012,17:356-366.

[8] WEN X J, WU Z M, LU J G.Stability analysis of a class of nonlinear fractional-order systems[J].IEEE Transactions on Circuits and Syetems II:Express Briefs,2008,55(11):1178-1182.

[9] FALLAHI K, LEUNG H.A chaos secure communication scheme based on multiplication modulation[J].Communications in Nonlinear Science and Numerical Simulation,2010,25:368-383.

[10] MOHAMMAD P A. A Lyapunov-based control scheme for robust stabilization of fractional chaotic systems[J].Nonlinear Dynamics,2014,78:2129-2140.

[11] DU H B,CHENG Y Y,HE Y G,et al. Finite-time output feedback control for a class of second-order nonlinear systems with application to DC-DC buck converters[J].Nonlinear Dynamics,2014,78:2021-2030.

[12] HUANG L L,MA N.A new method for projective synchronization of different fractional-order chaotic systems[J].Acta Physica Sinica,2012,61(16):160501-160506.

[13] RIVERO M, TRUJILLO J,VAZQUEZ L, et al.Fractional dynamics of populations[J]. Applied Mathematics and Computation,2011,218:1089-1095.

[14] 赵灵冬,胡建兵,刘旭辉.参数未知的分数阶超混沌Lorenz系统的自适应追踪控制与同步[J].物理学报, 2010,59(4):2305-2309.

[15] 王兴元,孟娟.自治混沌系统的线性和非线性广义同步[J]. 物理学报2008,57(2):726-730.

[16] 王兴元,王勇.基于线性分离的自治混沌系统的投影同步[J].物理学报,2007, 56(5):2498-2503.

[17] 谭文,李志攀,王耀南,等.一个混沌系统的同步控制研究[J].计算机工程与应用,2011,47(4):219-222.

[18] 李农,李建芬,刘宇平.不确定混沌系统的反同步与参数辨识[J].物理学报,2010,59(9):5954-5958.

[19] YAN Z Y.Controlling hyper chaos in the new hyper chaotic Chen system[J].Applied Mathematics and Computation,2005,168:1239-1250.

〔责任编辑宋轶文〕

Adaptive synchronization control of the fractional order hyper

chaotic systems with unknown parameters

LI Xiong1, LI Shenggang1*, LIU Heng1,2， WANG Xiaochen3

(1 School of Mathematics and Information Science, Shaanxi Normal University,

Xi′an 710119， Shaanxi, China；

2 College of Mathematics and Computational Science, Huainan Normal University,

Huainan 232038， Anhui, China；

3 School of Business, Xi′an International Studies University, Xi′an 710128, Shaanxi, China)

Abstract:Synchronization for a class of fractional order hyper chaotic systems with unknown parameters is studied. Based on the stability theory of fractional order systems and by using the quadratic Lyapunov function, the synchronization controller and recognizing rules are designed for synchronizing the fractional order hyper chaotic Chen system and fractional order hyper chaotic Lorenz system. The final results of the numerical simulation shows that the control method proposed in this paper is feasible.

Keywords:fractional order hyper chaotic system; adaptive law; synchronization control MR subject classification: 93C10

中图分类号：O231.2

文献标志码：A