Nonlocal Symmetries and Interaction Solutions for Potential Kadomtsev–Petviashvili Equation∗

Bo Ren(任博),Jun Yu(俞军),and Xi-Zhong Liu(刘希忠)

Institute of Nonlinear Science,Shaoxing University,Shaoxing 312000,China

1 Introduction

A large number of useful methods have been proposed to find soliton solutions for nonlinear partial differential equations.Some of the most important methods are the inverse scattering transformation,[1]the Hirota’s bilinear method,[2]symmetry reductions,[3]the Darboux transformation,[4]the Painlev´e analysis method,[5]the B¨aklund transformation(BT),[6]the separated variable method,[7]etc.[8]Among these methods,it is still quite difficult to obtain the interaction solutions among different nonlinear excitations.Recently,these interaction solutions were directly obtained by using the localization procedure related with the nonlocal symmetry and a consistent tanh expansion(CTE)method.[9−12]In this paper,we shall apply the localization procedure and CTE method to study the potential Kadomtsev–Petviashvili(pKP)equation.Some interesting results are discussed which might be applicable to explain the relevant physical processes.

The paper is organized as follows.In Sec.2,the nonlocal symmetry for the pKP equation is obtained with the truncated Painlev´e method.To solve the initial value problem of the nonlocal symmetry,the nonlocal symmetry is localized by prolongation the pKP equation.The finite symmetry transformations are presented by solving the initial value problem of the Lie’s first principle.The multi-front waves and the inelastic interactions of two front waves are analyzed by using the finite symmetry transformations.In Sec.3,a CTE method is developed to the pKP equation.It is proved that the pKP equation is CTE solvable system.The CTE method for pKP equation leads to a nonauto-BT theorem.In Sec.4,some special interaction solutions are given due to the entrance of an arbitrary function in the nonauto-BT theorem.The last section is a simple summary and discussion.

2 Nonlocal Symmetry and Multi-front Waves of the pKP Equation

The(2+1)-dimensional pKP equation reads

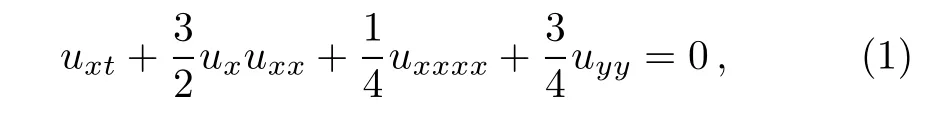
which describes the dynamics in two-dimensional.(1)is derived in various physical contexts assuming that the wave is moving along x and all changes in y are slower than in the direction of motion.[13]Various exact solutions,include traveling wave solutions,linear solitary wave solutions,soliton-like solutions and some numerical solutions have been given.[14−17]Recently,the periodic soliton solution,doubly periodic solution and symmetry invariant solutions are investigated.[18−20]In this section,we shall consider the nonlocal symmetry and multi-front wave solution of the pKP equation from the Painlev´e analysis.

The solution of(1)can be truncated about the singularity manifold φ(x,y,t)as[5]

where u0and u1are functions with respect to the spacetime variables.By substituting the expansion(2)into(1)and balancing the coefficients of powers of φ−5and φ−4independently,we get

Substituting the expressions(2),(3)and(4)into(1),the field φ satisfies the following Schwarzian pKP form

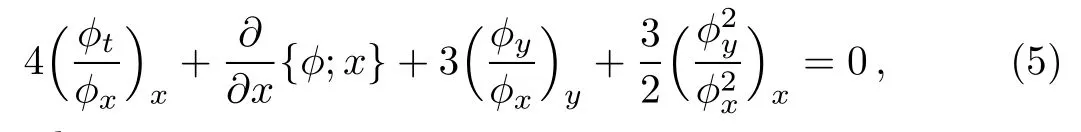
where

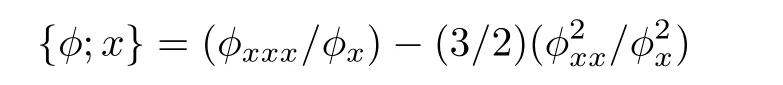
is the Schwarzian derivative.The Schwarzian form(5)is invariant under the Mbious transformation

For the special case a=d=1,b=0,c=ǫ,the symmetry of(5)reads as

By substituting the M¨obious transformation symmetry σφinto the linearized equation of(3),the nonlocal symmetry of the pKP equation(1)is

The nonlocal symmetry(8)is the residual of the singularity manifold φ.This nonlocal symmetry is thus called as the residual symmetry(RS).[10]The RS(8)can also be read out by the truncated Painlev´e expansion(2).

For the nonlocal symmetry(8),the corresponding initial value problem is

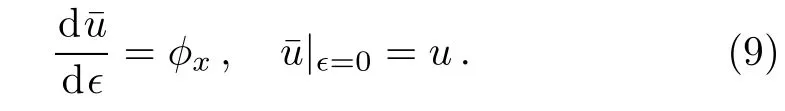
It is difficult to solve the initial value problem of the Lie’s first principle(9)due to the intrusion of the function φ and its differentiations.[10]To solve the initial value problem(9),we prolong the pKP system(1)such that RS becomes the local Lie point symmetry for the prolonged system.By localization the nonlocal symmetry(8),the potential field of φ is introduced as

The local Lie point symmetry for the prolonged systems(1),(4)and(10)reads as

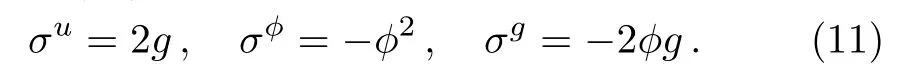
Correspondingly,the initial value problem becomes

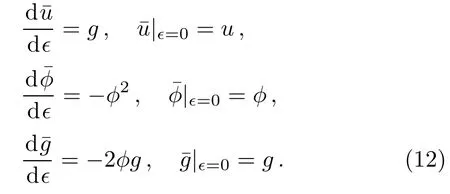
The solution of the initial value problem(12)for the enlarged pKP system(1),(4)and(10)is given as

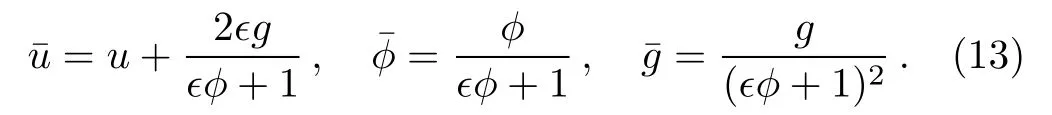
Using the finite symmetry transformations(13),one can obtain another solution from any initial solution.We take the trivial solution u=0 for(1).The multi-front waves solution for(4)and(5)is supposed as

where kn,lnand ωnare arbitrary constants.The multifront waves solution(14)is the solution of(4)and(5)only with the relations

The multiple-front waves of Eq.(1)present in the following form using(10),(13)and(14)

For the interaction behaviors of the multiple-front waves(16),we discuss the details of interactions between two front waves solution as the specific and typical.The interactions are classified into two cases,i.e.,k1k2<0 and k1k2>0.[21−22]It represents the head-on coalescence and overtaking coalescence respectively.We show the evolution of two fronts u with the parameters n=2,k1=1,l1=1,k2= −1,ǫ=1/2 in Fig.1.It illustrates two fronts along the opposite propagation direction in y-axis coalescing into one large front in their interaction region of the(x,y)-plane.As comparison,Fig.2 shows coalescence of two fronts with the same propagation direction in y-axis k1k2>0,in which the large-amplitude front with faster velocity overtakes the small-amplitude one.The parameters are n=2,k1=1,l1=1,k2=3,ǫ=1/2.It is obviously that the two front waves solution may combine into a single front wave after collision(soliton fusion).Neither elastic scattering nor fission does exist in both interaction modes.

RemarkThe multiple-front waves are established with variety of powerful methods,such as the Cole-Hopf transformation and perturbation expansion method,the multiple exp-function method and the Hirota’s bilinear method.[21−25]In this paper,we obtain the multiple-front waves with truncated Painlev´e expansion related nonlocal symmetry.

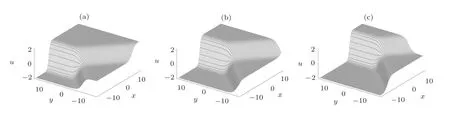
Fig.1 Plot the propagation of two front waves expressed by(16)with the parameters n=2,k1=1,l1=1,k2= −1,ǫ=1/2.(a)t=−6;(b)t=0;(c)t=6.It is obviously that two fronts propagate with the opposite direction in y-axis and coalesce into one large front in their interaction region.

Fig.2 Plot the propagation of two front waves expressed by(16)with the parameters n=2,k1=1,l1=1,k2=3,ǫ=1/2.(a)t=−1;(b)t=0;(c)t=1.It shows that two fronts propagate with the same direction in y-axis and the large-amplitude front with faster velocity overtakes the small-amplitude one.

3 CTE Solvability for pKP System

The consistent tanh expansion writes as the following form by using the leading order analysis[10]

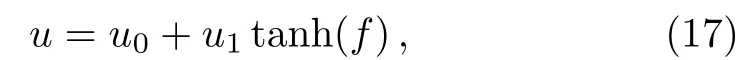
where u0,u1and f are arbitrary functions of(t,x,y).By substituting(17)into the pKP system(1)and vanishing the coefficients of powers of tanh5(f),tanh4(f)and tanh3(f),we obtain

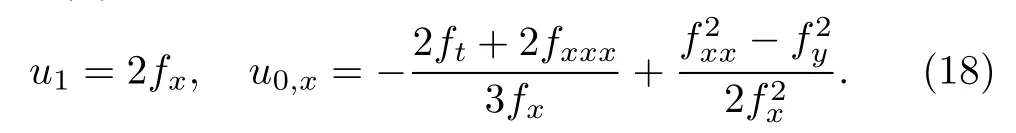
Collecting the coefficient of tanh2(f)and using(18),the consistent condition reads

The coefficients of tanh1(f)and tanh0(f)are identically zero by using(19).The consistent condition(19)can also be written as

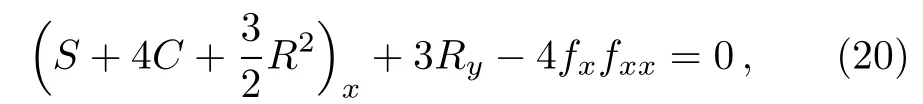
where C=ft/fx,R= φy/φx,S={φ;x}= φxxx/φx−(3/2)(φ2xx/φ2x).The pKP system for u0,u1and f is consistent,or,not over-determined,the expansion(17)is called a CTE and the pKP system(1)is CTE solvable system.[9]The nonauto-BT theorem for the pKP equation(1)is given by using the CTE approach.

Nonauto-BT TheoremIf the solution f satisfies the consistent condition(19),then u for equation(21)is also a solution of the pKP system(1)

where G(y,t)is arbitrary functions of y and t.

By means of the nonauto-BT theorem,we can obtain some special exact solutions of the pKP equation,in particularly the interaction solutions among solitons and other kinds of complicated waves.In the next section,some concrete interesting examples are given via above nonauto-BT theorem.

4 Interaction Solutions for pKP System

A quite trivial straight line solution of(19)has the form

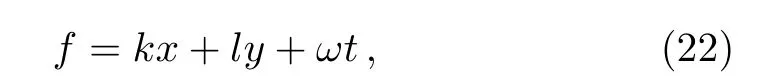
where k,l and ω are the free constants.Substituting the trivial solution(22)into(21),the exact solution of pKP system yields

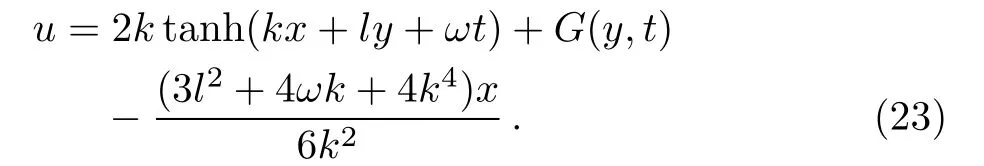
The nontrivial solution of the pKP equation is given from some quite trivial solution of(22).Actually,the solution of the pKP equation may have quite rich structures due to an arbitrariness function of(23).The parameters are k=1,l=2,ω = −2 both in Figs.3(a)and 3(b).One kink soliton coupled to the periodic wave background shows in Fig.3(a)with the arbitrary function G(y,t)=sin(y+t).Figure 3(b)plots the interaction between one kink and one soliton solution with the arbitrary function G(y,t)=1/[1+(y+t)2].It is obvious that the interaction behavior is different with selecting different parameters.

To find the other types of interaction solutions,we can look for the solutions with one straight line(22)plus an undetermined waves for the f field.The interaction solutions between solitons and multiple resonant soliton solutions of the pKP equation assume

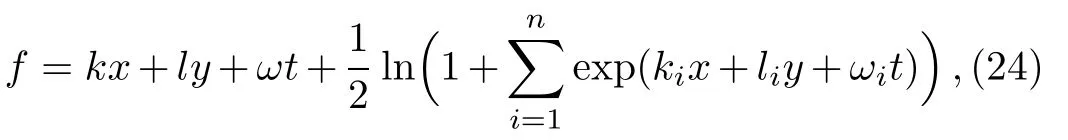
where kiare arbitrary constants while liand ωiare determined by the relations

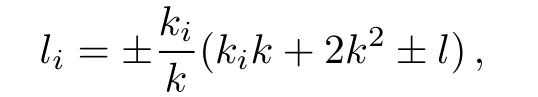
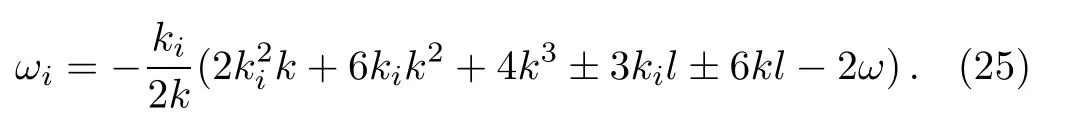
The solution of pKP equation will be obtained by substituting(24)into(21).Because the expression of u is quite complicated,we neglect write it down here and only plot their figures under the special values of the parameters.Figure 4 displays the special interaction solution with the symbol“±”in(25)as“+”and the parameters selected as n=2,k=2,l=1,ω =2,k1= −1,k2= −2.The arbitrary function G(y,t)is chosen as 1/(y+t)2and sin(y+t)2for Fig.4(a)and Fig.4(b)respectively.

For the interaction solution between solitons and cnoidal periodic waves,the interaction solution reads as

where k0,l0, ω0,k,l and ω are all the free constants.Substituting the expression(26)into(19),we obtain an equation about F1(X)as

where

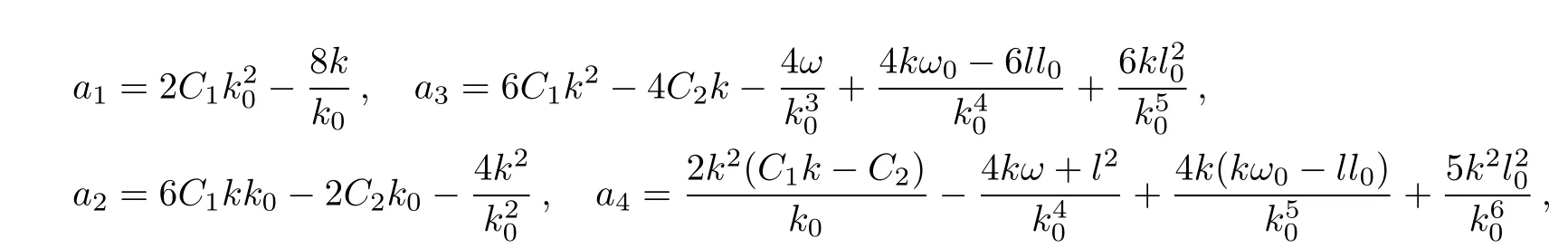
C1and C2are arbitrary constant.The solution F1in(27)can be written as[11−12]

The interaction solution between solitons and cnoidal periodic waves of(26)reads

where S is the Jacobi elliptic functionEFand Eπare the first and third incomplete elliptic integrals and r1,r2,r3,r4are related with a1,a2,a3,a4in the following relations

Fig.3 (a)Plot of one kink soliton in the periodic wave background expressed by(23)with the arbitrary function G(y,t)=sin(y+t);(b)Plot of the interaction between one kink and one soliton solution by(23)with the arbitrary function G(y,t)=1/[1+(y+t)2].The parameters are k=1,l=2,ω=−2.

In the ocean,there are some typical nonlinear waves such as interaction solutions between solitons and cnoidal periodic waves.[11]We introduce the interaction solutions may be useful for studying the ocean waves.

RemarkThe CTE method has been successfully applied to lots of nonlinear integrable[26−28]and even nonintegrable systems.[29−30]The interaction solutions between a soliton and the cnoidal waves,Painlev´e waves,Airy waves,Bessel waves are generated with the CTE method.For the pKP system,an arbitrary function is included in a nonauto-BT theorem.There exist many abundant interaction solutions of pKP equation by selecting the different arbitrary function.The interaction behaviors for pKP equation are thus different from other systems via the CTE method.

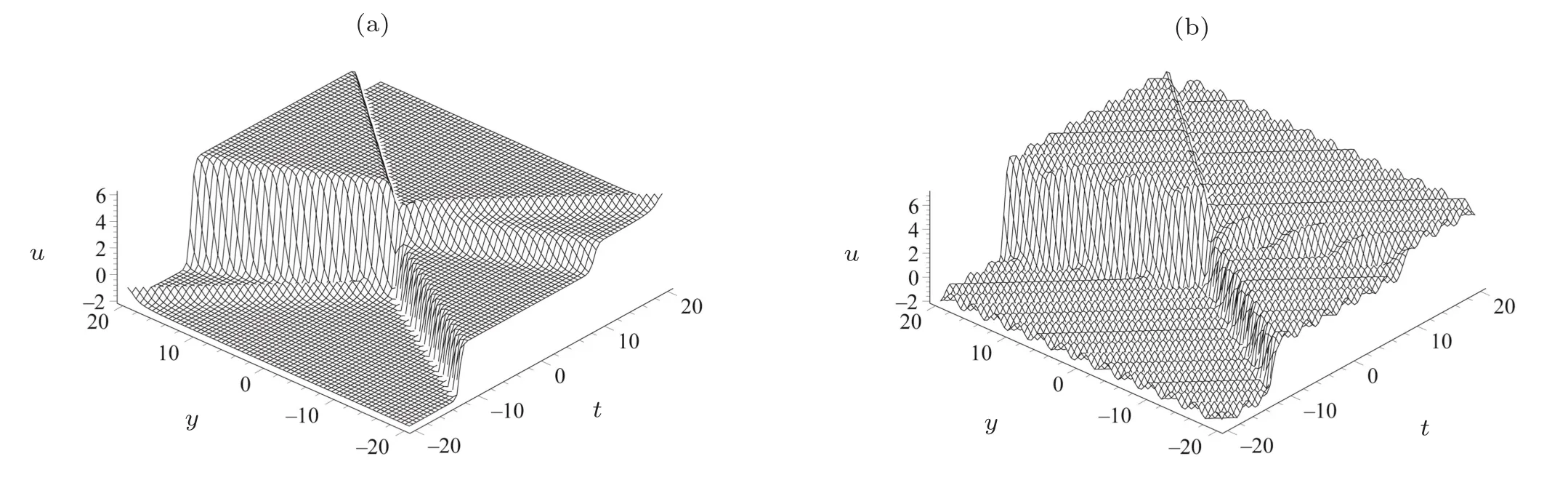
Fig.4 (a)Plot of special interaction between one soliton and two resonant soliton solutions with the arbitrary function G(y,t)=1/[1+(y+t)2];(b)Plot of the interaction between one soliton and two resonant soliton solutions in the periodic wave background with the arbitrary function G(y,t)=sin(y+t)2.The parameters are n=2,k=2,l=1,ω=2,k1=−1,k2=−2.

5 Conclusion

In summary,the nonlocal symmetry of the pKP equation is obtained with the truncated Painlev´e method.To solve the initial value problem related by the nonlocal symmetry,we prolong the pKP equation such that nonlocal symmetry becomes the local Lie point symmetry for the prolonged system.The finite symmetry transformations of the prolonged pKP system are derived by using the Lie’s first principle.The multi-front wave solution and their interaction behaviors for pKP equation are studied with the finite symmetry transformations.The inelastic interactions among the two-front wave are studied which were not reported for the pKP equation.Then,the CTE method is applied to the pKP equation.The CTE method for the pKP system leads to a nonauto-BT theorem.Abundant interaction solutions between solitons and other types of solitary waves for the pKP system are obtained with a nonauto-BT theorem.These types of interaction solutions can also be given through symmetries reduction of the prolonged systems.

In this paper,we discuss the localization procedure for one particular nonlocal symmetry,i.e.,the residual symmetries. There are many methods to obtain the nonlocal symmetry, such as the Darboux transformation,[11−12,31−32]the B¨acklund transformation,[33]and the nonlinearizations.[34−35]How to apply these various nonlocal symmetries to obtain new interaction solutions is an important topic.

References

[1]C.S.Gardner,J.M.Greene,M.D.Kruskal,and R.M.Miura,Phys.Rev.Lett.19(1967)1095.

[2]R.Hirota,The Direct Method in Soliton Theory,Cambridge University Press,Cambridge(2004).

[3]P.J.Olver,Application of Lie Group to differential Equation,Springer-Verlag,Berlin(1986);G.W.Bluman and S.C.Anco,Symmetry and Integration Methods for Differential Equations,Springer-Verlag,New York(2002).

[4]V.B.Matveev and M.A.Salle,Darboux Transformations and Solitons,Springer,Berlin(1991).

[5]J.Weiss,M.Tabor,and G.Carnevale,J.Math.Phys.24(1983)522.

[6]C.Rogers and W.K.Schief,B¨acklund and Darboux Transformations Geometry and Modern Applications in Soliton Theory,Cambridge Texts in Applied Mathematics,Cambridge University Press,Cambridge(2002).

[7]X.Y.Tang,S.Y.Lou,and Y.Zhang,Phys.Rev.E 66(2002)046601.

[8]X.L,Commun.Nonlinear Sci.Numer.Simulat.19(2014)3969;W.M.Moslem,S.Ali,P.K.Shukla,and X.Y.Tang,Phys.Plasmas 14(2007)082308.

[9]S.Y.Lou,Stud.Appl.Math.134(2015)372.

[10]X.N.Gao,S.Y.Lou,and X.Y.Tang,J.High Energy Phys.05(2013)029.

[11]X.R.Hu,S.Y.Lou,and Y.Chen,Phys.Rev.E 85(2012)056607.

[12]X.P.Cheng,S.Y.Lou,C.L.Chen,and X.Y.Tang,Phys.Rev.E 89(2014)043202.

[13]M.J.Ablowitz and P.A.Clarkson,Nonlinear Evolution Equations and Inverse Scattering Transform,Cambridge University Press,Cambridge(1990).

[14]D.Kaya and S.M.El-Sayed,Phys.Lett.A 320(2003)192.

[15]D.Li and H.Zhang,Appl.Math.Comput.146(2003)381.

[16]Z.Dai,S.Li,D.Li,and A.Zhu,Chin.Phys.Lett.24(2007)1429.

[17]Z.D.Dai,Y.Huang,et al.,Chaos,Solitons&Fractals 40(2009)946.

[18]Z.Dai,J.Liu,and Z.Liu,Commun.Nonlinear Sci.Numer.Simul.15(2010)2331.

[19]D.Q.Xian and H.L.Chen,Appl.Math.Comput.217(2010)1340.

[20]R.K.Gupta and A.Bansal,Appl.Math.Comput.219(2013)5290.

[21]S.Wang,X.Y.Tang,and S.Y.Lou,Chaos,Solitons&Fractals 21(2004)231.

[22]Z.Y.Sun,Y.T.Gao,et al.,Wave Motion 46(2009)511.

[23]A.M.Wazwaz,Appl.Math.Comput.190(2007)1198;A.M.Wazwaz,Commun.Nonlinear Sci.Numer.Simulat.17(2012)491;A.M.Wazwaz,Comput.Fluids 97(2014)164.

[24]W.X.Ma and E.Fan,Comput.Math.Appl.61(2011)950.

[25]W.X.Ma and Z.N.Zhu,Appl.Math.Comput.218(2012)11871.

[26]S.Y.Lou,X.P.Chen,and X.Y.Tang,Chin.Phys.Lett.31(2014)070201.

[27]C.L.Chen and S.Y.Lou,Chin.Phys.Lett.30(2013)110202.

[28]B.Ren,X.Z.Liu,and P.Liu,Commun.Theor.Phys.63(2015)125;B.Ren,J.R.Yang,P.Liu,and X.Z.Liu,Chinese J.Phys.53(2015)080001.

[29]B.Ren and J.Lin,Z.Naturforsch 70a(2015)539.

[30]B.Ren,J.Yu,and X.Z.Liu,Abstr.Appl.Anal.2015(2015)213847.

[31]X.P.Cheng,C.L.Chen,and S.Y.Lou,Wave Motion 51(2014)1298.

[32]J.C.Chen,X.P.Xin,and Y.Chen,J.Math.Phys.55(2014)053508.

[33]S.Y.Lou,X.R.Hu,and Y.Chen,J.Phys.A:Math.Theor.45(2012)155209.

[34]C.W.Cao and X.G.Geng,J.Phys.A:Math.Gen.23(1990)4117.

[35]Y.Cheng and Y.S.Li,Phys.Lett.A 157(1991)22.