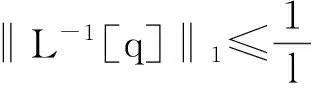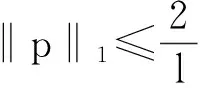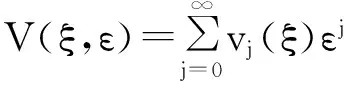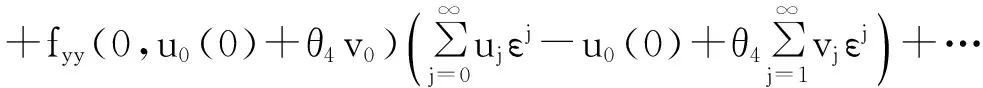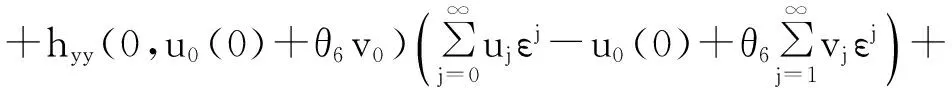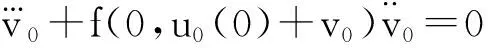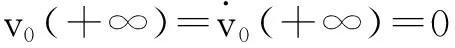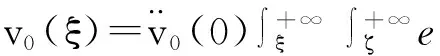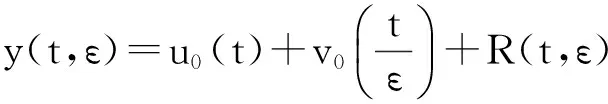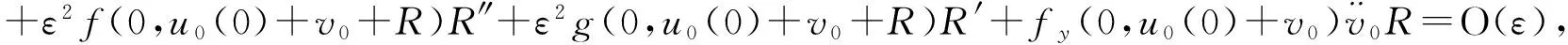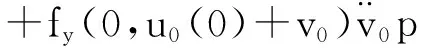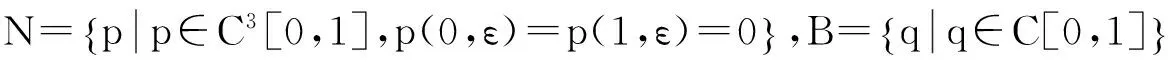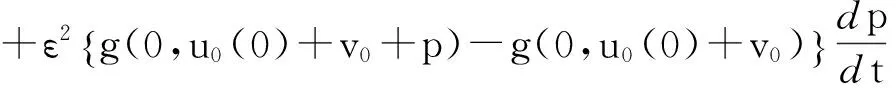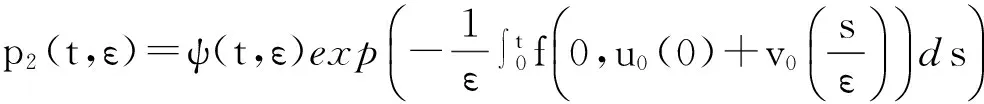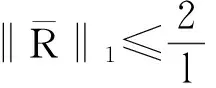一类奇摄动三阶拟线性边值问题的渐近解

许　进，　林乐义

(河海大学文天学院基础部，安徽马鞍山243031)



一类奇摄动三阶拟线性边值问题的渐近解

许进，林乐义

(河海大学文天学院基础部，安徽马鞍山243031)

[摘要]研究了一类具有边界层性质的三阶拟线性奇摄动边值问题.在适当的条件下，用合成展开法构造出该问题的形式近似式，并应用改进的不动点定理证明了解的存在性及其渐近性质.

[关键词]奇摄动； 边值问题； 边界层； 合成展开法； 不动点定理； 逆算子定理

1引言

奇摄动问题已成为学术界研究的热点问题之一. 对奇摄动问题的研究不仅在理论上具有重要的意义，而且在流体力学和量子力学等自然科学的研究中也具有广泛的应用. 近年来，对微分方程的奇摄动边值问题的研究已从二阶方程跨越到三阶方程甚至高阶方程，并已取得显著成果[1-8]. 文献[9]应用改进的不动点定理在相对较弱的条件下，研究了二阶拟线性方程奇摄动边值问题的渐近解. 本文将在文献[9]的基础上，应用改进的不动点定理进一步研究三阶拟线性方程奇摄动边值问题的渐近解.

考察如下形式的三阶拟线性Dirichlet问题：

εy‴+f(t,y)y″+g(t,y)y′+h(t,y)=0,0

(1)

y(0,ε)=A,y(1,ε)=B,y′(1,ε)=C,

(2)

其中0<ε≪1,A,B,C均为常数. 并作如下假设：

[H1] f,g,h在[0,1]×R上连续可微;

[H2] 退化问题

f(t,u)u″+g(t,u)u′+h(t,u)=0,u(1)=B,u′(1)=C

在[0,1]上有一个解u0(t)，且在[0,1]上f(t,u0(t))>0;

[H3] 存在K>0,使对介于A和u0(0)之间的任意y,都有f(0,y)≥K.

2主要引理

引理1[10](不动点定理)设(N,‖·‖1)是赋范线性空间，(B,‖·‖)是Banach空间，F是N到B的非线性映射，F[0]=0，且F可分解为

F[p]=L[p]+Ψ[p],p∈,

其中L是F在p=0的线性化算子，L和Ψ满足如下两个条件：

(i) L是双射，其逆L-1连续，即存在常数l>0使

‖Ψ[p2]-Ψ[p1]‖≤m(ρ)‖p2-p1‖1,∀p1,p2∈ΩN(ρ),

引理2[11](逆算子定理)设X和Y都是Banach空间，如果L是从X到Y上的一对一有界线性算子，则L的逆算子L-1也是有界线性算子.

3构造形式近似式

由假设[H2]可知：边界层出现在左边.

采用合成展开法[12]，先将外部解

代入(1)及y(1,ε)=B, y′(1,ε)=C,其中

f(t,U)=f(t,u0)+fy(t,u0+θ1(U-u0))(U-u0)(0<θ1<1),

g(t,U)=g(t,u0)+gy(t,u0+θ2(U-u0))(U-u0)(0<θ2<1),

h(t,U)=h(t,u0)+hy(t,u0+θ3(U-u0))(U-u0)(0<θ3<1),

并比较等式两边ε0的系数得到

f(t,u0)u″0+g(t,u0)u′0+h(t,u0)=0,u0(1)=B,u′(1)=C.

再由假设[H2]可知，它在[0,1]上有一个解u0(t).

再将U(t,ε)+V(ξ,ε)代入(1)可得

+ε2[g(ξ ε,U+V)-f(ξ ε,U)]U′+ε2[h(ξ ε,U+V)-h(ξ ε,U)]=0

或

+ε[fy(ξ ε,U+θ4V)U″+gy(ξ ε,U+θ5V)+hy(ξ ε,U+θ6V)]V=0,

(3)

式中fy(ξ ε,U+θ4V), gy(ξ ε,U+θ5V), hy(ξ ε,U+θ6V)分别写为

fy(ξ ε,U+θ4V)=fy(0,u0(0)+θ4v0)+fyt(0,u0(0)+θ4v0)ξ ε

(4)

gy(ξ ε,U+θ5V)=gy(0,u0(0)+θ5v0)+gyt(0,u0(0)+θ5v0)ξ ε

(5)

hy(ξ ε,U+θ6V)=hy(0,u0(0)+θ6v0)+hyt(0,u0(0)+θ6v0)ξ ε

(6)

将(4)-(6)代入(3)，并比较等式两边ε0的系数可得

(7)

而由U(0,ε)+V(0,ε)=A可得

v0(0)=A-u0(0),

(8)

且v0(ξ)应满足

(9)

满足(7)-(9)的解v0(ξ)可隐式地表示为

由假设[H3]可知：当ξ→+∞时, v0(ξ)是指数型小项, 即

v0(ξ)=O(exp(-Kξ))，ξ→+∞.

(10)

4解的存在性及渐近性质

应用引理来证明解的存在性，并给出解的渐近估计. 令

(11)

将(11)代入(1)-(2)可得

(12)

(13)

且由(10)可知：当ε→0时，R(1,ε)为指数型小项.

再令

其中φ(t)∈C2[0,1]且满足

于是有

现在定义N→B的映射F：

则B是一个Banach空间，而N是Banach空间的一个闭线性子空间，故也是一个Banach空间. 显然，F[0]=0，且F在p=0的线性化算子为

于是

检验引理1中的两个条件. 注意到L[p]=0的两个线性无关的解可表示为

p1(t,ε)=φ(t,ε),

其中当ε→0时，

由于当ε>0时，

故对∀q∈B,边值问题L[p]=q,p(0,ε)=p(1,ε)=0有唯一解. 因此L是双射. 又因为

=M‖p‖1,

引理1中的条件(i)成立.

任取p1,p2∈ΩN(ρ)(0<ρ<1),有

‖Ψ[p2]-Ψ[p1]‖

故存在常数c>0，使

‖Ψ[p2]-Ψ[p1]‖≤cρ‖p2-p1‖1.

即引理1中的条件(ii)也成立，其中m(ρ)=cρ. 易知

综上所述，可得到如下定理：

定理在[H1]-[H3]的假设下，对充分小的ε>0，问题(1)-(2)存在解y(t,ε)，且当ε→0时在[0,1]上一致地有

[参考文献]

[1]刘树德. 一类奇摄动半线性边值问题[J]. 数学研究，2000,33(2): 135-139.

[2]陈育森. 伴有边界摄动二阶非线性系统的奇摄动[J]. 应用数学和力学，2000,21(2): 201-208.

[3]林苏榕. 二阶非线性积分微分方程组边值问题解的渐近式[J]. 系统科学与数学，2010,30(3): 358-369.

[4]赵为礼. 一类三阶非线性边值问题的奇摄动[J]. 数学年刊，1995,16A(3): 350-358.

[5]汪志鸣，王隔霞，林武忠. 薄层流中的一类三阶奇摄动边值问题的渐近分析[J]. 应用数学学报，2006,29(4): 125-132.

[6]徐洁，陈丽华，倪明康. 一类奇摄动三阶常微分方程组的两点边值问题[J]. 华东师范大学学报：自然科学版，2008,3: 21-36.

[7]陈秀. 奇摄动高阶微分方程边值问题的套层解[J]. 大学数学，2006,22(1): 16-22.

[8]刘燕，姚静荪. 一类高阶方程的非线性边界条件的奇摄动问题[J]. 高校应用数学学报，2012,27A(2): 175-181.

[9]许进，刘树德. 利用不动点定理研究奇摄动边值问题[J]. 安徽师范大学学报：自然科学版，2012,35(2): 119-122.

[10]De Jager, E M， Jiang Furu. The Theory of Singular Perturbation[M].Amsterdam: North-Holland Publishing Co., 1996.

[11]程其襄，张奠宙，魏国强等. 实变函数与泛函分析基础(第二版)[M]. 北京：高等教育出版社, 2003.

[12]刘树德，孙建山，谢元静. 一类奇摄动拟线性边值问题的激波解[J]. 数学物理学报, 2012,32A(2): 312-319.

Asymptotic Solution of Singularly Perturbed Boundary Value Problem for the Third Order Quasilinear Equation

XUJin,LINLe-yi

(Department of Basic Course, Wentian College of Hohai University, Maanshan Anhui 243031, China)

Abstract:A class of the third-order quasilinear singularly perturbed boundary value problem with boundary layer properties is studied. Under the appropriate conditions, the formal approximation of the problem is constructed by using the method of composite expansions, and the existence and asymptotic behavior of the solution are proved by the improvement of the fixed point theorem.

Key words:singularly perturbation; boundary value problem; the boundary layer; the method of composite expansions; the fixed point theorem; the inverse operator theorem

[收稿日期]2015-11-10

[基金项目]河海大学文天学院校级自然科学课题(WT15007)

[作者简介]许进(1984-)，男，硕士研究生，助教，从事应用微分方程方向的研究.Email:privatemyye@163.com

[中图分类号]O175.14

[文献标识码]A

[文章编号]1672-1454(2016)02-0012-05