一种考虑温度影响的高效几何非线性梁-柱单元

李国强, 王　震



一种考虑温度影响的高效几何非线性梁-柱单元

李国强1,2, 王震1,3

(1. 同济大学 土木工程学院, 上海 200092; 2. 同济大学 土木工程防灾国家重点实验室, 上海 200092;3. 中国二十冶集团上海十三冶建设有限公司, 上海 201999)

摘要：在梁-柱单元位移函数中引入了轴力的影响，将传统3次位移函数改进为4次位移函数，并推导得到了考虑温度影响的几何非线性梁-柱单元.该单元的几何非线性刚度矩阵中完整考虑了单元位形变化对平衡方程的影响、温度变化对材性和单元应变的影响以及单元位形变化对几何方程的影响，进而可以考虑二阶效应、弓形效应.采用该单元编制了有限元程序，算例分析表明，该梁-柱单元精度得到了显著改善，可以极大减少非线性有限元模型的单元数量，在分析火灾下梁的悬链线效应、火灾下杆系结构连续性倒塌等问题上具有显著优势.

关键词：梁-柱单元; 几何非线性; 单元刚度矩阵; 弓形效应; 温度

近些年，随着有限元理论的发展及相关数值软件的推广，工程师可以借助计算机实现快速解决涉及温度、材料非线性、几何非线性的复杂工程结构问题.然而，为得到足够精确的数值解，往往需要将构件划分为大量的单元，对于工程结构极限状态分析，如火灾下梁的悬链线效应、火灾下连续性倒塌等问题尤其如此.单元数量的增加不仅极大增加计算代价，还极易产生数值计算的不收敛.

对几何非线性梁-柱单元，其几何非线性主要包括两方面：①空间位形变化对平衡方程的影响，对梁-柱单元而言即二阶效应；②空间位形变化对几何方程的影响，对梁-柱单元而言，即侧向变形对轴力的影响及该轴力变化对弯矩的影响，亦即弓形效应.现有有限元方程均基于假定的位移函数建立，若位移函数选取适当，并完整考虑这两者，则单元精度可得到显著改善，进而实现1个单元模拟1个构件的目标.

温度变化对梁-柱单元的影响体现在2个方面：①温度对材料性能的影响，如弹性模量折减、强度折减等，可通过材料折减系数考虑；②因温度变化而使梁、柱产生长度变化，对应的应变状态为正应变的改变，而剪应变不变，当梁、柱在伸长方向存在多余约束时，将产生温度内力.

因此，本文通过构造考虑轴力对梁-柱单元侧向变形影响的位移函数，考虑二阶效应和弓形效应的几何非线性，并进一步引入温度，推导一种考虑温度影响的高效几何非线性梁-柱单元.

1现有梁-柱单元的局限

温度变化对梁-柱单元的影响可通过材料性能折减系数、温度应变予以考虑.

1.1梁-柱理论法

在梁-柱理论中[1]，通过直接求解梁-柱单元的平衡微分方程得到精确的节点力、节点位移关系进而得到无刚体位移的非线性梁-柱单元切线刚度矩阵，其中，梁-柱单元的二阶效应由稳定函数表示.由于该稳定函数中没有考虑弓形效应(包括梁-柱侧向变形对轴向伸长的影响及该轴向变形引起的弯曲影响)[2]，因此Oran[3]改进并推导得到了考虑弓形效应的梁-柱单元.

经典的梁-柱理论方法基于能够直接求解的平衡微分方程，当考虑扭转、剪切等变形时，直接求解十分困难，因此该经典理论应用于复杂受力状态时较为困难.

此外，梁-柱理论法考虑弓形效应也是十分困难的，因此多数情况下会忽略弓形效应的影响[4].这种近似在常见的几何非线性问题中不会引起显著误差，但是在诸如梁的悬链线效应的倒塌分析中，忽略弓形效应将无法计算梁中轴力，进而出现错误的倒塌分析结果.

1.2有限单元法

现有有限元理论[5]中通常以位移元作为基本未知量，即首先假定单元的变形曲线，基于此变形曲线建立单元的有限元平衡方程.由此可以看出，位移函数的选取对于计算结果的精度起决定性作用，如果选取的位移函数与真实位移函数相差较大，需要划分较多的单元以减小误差.

对于梁单元[5]，通常假定挠度位移函数为结点位移的三次Hermite插值函数，相邻单元结点处的位移、转角均保持连续；轴向变形为结点的一次Lagrange插值函数，仅相邻单元结点处的位移保持连续.

不难看出，Hermite位移函数是弹性状态下不考虑轴力和剪切变形而仅受结点弯矩的梁精确挠曲变形函数[6].因此，基于此位移函数推导得到的梁单元，用1个单元即可精确模拟不考虑剪切而仅受结点荷载的简支梁小变形分析.但是，当问题涉及几何非线性、材料非线性、节间荷载时，梁挠曲线不再是Hermite插值函数，故需要将梁划分为多个单元，以得到近似于精确解的数值解.

在考虑几何非线性的梁单元刚度矩阵推导过程中，通常对由虚位移原理建立起来的平衡方程进行线性化处理，略去了非线性项，文献[7]通过考虑部分非线性项，即侧向变形产生的轴向伸长项，发现单元的精度得到了极大改善，用较少单元甚至1个单元就可以较为准确地模拟1个构件的力学行为.

有限元理论可以实现对梁-柱单元几何方程中高阶项的完整考虑，因此改进单元位移函数成为提高单元精度的有效方法.研究人员尝试提高位移阶次并在单元内增加内结点[8]，虽然单元精度得到了改进，但其计算过程复杂，且精度提高有限.

因此，Chan等[9]提出五次非线性梁-柱单元，该单元位移函数考虑轴力的影响，单元精度得到显著改进，计算也十分简便.经典算例表明，该单元可以实现1个或2个单元模拟1个构件.但其推导过程仅考虑单元侧向变形对轴力的影响，未能考虑该轴力变化对弯矩的影响，因此弓形效应考虑不完整.

基于此，本文提出了考虑轴力影响的四次位移函数，并推导了能完整考虑弓形效应的新梁-柱单元.由于弓形效应考虑完整，因此在处理钢梁悬链线效应等极限分析时具有显著优势.

2现有梁-柱单元对温度的考虑

在既有单元基础上，通过考虑温度对材料性能的影响、温度应变可以建立考虑温度影响的梁-柱单元.

温度对材料的物理、力学性能具有显著的影响，主要包括：①温度对材料物理性能的影响，主要包括热膨胀系数、热传导系数、比热容、密度等，用于计算结构、构件内的温度场；②温度对力学性能的影响，如强度、弹性模量、松弛、徐变等，用于计算结构、构件的内力和变形等.根据分析对象的不同，选择采用考虑温度影响的相应材料性能，进而在现有常温梁-柱单元基础上考虑温度的影响.

当单元温度发生变化时，除了材性发生变化，还会产生温度变形.如单元各部分的温度变形不受约束，则该温度变形部分不会引起应力.但如果单元受到约束或温度变化不均匀时，单元内温度变形不能自由进行，则会在单元内产生温度内力.通常，在现有常温梁-柱单元中通过附加等效温度节点荷载来考虑温度内力的影响.

3考虑温度影响的新型梁-柱单元有限元平衡方程

3.1分析模型与假定

选取平面梁-柱单元为分析对象，其节点力向量P=[NiQiMiNjQjMj]T，节点位移向量a=[uiviθiujvjθj]T，即如图1所示.式中，N为节点轴力；Q为节点剪力；M为节点弯矩；u为轴向位移；v为侧向位移；θ为转角；下标i，j为节点编号.

假定梁-柱单元内的温度沿长度方向保持不变，但在截面内可按线性变化.假定：①梁-柱单元为等截面直杆；②不考虑剪切变形；③大位移、小应变；④作用荷载为保守力，且仅作用在节点处.

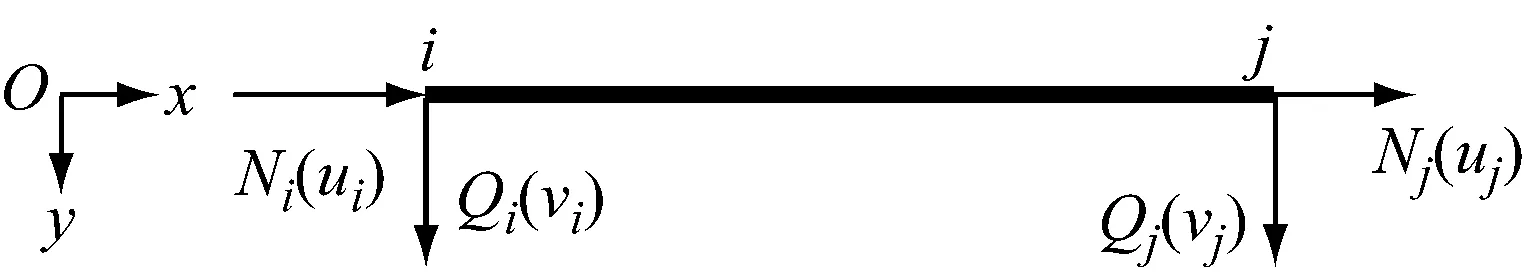
图1　梁-柱单元节点力和节点位移

3.2考虑温度影响的位移函数

初始及当前梁-柱单元位形变化如图2所示，其中Oxy为单元坐标系；O′XY为结构坐标系；α为x与X的夹角.常温下传统梁-柱单元采用三次插值函数描述其侧向变形，无法考虑轴力对其侧向变形的影响，因此本文采用四次插值函数式(1)，在传统位移边界条件式(2)基础上，通过附加平衡关系式(3)考虑轴力对侧向变形的影响，由广义坐标法即可得到侧向变形四次位移函数.新单元轴向变形仍采用Lagrange一次插值函数.新得到的全量和增量位移函数见式(4).

(1)

(2)

式中：a0～a4为待定系数；ξ为自然坐标，ξ=x/l，l为单元长度.

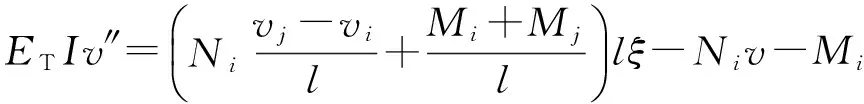
(3)

式中：ET为考虑温度影响的弹性模量；I为截面惯性矩.a(da)=

(4)

(5)

当考虑温度影响时，通常仍假定考虑温度影响的单元位移函数与常温下形式一致，仍为结点位移的四次函数.

图2　力学模型

从式(4)可以看出，当ρ=0时，新位移函数与Hermite三次位移函数一致.参数ρ考虑了轴力对单元侧向变形的影响.

3.3考虑温度影响的几何方程

考虑温度的梁-柱单元的应变ε由两部分组成:①受力产生的变形，即机械应变εM；②截面温度变化产生的变形，即温度应变εT.即ε=εM+εT.

假定截面温度T线性变化，并进一步分解为轴向均匀温度和轴向非均匀温度，即式(6)；截面应变εT分解为轴向均匀应变和轴向非均匀应变，即式(7).

(6)

(7)

式中：k为截面上边缘点与下边缘点的温度比值；ΔTb为截面下边缘点的温度变化；η为截面高度自然坐标，η=y/h，h为单元截面高度；αs为钢材温度线膨胀系数.

3.4考虑温度影响的材料本构关系

本文推导的考虑温度影响的梁-柱单元主要用于杆系结构弹性力学分析，因此温度对材料性能的影响主要体现在温度对弹性模量的影响.

考虑温度影响的材料本构关系见式(8).

(8)

式中：σ为材料应力；ε为材料应变.

3.5考虑温度影响的有限元平衡方程

基于新推导得到的位移函数可以建立考虑温度影响的梁-柱单元虚功方程式(9).结合本构关系，则可得到梁-柱单元全量平衡方程(10)、增量平衡方程式(11).

∫δεTσMdV-∫δuTfdV-∫δuTtdS=0

(9)

(10)

dP+dPT

(11)

式中：δε为虚应变；σM为机械应力；V为单元体积；δu为虚位移；f为作用于单元的体积力；t为作用于单元的边界分布力；S为单元面积；B为应变矩阵；DT为考虑温度的本构关系矩阵；P为常温下等效节点荷载；PT为高温下等效节点荷载；下标L表示线性，N表示非线性，s表示割线，t表示切线.

需要指出的是，常温下的传统有限元理论中通常忽略几何方程中的高阶项，而此项恰恰反映了弓形效应，即梁-柱单元侧向变形对轴力的影响及该轴力变化对弯矩的影响.忽略高阶项的影响后，本节所得有限元平衡方程与传统有限元平衡方程及梁-柱理论法得到的平衡方程形式一致.

因此，为提高单元精度，本文在推导考虑温度影响的有限元平衡方程过程中考虑了几何方程高阶项的影响.

4考虑温度影响的割线刚度矩阵

4.1线性刚度矩阵

由全量有限元平衡方程可以得到线性割线刚度矩阵表达式(12)，该项反映了小变形条件下节点力与节点位移的关系.

(12)当ρ=0时，该项即与传统Hermite单元线性刚度矩阵一致.

(13)

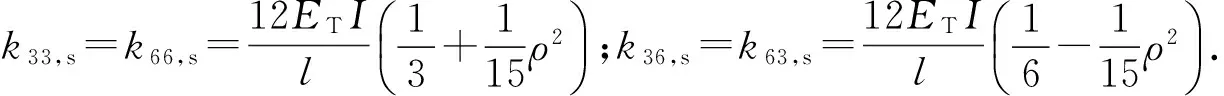
4.2大位移刚度矩阵

经典梁-柱理论法通常难以考虑弓形效应的影响，而经典有限元理论亦通常忽略单元位移函数中高阶项的影响.此高阶项考虑了侧向变形对轴力的影响及该轴力变化对弯矩的影响，即弓形效应，这种效应在单元大位移条件下并不能忽略.

考虑单元位移函数中的高阶项得到的大位移刚度矩阵式如(14)，该式由三部分组成，分别表示侧向变形对轴力的影响(式(15))以及该轴力变化对剪力、弯矩的影响(式(16)和(17)).Chan等[9]提出的单元仅考虑了式(15)的影响，推导过程中未能考虑式(16)和(17)的影响.

kD,s=kD1,s+kD2,s+kD3,s

(14)

(15)

(16)

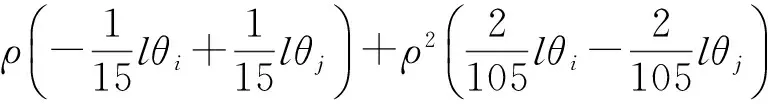
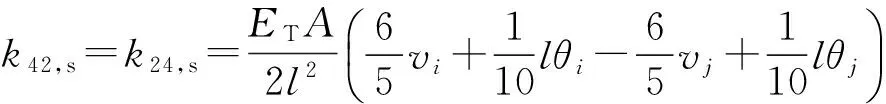
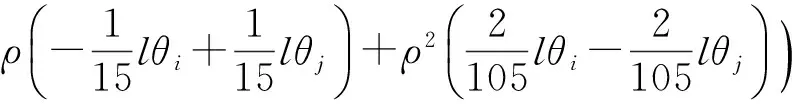
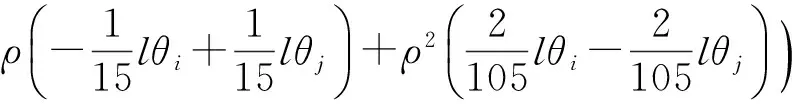
(17)

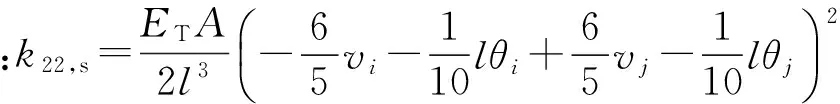
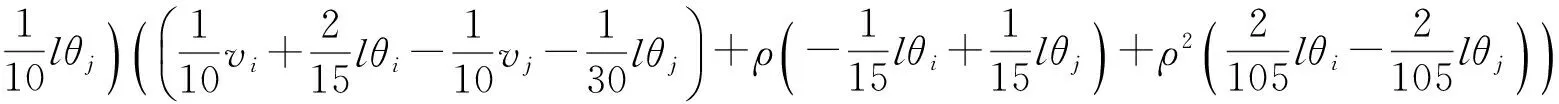
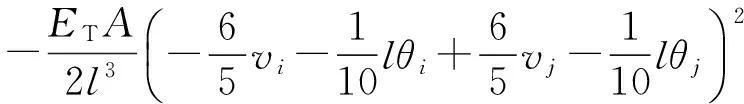
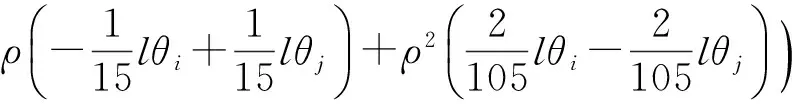
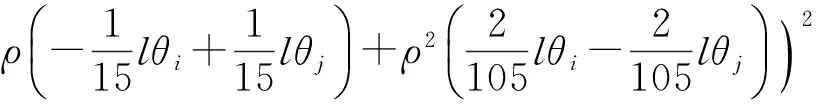
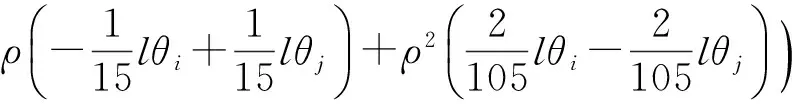
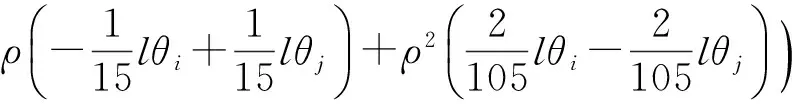
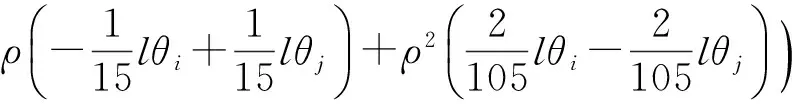
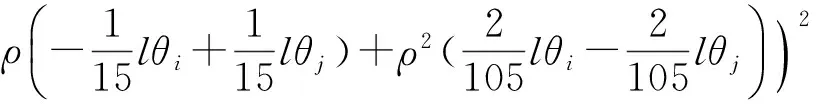
5考虑温度影响的切线刚度矩阵

5.1线性刚度矩阵

同理可以得到线性切线刚度矩阵式(18).

(18)

5.2几何刚度矩阵

由增量有限元平衡方程可以得到几何切线刚度矩阵式(19)，该项考虑了单元内力对单元变形的影响，即“二阶效应”.

(19)

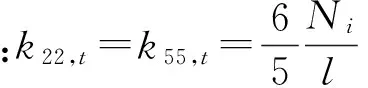
5.3大位移刚度矩阵

同样，如考虑高阶项的影响，可以得到大位移切线刚度矩阵式(20)，通过该项的引入可以考虑单元侧向变形引起的轴力变化；如忽略此项，则无法计算极限分析中钢梁的悬链线效应，即无法计算由于侧向变形产生的轴力.

(20)

6等效温度节点荷载

同样，可以推导得到等效温度节点荷载式(21)，即温度变化引起的载荷项.

(21)

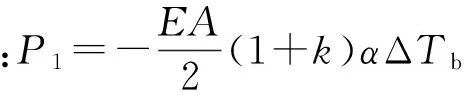
7算例分析

利用本文方法(新单元)编制了非线性有限元程序，采用弧长法确定常温下的增量步长[10]，采用线性升温速度确定高温下的增量步长，每一增量步内采用Modified Newton-Raphson方法迭代求解.通过本程序与通用商业有限元软件ABAQUS计算结果的对比分析来验证新单元的精度和效率.

采用ABAQUS提供的B23单元进行模拟，B23单元为欧拉-伯努利单元[11]，其侧向位移采用Hermite三次插值函数，轴向位移采用Lagrange一次插值函数.该单元不能考虑剪切变形，但可以考虑剪力对平衡方程的影响.

为简化计算，2个算例中第1个升温步均设定为常温，并施加预定荷载.在后续升温步中线性升温至设定温度，同时保持荷载不变，各升温步设定温度见表1.各个温度下钢材弹性模量折减系数采用规范EC3的建议值[12]，见表2.

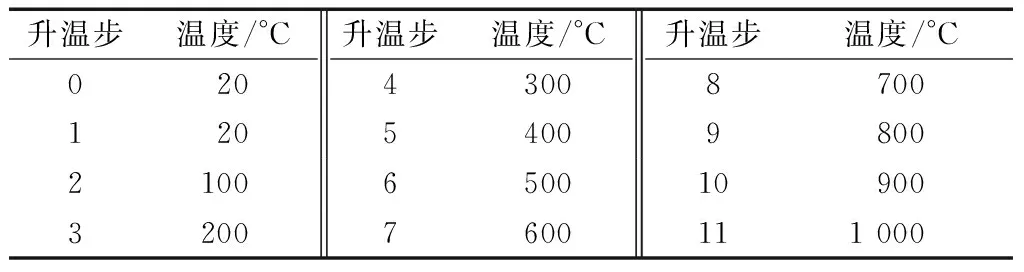
表1　升温步的设计

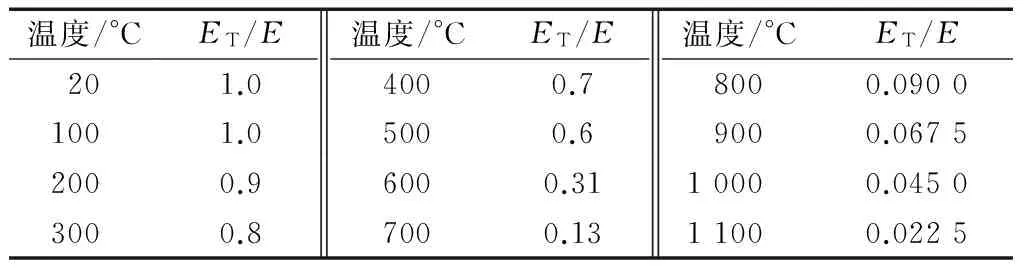
表2　高温下钢材弹性模量折减系数

7.1两端固定梁

以两端固定梁为分析对象，如图3，图中梁截面面积A为1.8×105mm2，截面惯性矩I为5.4×109mm4，梁长度L为6 000 mm，跨中集中荷载P为5×108N.首先常温下在跨中施加集中荷载，之后对梁进行恒载升温，升温速度见表1.本算例可以考察梁内轴力产生过程及轴力对挠度的影响，即火灾下钢梁的悬链线效应.

图3　两端固定梁

由图4、图5可以看出：1个、2个新单元与20个B23单元计算得到的荷载-挠度关系稍有偏差，但轴力-挠度、挠度-升温步、轴力-升温步关系基本一致.说明本文方法得到的梁-柱单元可以准确描述高温下两端固定梁内的悬链线效应，精确计算出升温过程中由于悬链线效应产生的轴力.

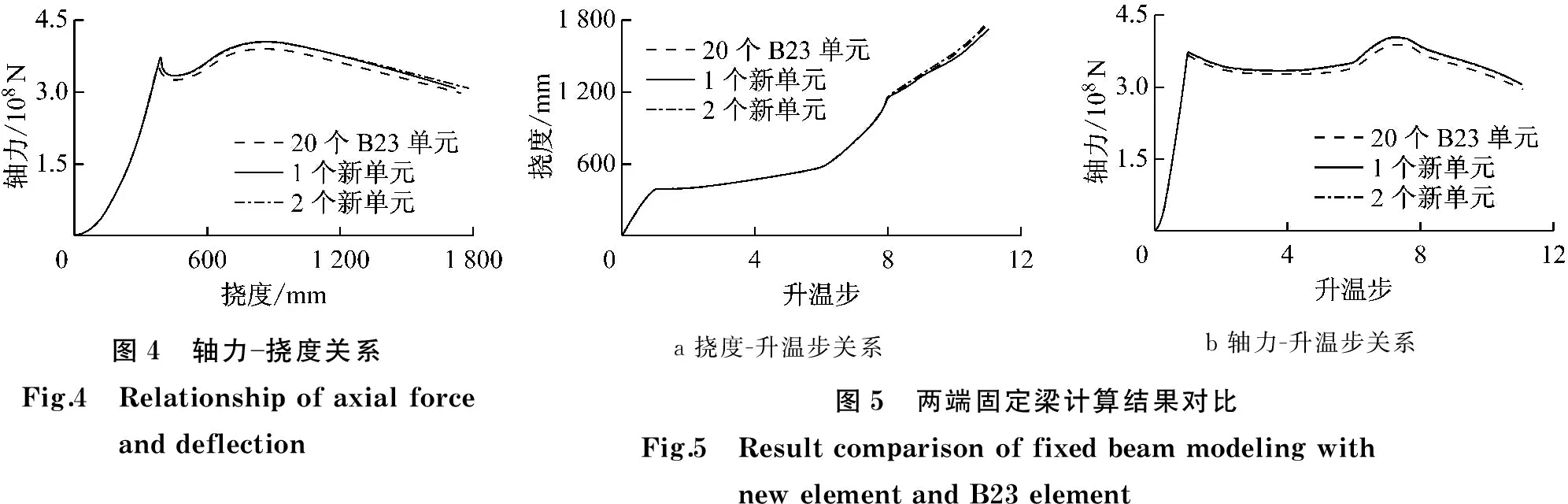
图4 轴力挠度关系Fig.4 Relationshipofaxialforceanddeflectiona挠度-升温步关系b轴力-升温步关系图5 两端固定梁计算结果对比 Fig.5 ResultcomparisonoffixedbeammodelingwithnewelementandB23element

7.2Г形钢架

以Г形钢架为研究对象，如图6，图中梁截面面积A为6.25×104mm2，截面惯性矩I为3.25×108mm4，梁长度L为3 000 mm，角点集中荷载P为4×106N，荷载作用点距角点偏心距e为30 mm.首先在角点施加竖向集中荷载和弯矩，之后保持荷载不变，对Г形钢架线性升温，升温步设计见表1.本算例考察钢架内的悬链线效应及该效应对转角的影响.

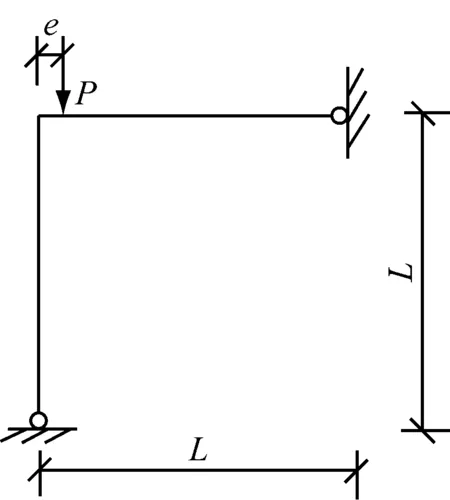
图6　Г形钢架

由图7、图8可以看出：本文提出的1个、2个新单元计算结果与20个B23单元计算结果基本一致，可以准确反映柱的失稳及高温下梁内悬链线效应，具有较高的计算效率和精度.

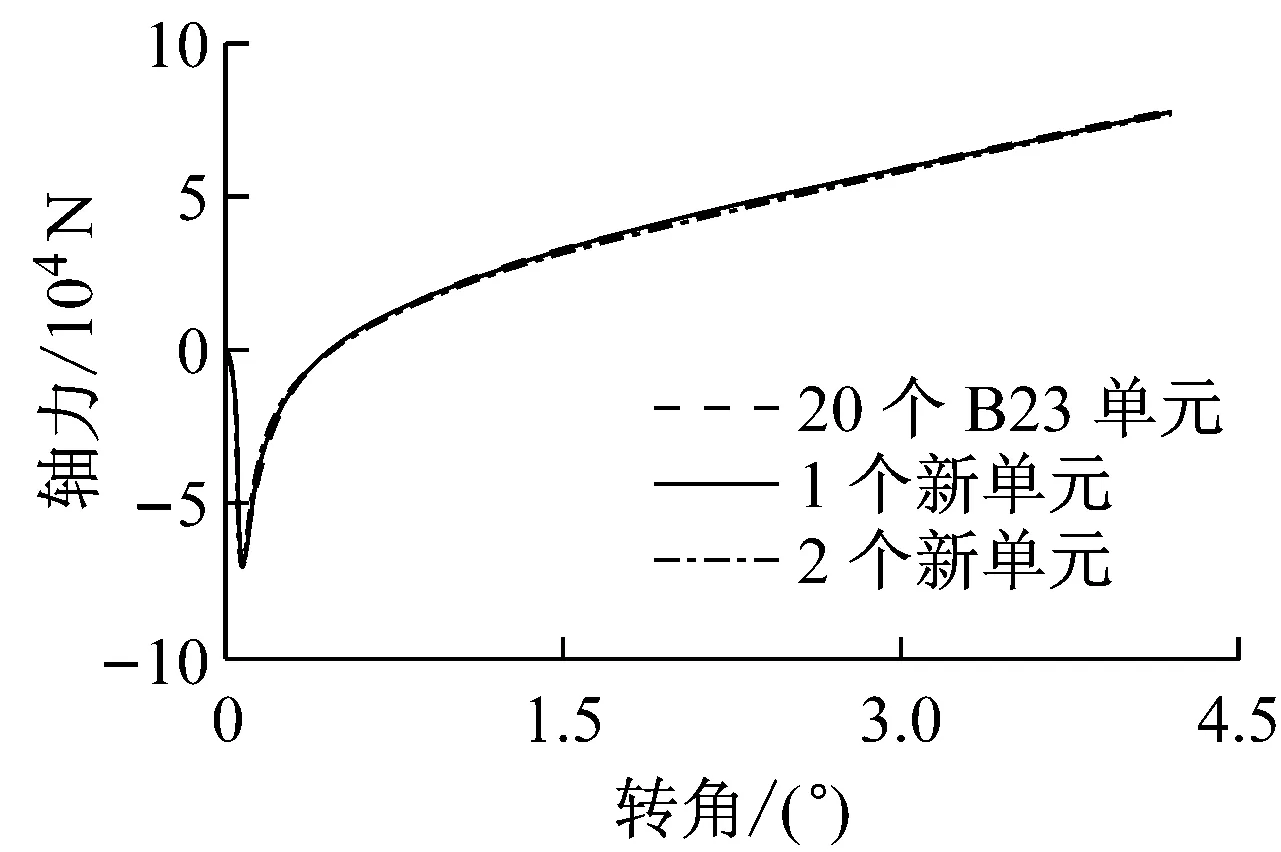
图7　轴力-转角关系

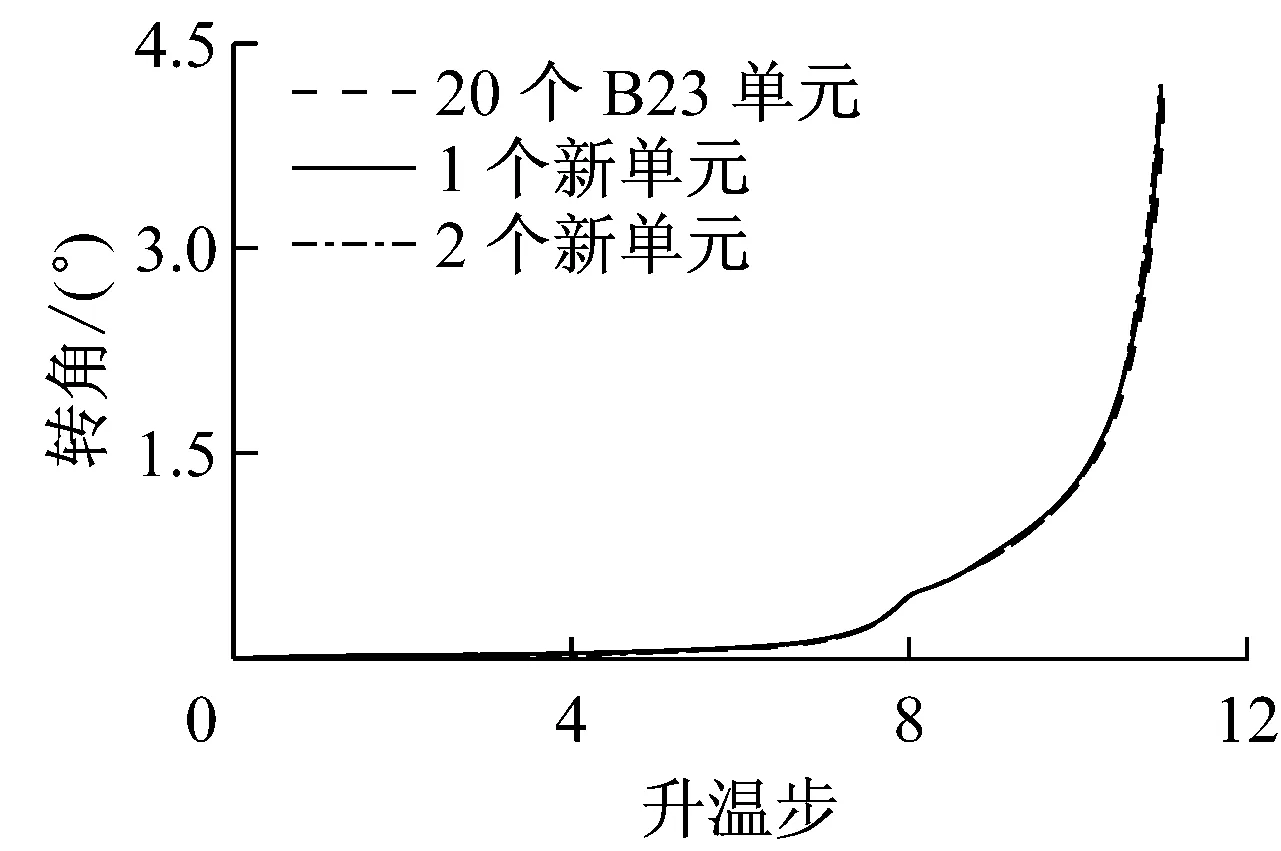
a 转角-升温步关系

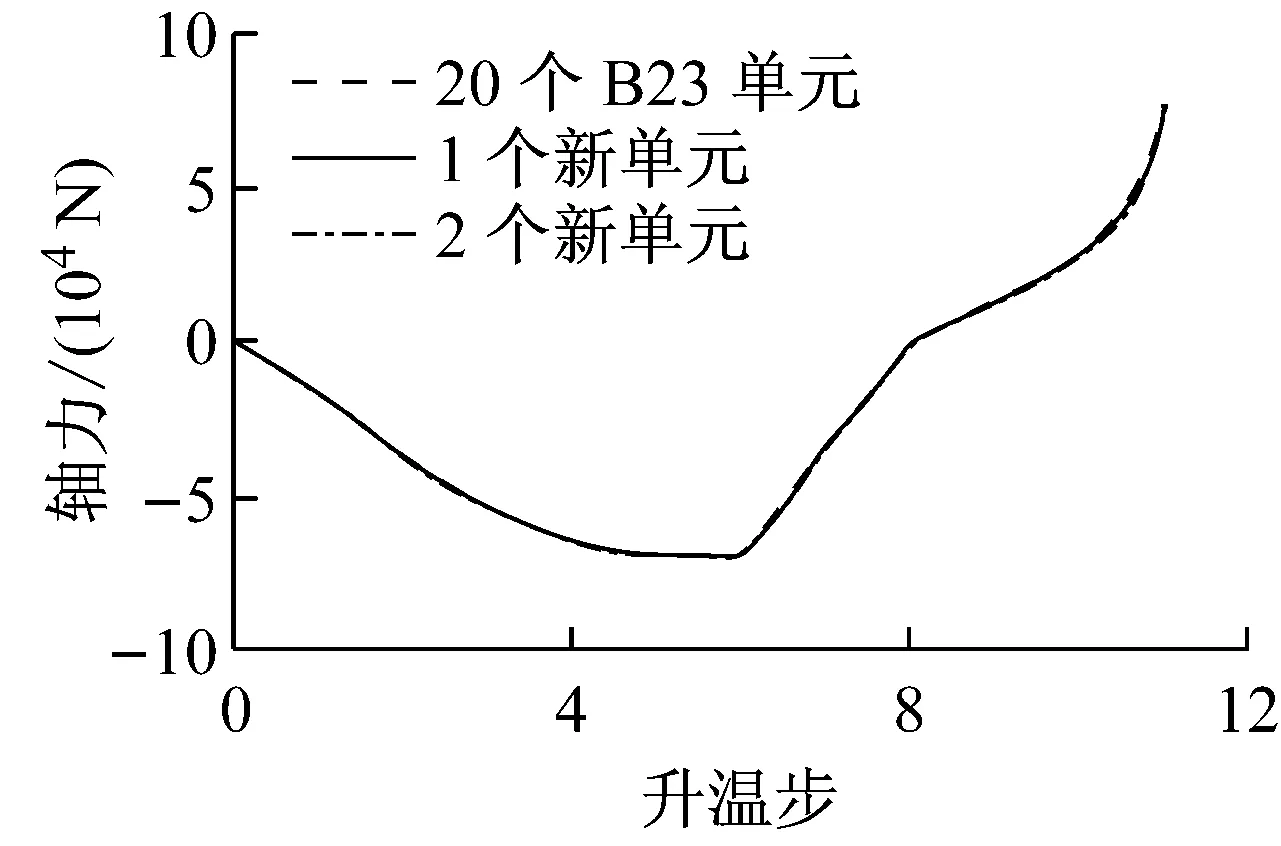
b 轴力-升温步关系

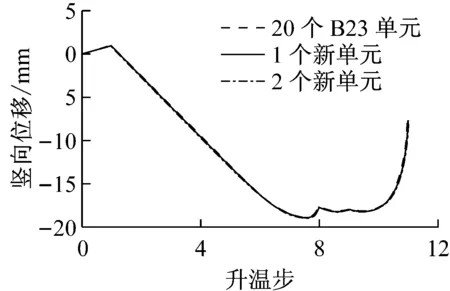
c 竖向位移-升温步关系

8结语

传统梁柱理论难以考虑侧向变形对轴力的影响及该轴力变化对弯矩的影响，传统有限元理论通常忽略几何方程高阶项的弓形效应影响.虽有相关文献考虑高阶项，但由于其位移函数采用三次插值函数，所以无法考虑轴力对单元位移函数的影响，需将构件划分为多个单元以实现极限分析，如火灾下钢梁悬链线效应、火灾下倒塌分析等.本文依据现有理论建立了考虑温度和轴力影响的高效梁-柱单元，并通过完整考虑几何非线性的影响实现了1个单元模拟1个构件的目的.

与软件ABAQUS中B23单元的经典算例对比分析表明：本文提出的梁-柱单元具有较高的精度，可实现火灾下极限分析时用1个单元模拟1个构件，为火灾下杆系结构梁悬链线效应、非线性连续性倒塌等火灾极限状态的数值分析提供高效梁-柱单元.

本文虽以平面梁-柱单元为分析对象，但其理论也可推广至空间梁-柱单元.但本梁-柱单元由目前研究知仅适用于弹性材料阶段，暂未拓展到塑性阶段，是否适用于塑性阶段，需进一步深入研究.

参考文献:

[1]李国强, 刘玉姝, 赵欣. 钢结构框架体系高等分析与系统可靠度设计[M]. 北京: 中国建筑工业出版社, 2006.

LI Guoqiang, LIU Yushu, ZHAO Xin. Advanced analysis and reliability design of steel frame system [M]. Beijing: China Architecture & Building Press, 2006.

[2]刘坚. 钢结构高等分析的二阶非弹性理论与应用[M]. 北京: 科学出版社, 2012.

LIU Jian. Second order inelastic theory and application for advanced analysis of steel structures [M]. Beijing: Science Press, 2012.

[3]Oran C. Tangent stiffness in space frames [J]. Journal of the Structural Division, ASCE, 1973, 99(6): 987.

[4]Goto Y, Chen W F. On the computer-based design analysis for the flexibly jointed frames [J]. Journal of Constructional Steel Research, 1987(8): 203.

[5]王勖成. 有限单元法[M]. 北京: 清华大学出版社, 2003.

WANG Xucheng. Finite element method [M]. Beijing: Tsinghua University Press, 2003.

[6]Chan S L, Zhou Z H. Second-order elastic analysis of frames using single imperfect element per member [J]. Journal of Structural Engineering, 1995, 121(6): 939.

[7]Al-Bermani F G A, Kitipornchai S. Nonlinear analysis of thin-walled structures using least element/member [J]. Journal of Structural Engineering, 1990, 116 (1): 215.

[8]So A K W, Chan S L. Buckling analysis of frames using 1 element/member [J]. Journal of Constructional Steel Research, 1991, 20(4): 271.

[9]Chan S L, Zhou Z H. Pointwise equilibrating polynomial element for nonlinear analysis of frames [J]. Journal of Structural Engineering, 1994, 120(6): 1703.

[10]Crisfield M A. A fast incremental/iterative solution procedure that handles ‘snap-through’ [J]. Computers & Structures, 1981, 13(1/3): 55.

[11]Dassault Systèmes Simulia Corp. ABAQUS 6.11 theory manual [M]. [S.l.]: Dassault Systemes Simulia Corp, 2011.

[12]李国强,韩林海,楼国彪，等. 钢-混凝土组合结构抗火设计[M]. 北京: 中国建筑工业出版社, 2006.

LI Guoqiang, HAN Linhai, LOU Guobiao,etal. Fire resist design of steel structures and steel-concrete composite structures [M]. Beijing: China Architecture & Building Press, 2006.

收稿日期：2015-08-08

基金项目：国家自然科学基金(51120185001)

通讯作者：王震(1986—)，男，博士生，主要研究方向为钢结构高等分析、钢结构抗火等.E-mail: 2011zwang@tongji.edu.cn

中图分类号：TU311

文献标志码：A

An Efficient Geometric Nonlinear Beam-Column Element Considering Temperature

LI Guoqiang1,2, WANG Zhen1,3

(1. College of Civil Engineering, Tongji University, Shanghai 200092，China; 2. State Key Laboratory for Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China; 3. MCC20 Shanghai Shisanye Construction Co. Ltd., Shanghai 201999, China)

Abstract：Instead of traditional cubic Hermitian interpolation function, axial force is considered in element deformation in this paper, and a fourth order interpolation function is employed to form a new beam-column element considering thermal effect. Influence of element deformation on equilibrium equation and geometric equation, and influence of temperature on material properties and strain formulation are considered in new element, known as second-order effect and bowing effect. A finite element program was written to verify the efficiency and accuracy of the new element against B23 in ABAQUS. It is concluded that the element number can be greatly reduced under the same accurate condition, and be superior in dealing with limit analysis, such as catenary effect of beam in fire and nonlinear progressive collapse analysis in fire.

Key words：beam-column element; geometric nonlinearity; element stiffness matrix; bowing effect; temperature

第一作者： 李国强(1963—)，男，教授，博士生导师，工学博士，主要研究方向为多高层钢结构、钢结构抗震、钢结构抗火、钢结构抗爆.

E-mail: gqli@tongji.edu.cn