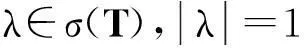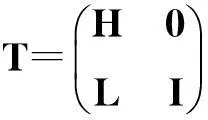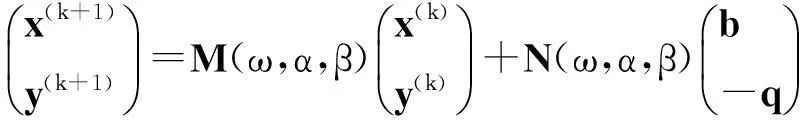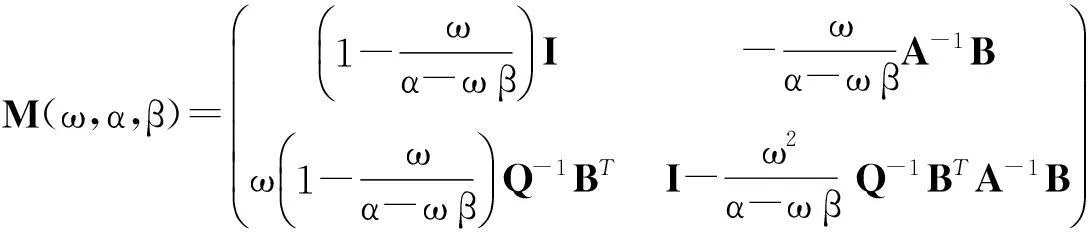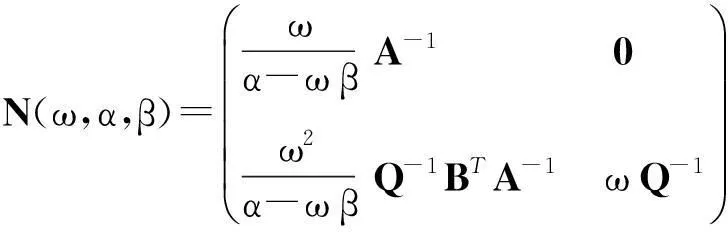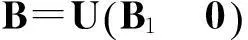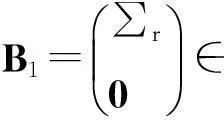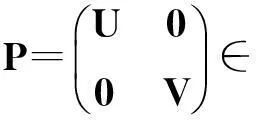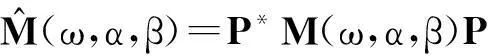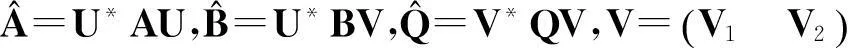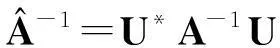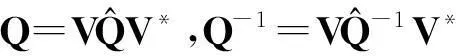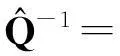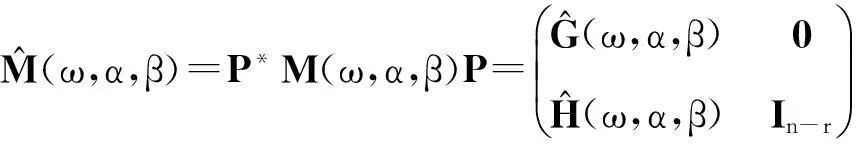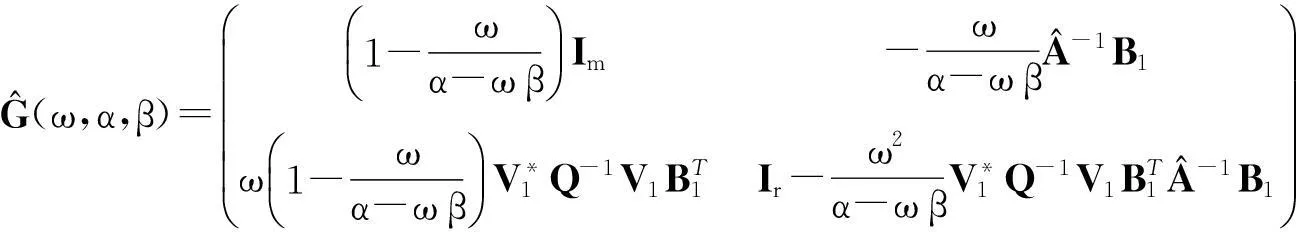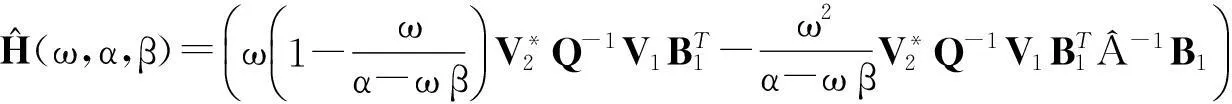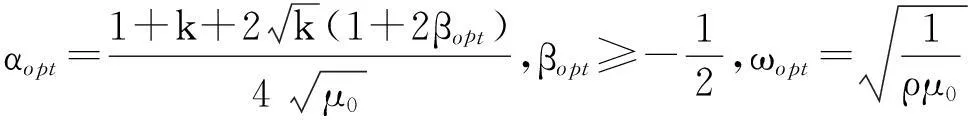奇异鞍点问题的一类迭代算法的半收敛性

周小燕

(浙江科技学院 理学院，杭州 310023)



奇异鞍点问题的一类迭代算法的半收敛性

周小燕

(浙江科技学院 理学院，杭州 310023)

摘要:提出了奇异鞍点问题的一类基于对矩阵的一种带2个实参数α和β的新的分裂的广义的SOR-like方法，得到了此方法半收敛的条件，以及最优参数与相应的最优半收敛因子。

关键词:鞍点问题；GSOR-like方法；半收敛；最优参数

考虑具有以下形式的鞍点问题：

(1)

式(1)中,A∈m×m为对称正定(SPD)矩阵;B∈m×n(这里假定m≥n)；BT是B的转置矩阵；向量x,b∈m,y,q∈n,b,q是已知向量。

鞍点问题来自于非线性约束最优化(连续2次规划问题和内点法)、流体动力学(Stokes方程)、不可压缩弹性分析、电路分析及结构分析等。鞍点问题的求解与一般的线性方程组求解一样，有直接法和迭代法2种。直接法只进行有限步计算,所以，在不计入舍入误差的情况下,可以在有限步求得方程组的精确解,它比较适合阶数较低的线性方程组。迭代法是从解的一个初始估计值开始,逐步对它进行改进,直到达到所需的精度,理论上说,须经过无限次迭代才能收敛到真解；但实际上,只要用某种度量方式(如残量的范数)，当度量的误差已小于某个给定值时,迭代即可终止。当系数矩阵是稀疏矩阵,且方程的阶数较大时,迭代法就比较适合,因为它运算量小,内存需求小。

当rank(B)=n，即B是列满秩矩阵，鞍点问题(1)(式(1))有唯一解。许多研究者对鞍点问题(1)进行了探讨，构造了大量有效的迭代算法，如Uzawa算法[1-3]、SOR-like法[4-7]、Krylov子空间法[8-9]、HSS迭代法[10-11]等。当rank(B)=r

当rank(B)=n，文献[7]构造了鞍点问题(1)的GSOR-like方法，讨论了此方法的收敛性、最优参数及相应的最小谱半径。本研究讨论当rank(B)=r

1基本概念和引理

用σ(A),ρ(A)分别表示矩阵A的谱集和谱半径。

定义1[20]设T∈n×n，当存在时，称T是半收敛的。

引理1[20]设T∈n×n，那么T半收敛当且仅当以下条件成立：

1)ρ(T)≤1;

2)如果ρ(T)=1，那么矩阵T的特征值1的所有初等因子是线性的，即rank(I-T)2=rank(I-T)；

设A∈n×n，当M可逆时，称A=M-N为A的一个分裂。考虑线性方程组Ax=b，令T=M-1N,c=M-1b，则迭代

x(k+1)=Tx(k)+c

(2)

有以下结果。

引理2[20]设A=M-N，其中M是可逆的，记T=M-1N,c=M-1b。那么对于任何初始向量x(0)，迭代(式(2))半收敛于线性方程组Ax=b的一解x*当且仅当T是半收敛的，且

x*=(I-T)Dc+(I-E)x0,E=(I-T)(I-T)D,

(3)

式(3)中，I是单位阵，(I-T)D是I-T的Drazin逆。

引理3[12]设H∈l1×l1,I∈l2×l2,l1,l2∈+,那么

(4)

半收敛当且仅当以下条件成立之一：

1)L=0,H是半收敛的；

2)ρ(H)<1。

2GSOR-like方法的半收敛性

方法1GSOR-like方法[7]:

设Q∈n×n是对称非奇异的，x(0)∈m,y(0)∈n是给定的初始向量，α,β,ω是实数，满足α>0,ω>0,α-ωβ≠0。对于k=0,1,2,…,计算

方法1等价于

(5)

式(5)中，

(6)

(7)

当rank(B)=n，鞍点问题(1)的系数矩阵是非奇异的，因此有唯一的解，文献[7]研究了收敛性质并确定了最优参数。当rank(B)=r

定理1设A∈m×m，Q∈n×n为SPD矩阵，B∈m×n，rank(B)=r

GSOR-like方法收敛于奇异鞍点问题(1)的一解x*。

证明：由引理2，只需证明方法1的迭代矩阵M(ω,α,β)是半收敛的。

(8)

(9)

定义矩阵：

(10)

式(10)中，V1∈n×r,V2∈n×(n-r)，那么

计算可得，

(11)

式(11)中，

(12)

(13)

因为

(14)

所以，ρ同时也是Q-1BTA-1B的最大特征值。证毕。

3最优迭代参数

定理2设A∈m×m，Q∈n×n为SPD矩阵，分别是Q-1BTA-1B的最大和最小特征值，那么方法1的最优半收敛因子是

最优参数是

(15)

参考文献:

[1]ELMANHC，GOLUBGH.InexactandpreconditionedUzawaalgorithmsforsaddlepointproblems[J].SiamJournalonNumericalAnalysis, 1994, 31(6):1645.

[2]BRAMBLEJH,PASCIAKJE,VASSILEVAT.AnalysisoftheinexactUzawaalgorithmforsaddlepointproblems[J].SiamJournalonNumericalAnalysis, 1997, 34(3):1072.

[3]BAIZZ,WANGZQ.OnparameterizedinexactUzawamethodsforgeneralizedsaddlepointproblems[J].LinearAlgebraanditsApplications,2008,428:2900.

[4]GOLUBGH,WUX,YUANJY.SOR-likemethodsforaugmentedsystems[J].BitNumericalMathematics, 2001,41(1):71.

[5]BAIZZ,PARLETTBN,WANGZQ.Ongeneralizedsuccessiveoverrelaxionmethodsforaugmentedlinearsystems[J].NumerischeMathematic, 2005,102(1):1.

[6]HUANGZD,ZHOUXY.OntheminimumconvergencefactorofaclassofGSOR-likemethodsforaugmentedsystems[J].NumericalAlgorithms, 2015,70(1):113.

[7]ZHOUXY.AgeneralizedSOR-likemethodforaugmentedsystems[J].JournalofZhejiangUniversityofScienceandTechnology,2015,27(6):459.

[8]SAADY.IterativeMethodsforSparseLinearSystems[M]. 2nded.Philadelphia:SocietyforIndustrialandAppliedMathematics, 2003.

[9]VANDERVORSHA.IterativeKrylovMethodsforLargeLinearSystems[M]∥Vol. 13ofCambridgeMonographsonAppliedandComputationalMathematics.NewYork:CambridgeUniversityPress,2003.

[10]BENZIM,GOLUBGH.Apreconditionerforgeneralizedsaddlepointproblems[J].SIAMJournalonMatrixAnalysisandApplications，2004, 26(1):20.

[11]BAIZZ,GOLUBGH.AcceleratedHermitianandskew-Hermitiansplittingiterationmethodsforsaddle-pointproblems[J].ImaJournalofNumericalAnalysis, 2007, 27(1):1.

[12]ZHENGB,BAIZZ,YANGX.Onsemi-convergenceofparameterizedUzawamethodsforsingularsaddlepointproblems[J].LinearAlgebraandItsApplications, 2009,431:808.

[13]ZHANGGF,WANGSS.AgeneralizationofparameterizedinexactUzawamethodforsingularsaddlepointproblems[J].AppliedMathematicsandComputation, 2013, 219(9):4225.

[14]CHAOZ,CHENG.Anoteonsemi-convergenceofgeneralizedparameterizedinexactUzawamethodforsingularsaddlepointproblems[J].NumericalAlgorithms, 2014, 68(1):95.

[15]ZHANGN,LUTT,WEIY.Semi-convergenceanalysisofUzawamethodsforsingularsaddlepointproblems[J].JournalofComputationalandAppliedMathematics, 2014, 255(285):334.

[16]LIANGZZ,ZHANGGF.Semi-convergenceanalysisoftheGPIUmethodforsingularnonsymmetricsaddle-pointproblems[J].NumericalAlgorithms, 2014, 70(1):151.

[17]BAIZZ.Onsemi-convergenceofHermitianandskew-Hermitiansplittingmethodsforsingularlinearsystems[J].Computing, 2010, 89:171.

[18]CHAOZ,ZHANGN.AgeneralizedpreconditionedHSSmethodforsingularsaddlepointproblems[J].NumericalAlgorithms, 2014, 66(2):203.

[19]WANGSS,ZHANGGF.PreconditionedAHSSiterationmethodforsingularsaddlepointproblems[J].NumericalAlgorithms, 2013, 63(3):521.

[20]BERMANA,PLEMMONSRJ.NonnegativeMatricesintheMathematicalSciences[M].Philadelphia:SocietyforIndustrialandAppliedMathematics,1994.

doi:10.3969/j.issn.1671-8798.2016.03.001

收稿日期:2016-04-10

作者简介:周小燕(1976—)，女，浙江省萧山人，副教授，硕士，主要从事计算数学研究。

中图分类号:O241.6

文献标志码:A

文章编号:1671-8798(2016)03-0177-05

On semi-convergence of a generalized SOR-like method for singular augmented systems

ZHOU Xiaoyan

(School of Sciences, Zhejiang University of Science and Technology, Hangzhou 310023, China)

Abstract:A generalized SOR-like method for singular augmented systems based on a new splitting of the iterative matrix with two real parameters α and β is presented. The semi-convergence conditions and the optimal iteration parameters and the corresponding optimal semi-convergence factor of this method are derived.

Keywords:augmented systems; GSOR-like methods; semi-convergence; the optimal parameters