“同一法”如何处理更有效*
——谈学科核心素养的基本观点

☉湖南省常德市芷兰实验学校初中部陈金红黄克勤☉湖南省常德市安乡县芦林铺中学郭作华

“同一法”如何处理更有效*
——谈学科核心素养的基本观点

☉湖南省常德市芷兰实验学校初中部陈金红黄克勤
☉湖南省常德市安乡县芦林铺中学郭作华

湘教版初中数学出现了两种间接证明方法，一个是反证法，在七年级教材中就没给“名份”的出现过，到九年级正式署名；还有一种就是同一法，当要证明某图形具有某种性质而不易直接证得时，使用此法有时可克服这种困难，一般步骤是：（1）不从已知条件入手，而是作出符合结论特性的图形；（2）证明所作的图形符合已知条件；（3）推证出所作图形与题设的其实是同一个图形.运用此法要求是苛刻的（所证命题的题设条件是唯一存在的，其结论也是唯一存在的），但效果是直观的，思路也是不易想到的！在八（下）教材中开始出现：

案例1第3页倒数第一行：直角三角形斜边上的中线等于斜边的一半.

老教材的处理：放在矩形里学习，利用了矩形的对角线互相平分且相等，现教材的处理：如图1，如果中线，则有∠DCA=∠A.由此受到启发，在图2的 Rt△ABC中，过直角顶点C作射线CD′交AB于点D′，使∠D′CA=∠A，则CD′=AD′.

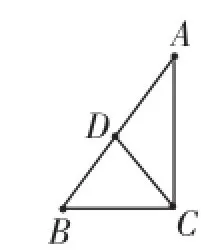
图1

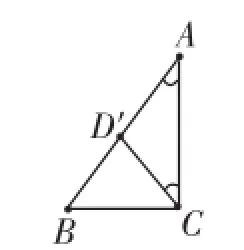
图2

这种处理是站在逆思维的基础上启发的，确实符合学生的最近发展区，但是这个“如果”前提是测量出来的，是不确定的，把一个不确定的结论作为线索，有两种可能，当它为真，还好不会引来新的“麻烦”；但当它为假时，就会产生系列错误结论！这个结局是此阶段的学生无法理解的、预测的！如果长期使用，危害是可想而知的！因为这涉及高中要学习的条件的充分性、必要性、充要性！那么如何处理呢？这正是老师们“同课异构”之处.

我们的观点：用科学研究一般探究的方式即“特例理解—一般发现—总结方法”的思路展开.

先看等腰直角三角形：思考如何得到直角三角形斜边上的中线？方法一：定义法，即取斜边中点与直角顶点连线得到的线段；方法二：运用“三线合一”，要么作斜边上的高，要么作直角顶角的平分线，再引导发现数量关系“直角三角形斜边上的中线等于斜边的一半”，此结论是“偶然”还是“必然”？

再看含30°锐角的直角三角形：思考如何得到直角三角形斜边上的中线？在以上方法的基础上，作斜边上的高，得不出斜边上的中线，为什么？（因为不能运用“三线合一”）失灵！作直角顶角的平分线，依然失灵！自然会思考为什么会失灵呢？于是回归第一个特例去发现得出中线的本质在哪？基本思路：角角关系⇔边边关系；具体是∠DCA=∠A=45°⇒AD=CD，且∠DCB=∠B=45°⇒BD= CD⇒AD=CD=BD，即说明取∠DCA=∠A时，再利用“直角三角形两锐角互余”可推出CD是斜边AB上的中线！运用此法对“含30°锐角的直角三角形”试试发现取∠DCA=∠A=30°⇒AD=CD，且∠DCB=∠B=60°⇒BD= CD⇒AD=CD=BD，成功了！

启发：说明取∠DCA=∠A时，再利用“直角三角形两锐角互余”可推出CD是斜边AB上的中线！

最后，一般地，在一般直角三角形中取∠DCA=∠A，立即可得AD=CD；利用“直角三角形两锐角互余”、“等角的余角相等”还可得∠DCB=∠B⇒BD=CD⇒AD=CD= BD，即“直角三角形斜边上的中线等于斜边的一半”是一个必然结论！

如此看来，不用同一法，依然可行且更符合八年级学生的认知心理和思维特质，特别是体现了“探究（思维和方法）”这个数学学科的核心素养；再让学生阅读书本上的证明方法时就更好理解了！做到了知其然，更知其所以然！否则给老师和学生的感觉是：“同一法”从天而降，不可思议，就像是“灌”给学生的！

因此，教材不如改变为我们上面的方法，先看几个特例再寻求其方法上的本质，最后一般发现结论就更好了！既避开了方法上的“高深莫测”，也体现了数学学科的核心素养之一：探究（思维和方法）！

案例2第14页～15页：如果三角形的三条边a，b，c满足关系a2+b2=c2，那么这个三角形是直角三角形.（勾股定理的逆定理）

老教材的处理：先尺规作图，已知两条直角边，作出满足条件的直角三角形，作为铺垫；现教材的处理：出示一段话“如果我们能构造一个直角三角形，然后证明△ABC与所构造的直角三角形全等，即可得△ABC是直角三角形”.

这种处理不符合学生的最近发展区，有点冒冒失失的心理感觉，如何想到的？这亦是老师们“同课异构”之处！也是“仿真”还原数学家探究历程的一个着力点！

我们的观点：用从科学研究到一般探究的方式，即“特例理解—一般发现—总结方法”的思路展开.

先出示题组：（1）已知Rt△ABC中，∠C=90°，三边为a，b，c且a=3，b=4，求c；（2）长度为3、4、5的三条线段能构成一个三角形吗？若能，是直角三角形吗？为什么？若不能，请说明理由.通过引导让学生自然而然地和第（1）小问联系上，和（1）中的直角三角形是同一个三角形即直角三角形，由全等三角形的判定方法“SSS”可证得！（3）已知Rt△ABC中，∠C=90°，三边为a，b，c；取线段a，b，能构成一个三角形吗？若能，是直角三角形吗？为什么？若不能，请说明理由.借助（1）、（2）积累的基本经验，不难得出“取线段a，b，能构成一个△DEF（运用三角形三边不等关系和不等式的知识），而且还是直角三角形.

如此看来，由特例入手，两图形的比较对比感悟“同一法”的脉搏，自然接轨于三角形中边的不等关系、勾股定理、二次根式、三角形全等的判定等重要基础知识和方法，再一般思考更符合八年级学生的认知心理和思维特质，体现了“探究（思维和方法）”这个数学学科的核心素养；再让学生阅读书本上的证明方法时就更好理解了！做到了知其然，更知其所以然！避免了“同一法”是帽子里突然蹦出了一只兔子的现象！

案例3第57页，B组5：证明：过三角形一边中点与另一边平行的直线必平分第三边.

老教材的处理：使用同一法.取求证边的中点，运用“过直线外一点有且仅有一条直线平行于已知直线”证出它与已知中点连线，即为要找的那条直线.

现教材教参的处理：过求证中点作已知中点所在边的平行线，过平行边所对顶点作平行边的平行线，证出两个平行四边形，再证一对三角形全等.

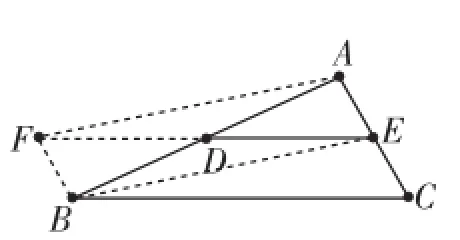
图3

更简单的处理是：已知△ABC中，D是AB的中点，DE∥BC，求证：E是AC的中点.方法一：延长ED到点F，使得FD=DE，连接AF、BF和BE；方法二：过点B作BF∥AC，与ED的延长线交于点F，连接AF和BE.都是通过得出平行四边形AEBF和平行四边形BCEF，得出AE=EC=BE，如图3，即E是AC的中点！这样处理即充分地利用了知识最近发展区（平行四边形的性质和判定或全等三角形的性质和判定），也充分利用了基本经验（见中点等倍延长法或平行线法），更符合八年级学生的认知心理和思维特质，体现了“探究（思维和方法）”这个数学学科的核心素养.

上面三个案例是新湘教版八（下）教材整册涉及“同一法”的地方，上面所述对比处理启示我们：知识点可不同处理的地方特别是方法不易想到的地方乃是“同课异构”创新教与学方法的关键处！并由此产生不同的教学指导思想、教学理念和教学模式，必映射到数学学科核心素养的培养方式和方法！

众所周知的观点是：数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析是数学核心素养.我们以为这是学术形态下的纯数学角度提出的观点；而我们中学数学是教育数学，即是从“学术形态”化成“教育形态”下的数学，因此，核心素养应该结合我们的教育对象、符合我们的教学实际，当然就一定有别于学术形态下的核心素养观，教育形态下的数学核心素养有：严肃性（讲道理：有法必依、执法必严、违法必究）、灵活性（方法多样性，条条道路通罗马）、探究性（试验、猜想、推理、抽象的科学精神）、关联性（它从来就不是孤单的），这就是我们提出的学校数学教育的核心素养观！其他学科亦可仿而效之，得出相应的教育形态下的学科核心素养！

1.义务教育课程标准实验教科书·数学（初中）［M］.长沙：湖南教育出版社，2014.

2.陈金红.你真的看过教材？［J］.湖南教育（C版），2014（12）.

3.陈金红，郭作华.你真的看过教材上的习题吗？［J］.湖南教育（D版），2015（9）.

4.陈金红，郭作华.问题演绎“活络”教材——小议教材解读的方法［J］.数学教学研究，2015（12）.

5.陈金红，郭作华.无边题海题根是岸教材是线［J］.数学教学研究，2016（2）.

6.陈金红，黄克勤，郭作华.练好常态下设计的基本功：教材解读［J］.中学数学（下），2016（1）.H

*本文系全国教育科学“十二五”规划2013年度教育部规划课题《生命课堂视野下的教学案例研究》（编号：FHB130512）的阶段性成果之一.