NOTES ON THE SPECTRAL PROPERTIES OF THE WEIGHTED MEAN DIFFERENCE OPERATOR G（u，v；∆）OVER THE SEQUENCE SPACE

Vatan KARAKAYA

Department of Mathematical Engineering，Yildiz Technical University，Davutpa¸sa，Istanbul，Turkey

E-mail∶vkkaya@yahoo.com

Ezgi ERDO˘GAN

Department of Mathematics，Marmara University，Kadiküoy，Istanbul，Turkey

E-mail∶ezgi.erdogan@marmara.edu.tr



NOTES ON THE SPECTRAL PROPERTIES OF THE WEIGHTED MEAN DIFFERENCE OPERATOR G（u，v；∆）OVER THE SEQUENCE SPACE

Vatan KARAKAYA

Department of Mathematical Engineering，Yildiz Technical University，Davutpa¸sa，Istanbul，Turkey

E-mail∶vkkaya@yahoo.com

Ezgi ERDO˘GAN

Department of Mathematics，Marmara University，Kadiküoy，Istanbul，Turkey

E-mail∶ezgi.erdogan@marmara.edu.tr

In the study by Baliarsingh and Dutta［Internat.J.Anal.，Vol.2014（2014），Article ID 786437］，the authors computed the spectrum and the fine spectrum of the product operator G（u，v；∆）over the sequence space ℓ1.The product operator G（u，v；∆）over ℓ1is definedwith xk=0 for all k＜0，where x=（xk）∈ℓ1，and u and v are either constant or strictly decreasing sequences of positive real numbers satisfying certain conditions.In this article we give some improvements of the computation of the spectrum of the operator G（u，v；∆）on the sequence space ℓ1.

Spectrum of an operator；weighted mean difference operator；sequence space 2010 MR Subject Classification47A10；47B37

1　Introduction and Preliminaries

A vector subspace of w is called a sequence space，where w is denoted by the space of all complex-valued sequences.We write ℓ∝，c，and c0for the spaces of all bounded，convergent，and null sequences，respectively，which are the Banach spaces with the sup-norm

Also，ℓ1and ℓpare denoted by the spaces of all absolutely summable and p-absolutely summable sequences，which are the Banach spaces with the norm，respectively，where 1≤p＜∞.We give a summary of literature informations concerning the spectrum and the fine spectrum of different linear operators defined by some particular limitation matrices.Wenger［1］studied the fine spectrum of the integer power of the Cesaro operator over c and Rhoades［2］generalized this result to the weighted mean methods.Gonzales［3］examined the fine spectrum of the Cesaro operator on the sequence space ℓpfor 1＜p＜∞.Also，the spectrum and the fine spectrum of the same operator over the sequence space bv∩ℓ∝was calculated by Tripathy and Saikia［4］.The spectrum and fine spectrum for the p-Cesaro operator over the space c0wasstudied by Co¸skun［5］，de Malafosse［6］，and Altay and Ba¸sar［7］studied the spectrum and the fine spectrum of the difference operator on the sequence spaces srand c0，c，respectively，where srdenotes the Banach space of all sequences x=（xk）normed byAkhmedov and Ba¸sar［8］studied the fine spectrum of the Cesaro operator over the sequence space c0.Same authors［9，10］studied the fine spectrum of the difference operator∆over the sequence spaces ℓpand bvp，where（1≤p＜∞）.Altay and Ba¸sar［11］computed the fine spectrum of the difference operator∆over the sequence space ℓpfor 0＜p＜1.Also，the fine spectrum of the generalized difference operator B（r，s）was determined over the sequence spaces ℓpand bvpby Bilgi¸c and Furkan［12］，and Tripathy and Paul［13］improved the spectrum of this operator over the vector valued sequence space c0（X）.Later，the fine spectra of the second order difference operator over the sequence spaces ℓpand bvpwas studied by Karakaya et al［14］.Karakaya and Altun［15，16］examined the fine spectra of Lacunary matrices and upper triangular double-band matrices.The spectra of factorable matrices over the sequence spaces c and ℓp，and c0were computed by Durna and Yıldırım［17］，and Rhoades and Yıldırım［18］，respectively.Recently，Ba¸sar［19］determined the spectrum and the fine spectrum of some particular limitation matrices over certain sequence spaces.Tripathy and Das［20］determined spectrum of the Rhaly operator on the sequence space bv0∩ℓ∝.More recently，Düundar and Ba¸sar［21］studied the fine spectrum of the upper triangle double band matrix∆+on the sequence space c0，and Karaisa and Ba¸sar［22］examined the fine spectra of upper triangular triple band matrices over the sequence space ℓp.Finally，Erdo˘gan and Karakaya［23］studied the spectrum of the product operator W，which is combination of weighted mean and difference matrices over the sequence spaces c and c0.

Let U and V be two Banach spaces，and L：U→V be a bounded linear operator.The set of all bounded linear operators on U into itself is denoted by B（U）.

The adjoint L∗：U∗→V∗of L is defined by

Clearly，the adjoint L∗of L is a bounded linear operator with‖L‖=‖L∗‖.

Let U 6=｛θ｝be a complex normed space and L：D（L）→U be a linear operator，where D（L）denotes the domain of L.With L we associate the operator

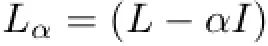
defined on the same domain D（L）as L.If Lαhas an inverse，we denote it by，that is，

and call it the resolvent operator of L.Many properties of Lαanddepend on α，and spectral theory concerned with those properties.For instance，we shall concern with the set of α values which makepossible，the boundedness ofand to know for which value of α the domain ofis dense in U.Now，we will give some basic concepts about the spectral theory（see［24］，pp.370-371］）.

A regular value α of L is a complex number such that

The resolvent set ρ（L）of L is the set of all regular values of L.Its complement σ（L）=Cρ（L）in the complex plane C is called the spectrum of L.Furthermore，the spectrum set σ（L）is union of the following three disjoint sets，which are defined as

The point spectrum：σp（L）is the set of all α∈C such that L−1αdoes not exist.A α∈σp（L）is called an eigenvalue of L；

The continuous spectrum：σc（L）is the set of all α∈C such that L−1αexists and satisfies（R3）but not（R2）；

The residual spectrum：σr（L）is the set of all α∈C such that L−1αexists but not satisfy（R3）.

To say directly，the elements α in the subspectrum σp（L）characterize some lack of injectivity，those in σr（L）some lack of surjectivity，and those in σc（L）some lack of stability of the operator L−αI.（see［25］，p.24）

Letµand γ be two sequence spaces and A=（ank）be an infinite matrix of real or complex numbers ank，where n，k∈N.Then，we say that A defines a matrix mapping fromµinto γ，and we denote it by writing A：µ→γ if for every sequence x=（xk）∈µ，the sequence Ax=｛（Ax）n｝，the A-transform of x，is in γ，where

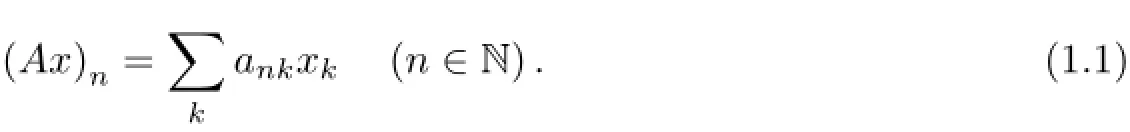
By（µ：γ），we denote the class of all matrices A such that A：µ→γ.Thus，A∈（µ：γ）if and only if the series on the right-hand side of（1.1）converges for each n∈N and every x∈µ，and we have Ax=｛（Ax）n｝∈γ for any x∈µ.

Lemma 1.1（［26］，p.253，Theorem 34.16）The matrix A=（ank）gives rise to a bounded linear operator T∈B（ℓ1）from ℓ1to itself if and only if the supremum of ℓ1norms of the columns of A is bounded.

The operator norm of T is the supremum of the ℓ1norms of the columns.

Lemma 1.2（［27］，p.59）T has a dense range if and only if T∗is one to one.

Lemma 1.3（［27］，p.60）The adjoint operator T∗of T is onto if and only if T has a bounded inverse.

The spectrum of the product operator G（u，v；∆）which is multiplication of weighted mean and difference matrices over the sequence space ℓ1is determined by Baliarsingh and Dutta［28］.To introduce some difference sequence spaces the operator G（u，v；∆）was defined and studied by Polat et al［29］，and Erdo˘gan and Karakaya［23］studied the spectrum of the same operator over the sequence spaces c and c0.The product operator G（u，v；∆）over ℓ1is definedwith xk=0 for all k/∈N0，where N0denotes the set of all non-negative integers，x=（xk）∈ℓ1，and（uk）and（vk）are two bounded either constant or strictly decreasing sequences of positive real numbers such that uk6=0 and vk6=0 for all k，and

The product operator G（u，v；∆）can be expressed by the triangle matrix G（u，v；∆）=（gnk）defined by

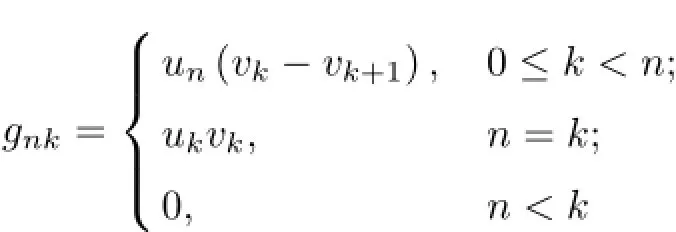
for all k，n∈N0.

We summarize the main results concerning the spectrum of the product operator G（u，v；∆）on the sequence space ℓ1as stated in［28］as follows.

Theorem 1.4（［28］）The operator G（u，v；∆）：ℓ1→ℓ1is a linear operator and

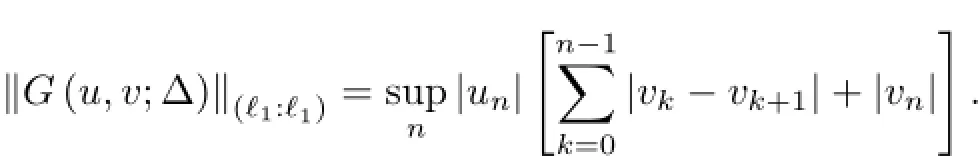
Theorem 1.5（［28］）The spectrum of G（u，v；∆）over the sequence space ℓ1is given by

Theorem 1.6（［28］）The point spectrum of the operator G（u，v；∆）over ℓ1is given by

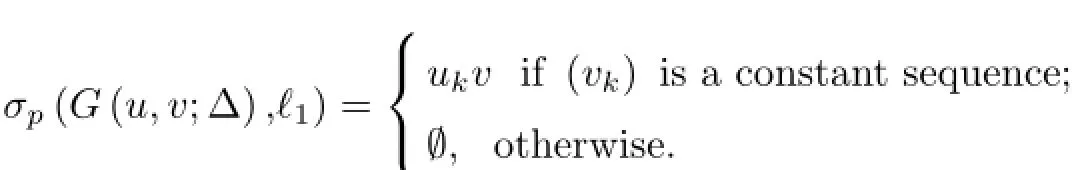
Theorem 1.7（［28］）The point spectrum of the dual operator（G（u，v；∆））∗over the sequence space ℓ∗1～=ℓ∝is given by

Theorem 1.8（［28］）The residual spectrum of the operator G（u，v；∆）over the sequence space ℓ1is given by

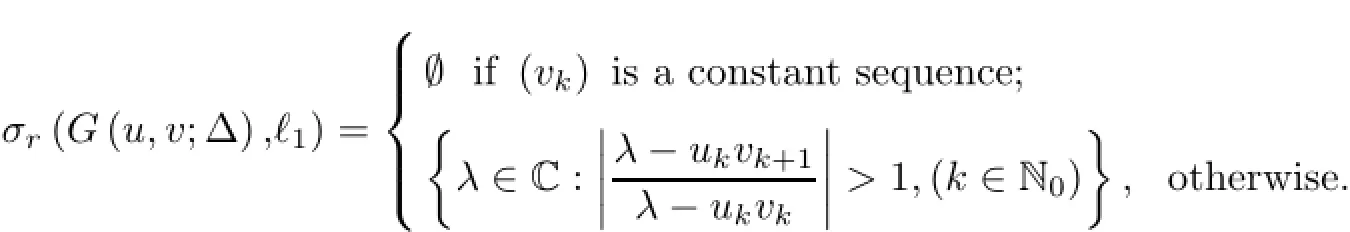
Theorem 1.9（［28］）The continuous spectrum of the operator G（u，v；∆）over the sequence space ℓ1is given by

However，these results given in［28］need some corrections.This will be shown by a counterexample in next section.Then，we prove the corrected results in Section 3.

2　A Counterexample

Let us assume that（uk）=u is a constant sequence of positive real numbers and（vk）= It is obvious that the sequence（uk）satisfies condition（1.2）and the sequence（vk）is a strictly decreasing sequence of positive real numbers satisfying condition（1.3）.Indeed，

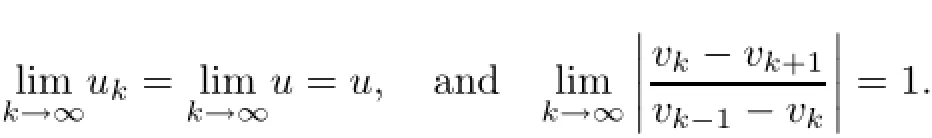
We can show that G（u，v；∆）/∈（ℓ1：ℓ1）for these sequences.For the sequence（vk）defined above，the matrix G（u，v；∆）=（gnk）is in the following form

By Lemma 1.1，the operator G（u，v；∆）∈（ℓ1：ℓ1）if sup

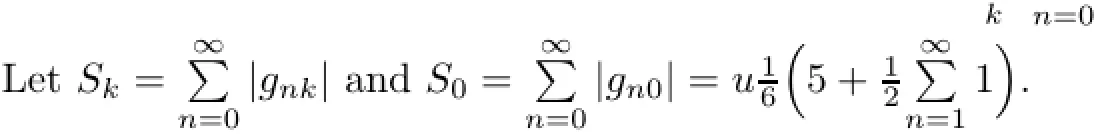
Therefore，it is divergent.So，we have a contradiction，thus the ℓ1norms of the columns of G（u，v；∆）are not bounded.

Hence，there is no matrix which gives rise to a bounded linear operator T∈B（ℓ1）from ℓ1to itself when the sequences（uk）and（vk）are a constant and a strictly decreasing sequence of positive real numbers，respectively.

If the sequence（vk）is constant，then G（u，v；∆）is a diagonal matrix.So，it always satisfies Lemma 1.1.But if the sequ?ence（?vk）is strictly decreasing，then we conflict with Lemma 1.1.（if we choose（uk）=（vk）=，then we get G（u，v；∆）∈/（ℓ1：ℓ1）.）To provide Lemma 1.1，the sequence（uk）should be in ℓ1when the sequence（vk）is strictly decreasing.The necessity of this requirement can be seen as follows：

can be proved if and only if by considering（uk）∈ℓ1.

For brevity，we use the following abbreviations：

Usd：The sequence（uk）is strictly decreasing，

Uc：The sequence（uk）is constant，

Vsd：The sequence（vk）is strictly decreasing，

Vc：The sequence（vk）is constant.

Then，we have three cases for the matrix operator

Another correction is about the norm of the operator.By Lemma 1.1，

But the authors compute the supremum of the ℓ1norms of the rows in［28］.

Because of the errors in the norm，there are mistakes in the proofs of the spectrum sets. Next，we provide the corrected results.

3　Corrected Results for the Subspectrums of the Weighted Mean Difference Operator G（u，v；∆）Over the Space ℓ1

In this section，we introduce corrected versions of the subspectrums given in［28］on the space ℓ1for the sequences in（2.1）.As the sequences（uk）and（vk）are monotone and bounded and the results are valid，in general，for either constant or strictly decreasing sequence of positive real numbers，so there is no need the conditions（1.2）and（1.3），respectively.

Let us define the sets D and E as

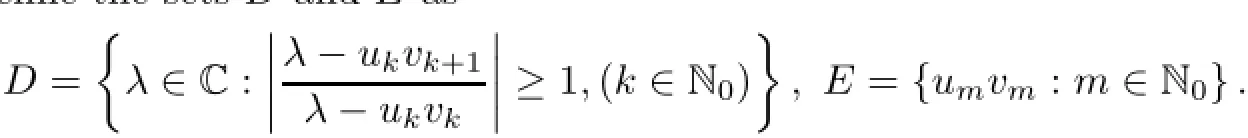
Theorem 3.1G（u，v；∆）：ℓ1→ℓ1is a bounded linear operator and

ProofBy applying Lemma 1.1，we get the proof.

The norm differs according to situation of the sequences（uk）and（vk）.We now give some special cases.

Case 1If Usd and Vsd（so（uk）∈ℓ1），then we have

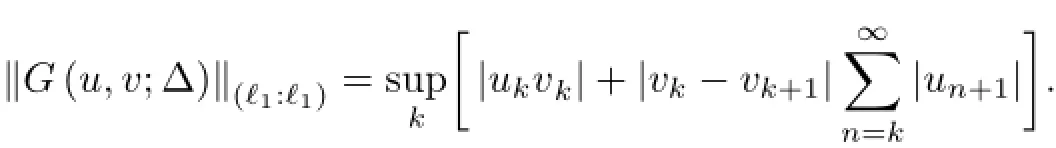
Case 2If Usd and Vc，then

Case 3If Uc and Vc，then we have

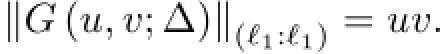
Theorem 3.2

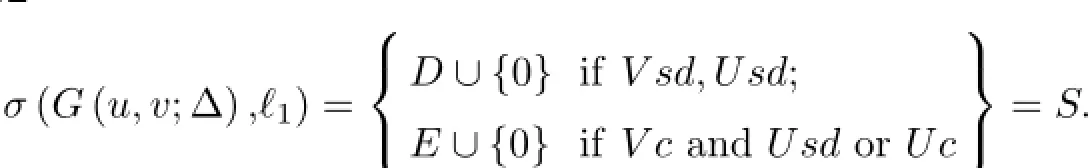
ProofFirst we prove that（G（u，v；∆）−λI）−1exists and is in（ℓ1：ℓ1）for λ/∈S and then show that the operator G（u，v；∆）−λI is not invertible for λ∈S.As the spectrum changes according to the sequence（vk），we give the proof in two cases.

Case 1Let Vsd.Then it is known that u=（uk）∈ℓ1.

Let λ/∈S.As λ 6=u0v0，then G（u，v；∆）−λI is triangle and has an inverse.Solving the equation（G（u，v；∆）−λI）x=y for x in terms of y gives the matrix of［G（u，v；∆）−λI］−1=（hnk）

Thus，we get

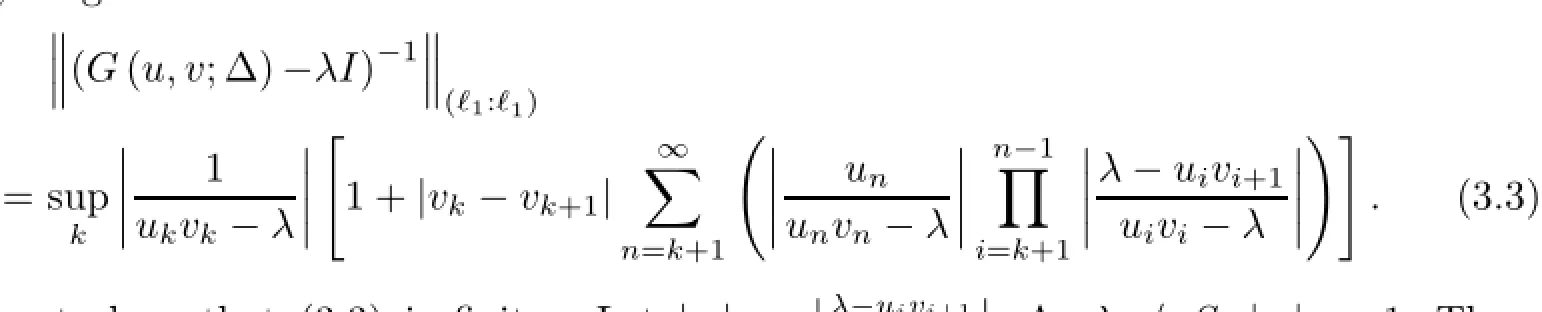
We must show that（3.3）is finite.one can find a q such that sup |qi|=|q|＜1.As the sequences（un）and（vk）are bounded，

Hence，we obtain，for λ∈/S，（G（u，v；∆）−λI）−1∈（ℓ1：ℓ1）.

Conversely，consider λ∈S.If λ=0，then the operator is not onto.To s?how that，?choose y=u=（un）∈ℓ1.Solving（G（u，v；∆）−0I）x=u，we obtainAs the operator is not onto，it is not invertible.For other values of λ in S，G（u，v；∆）−λI is triangular，the inverse operator（G（u，v；∆）−λI）−1exists，and one can see by（3.3）that

Case 2Let us assume that Vc.As G（u，v；∆）−λI is a diagonal matrix，then the operator（G（u，v；∆）−λI）−1exists.Solving the equation（G（u，v；∆）−λI）x=y for x in terms of y gives the matrix of（G（u，v；∆）−λI）−1.The nthrow turns out to bein theplace for k=n and zero otherwise.Then，we obtain

Hence，for λ/∈S，（G（u，v；∆）−λI）−1∈（ℓ1：ℓ1）.

Now，suppose λ∈S.If λ=0，then the operator is not onto.As in Case 1，x=（xn）=Let λ=umv∈S.As（G（u，v；∆）−λI）x=θ implies x 6=θ for λ=umv，G（u，v；∆）−λI：ℓ1→ℓ1is not injective，and also has not a dense range.Hence，it is not invertible.This completes the proof.

Theorem 3.3

ProofFor a sequence x 6=θ in ℓ1，suppose that G（u，v；∆）x=λx.

Case 1Let Vsd.Then，by solving the system of linear equations

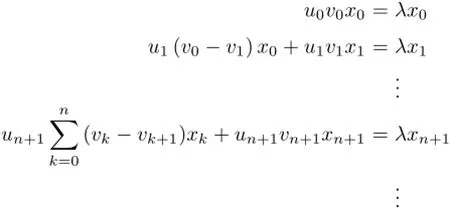
we find that if xmis the first non-zero entry of the sequence x=（xn），then λ=umvm.We obtain，for all p∈N，

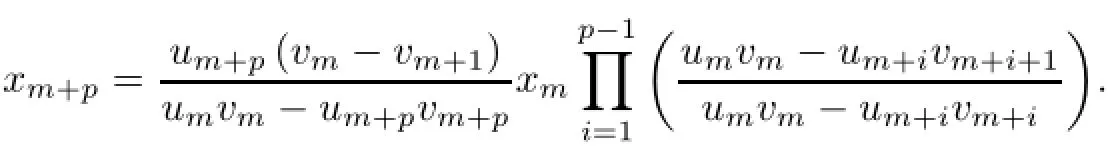
So，x=（xn）must be in ℓ1.

We know that if Vsd，then the sequence（uk）is in ℓ1.Then，we obtain

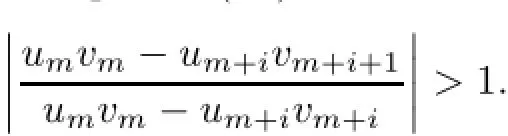
Thus for n→∞，x=（xn）/∈c0.As ℓ1⊂c0，then x=（xn）/∈ℓ1. Case 2Let Vc.Then，by solving the system of linear equations，

If xmis the first nonzero entry of the sequence x=（xn），then we get λ=umv and x=（0，0，···，0，xm，0，···）∈ℓ1.

If T：ℓ1→ℓ1is a bounded linear operator with a matrix S，then it is known that the adjoint operatoris defined by the transpose of the matrix S.The dual space of ℓ1is isomorphic to ℓ∝.

It follows that，for λ=umvm，the first m+1 elements are nonzero in the sequence f=（fn）. This means that f=（f0，f1，···，fm，0，···）and for λ=umvm，we get the（m−l）term of the sequence f as follows：

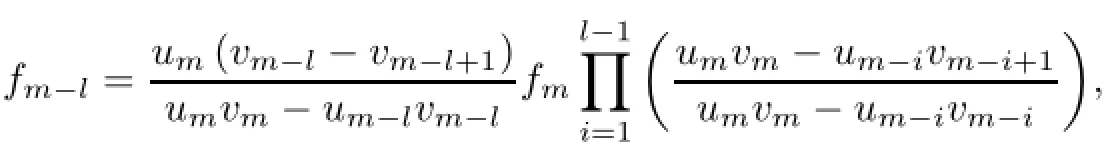
where l=0，1，···，m.

As the sequences（uk）and（vk）are bounded，one can find J and H such that

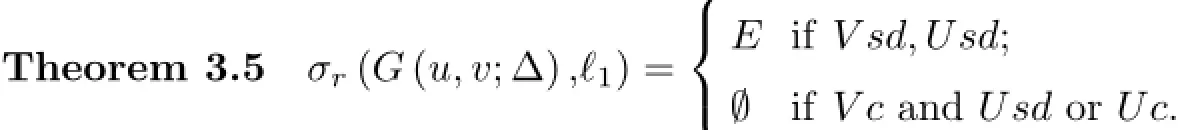
ProofIt must be shown that the operator G（u，v；∆）−λI has an inverse and

Case 1Let us assume Vsd.For λ=umvm，as the operator is one to one，then it has an inverse.From Theorem 3.4，（G（u，v；∆））∗−λI is not one to one.So，by applying Lemma 1.2，we get the result.

Case 2For Vc，from Theorem 3.4 and Lemma 1.2，we obtainfor λ=umv.As the operator G（u，v；∆）−λI is not one to one for λ=umv from Theorem 3.3，we obtain σr（G（u，v；∆），ℓ1）=∅.

References

［1］Wenger R B.The fine spectra of Holder summability operators.Indian J Pure Appl Math 6，1975：695-712

［2］Rhoades B E.The fine spectra for weighted mean operators.Pacific J Math，1983，104（1）：219-230

［3］Gonzales M.The fine spectrum of the Cesaro operator in ℓp，（1＜p＜∞）.Arch Math，1985，44：355-358

［4］Tripathy B C，Saikia P.On the spectrum of the Cesaro oprator C1on bv∩ℓ∝.Math Slovaca，2013，63（3）：563-572

［5］Co¸skun C.The spectra and fine spectra for p-Cesaro operators.Turkish J Math，1997，21：207-212

［6］de Malafosse B.Properties of some sets of sequences and application to the spaces of bounded difference sequences of orderµ.Hokkaido Math J，2002，31：283-299

［7］Altay B，Ba¸sar F.On the fine spectrum of the difference operator∆on c0and c.Inform Sci，2004，168：217-224

［8］Akhmedov A M，Ba¸sar F.On the fine spectrum of the Cesaro operator in c0.Math J Ibaraki Univ，2004，36：25-32

［9］Akhmedov A M，Ba¸sar F.On the spectra of the difference operator∆over the sequence space ℓp.Demonstratio Math，2006，39（3）：585-595

［10］Akhmedov A M，Ba¸sar F.On the fine spectra of the difference operator∆over the sequence space bvp，（1≤p＜∞）.Acta Math Sin（Engl Ser），2007，23（10）：1757-1768

［11］Altay B，Ba¸sar F.The fine spectrum and the matrix domain of the difference operator∆on the sequence space ℓp，（0＜p＜1）.Commun Math Anal，2007，2：1-11

［12］Bilgi¸c H，Furkan H.On the fine spectrum of generalized difference operator B（r，s）over the sequence spacesℓpand bvp.Nonlinear Anal，2008，68：499-506

［13］Tripathy B C，Paul A.Spectra of the operator B（f，g）on the vector valued sequence space c0（X）.Bol Soc Parana Mat（3），2013，31（1）：105-111

［14］Karakaya V，Manafov M Dzh，S¸im¸sek N.On the fine spectrum of the second order difference operator over the sequence spaces ℓpand bvp.Math Comput Modelling，2012，55（3）：426-436

［15］Altun M，Karakaya V.Fine spectra of lacunary matrices.J Commun Math Anal，2009，7（1）：1-10

［16］Karakaya V，Altun M.Fine spectra of upper triangular double-band matrices.J Comput Appl Math，2010，234：1387-1394

［17］Durna N，Yıldırım M.Subdivision of the spectra for factorable matrices on c and ℓp.Math Commun，2011，16：519-530

［18］Rhoades B E，Yıldırım M.The spectra and fine spectra of factorable matrices on c0.Math Commun，2011，16：265-270

［19］Ba¸sar F.Summability Theory and Its Applications.Bentham Science Publishers，e-books，Monographs，Istanbul，2012

［20］Tripathy B C，Das R.Spectra of the Rhaly operator on the sequence space bv0∩ℓ∝.Bol Soc Parana Mat（3），2014，32（1）：263-275

［21］Düundar E，Ba¸sar F.On the fine spectrum of the upper triangle double band matrix∆+on the sequence space c0.Math Commun，2013，18：337-348

［22］Karaisa A，Ba¸sar F.Fine spectra of the upper triangular triple band matrices over the sequence spaceℓp，（0＜p＜∞）.Abstr Appl Anal，2013，2013.ID 342682

［23］Erdo˘gan E，Karakaya V.On spectral properties of a new operator over sequence spaces c and c0.Acta Math Sci Ser B Engl Ed，2014，34（5）：1481-1494

［24］Kreyszig E.Introductory Functional Analysis with Applications.New York：John Wiley and Sons Inc，1978

［25］Appell J，Pascale E，Vignoli A.Nonlinear Spectral Theory.de Gruyter Ser Nonlinear Anal Appl，Walter de Gruyter·Berlin·New York，2004

［26］Wilansky A.Summability Through Functional Analysis.North-Holland Mathematics Studies，Vol 85.Amsterdam：North Holland，1984

［27］Goldberg S.Unbounded Linear Operators.Mc Graw-Hill Book Comp，1966

［28］Baliarsingh P，Dutta S.On the spectral properties of the weighted mean difference operator G（u，v；∆）over the sequence space ℓ1.Internat J Anal，2014，2014

［29］Polat H，Karakaya V and S¸im¸sek N.Difference sequences spaces derived by using a generalized weighted mean.Appl Math Lett，2011，24：608-614

September 24，2014；revised January 11，2015.