FREDHOLM OPERATORS ON THE SPACE OF BOUNDED SEQUENCES∗

Egor A.ALEKHNO Faculty of Mechanics and Mathematics，Belarussian State University，Minsk，Belarus E-mail∶alekhno@bsu.by



FREDHOLM OPERATORS ON THE SPACE OF BOUNDED SEQUENCES∗

Egor A.ALEKHNO Faculty of Mechanics and Mathematics，Belarussian State University，Minsk，Belarus E-mail∶alekhno@bsu.by

Necessary and sufficient conditions are studied that a bounded operator Tx=on the space ℓ∝，where，is lower or upper semi-Fredholm；in particular，topological properties of the set，···｝are investigated.Various estimates of the defect d（T）=codimR（T），where R（T）is the range of T，are given.The case ofwhere dn∈R and x≥0 are extreme points of the unit ball，that is，tn∈βN，is considered.In terms of the sequence｛tn｝，the conditions of the closedness of the range R（T）are given and the value d（T）is calculated.For example，the condition｛n∶0＜|dn|＜δ｝=∅for some δ is sufficient and if for large n points tnare isolated elements of the sequence｛tn｝，then it is also necessary for the closedness of R（T）（tn0is isolated if there is a neighborhood U of tn0satisfying tn∈/U for all n/=n0）.If｛n∶|dn|＜δ｝=∅，then d（T）is equal to the defect δ｛tn｝of｛tn｝.It is shown that if d（T）=∞and R（T）is closed，then there exists a sequence｛An｝of pairwise disjoint subsets of N satisfying χAn∈/R（T）.

Fredholm operator；space ℓ∝；Stonecompactification βN

2010 MR Subject Classification47A53；47B37；54D35

1　Introduction

Let X and Y be Banach spaces.As usual，L（X，Y）will denote the space of all（bounded，linear）operators and K（X，Y）the space of all compact operators from X into Y.

Definition 1.1For an operator T∈L（X，Y），the null space N（T）and the range R（T）of T［1，p.155］are the sets

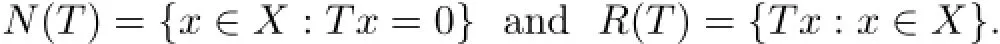
The dimension of N（T）is called the nullity of T and is denoted n（T）.The codimension of R（T）is called the defect of T and is denoted d（T）.

Definition 1.2An operator T is said to be Fredholm［1，p.156］if its nullity n（T）and defect d（T）are both finite.

The collection of all Fredholm operators from X into Y will be denoted by Φ（X，Y）；as usual，we shall write Φ（X）instead of Φ（X，X）（analogously，for example，for L（X）and K（X））.

One of most important characterizations of Fredholm operators is the following Atkinson's theorem［1，p.161］establishing the connection between Fredholm and compact operators：anoperator T from X into Y is Fredholm if and only if there exist operators K1∈K（X），K2∈K（Y），and S1，S2∈L（Y，X）such that

Now，let us consider the Banach space ℓ∝of all bounded sequences equipped with the sup-norm.Every operator T on ℓ∝can be represented in the form

On the other hand，an operator T on ℓ∝defined by a sequenceis compact［3］if and only if the setis relatively compact inTherefore，the compactness of the operator T can be characterized in terms of geometrical properties of the setTaking into account the connection which exists between Fredholm and compact operators（see（1.1）），the hypothesis arises that Fredholm operators onalso can be characterized in terms of geometrical properties of the set，···｝.The main purpose of this article is to obtain some results in this direction.

Definition 1.3A bounded sequenceof functionals inis said to be Fredholm if the operator T defined by this sequence is Fredholm.

We also recall the following two notions（see［2，p.33］）.

Definition 1.4An operator T∈L（X，Y）is said to be upper semi-Fredholm if n（T）＜∞and R（T）is closed and is said to be lower semi-Fredholm if d（T）＜∞.

We mention at once that by Kato's theorem［1，p.156］，the relation d（T）＜∞implies the closedness of R（T）.The collection of all upper and lower semi-Fredholm operators from X into Y will be denoted by Φ+（X，Y）and Φ−（X，Y），respectively.Obviously，the identity Φ（X，Y）=Φ−（X，Y）∩Φ+（X，Y）is valid and it suggests an idea that，first of all，conditions of necessary and sufficient should be found under which either the inclusion T∈Φ−（ℓ∝）or the inclusion T∈Φ+（ℓ∝）holds.Below the second and third sections are devoted to these problems，respectively.In particular，the conditions under which R（T）is closed should be investigated and the results in this direction are included in Section 2.This section has two subsections.In the first one，we consider the general case of an arbitrary operator T on ℓ∝.When we specialize the Fredholm properties of operators to the class of almost diagonal operators，we obtain much sharper results.This task is taken in Section 2.2.

By analogy to the notion of Fredholm sequence，we introduce the following two notions.

Definition 1.5A bounded sequenceiis said to be lower（upper）semi-Fredholm if the operator T defined bys lower（upper）semi-Fredholm.

A compact perturbation of a Fredholm operator and a lower（upper）semi-Fredholm operator remains Fredholm，that is，for example，the relations T∈Φ（X，Y）and K∈K（X，Y）imply T+K∈Φ（X，Y）；in particular，for every sequencesuch that the setis relatively compact and for every Fredholm sequencethe sequenceis also Fredholm.In particular，a Fredholm sequence can be changed on a finite number of elements and still remains Fredholm.

For any unexplained terminology，notions，and elementary properties of the theory of Fredholm operators，we refer to［1，2，7］，and of theory ordered linear spaces to［1，5，11］.For information on weak topologies on Banach spaces，please refer to［5］（see also［6］）.More details on Stone-˘Cech compactification and on topological notions related to it can be found in［9］. For the simplicity，throughout this article，all spaces will be assumed real.Furthermore，the case of a sequence x=（x1，x2，···）as an element of the space ℓ∝and the case of a sequence）of elements in some set A of an arbitrary nature should differ.In the sequel，unless stated otherwise，considering some topology on a Banach space，we will assume the norm topology.For an arbitrary subset B⊆N，the characteristic sequence χBof B is defined by（χB）n=1 if n∈B and（χB）n=0 if n/∈B.We put e=χNand en=χ｛n｝，where n∈N. Functionalson ℓ∝is defined by=xn.An operator PBon ℓ∝is defined via the formula PBx=χB·x.Next，for an arbitrary sequence x∈ℓ∝，the support of x is the subset of N defined via the formula supp x=｛n∈N：xn6=0｝.Finally，recall that in an arbitrary Riesz space E，the modulus of an element y∈E，denoted by|y|，is the least upper bound of the set｛y，−y｝.Two elements y and z in E are said to be disjoint whenever the greatest lower bound of the set｛|y|，|z|｝is equal to the zero element.

2　Conditions that T∈Φ−（ℓ∞）

2.1The case of an arbitrary operator T

We start with the next auxiliary result.

Lemma 2.1Let aij∈R for all i，j∈N and let

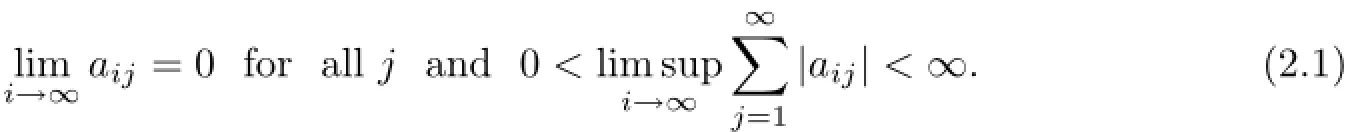
Then，the subspace of ℓ∝is closed，contains the space c0of all sequences converging to zero，and is not complemented；in particular，codimX=∞.

ProofConsider a sequence｛xn｝in X and assume that xn→x in ℓ∝.Fix ǫ＞0 and putChoose an index n0satisfying the inequality‖x−and find an index i0satisfying the inequalityfor all i≥i0.Then，

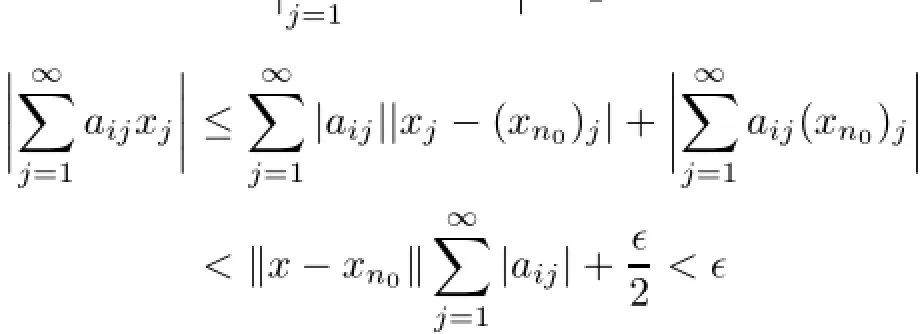
for all i≥i0.Thus，=0 and the closedness of X has been established.Next，by the first relation of（2.1），en∈X for all n and，hence，c0⊆X.

Now，assume that the subspace X is complemented.This means that there exists a continuous projection P on ℓ∝having the range R（P）=X.Define functionalsBecausefor all x∈X，we haveUsing Phillips'lemma［11，p.130］，we obtain

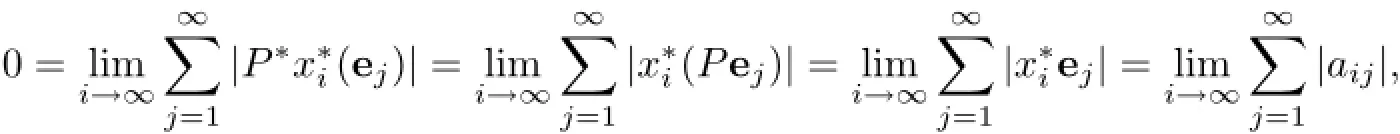
which is a contradiction with the second relation of（2.1）.

In the next theorem，the sufficient conditions are given under which a sequence or an operator is lower semi-Fredholm.Recall first that，by Grothendieck's theorem［5，p.211］，for a sequencethe convergenceis equivalent to the convergence

ProofLet T be an operator defined by｛｝and let X be a space defined by relation（2.2）. Clearly，R（T）⊆X.By the preceding lemma，codimR（T）=∞，that is，

Corollary 2.3Suppose that aij∈R for i，j∈N，relation（2.1）is valid，and the identity holds for some number λ 6=0 and for all i.If｛｝is a bounded sequence insuch that the sequenceconverges weakly，then｛is not lower semi-Fredholm.

Corollary 2.4A bounded sequencesuch that the sequenceweakly converges is not lower semi-Fredholm.

Remark 2.5（a）The following“operator”form can be given for Theorem 2.2：Let T and A be operators on ℓ∝and suppose that A is an integral operator，in other words，A has a matrix representation satisfying

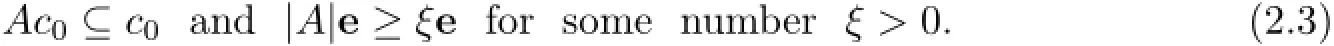
If AT（ℓ∝）⊆c0，then T/∈Φ−（ℓ∝）（where|A|is the modulus of the operator A）.It should be noted that the conditions（2.3）does not imply the inclusion A∈Φ−（ℓ∝）.Indeed，it suffices to consider the Cezaro operator C on the space ℓ∝defined by the sequencethatfor x∈ℓ∝.Using the identity=C，whereis the restriction of the adjoint C∗of C to ℓ1，it is easy to see that R（C）is not closed.

（b）There exists another less“geometric”manner of the proof of Theorem 2.2.Indeed，let T∈Φ−（ℓ∝）be an operator defined byThen，its adjoint operatorConsequently［8］，there is an index n0∈N such that the sequenceis equivalent to the sequence，that is，In other words，there exists an isomorphism U from the closed span of the setinto the closed span of thesuch that UOn the other hand，obviously，i→∞（we use the notations of Theorem 2.2）.Hence，using the identity

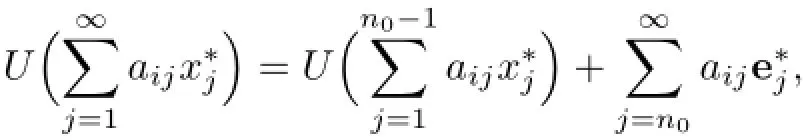
Now，we turn to necessary conditions under which a sequence or an operator are lower semi-Fredholm.First of all，we recall that the subspace

of ℓ∝，where Lin denotes the span of a given set，is dense in ℓ∝.Therefore，if Y is an arbitrary closed subspace of ℓ∝，then the condition codimY=∞is equivalent to this：for every k∈N，there exist subsets A1，···，Ak⊆N such that χA1，···，χAkare linearly independent and the relation Y∩Lin｛χA1，···，χAk｝=｛0｝holds.In particular，such a system of sets can be found if Y=R（T）and the range R（T）of an operator T on ℓ∝is closed while T/∈Φ−（ℓ∝）. Consequently，one of the approaches to the study of necessary conditions under which a sequence or an operator is lower semi-Fredholm is to obtain conditions under which such sets A1，···，Akexist.To this end，we introduce the following two notions.Below，Lin and co are the σclosure of the span and the convex hull of a given subset of，respectively.

Definition 2.6A system（A1，···，Ak）of nonempty pairwise disjoint subsets of N is said to be T-inaccessible，where an operator T on ℓ∝is defined by a sequence，if

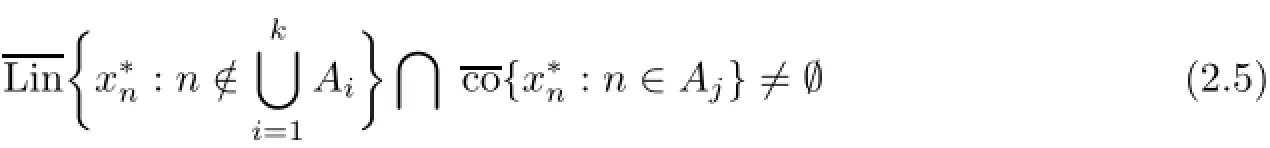
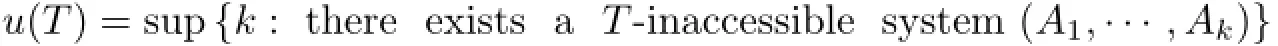
（if such system does not exist，we put u（T）=0）is called the inaccessibality index of T.

It should be at once noted that systems（A1，···，Ak）satisfying，for example，the relation

where aff is the affine hull，can also be considered.

Proposition 2.7For an operator T on ℓ∝defined by a sequence｛x∗n｝and a system（A1，···，Ak）of nonempty pairwise disjoint subsets of N，the following statements hold：

（a）A system（A1，···，Ak）is T-inaccessible if and only if for every index j=1，···，k，there exists no element x∈ℓ∝such that

i=1

（b）If（A1，···，Ak）is T-inaccessible，then R（T）∩Lin｛χA1，···，χAk｝=｛0｝；

（c）The inequality u（T）≤d（T）holds.

Proof（a）To check the necessity，consider a functional x∗belonging to the intersection（2.5）.If there exists an element x∈ℓ∝satisfying（2.6），then，x∗nx≥1 for n∈Ajand，hence，x∗x≥1，x∗nx=0 for n∈/∪kAiand，hence，x∗x=0，which is impossible.For the

i=1 converse，assume that for some j=1，···，k，relation（2.5）does not hold.Both sets in the left part of（2.5）are convex and σ）-closed and，moreover，according to Alaoglu's theorem［5，p.141］，the second one is σ）-compact.By the classical Separation Theorem［5，p.136］，there exists an element x∈ℓ∝satisfying（2.6），a contradiction.

（b）Assume that for some x∈ℓ∝，the identity Tx=holds with λi∈R.Then，for an arbitrary index j=1，···，k，we have=λjfor n∈Ajand=0 for n∈/∪k

Ai.

i=1 By（a），for every fixed index j，we get λj=0 and，hence，Tx=0.

Part（c）follows immediately from（b）.

Corollary 2.8If an operator T∈Φ−（ℓ∝），then u（T）＜∞.

It is not known if the identity u（T）=d（T）holds for every operator T on ℓ∝.Some of the results below（see，for example，Example 2.9，Theorem 2.10，and the identity（2.18）of Theorem 2.17（d））will provide some evidence to expect the validity of this conjecture. The affirmative answer should have meant that the condition u（T）＜∞characterizes the lower semi-Fredholm operators.In particular，it is not known if there exists an example of an operator T satisfying 0=u（T）＜d（T）.Next，according to Proposition 2.7（a），the identity u（T）=0 implies that for every subset A⊆N，there exists an element xA∈ℓ∝with the properties TxA≥χAand supp TxA⊆A；in particular，x｛n｝6=0 for all n∈N.If，in this case，the operator T is interval preserving，that is，［5，p.89］T［0，x］=［0，Tx］for all 0≤x∈ℓ∝，and R（T）is closed，then χA∈R（T）for all A⊆N and，henceThus，d（T）=0 and，under these conditions，we have the identity u（T）=d（T）.

Due to the remarks above，the next example is interesting.

Example 2.9（a）Let us consider the sequencein the spacedefined by=andfor n≥2.By Corollary 2.4，is not lower semi-Fredholm.On the other hand，by Proposition 2.7（a），every system（A1，···，Ak）of pairwise disjoint subsets of N such that each of A1，···，Akcontains an interval of a sufficiently large length is T-inaccessible，where T is an operator defined by｛x∗n｝.Therefore，u（T）=d（T）=∞.Whereas Theorem 2.2 distinguishes the class of operators with the property that d（T）=∞，it is not clear how u（T）can be characterized in general.

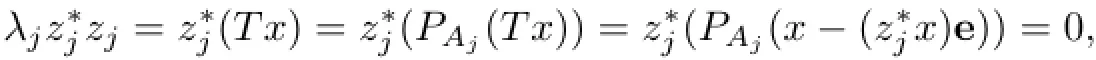
that is，λj=0，as required.Finally，d（T）=∞.However，in the general case，it is not even known if the inequality u（T）＞0 is valid.It can be shown that the identity u（T）=0 implies the relation=0 for all n∈Ajand，hence，all sets Ajmust be infinite.

In view of Proposition 2.7（b），the equality u（T）=∞implies that for an arbitrary number k∈N，there exist pairwise disjoint sets A1，···，Aksatisfying χAj∈/R（T）for all j=1，···，k. For d（T）=∞，Theorem 2.10 below improves this result.

Before proceeding further，we recall that every sequence x∈ℓ∝can be considered as a continuous function on the set N with the discrete topology.Therefore，this function extends uniquely to a continuous function xb from thecompactification βN of N to R.Obviously，this extension defines an isometric isomorphism from ℓ∝onto the space C（βN）of all continuous functions on βN which preserves algebraic operations and lattice operations.Consequently，every functional on the space C（βN）defines a functional on ℓ∝.In particular，for every point t∈βN，there exists a functional∈such that= xb（t）for all x∈ℓ∝. Evidently，≥0.If t=n，then=.For arbitrary points s，t∈βN，two functionalsandare disjoint（in the Banach lattice）if and only if s 6=t.Moreover，a positive functionalhas the form x∗tfor some t∈βN if and only if x∗is an extreme point of the closed unit ball Bℓ∗∝of ℓ∗

∝.Next，by Riesz Representation Theorem，for every functional

Theorem 2.10Let Y be a closed subspace of ℓ∝such that codimY=∞.Then，there exists a sequence｛An｝of pairwise disjoint subsets of N satisfying χAn∈/Y for all n.

In particular，such sequence exists if Y=R（T），where T∈L（ℓ∝），R（T）is closed，and d（T）=∞.

ProofFirst of all，we mention that if for some subset B⊆N and some functional x∗∈Y⊥，the relation∩suppµx∗6=∅holds，where=｛0｝｝and suppµx∗is the support of the measureµx∗，then for some subset A⊆B，the relation χA∈/Y holds.Indeed，if for every subset A⊆B，the inclusion χA∈Y is true，then x∗χA=0 and，hence，is a lattice homomorphism，we getThus，=0，that issuppµx∗=∅，a contradiction.

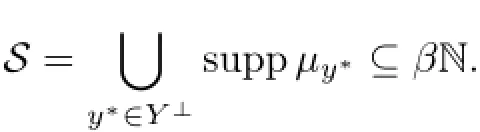
Let us consider the setIf card S=m＜∞，that is，S=｛s1，···，sm｝，then we have Y⊥⊆Linand，hence，the space Y⊥is finite dimensional.The closedness of the subspace Y guarantees the identity codimY=dimY⊥.Thus，codimY＜∞，which is impossible.Hence，cardS=∞.

Next，we will show that if｛B1，···，Bk｝is a partition of N into nonempty pairwise disjoint sets B1，···，Bk，then we can find an index i0∈｛1，···，k｝and sets B′and B′′satisfying the relations Bi0=B′∪B′′，B′∩B′′=∅，and χB′，χB′′∈/Y.To verify this，using the relations=∅for i 6=j，we find points s′，s′′∈S，s′6=s′′，and a set

Now，we define the set B11=N.As showed above，there exist sets B21and B22satisfying B11=B21∪B22，B21∩B22=∅，and χB21，χB22/∈Y.One of these sets is infinitely reducible，that is，it can be represented in a form of the union of two disjoint sets B31and B32satisfying χB31，χB32/∈Y and at least one from two new sets B31and B32also will be reducible by a similar manner，and after the decomposition of this new set，we obtain at least one reducible set again，moreover continuing this process further，we will obtain at least one reducible set every time.Thus，one of set B21or B22is infinitely reducible.Without loss of generality，we can assume that it is B22and put A1=B21.Next，decompose B22as B22=B31∪B32. Again，if B32is infinitely reducible，then we put A2=B31and decompose B32.Iterating this procedure yields a sequence｛An｝as required.

The proven theorem does not hold without the assumption about the closedness of Y. Indeed，to see this，it suffices to check the identity codimY0=∞（see（2.4））；although，obviously，codimY0=0.To this end，choose a sequence｛Bn｝of infinite pairwise disjoint subsets of N. For an arbitrary index n∈N，we find a sequence xn∈ℓ∝possessing at least a countable set of limit points and satisfying suppxn⊆Bn.It remains to observe the validity of the relations Y0∩Lin｛x1，x2，···｝=｛0｝and dimLin｛x1，x2，···｝=∞.On the other hand，it is not clear if the assumption of the closedness of the range R（T）in the second part of the preceding theorem is important.The condition of the closedness may be rejected if the equality codimR（T）=∞implies codimFor some classes of operators on ℓ∝，this implication is true（see Corollary 2.19）.Below，we will prove the following assertion：

（A）For every operator T on ℓ∝satisfying codimR（T）=∞，we have codimif and only if for every operator T on ℓ∝satisfying，we have R（T）=ℓ∝.

Unfortunately，the author does not know an example of an operator T on the space ℓ∝such that the relationholds while R（T）6=ℓ∝.Moreover，it is not known if，under the assumptions of Theorem 2.10，more can be asserted，namely，the validity of the relation R（T）∩Lin｛χA1，χA2，···｝=｛0｝or at least that for every k，there exist nonempty pairwise disjoint subsets B1，···，Bk⊆N satisfying R（T）∩Lin｛χB1，···，χBk｝=｛0｝（this must hold ifthe identity u（T）=d（T）is true）.

Let us verify the assertion（A）.Only the sufficiency needs a proof.Consider an operator T on ℓ∝satisfying the relation codimR（T）=∞.Proceeding by contradiction，we find a finitedimensional space L with dimL=m such thatbe a basis in L and let Q be an operator on ℓ∝defined via the formula Qx=（xm+1，xm+2，···）.Next，define the operator S on ℓ∝via the formula.The identity

holds.To see this，we consider an element x∈R（T）⊕L and find an element z∈ℓ∝and scalars λ1，···，λmsatisfyingFor the sequence y=（λ1，···，λm，z1，z2，···）∈ℓ∝，we have Sy=x，whence x∈R（S）and（2.7）has been proved.This implies easily the equalityAccording to our condition，we get R（S）=ℓ∝.Taking into account（2.7）once more，we infer codimR（T）＜∞，a contradiction.

Before proceeding further，we introduce the following two notions which will be needed later.To this end，let｛an｝be a sequence in a topological space A equipped with a topology τ. Define the subset A0of A by A0=｛a1，a2，···｝.

Definition 2.11We call an0an isolated element of the sequence｛an｝（in the topology τ）if there is a neighborhood U of the point an0with an/∈U for all n 6=n0.

Obviously，every accumulation point an0of the set A0is not an isolated element of｛an｝.

Definition 2.12We will define the defect δ｛an｝of the sequence｛an｝in the following manner.If the set of unisolated elements of｛an｝is infinite，then we put δ｛an｝=∞and if it is empty，then we put δ｛an｝=0.Otherwisebe unisolated elements of the sequence｛an｝which are also accumulation points of the set A0and letthe rest of unisolated elements of｛an｝，moreovermention that for every index i∈｛k′+1，···，k｝，there exists an indexwith the property ani=anj.Consequently，either k′=k，that is，all unisolated elements of｛an｝are accumulation points of A0or k−k′＞card，where，of course，is the cardinality of the setthat is，the number of different points amongstNow，we put δ｛an｝=

Evidently，the equality δ｛an｝=0 holds if and only if all elements of the sequence｛an｝are isolated.If the defect δ｛an｝∈N，then it is equal to the least number of elements of the sequence｛an｝such that deleting these elements from｛an｝，we obtain the sequence of defect zero.For example，the defect of the sequencein N or in R is equalin R is equal to m，and the defect of to m−1，the defectin R is also equal to m.If｛tn｝is an arbitrary sequence in βN，then the identityholds（here，and further，the sequenceis considered in the spacewith theIn some cases，it turns out that using the notion of defect of a sequence，the defect d（T）of an operator T on ℓ∝can be calculated（see Theorem 2.17（b）and Corollary 2.18 below；in particular，the identity（2.17））.

In the next theorem，geometric properties of lower semi-Fredholm sequences are collected.

（a）For some index n0，the elements，···are linearly independent and，in particular，for all n，m≥n0，n 6=m；

（c）The number of unisolated elements of the sequence｛｝in the σ（）-topology is finite，that is，δ｛x∗n｝＜∞.

ProofThe assertions（a）and（b）follow from the relation｛｝～｛｝（see Remark 2.5（b））.Nevertheless，part（a）and the assertion that the sequence｛｝does not have norm convergent subsequences admit a simple proof.Actually，if（a）is not valid，then we can choose

indices m1＜m2＜···and scalars λm2k−1，···，λm2k，not all zero，satisfyingfor all k.Then，

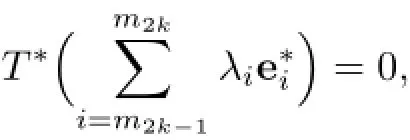
where T is the operator defined by｛，which is a contradiction with the relation n（T∗）＜∞. Next，assume that some subsequence.Define a sequence｛｝by=if n∈｛n1，n2，···｝and=0 otherwise and consider a compact operator K defined by this sequence.Then，R（T−K）∩Lin｛en1，en2，···｝=｛0｝.We arrive at a contradiction with the relation T−K∈Φ−（ℓ∝）.

（c）We will show the validity of the inequality δ｛x∗n｝≤u（T）which，by Corollary 2.8，implies the required assertion.Let，···be a system of unisolated elements of the sequence｛x∗n｝such that ri6=rjfor i

belong to the σ）-closure of the set｛xn：n∈/｛r1，···，rp｝｝，the system（A1，···，Ap）is T-inaccessible and，hence，p≤u（T）.Now，the desired inequality is clear.

The converse statement to the preceding theorem is not valid，that is，a bounded sequenceinsatisfying conditions（a）-（c）of Theorem 2.13 need not be lower semi-Fredholm. Actually，for the check of it，it suffices to consider the sequence｛｝of Example 2.9（a）；we also mention the validity，in this case，of the identity δ｛｝=0.As will be shown below（see Corollary 2.18），in some cases the condition（c）of Theorem 2.13，that is，the inequality，＜∞，implies thatis lower semi-Fredholm.

2.2The case of an almost diagonal operator T

Definition 2.14An operator T onis said to be almost diagonal if it is defined by a sequence｛｝，where｛｝and｛｝are sequences in R and in βN，respectively，and｛dn｝is bounded；in this case，we have

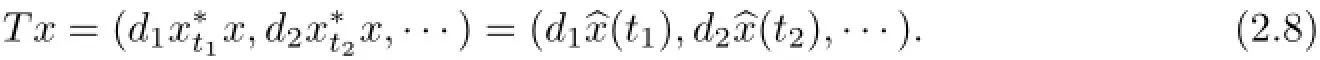
If tn=n for all n∈N，then

is a“usual”diagonal operator.Next，an operator T on ℓ∝defined by a sequence｛｝inis said to be generalized diagonal if every element x∗of the span of the set｛，···｝can be represented in the form of a linear combination of some pairwise disjoint elementsthat is，

Evidently，every almost diagonal operator is generalized diagonal.

In the next theorem，the conditions are given which imply the closedness of the range of a generalized diagonal operator.Before stating it，we mention the following assertion：For Banach spaces X and Y and an operator S∈L（X，Y），the range R（S）is（norm）closed if and only if the range R（S∗）is σ（X∗，X）-closed.Indeed，if R（S）is closed，then［1，p.79，Exercise 12（a）］the identity

holds.The latter at once implies the σ（X∗，X）-closedness of R（S∗）.For the converse，if R（S∗）is σ（X∗，X）-closed，then it is closed.By Banach's theorem［1，p.76］，R（S）is also closed.

Theorem 2.15Let T be a generalized diagonal operator on ℓ∝defined by a sequence｛x∗n｝in ℓ∗∝such that either card｛n：x∗n6=0｝＜∞or

（a）The equality

holds，where the closure was taken in the σ（ℓ∗∝，ℓ∝）-topology and BL=Bℓ∗∝∩L；

（b）For some δ＞0 and all x∈ℓ∝，the inequalityholds；

（c）T is an almost diagonal operator.

（a）In view of the remarks above，it suffices to check the equality R（T∗）=L.Moreover，using relation（2.10），it is easy to see that we can assume the validity of the inequality‖for all n and some δ1＞0.Asand the subspace Lin｛，···｝is σ（）-dense in，the inclusion R（T∗）⊆L is clear.To establish the converse inclusion，consider a functional z∗∈L.There exists a net｛｝in L satisfyingBy equality（2.11），we can assume the boundedness of｛｝.For an arbitrary index α，we find scalarsand functionalssuch thatWe can suppose that the functionalsare pairwise disjoint.Using the latter，we have

（b）It suffices to show the inclusion，which at once implies（2.11）and，moreover， the identity L=（In fact，from the ideal convexity of the setit follows［10，pp.10，11］that the validity of the last inclusion for some δ＞0 is equivalent to equality（2.11）with=）.Let a functionalBy the classical Separation Theorem［5，p.136］，there exist an element x∈ℓ∝and a number ǫ＞0 satisfying l∗x+ǫ≤x∗x for allUsing our condition，we obtain，a contradiction（the given argument is true for every subspace L of the dual Z∗of some Banach space Z）.

（c）Let T be an operator defined by a sequencewith dn∈R and tn∈βN. Again we will check（2.11）.First of all，we note that the subspace L is an ideal in ℓ∗∝because the functionalsare atoms of the Banach lattice.Consequently，the subspace L◦◦，where the polars are taken in the Riesz dual systemis a band inOn the other hand，by the Bipolar Theorem［5，p.140］，Now，letWe will check thatfor some real k＞0.By the remarks above，we can assumeThe inclusion

holds.In fact，if there is a point t∈suppµz∗｛t1，t2，···｝βN，then，applying Urysohn's lemma［9，p.44］，we find z∈ℓ∝satisfyingfor all n. ThusIn contrast，there exists a net｛｝in L such thatwhence 0=or z∗|z|=0.This is a contradiction and（2.12）has been proved.Now，we will show the inclusion，where L+=｛l∗∈L：l∗≥0｝.Indeed，ifthen，using the classical Separation Theorem once more，we find x∈ℓ∝and ǫ＞0 satisfying l∗x+ǫ≤z∗x for all l∗∈L+.Hence，l∗x≤0 for l∗∈L+.Therefore，b x（tn）≤0 for all n and z∗x＞0.The latter inequalities contradict（2.12）.Thus，z∗∈Consequently，there exists a net｛｝in L+such that，in particular，Therefore，we can assume the boundedness of｛｝.Finally， z∗

The conditions（2.10）and（2.11）do not imply the closedness of the range R（T）of an arbitrary operator T on ℓ∝.For instance，consider the sequence｛｝infrom Example 2.9（a）and the operator T on ℓ∝defined by｛x∗n｝，that is，Tx=（x1，x2−x1，x3−x2，···）.Obviously，Next，it is easy to see that equality（2.11）holds with L=andHowever，the subspace bs is not closed in ℓ∝.Indeed，the sequence

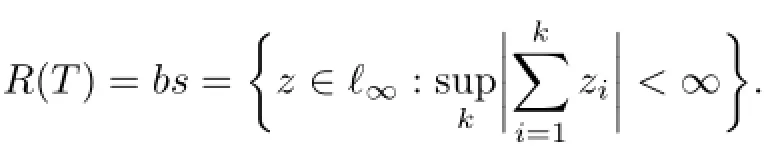
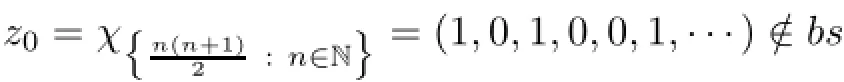
while（see，for example，［4］）z0∈bs.In contrast，it is not known if the range R（T）of an arbitrary generalized diagonal operator T defined by a sequence｛｝satisfying（2.10）is closed even when elements of｛｝are pairwise disjoint.In this case，the answer is affirmative if∈ℓ1. Moreover，the author does not known an example of a subspace L of the spacefor which（2.11）does not hold.It should be mentioned that there exist a Banach space Z which is even an AM-space and a subspace L0of the dual Z∗which is σ（Z∗，Z）-dense in Z∗while Z∗6=We also note that an almost diagonal operator may not be both lower and upper semi-Fredholm even when（2.10）holds（see Example 2.20（d）below）.

Before than we turn our attention to the study of Fredholm properties of almost diagonal operators，the following lemma will be proved.

Lemma 2.16Let X，Y，and Z be three Banach spaces and let T∈L（X，Y）and S∈L（Y，Z）.The following statements hold：

（a）If d（T）＜∞，S∈Φ（Y，Z），and N（S）∩R（T）=｛0｝，then d（ST）=d（T）−indS；

（b）If d（T）=∞and n（S）＜∞，then d（ST）=∞.

Proof（a）First of all，recall that the index of an arbitrary operator S0∈Φ（Y，Z）is the number indS0=n（S0）−d（S0）.Consider the quotient vector space X/N（T）and define an operatorbT from X/N（T）into Y via the formulabT（x+N（T））=Tx for x∈X.Obviously，bT is well defined，R（T）=R（bT），and N（bT）=｛0｝.Consequently，bT∈Φ（X/N（T），Y）and，hence，SbT∈Φ（X/N（T），Z）and indbT=−d（T）.We have the relations

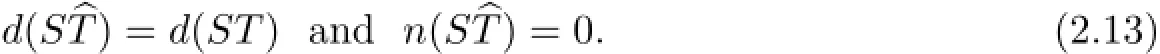
The former at once follows from the equality R（ST）=R（SbT）and implies d（ST）＜∞if the assumptions d（T）＜∞and S∈Φ（Y，Z）only hold.We will check the second.If SbT（x+N（T））= 0，then Tx=bT（x+N（T））∈N（S）.Whence，using our conditions，we conclude Tx=0，that is，x+N（T）=0，as desired.Now，taking a glance at（2.13），we obtain the relation ind（SbT）=−d（ST）.In contrast，by the Index Theorem［1，p.158］，we get

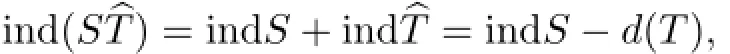
and（a）has been established.

（b）Proceeding by contradiction，we assume that d（ST）＜∞.There exist a subspace L of the space Y satisfying R（T）⊕L=Y and dimL=∞and a subspace M of the space Z satisfying R（ST）⊕M=Z and dimM=d（ST）.Put m0=dimM.For an arbitrary number k∈N，we choose k（m0+1）linearly independent elements lijof L with 1≤i≤k and 1≤j≤m0+1. Evidently，Slij=STxij+mijfor some xij∈X and mij∈M.As elements mi1，···，mi，m0+1are linearly dependent for an arbitrary index i，there are scalars λi1，···，λi，m0+1，not all zero，satisfying

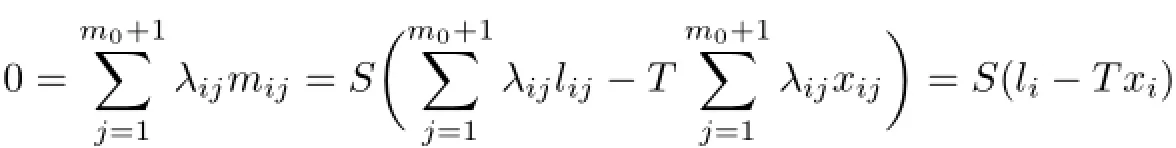
Theorem 2.17Let｛tn｝be a sequence in βN and let｛dn｝be a bounded sequence in R. Then，for an almost diagonal operator T on ℓ∝of the form（2.8），the next assertions hold：

（a）The condition

for some δ1＞0 is sufficient and，if one of two following assumptions（i）or（ii）holds，is necessary for the closedness of the range R（T）：

（i）For all k∈N，the inequality card｛m：tm=tk｝＜∞is valid and there exist a number R＞0 and，for all sufficiently large n，a neighborhood Vnof the point tnsuch that the inclusion tm∈Vnfor some index m implies|dm|≤R|dn|；

（ii）For all sufficiently large n，every element tnis an isolated element of the sequence｛tn｝；

（b）If relation（2.14）holds for some δ1＞0，then

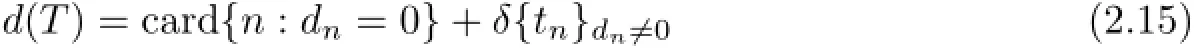
and，in particular，if

for some δ2＞0，then we have the identity

（c）If relation（2.14）does not hold for every δ1＞0，then d（T）=∞；

（d）The defect d（T）satisfies the identity

Proof（a）The closedness of R（T）follows from Theorem 2.15（c）.Below we suggest a simpler way to prove it.To this end，let（2.14）hold and let the relation Txk→z be valid for some sequence｛xk｝in the space ℓ∝and an elementuniformly in n.Hence，uniformly on the set｛n：dn6=0｝.The latter follows at once from the inequalityThen，T is compact and the sequence︿xkis a Cauchy sequence in the space C（T）.Consequently，for some f0∈C（T），we haveObviously，

for all n satisfying dn6=0.By Urysohn Extension Theorem［9，p.43］，the function f0can be extended to a continuous function f in C（βN）.Then，for some element x∈ℓ∝，we have b x=f. Hence，applying（2.19），we get zn=dnb x（tn）if dn6=0.Evidently，this relation is also valid if dn=0.Finally，Tx=z，that is，R（T）is closed.

Now，let R（T）be closed and let the condition（i）hold，in particular，in view of the first part of it，there are no elements of the sequence｛tn｝repeating infinitely many times in it.Proceeding by contradiction，we find a subsequence｛dnk｝of｛dn｝satisfying dnk→0 as k→∞and dnk6=0for all k.Consider the sequence｛tnk｝.Since in βN，as in every extremally disconnected space，there exist no non-trivial convergent sequences，we find an open-and-closed neighborhood U1of the point tn1satisfying card｛ni：tni/∈U1｝=∞.By passing to a subsequence if needed，we can assume that tni/∈U1for all i＞1.There exists an open-and-closed neighborhood U2of the point tn2satisfying U1∩U2=∅and card｛ni：tni/∈U2｝=∞.Again we assume tni/∈U2for all i 6=2 and find an open-and-closed neighborhood U3of the point tn3satisfying（U1∪U2）∩U3=∅and card｛ni：tni/∈U3｝=∞.Iterating this procedure，as a result，we can assume that there is a sequence｛Uk｝of open pairwise disjoint subsets of βN with the property tnk∈Ukfor all k. Define the sets Ak=｛m∈N：tm∈Uk｝.Considering the second part of（i），we can suppose the validity of the inequality

for all m∈Ak.By Urysohn's lemma［9，p.44］，there exists a sequence｛yk｝in ℓ∝such that=1，=｛0｝，and‖yk‖≤1 for all k，in particular， ybk（tni）=0 for i 6=k. Clearly，suppTyk⊆Akand suppTyi∩suppTyj=∅for i 6=j.Using inequality（2.20），we have≤R|dnk|for all m∈Akand，hence，‖Tyk‖≤R|dnk|.Consequently，the sequenceis bounded and belongs to R（T）.Next，by the closedness of R（T），for

every real sequence｛αi｝converging to zero，the element In particular，for

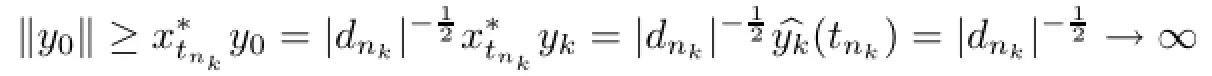
as k→∞，a contradiction.

In the case of（ii），for sufficiently large n，we find a neighborhood Vnof the point tnsatisfying tk∈/Vnfor k 6=n.Now，it remains to observe that the condition（i）holds with R=1.

（b）If card｛n：dn=0｝=∞，then d（T）=∞and，hence，identity（2.15）is valid.

Now，let card｛n：dn=0｝＜∞.In this case，the sequenceobtained from the sequence｛tn｝by the deletion of elements tnwith dn=0 is well defined.First of all，we will show that（2.16）implies（2.17）.

To this end，let（2.16）hold.We consider three cases.

The case of δ｛tn｝=0.For an arbitrary sequence，we define the function g0on the set T0=｛t1，t2，···｝via the formulaAs every element of the sequence｛tn｝is isolated，the function g0is well defined and continuous on the countable subset T0of the space βN.Moreover，by the inequality，function g0is bounded.Consequently［9，p.97，Exercise 6O.6］，g0can be extended to a continuous function g in C（βN）.There exists an element x∈ℓ∝such that xb=g and，hence，or Tx=z.Finally，R（T）=ℓ∝or d（T）=0.

The case of 0＜δ｛tn｝＜∞.Let tn1，···，tnmbe a system consisting of all unisolated elements of the sequence｛tn｝with n1＜···＜nm.Define the operator S1on ℓ∝by

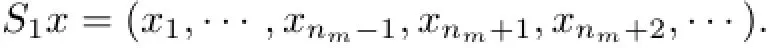
Obviously，S1∈Φ（ℓ∝），indS1=1，and N（S1）=｛λenm：λ∈R｝.As tnmis an unisolated elements of｛tn｝，the relation N（S1）∩R（T）=｛0｝holds.Then，using Lemma 2.16，we getd（S1T）=d（T）−1（if d（T）=∞，then d（S1T）=∞）.The operator S1T is defined by the sequence

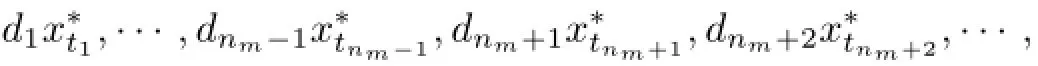
moreover，the system of unisolated elements of the sequence

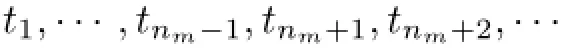
is either（I）the system tn1，···，tnm−1or（II）if tnmis not an accumulation point of the set｛t1，t2，···｝and there exists a unique index nj∈｛n1，···，nm−1｝such that tnj=tnm，the system tn1，···，tnj−1，tnj+1，···，tnm−1（if j=m−1，then this is the system tn1，···，tnm−2）. Define the operator S2on ℓ∝by

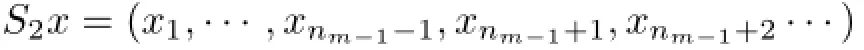
（if（II）holds and j=m−1，then

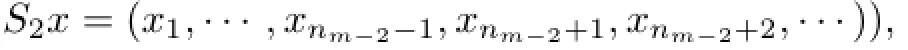
that is，S2is built for the operator S1T and for the system of unisolated elements corresponding to it.We get d（S2S1T）=d（S1T）−1=d（T）−2.For the operator S2S1T and its system of unisolated elements，we build the operator S3，and so on.As a result，a situation which is analogous to（II），that is，when from the system of unisolated elements of the operator Si···S1T after it multiplying by Si+1two elements are deleted but not one，holds exactly so many times which is the cardinality of the set of unisolated elements of the sequence｛tn｝not being accumulation points of｛t1，t2，···｝.Thus，taking δ｛tn｝steps，we obtain the operator Sδ｛tn｝···S1T which satisfies the relation d（Sδ｛tn｝···S1T）=d（T）−δ｛tn｝and is defined by the sequence

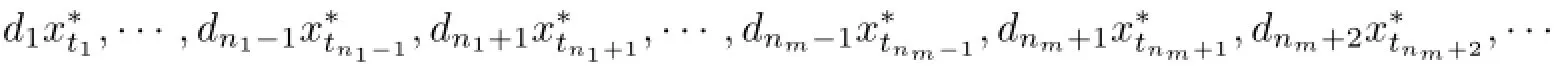
such that the sequence

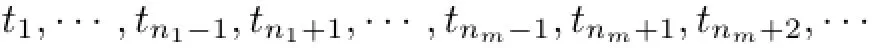
does not have unisolated elements.As was shown above，d···S1T）=0，and，hence，d（T）=δ｛tn｝.

The case of δ｛tn｝=∞.Consider two operators D and T0on ℓ∝defined by the sequences｛and｛｝，respectively.Using the equalities δ｛｝=δ｛tn｝=∞and Theorem 2.13（c），we have d（T0）=∞.Whence，by the relations DT0=T and n（D）=0 and Lemma 2.16（b），we get d（T）=∞.The proof of identity（2.17）is finished.

Next，let（2.14）hold and let｛n：dn=0｝=｛n1，···nk｝6=∅with n1＜···＜nk.For i=1，···，k，we define operatorsonby

（c）Assume that relation（2.14）does not hold for every δ1＞0.Then，there exists a subsequence｛dnk｝of｛dn｝satisfying dnk→0 as k→∞and dnk6=0 for all k.The former implies thecompactness of the operator PBT，where the set B=｛dn1，dn2，···｝.Now，if d（T）＜∞，that is，T∈Φ−（ℓ∝），then T−PBT∈Φ−（ℓ∝），which is impossible（see，for example，Theorem 2.13（a））.

（d）Assume first that relation（2.14）does not hold for every δ1＞0.Again there exists a subsequence｛dnk｝of｛dn｝satisfying dnk→0 as k→∞and dnk6=0 for all k.Fix p∈N. Let A1，···，Apbe some partition of the set｛n1，n2，···｝to infinite pairwise disjoint subsets.

Then，the system（A1，···，Ap）is T-inaccessible and，hence，u（T）≥p.As p is arbitrary，we have u（T）=∞.By part（c），d（T）=∞，as required.

Now，assume that relation（2.14）holds.If card｛n：dn=0｝=∞，then u（T）=d（T）=∞. Let k=card｛n：dn=0｝∈N∪｛0｝.If k＞0，then we can find indices n1，···，nksatisfying dni=0 for i=1，···，k.Next，let tnk+1，···，tnk+m′be some collection of accumulation points of the set｛tn：dn6=0｝and let tnk+m′+1，···，tnk+mbe some collection of unisolated points of the sequence｛tn｝dn/=0such that m′≤m，ni6=njfor i 6=j and i，j=1，···，k+m，and for every index∈｛nk+m′+1，···，nk+m｝，there exists an index n′0′∈/｛n1，···，nk+m｝satisfying

tn′0

=tn′0′.For i=1，···，k+m，we define the sets Ai=｛ni｝.It is easy to check that the system（A1，···，Ak+m）is T-inaccessible and，hence，u（T）≥k+m.In view of an arbitrary choice of elements tnk+1，···，tnk+m，we have u（T）≥k+δ｛tn｝dn/=0.Whence，using Proposition 2.7（c）and identity（2.15）above，we obtain d（T）≥u（T）≥k+δ｛tn｝dn/=0=d（T）.Finally，u（T）=d（T）. The proof of the theorem is now completed.

Corollary 2.18Let｛tn｝be a sequence in βN and let T be an operator on ℓ∝defined by the sequence｛x∗tn｝.Then，the range R（T）is closed and d（T）=δ｛tn｝=δ｛x∗tn｝.

ProofProceeding by contradiction，we assume that codimTherefore，there is a finite-dimensional space L with dimL=m satisfyingand the range R（T）is not closed.Whence，by Theorem 2.17（a），there exists a subsequence｛dnk｝of｛dn｝satisfying dnk→0 as k→∞and dnk6=0 for all k.Let A1，···，Am+1be an arbitrary partition of the set｛n1，n2，···｝to infinite pairwise disjoint subsets.For every i=1，···，m+1，we findand li∈L such that χAi=yi+li.As the elements l1，···，lm+1are linearly dependent，for some scalars λ1，···，λm+1，not all zero，the identity=0 holds and，hence，

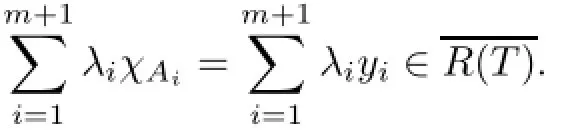
Example 2.20（a）Let T be a diagonal operator on ℓ∝defined by relation（2.9）.Obviously，the condition（ii）of Theorem 2.17（a）holds.Therefore，R（T）is closed if and only if（2.14）is valid for some δ1＞0.In contrast，applying part（b）of the same theorem，it follows T∈Φ−（ℓ∝）if and only if card｛n：dn=0｝＜∞and（2.14）is valid；this is also equivalent（see Theorem 2.13（b））to the fact that the sequencedoes not have a weakly convergent subsequence.

（b）In general case，the closedness of R（T）does not imply the condition（2.14）.Actually，let｛sn｝and｛dn｝be two arbitrary sequences in βN and R，respectively，and let d2n−1=1 and d2n6=0 for all n and d2n→0 as n→∞.Define the sequences｛tn｝in βN and｛｝invia the formulae t2n=snand t2n−1=n for all n and=dnx∗tn.Consider the operator T onℓ∝defined by｛x∗n｝，that is，Tx=···）.Clearly，for the operator T the condition（2.14）does not hold.Nevertheless，the range R（T）is closed（it is easy to see directly that conditions（i）and（ii）of Theorem 2.17（a）do not hold in this case）.

We will show more，namely，let｛zn∗｝be an arbitrary Fredholm sequence defining the operator S on ℓ∝with the property n（S）=0 and let｛nk｝be a subsequence of the sequence of the natural numbers.Consider，in addition，an arbitrary bounded sequence｛｝insatisfying=for all k.Let T0be the operator defined by｛；if S=I，nk=2k−1，and=then T0=T.We claim that R（T0）is closed.Indeed，define the sequence｛u∗n｝invia the formulae u=for n∈｛n1，n2，···｝and=0 otherwise.Let U be the operator on ℓ∝defined by｛.If for a sequence｛xk｝in ℓ∝，the sequence｛T0xk｝converges，then｛Uxk｝and，hence，｛Sxk｝，also converges.As N（S）=｛0｝and R（S）is closed，｛xk｝is also convergent.Now，the closedness of R（T0）is obvious.

For the operator T constructed in this example，one may take the sequence｛tn｝to be such that ti6=tjfor i 6=j.It is easy to construct a counterexample that need not satisfy this condition.For example，take the rank-one operator T1defined by T1x=⊗d）x=，···）with t∈βN and d∈c0.

（c）In this part，we make a number of remarks about a connection between δ｛tn｝and δ｛x∗n｝，where=and a sequence｛is considered inwith the σ）-topology（we use the notations of Theorem 2.17）.First of all，we mention that if dn→0，then the operator T is compact.Hence，if dimR（T）=∞，then R（T）is not closed.Consequently，d（T）=∞，but，of course，δ｛tn｝＜∞and δ｛tn｝=0 are even possible.If dn=1−，then‖‖=1−whence δ｛｝=0，but，in this case，a value δ｛tn｝can be any（see，in particular，part（d）below）.In contrast，δ｛≥card｛n：dn=0｝−1，in particular，if card｛n：dn=0｝=∞，then δ｛｝=∞.If card｛n：dn6=0｝=∞，then the following inequality

∈0

Now，by the relations

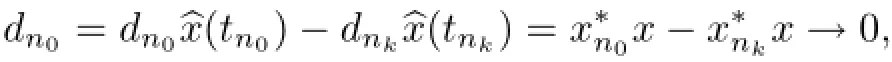
we infer dn0=0，a contradiction.As a result，tn0is an accumulation point of｛t1，t2，···｝. Therefore，ifis an unisolated elements of the sequence｛，then tn0is also an unisolated element of｛tn｝.Now，（2.21）is clear.It follows at once from（2.21）that if dn6=0 for all n，then δ｛tn｝≥δ｛｝.

（d）A sequence｛tn｝in βN with the properties

can be constructed in the following manner.Let N1，N2，···be an arbitrary partition of the set N to infinite pairwise disjoint subsets.Thenfor i 6=j andis an open set for all i.For every index i，we choose a sequencesuch that sij′6=sij′for j′6=j′′.Let sibe a cluster point of this sequence.EvidentlyEnumerating by an arbitrary manner the set S=｛sij，si：i，j∈N｝，we obtain a sequence｛tn｝satisfying the conditions（2.22）.If S⊆βNN，then it is well known that（c0）=｛0｝for all n，that is，for the operator T defined by the sequence｛x∗tn｝，the relation T（c0）=｛0｝holds，whence T∈/Φ−（ℓ∝）∪Φ+（ℓ∝）or，in other words，｛｝is not neither lower nor upper semi-Fredholm. In contrast，if the inclusion N⊆S is valid（it can always be obtained by a corresponding choice of sij），then｛｝is upper semi-Fredholm and not lower semi-Fredholm.Now，if we put tn=sn，then｛｝is lower semi-Fredholm and not upper semi-Fredholm.In all these cases，｛｝does not have a weakly cluster point as a sequence of pairwise disjoint elements in an AL-space

3　Conditions that T∈Φ+（ℓ∞）

The purpose of this section is to discuss conditions under which an operator T defined by a sequence｛｝inis upper semi-Fredholm.As the conditions of the closedness of the range R（T）were considered in the preceding section，we will limit ourselves by the study of the conditions of n（T）＜∞.

Theorem 3.1Let T be an operator on ℓ∝defined by a sequenceand let L be the（norm）closure of Lin｛，···｝.Then，n（T）＜∞if and only if there exists a finite dimensional subspace Y of ℓ∗∝such that L∩Y=｛0｝and the space L+Y separates ℓ∝.

ProofFirst，we shall prove the necessity.If n（T）=0，then obviously we can take Y=｛0｝.Let n（T）＞0.There exist elements z1，···，∈N（T）and functionals，···∈ℓ∗∝satisfying the relation，where δijis the Kronecker delta.Put

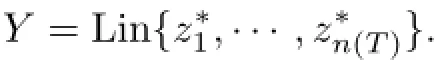
If y∗∈L∩Y，then，with αi∈R.Whence for all j=1，···，n（T），we have 0=y∗zj=αj，that is，y∗=0 or L∩Y=｛0｝.Next，if for an element x∈ℓ∝，the equalities=0 with n∈N andx=0 with i=1，···，n（T）hold，then from the first one，we obtain x∈N（T）or x=with βj∈R and now from the second，wehave 0=z∗ix=βi，that is，x=0.

For the converse，define the operator S：N（T）→Y∗as follows.For an element x∈N（T）and a functional y∗∈Y，we put（Sx）y∗=y∗x，then operator S is one-to-one.Indeed，if Sx=0，then y∗x=0 for all y∗∈Y and，hence，by x∈N（T），we conclude z∗x=0 for all z∗∈L+Y.Therefore，x=0.Finally，n（T）≤dimY∗=dimY＜∞.

Example 2.20′Let T be a diagonal operator on ℓ∝defined by relation（2.9）.It is easy to see that n（T）=card｛n：dn=0｝.Consequently（see Example 2.20（a）），T∈Φ+（ℓ∝）if and only if card｛n：dn=0｝＜∞and（2.14）is valid for some δ1＞0；in particular，T∈Φ+（ℓ∝）if and only if T∈Φ−（ℓ∝）and this is also equivalent to the condition T∈Φ（ℓ∝）.

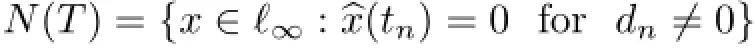
In the case of an almost diagonal operator of form（2.8），the relation holds obviously.Nevertheless，for such operators，the condition T∈Φ−（ℓ∝）does not imply T∈Φ+（ℓ∝）and vice versa（see Example 2.20（d））.

It is well known that an operator T：X→Y between two Banach spaces is upper semi-Fredholm if and only if given any bounded set M⊆X which is not relatively compact，it is true that T（M）is also not relatively compact（see［7，p.8，Theorem 1.3.2］，where this result was proved in the case of X=Y，while in the general case the proof of it is analogous）.Finally，we close this section by presenting the next result in this direction（see Theorem 2.13 in this connection）.

Proposition 3.2Let X and Y be Banach spaces and let T be an operator from X into Y such that N（T）is reflexive and complemented and R（T）is closed（for example，T is upper semi-Fredholm）.If M is bounded and weakly closed subset of X，then the image T（M）also has this properties；in addition，if M is discrete in the topology induced by the weak topology，then T（M）is likewise discrete.

ProofLet M⊆X be bounded and weakly closed.It is enough to verify the weak closedness of the set T（M）.The space X can be represented in the form of the direct sum X=N（T）⊕W，where W is a closed subspace of X.The restriction TWof the operator T to W is an isomorphism between W and R（T）.Let P：X→X be the projector satisfying R（P）=W and N（P）=N（T）.Obviously，T（M）=TWP（M）.Thus，it suffices to check the weak closedness of P（M）and，consequently，it suffices to prove the required assertion under the assumption that T on X is a projector.

To this end，let T be a projector and let a net｛mα｝α∈Jin M and an element x∈X exist， satisfying. As N（T）is reflexive，a net｛（I−T）mα｝has a weakly cluster point z∈N（T）.The inclusion x+z∈M holds.Indeed，it suffices to show that x+z belongs to the weak closure of the set｛mα：α∈J｝.To see this，fix an arbitrary σ（X，X∗）-neighborhood U of zero and consider another σ（X，X∗）-neighborhood V of zero satisfying V+V⊆U.Choose an index α0for which Tmα−x∈V for all α≥α0.Find an index α′≥α0for which（I−T）mα′−z∈V.Then，mα′−（x+z）∈V+V⊆U.Finally，x+z∈M and，hence，

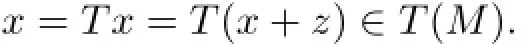
Now，let M be discrete and T be a projector on X.Proceeding by contradiction，we assume that T（M）is not weakly discrete and find an element m∈M and a net｛m′α｝α∈J′inM satisfyingTm and6=Tm for all α∈J′.Again，if z a weakly clusterpoint of｛（I−T｝，then，as was shown above，the inclusion holds.As M is weakly discrete，we have Tm+z=for some indexFinallya contradiction.

References

［1］Abramovich Y A，Aliprantis C D.An invitation to operator theory.Graduate Studies in Mathematics.Vol 50.Providence，RI，USA：American Mathematical Society，2002

［2］Aiena P.Fredholm and local spectral theory，with applications to multipliers.Dordrecht，Netherlands：Kluwer Academic Publishers，2004

［3］Alekhno E A.The lower Weyl spectrum of a positive operator.Integr Equ Oper Theory，2010，67（3）：301-326

［4］Alekhno E A.Superposition operator on the space of sequences almost converging to zero.Cent Eur J Math，2012，10（2）：619-645

［5］Aliprantis C D，Burkinshaw O.Positive Operators.Orlando，Fla，USA：Academic Press，1985

［6］Bourbaki N.Topological Vector Spaces.Berlin，Germany：Springer，1987

［7］Caradus S R，Pfaffenberger W E，Yood B.Calkin Algebras and Algebras of Operators on Banach Spaces. New York，NY，USA：Marcel Dekker，1974

［8］Drewnowski L.Some characterizations of semi-Fredholm operators.Rocz PTM，1984，24（2）：215-218

［9］Gillman L，Jerison M.Rings of Continuous Functions.Princeton，NJ，USA：Van Nostrand，1960

［10］Krasnosel’skij M A，Lifshits Je A，Sobolev A V.Positive linear systems：The method of positive operators. Berlin，Germany：Heldermann，1989

［11］Schaefer H H.Banach Lattices and Positive Operators.Berlin，Germany：Springer，1974

March 10，2014；revised July 8，2015.