ROBUST STABILIZATION OF UNCERTAIN STOCHASTIC SYSTEMS WITH TIME-VARYING DELAY AND NONLINEARITY
LI Bo-ren
(School of Computer,Dongguan University of Technology,Dongguan 523808,China)
ROBUST STABILIZATION OF UNCERTAIN STOCHASTIC SYSTEMS WITH TIME-VARYING DELAY AND NONLINEARITY
LI Bo-ren
(School of Computer,Dongguan University of Technology,Dongguan 523808,China)
In this paper,we study with robust stabilization problem of uncertain stochastic time-varying delay systems with nonlinear perturbation.Constructing a suitable Lyapunov-Krasovskii functional and employ the free weighting matrix method,in terms of the linear matrix inequality(LMI)technique,we design a memoryless state feedback controller,and obtain delay dependent robust stabilization criterion for the uncertain stochastic time-varying delay systems.A numerical example and its simulation curve are given to show that the proposed theoretical result is effective.
free-weighting matrices;nonlinear perturbation;time-varying delay;feedback control
2010 MR Subject Classification:93C10;93D09
Document code:AArticle ID:0255-7797(2016)05-0898-11
1 Introduction
The problem of the stabilization of time-delayed systems was often explored in recent years.Time delays are common in engineering processes.They frequently arose in chemical processes,in long transmission lines and in pneumatic,hydraulic and rolling mill systems. The problem of stability analysis in time-delayed systems was one of the main concerns of research into the attributes of such systems.Many works on this subject were published[1-7].Depending on the information about the size of time-delays of the systems,criteria for time-delay systems can be classified into two categories,namely,delay-independent criteria [1,2]and delay-dependent criteria[3-7].Generally speaking,for the cases of small delays ,the latter ones are less conservative than the former ones.To obtain delay-dependent conditions,many efforts were made in the literature,among which the model transformation and bounding technique for cross terms[8]were often used.However,it is well known that these two kinds of methods are the main sources of conservatism.Recently,in order to reduce the conservatism,a free-weighting matrix method was proposed in[9,10]to investigatedelay-dependent stability,in which neither model transformation nor bounding technique is involved.
In recent years,the non-fragile control problem was an attractive topic in theory analysis and practical implement,because of perturbations often appearing in the controller gain,which may result from either the actuator degradations or the requirements for readjustment of controller gains.The non-fragile control concept is how to design a feedback control that will be insensitive to some error in gains of feedback control[11].Xu et al.[12]concerned the problem s of robust non-fragile stochastic stabilization and H∞control for uncertain timedelay stochastic systems with time-varying norm-bounded parameter uncertainties in both the state and input matrices,when the delay was assumed to be constant.Zhang et al.[13]dealt with the same problem for uncertain nonlinear stochastic systems at the time-varying delay case.However,there was the restriction that time-derivative of time-varying delay must be less than one,which limits the application scope of the existing results.Wang et al.[14]dealt with the problems of non-fragile robust stochastic stabilization and robust H∞control for uncertain stochastic nonlinear single time-varying delay systems.By introducing the homogeneous domination approach to stochastic systems,Liu et al.[15]investigated a class of stochastic feedforward nonlinear systems with time-varying delay.By constructing delaypartitioning dependent Lyapunov–Krasovskii functional with reciprocally convex approach,Xia et al.[16]dealt with the problem of state robust H∞tracking control for uncertain stochastic systems with interval time-varying delay.
In this paper,our objective is to solve the problem of robust stabilization of uncertain stochastic systems with time-varying delay and nonlinearity.Parameter uncertainty in the state and input matrices,It is assumed to be norm bounded.Time delay is unknown,but in the known range changes with time.The goal of this paper is to design a memoryless state feedback controller,for all admissible parametric uncertainties,and make the closedloop system is robustly stochastically stable.The present results are derived by choosing an appropriate Lyapunov functional and by making use of free-weighting matrices method. Numerical example and its simulation curve are given to show the proposed theoretical result is effective.
NotationThrough this paper,the superscript T stands for matrix transposition;Rndenotes the n-dimensional Euclidean space,Rn×mis the set of n×m real matrices,I is the identity matrix of appropriate dimensions;the notation X>0(respectively,X≥0),for X∈Rn×nmeans that the matrix X is real positive definite(respectively,positive semidefinite);the symbol∗is used to denote the transposed elements in the symmetric positions of a matrix.Matrices,if the dimensions are not explicitly stated,are assumed to have compatible dimensions for algebraic operation.
2 System Descriptions and Preliminaries
Consider the following uncertain linear stochastic differential delay system with nonlin-ear perturbation and parameter uncertainties
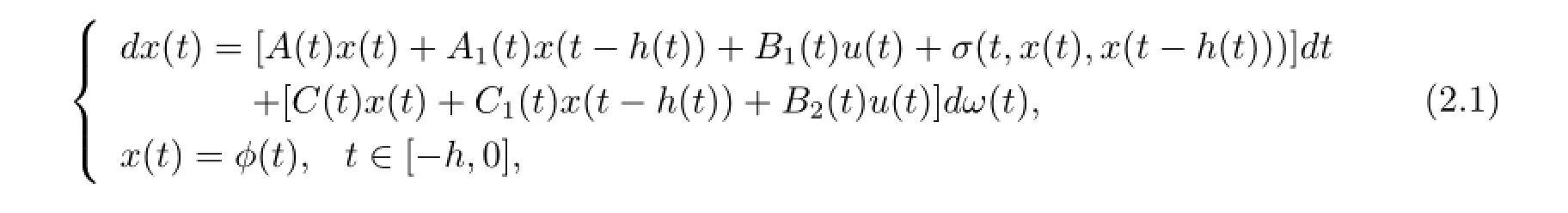
where x(t)∈Rnis the state vector,u(t)∈Rnis the control input,φ(t)is a continuoustime real valued function representing the initial condition of the system,and ω(t)is onedimensional Brownian motion defined on a complete probability space(Ω,F,P)satisfying E{dω(t)}=0,E{dω(t)2}=dt.In the system descriptive equation(2.1),the time-varying matrices are given by A(t)=A+△A(t),A1(t)=A1+△A1(t),B1(t)=B1+△B1(t),C(t)=C+△C(t),C1(t)=C1+△C1(t),and B2(t)=B2+△B2(t),where A,A1,B1,C,C1and B2are known constant matrices and△A(t),△A1(t),△B1(t),△C(t),△C1(t)and△B2(t)are unknown matrices representing time-varying parametric uncertainties in the system.They are assumed to be norm-bounded of the form
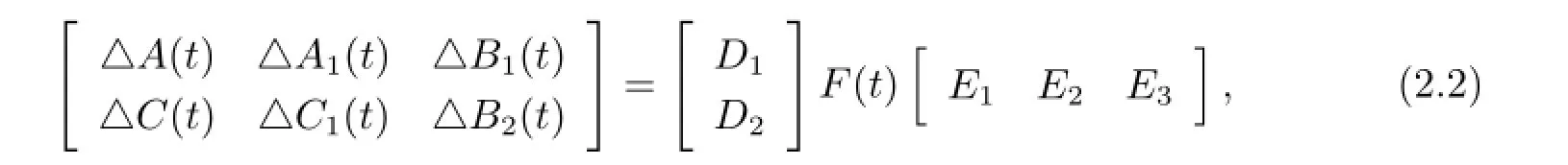
where D1,D2,E1,E2and E3are known real constant matrices with appropriate dimensions and F(t)is unknown time-varying matrix which is Lebesgue measurable satisfying FT(t)F(t)≤I,∀t.The time-varying delay h(t)is a differentiable function satisfying the following condition
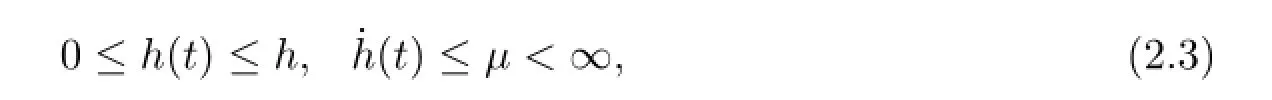
where h andµare constant scalars.The term σ(t,x(t),x(t-h(t)))∈Rnrepresents the unknown nonlinear perturbation with respect to the state x(t)and the delayed state x(th(t)),which is assumed to be bounded with the following form
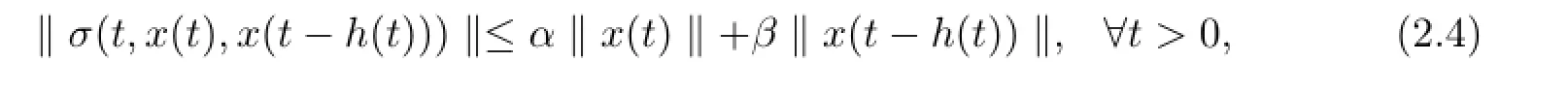
where α,β are the known non-negative constants.
Before formulating the problems to be coped with,we first introduce the following concept of robust stability for system(2.1).
Definition 1The uncertain stochastic system in(2.1)with u(t)=0 is said to be robustly stochastically stable if there exists a positive scalar†>0 such that
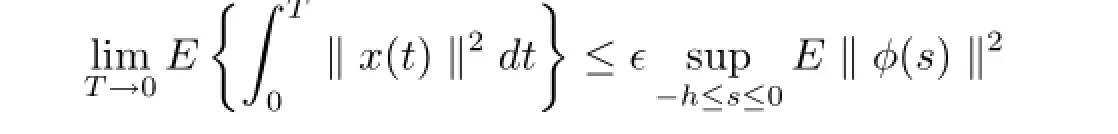
for all admissible uncertainties△A(t),△A1(t),△B1(t),△C(t),△C1(t)and△B2(t).
The objective of this paper is to develop delay-dependent stochastic stabilization criterion for the existence of a memoryless state feedback controller for system(2.1)satisfying the time-varying delay(2.3).The state feedback controller is given by

where K being the controller gain to be designed.Following lemma is indispensable for deriving the criterion.
Lemma 1For any symmetric positive-definite matrices G and Z,of appropriate dimensions,the following inequality holds
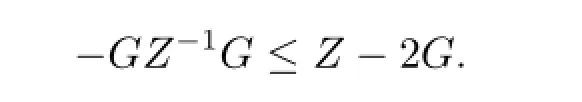
ProofSince Z>0,we have(Z-G)Z-1(Z-G)≥0.The proof follows immediately. Lemma 2[17]Given appropriately dimensioned matrices ψ,D,E with ψ=ψT.Then
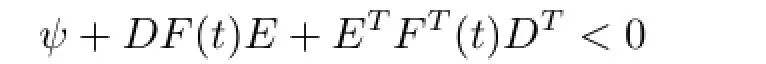
holds for all F(t)satisfying FT(t)F(t)≤I if and only if for some η>0,
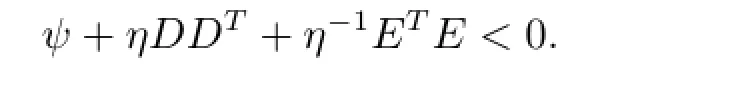
3 Main Results
Now we provide a novel delay-dependent stabilization criterion for system(2.1)as follows
Theorem 1For given positive scalars h,µand λ,if there exist symmetric positivedefinite matrices X,S1,S2,Z,appropriately dimensioned matrices Y,Uj,Vj(j=1,2,3),and positive scalars ε1,ε2,such that the following LMI hold
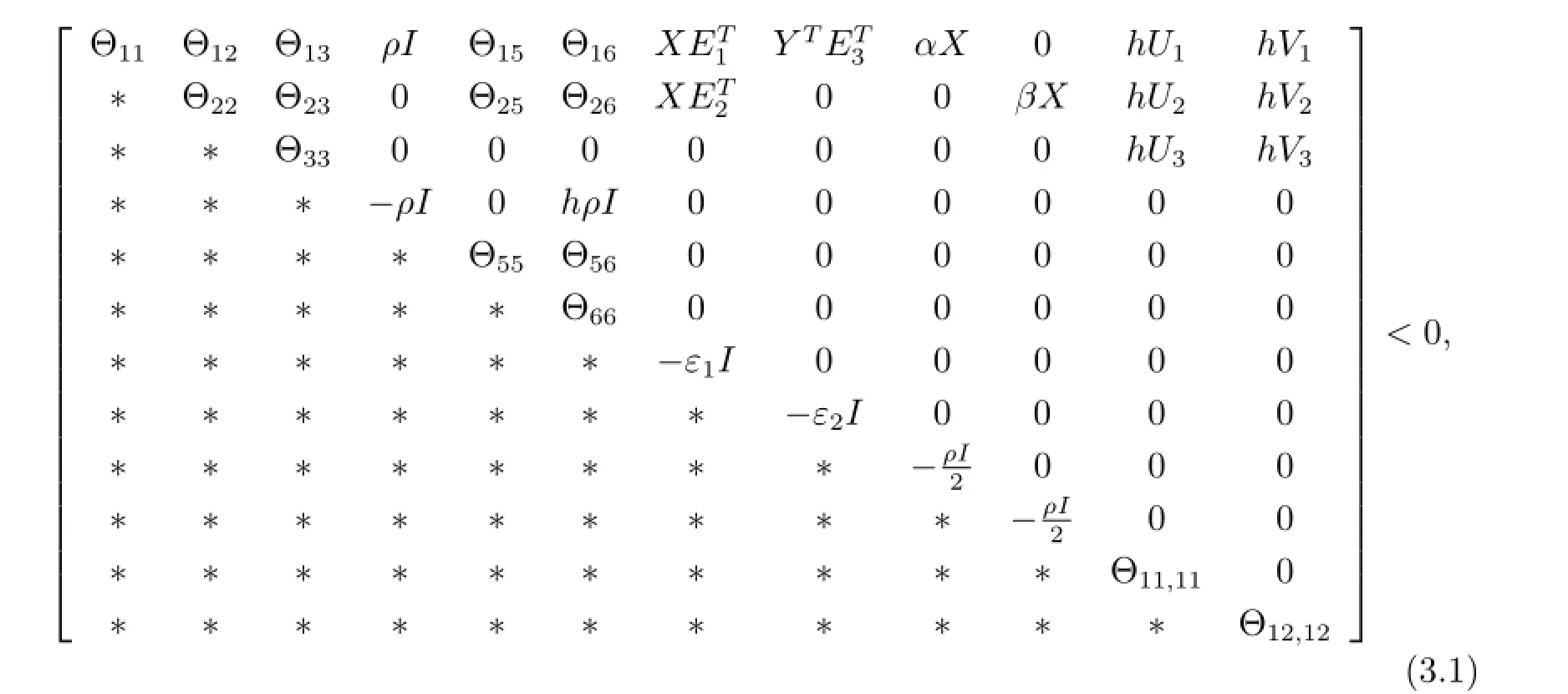
where
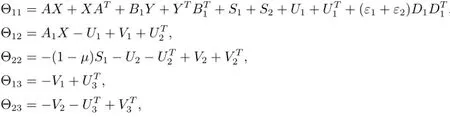
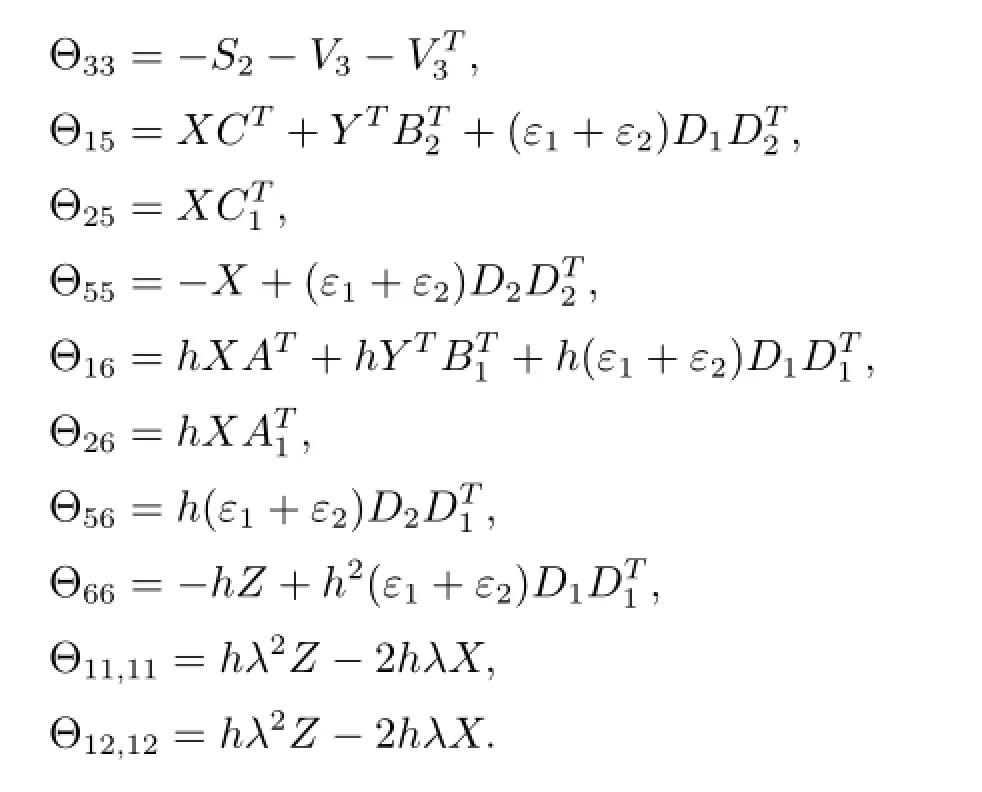
Then the uncertain linear stochastic differential delay system(2.1)with time-varying parametric uncertainties(2.2)and nonlinear perturbation(2.4)is robust stabilization,in this case,an appropriate memoryless state feedback controller can be chosen by
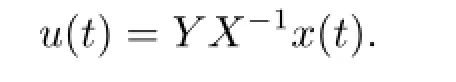
Proof Substituting the state feedback controller(2.5)into system(2.1),we obtain the resulting closed-loop system as
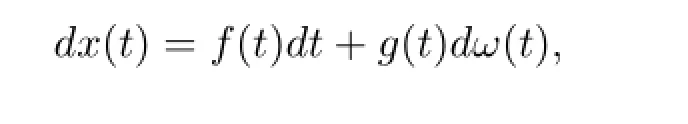
where
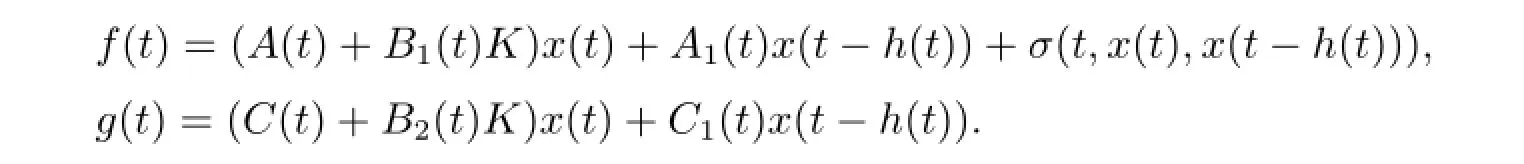
Now,choose a Lyapunov functional candidate as
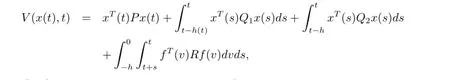
where P,Q1,Q2and R are symmetric positive-definite matrices to be chosen. By Itˆo's differential formula,we obtain stochastic differential as follows
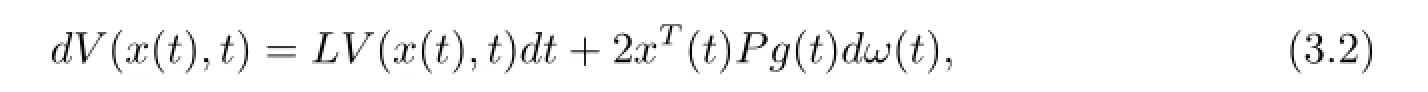
where
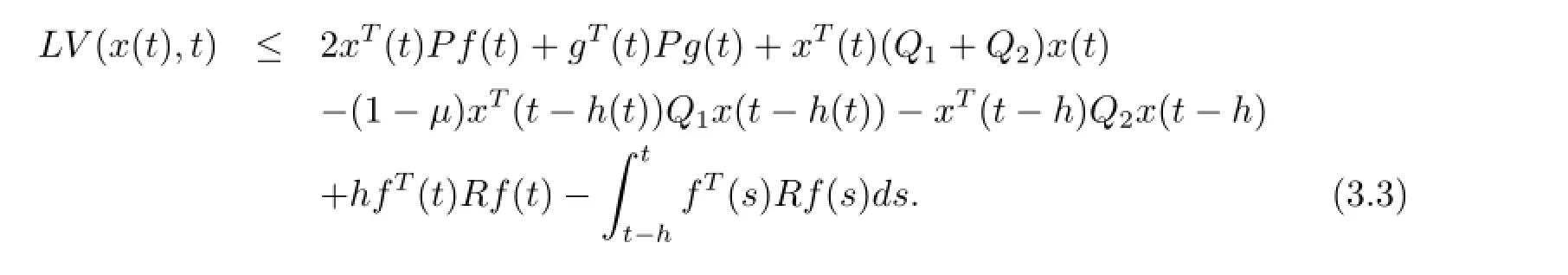
From the Leibniz-Newton formula,the following equations are true for any matrices M and N with appropriate dimensions O
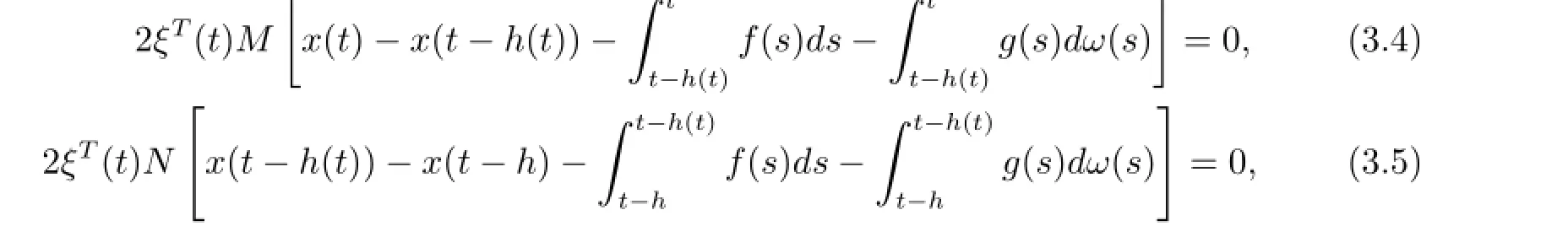
where
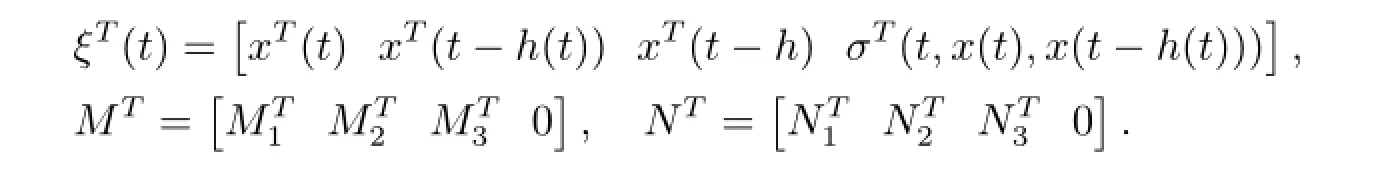
On the other hand, the following equation is also true
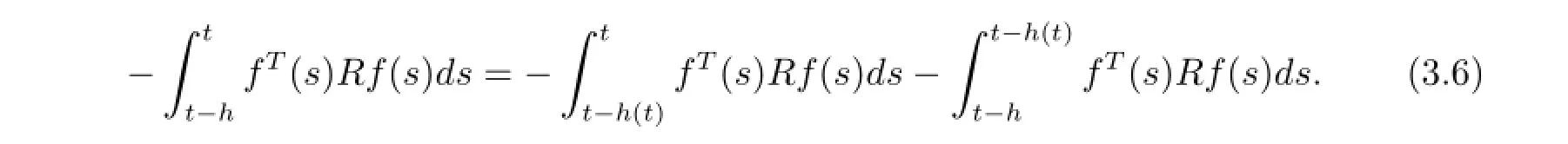
For any positive scalar δ,it follows from(2.4)that
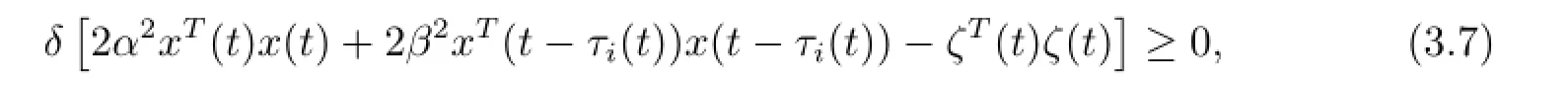
where ζ(t)=σ(t,x(t),x(t-h(t))).
Combining(3.3)-(3.7),we can obtain the following inequality
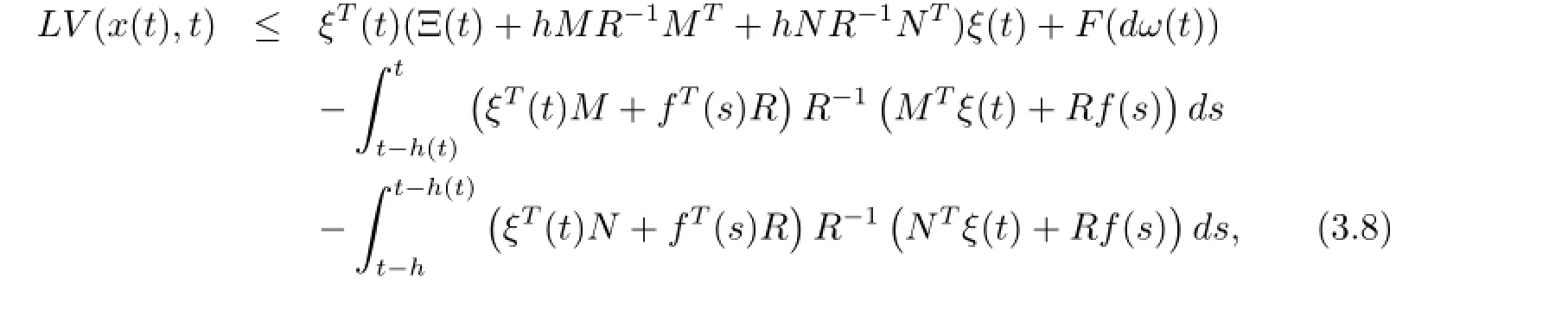
where
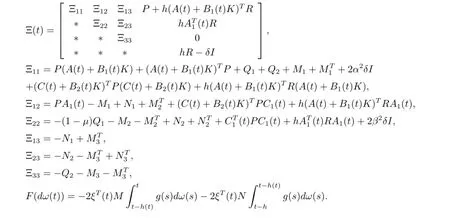
Since R>0,then the last two parts in inequality(3.8)are all less than 0.So,taking the mathematical expectation on both sides of equation(3.2)and using inequality(3.8),since E{F(dω(t))}=0,we can obtain that
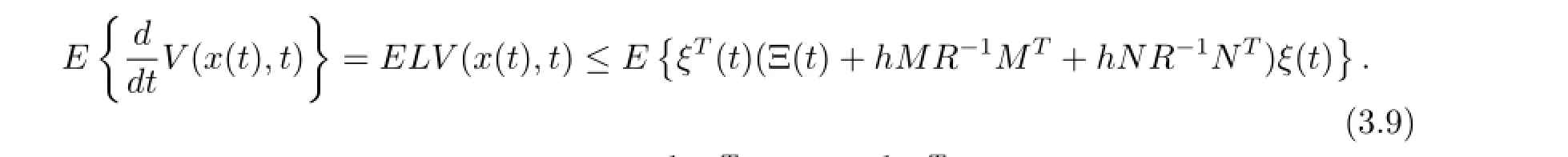
It remains to show that Ξ(t)+hMR-1MT+hNR-1NT<0.Using Schur complement formula,we see that Ξ(t)+hMR-1MT+hNR-1NT<0 if and only if the following matrix inequality holds
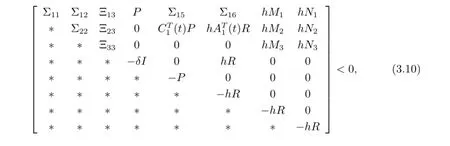
where
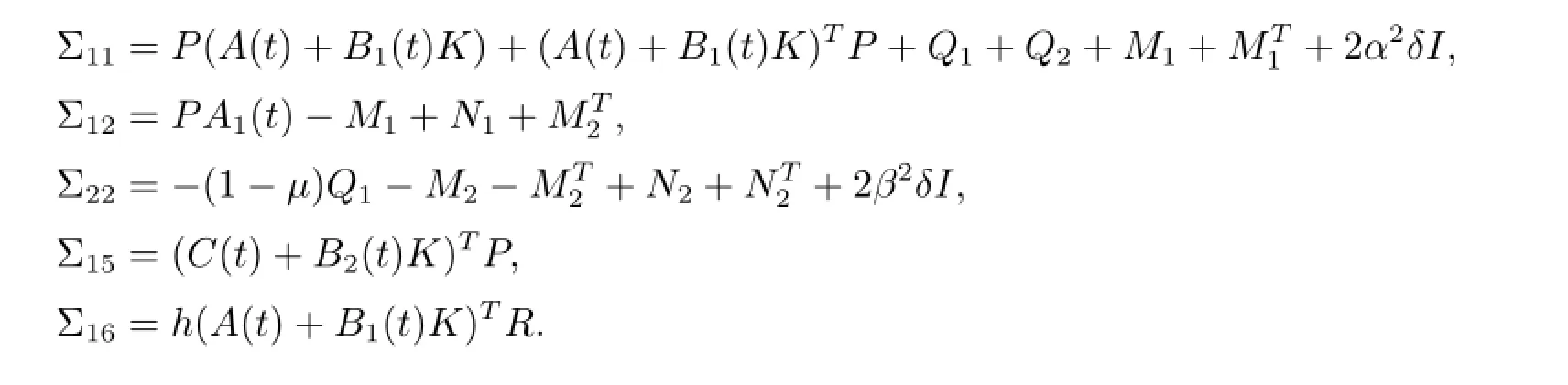
Then premultiplying and postmultiplying inequality(3.10)by
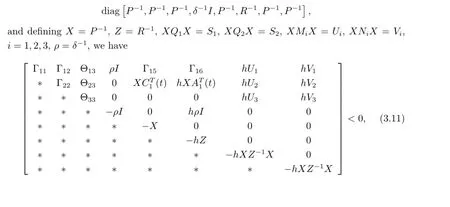
where
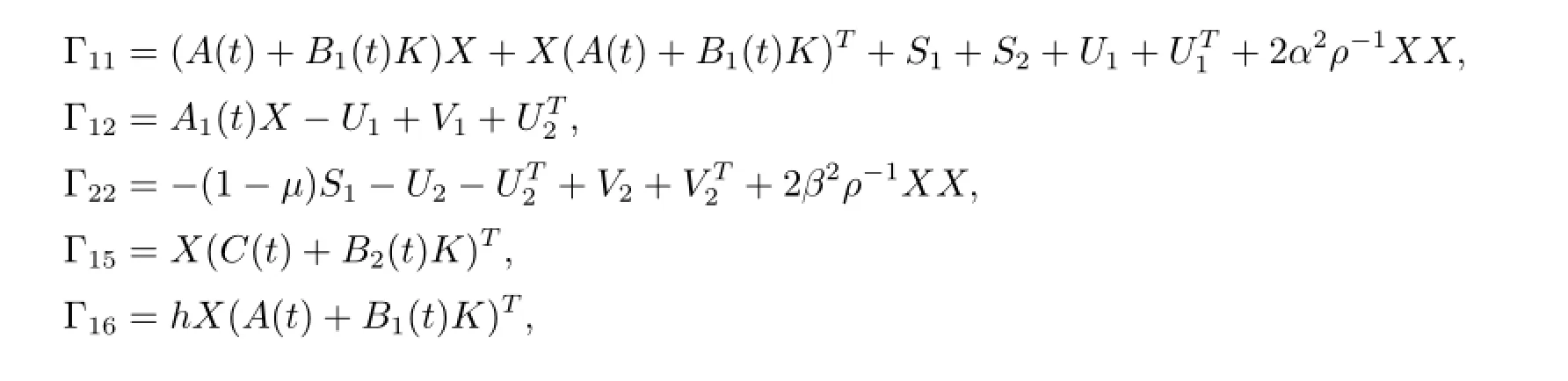
and Θ13,Θ23and Θ33are defined in inequality(3.1).
Noting equation(2.2),and let Y=KX,inequality(3.11)can be written as
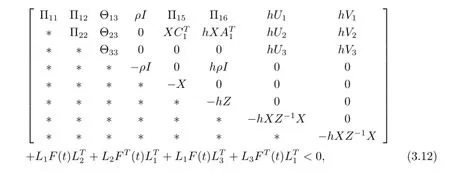
where
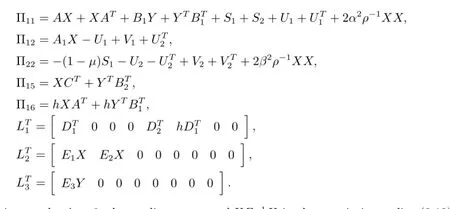
For given scalar λ>0,the nonlinear term-hXZ-1X in the matrix inequality(3.12)can be rewritten as-h(λX)(λ2Z)-1(λX).Therefore,by Lemma 1,we have the inequality -hXZ-1X≤hλ2Z-2hλX.Applying Lemma 2 and Schur complement to inequality (3.12),we can obtain the LMI(3.1)stated in Theorem 1,which means that system(2.1)under control law u(t)=Y X-1x(t)is robust stabilization.This completes the proof.
Remark 1When the differential of h(t)is unknown,and the delay h(t)satisfies 0≤h(t)≤h,by setting S1=0,a delay-dependent and rate-independent criterion for robust stabilization of systems(2.1)from Theorem 1 can be obtained.
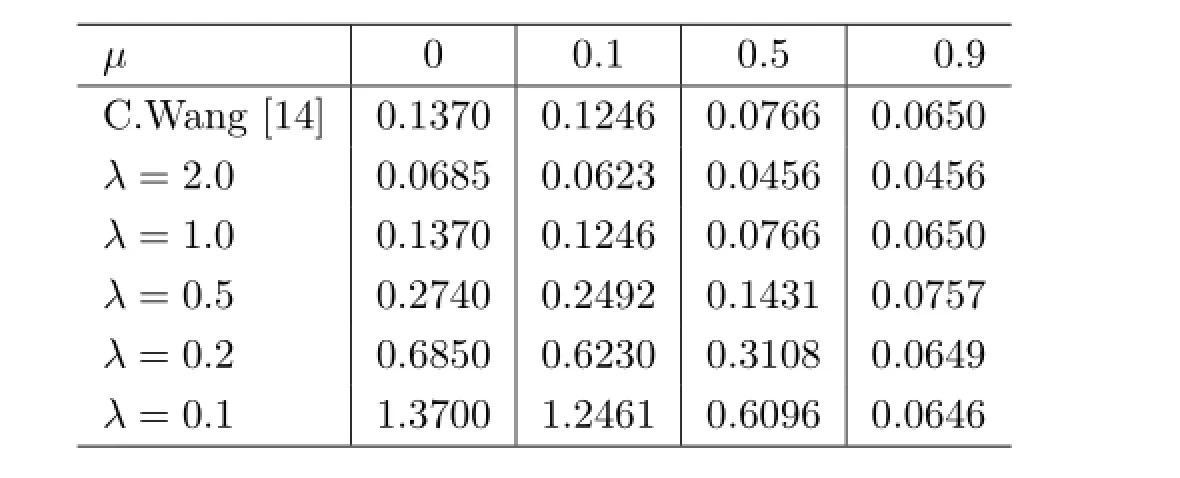
Table 1:(MAUB)h of the time-varying delay h(t)for differentµ.
Remark 2When α=0,β=0,a uncertain linear stochastic differential delay system criterion without nonlinear perturbation for robust stabilization of systems(2.1)from Theorem 1 can be obtained.
4 Numerical Example
In this section,in order to demonstrate the effectiveness of the proposed method,we provide the following numerical example.
Example 1 Consider the uncertain nonlinear single time-delay system(2.1)with the following parameters
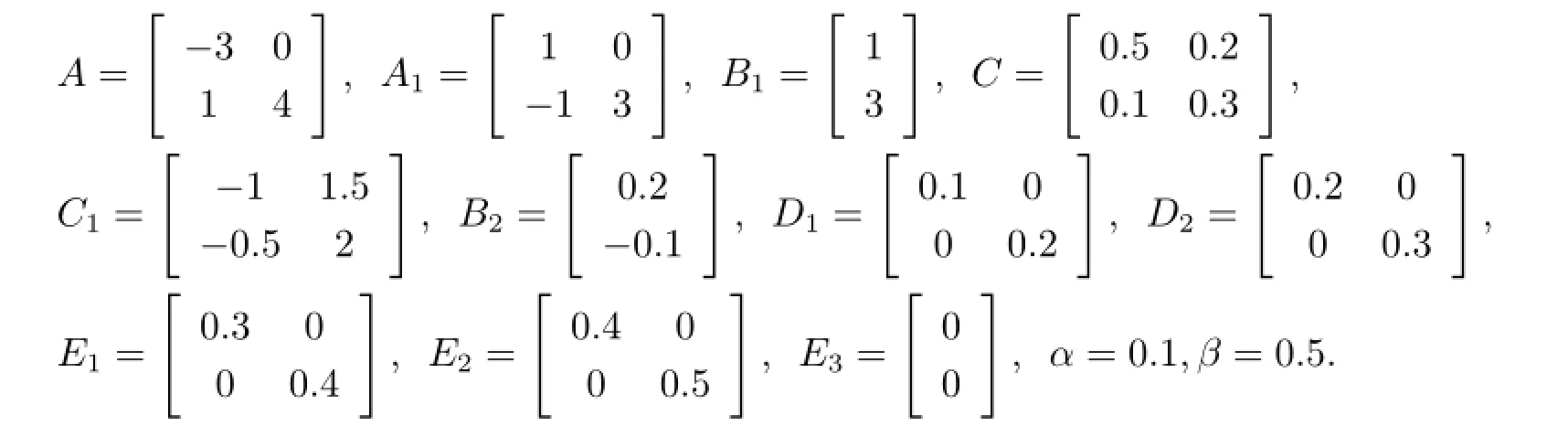
By using matlab solver feasp,for givenµ=0.5,λ=0.2,the feasibility upper bound of h(t)is 0.3108.Choosing h=0.3,according to Theorem 1,solve LMI in inequality(3.1),and get a set of solutions as follows
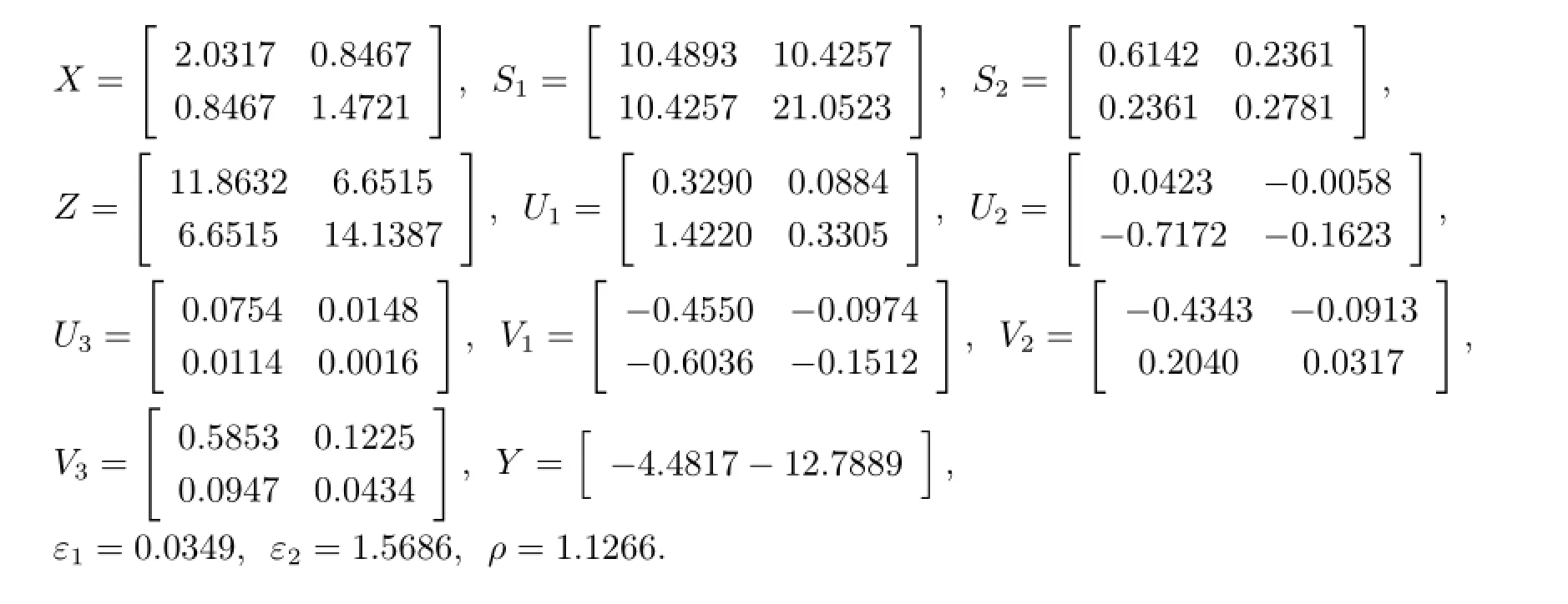
Therefore the robust problem is solvable,and the memoryless feedback gains in control are computed as
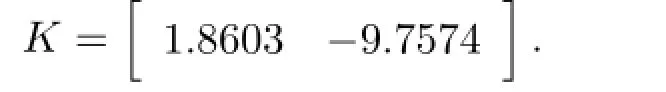
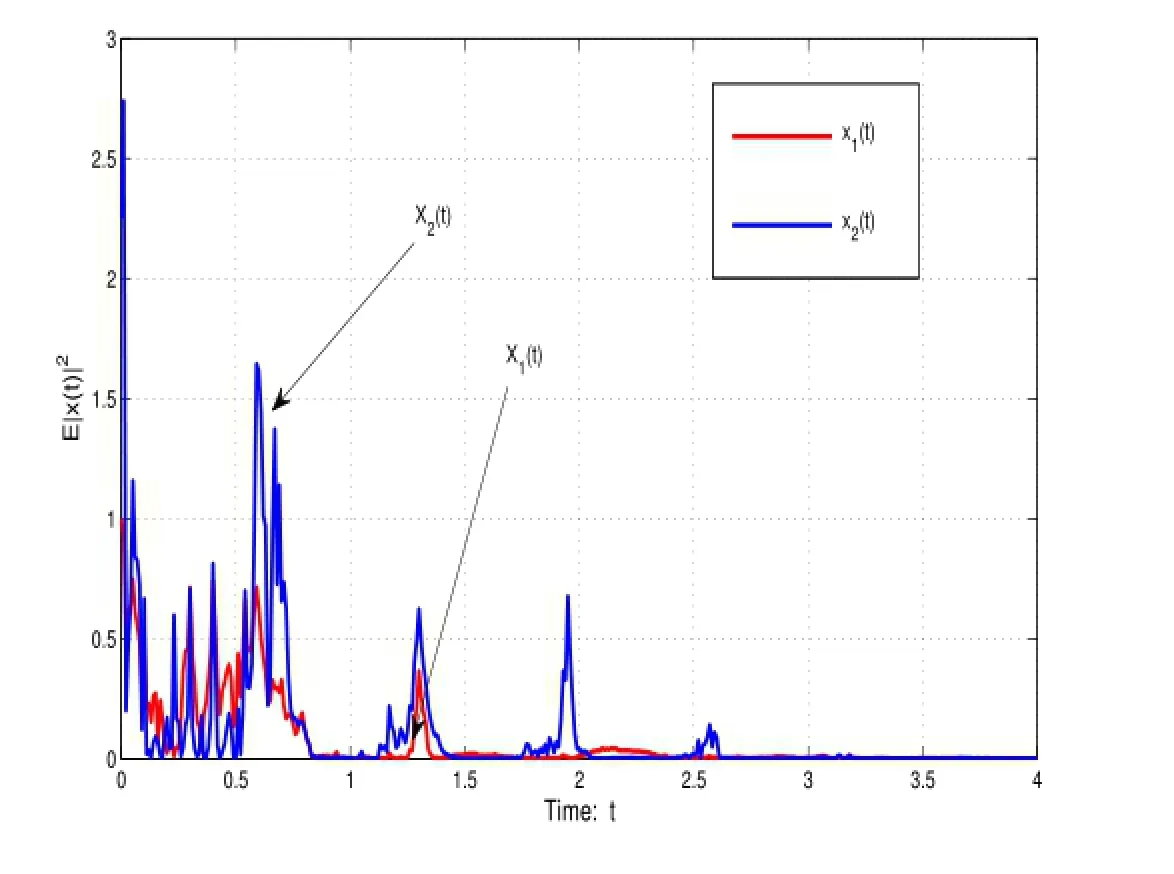
Figure 1:Trajectory of the solution to such system in Example 1
References
[1]Pan Q F,Zhang Z F.Exponential stability of a class of stochastic delay recurrent neural network[J]. J.Math.,2014,34(3):487-496.
[2]Wang Q,Wne J C.Stability of stochastic differential equations with piecewise constant arguments of retarded type[J].J.Math.,2015,35(2):307-317.
[3]Yue D,Han Q L.Delay-dependent exponential stability of stochastic systems with time-varying delay[J].IEEE Trans.Autom.Contr.,2005,50(2):217-222.
[4]Basin M,Rodkina A.On delay-dependent stability for a class of nonlinear stochastic systems with multiple state delays[J].Nonl.Anal.The.Meth.Appl.,2008,68(8):2147-2157.
[5]Li H,Chen B,Zhou Q,Lin C.Delay-dependent robust stability for stochastic time-delay systems with polytopic uncertainties[J].Int.J.Rob.Nonl.Contr.,2008,18(15):1482-1492.
[6]Chen J D.Delay-dependent robust H∞control of uncertain neutral systems with state and input delays:LMI optimization approach[J].Chaos,Soli.Fractals,2007,33(2):595-606.
[7]Xu S,Lam J,Zou Y.Delay-dependent guaranteed cost control of uncertain system with state and input delays[J].IEE Proc.Contr.The.Appl.,2006,153(6):307-313.
[8]Chen W,Guan Z,Lu X.Delay-dependent robust stabilization and H∞control of uncertain stochastic systems with time-varying delay[J].IMA J.Math.Contr.Inf.,2004,21(3):345-358.
[9]Wu M,He Y,She J H,Liu G P.Delay-dependent criteria for robust stability of time-varying delay systems[J].Auto.,2004,40(8):1435-1439.
[10]He Y,Wang Q G,Xie L H,Lin C.Further improvement of free-weighting matrices technique for systems with time-varying delay[J].IEEE Trans.Autom.Contr.,2007,52(2):293-299.
[11]Tian X,Xie L,Chen Y W.Robust non-fragile H∞control for uncertain time delayed stochastic systems with sector constraints[C].Proceedings of IEEE International Confer.Contr.Auto.,2007:1852-1856.
[12]Xu S,Lam J,Yang G,Wang J.Stabilization and H∞control for uncertain stochastic time-delay systems via non-fragile controllers[J].Asian J.Contr.,2006,8(2):197-200.
[13]Zhang J H,Shi P,Yang H J.Non-fragile robust stabilization and H∞control for uncertain stochastic nonlinear time-delay systems[J].Chaos Soli.Fract.,2009,42(5):3187-3196.
[14]Wang C,Shen Y.Delay-dependent non-fragile robust stabilization and H∞control of uncertain stochastic systems with time-varying delay and nonlinearity[J].J.Franklin Insti.,2011,348:2174-2190.
[15]Liu L,Xie X J.State feedback stabilization for stochastic feedforward nonlinear systems with timevarying delay[J].Auto.,2013,49:936-942.
[16]Xia J W,Park J H,Lee T H,Zhang B Y.H∞tracking of uncertain stochastic time-delay systems:Memory state-feedback controller design[J].Appl.Math.Comput.,2014,249:356-370.
[17]Yan H C,Zhang Z,Meng M.Delay-range-dependent robust H∞control for uncertain systems with interval time-varying delays[J].Neurocomput.,2010,73:1235-1243.
具有非线性扰动的不确定随机时变时滞系统的鲁棒镇定
李伯忍
(东莞理工学院计算机学院,广东东莞523808)
本文研究了具有非线性扰动的不确定随机时变时滞系统的鲁棒镇定的问题.构造了适当的Lyapunov-Krasovskii泛函并利用自由权矩阵方法,借助于线性矩阵不等式(LMI)技术,设计了一个无记忆状态反馈控制器,并获得了不确定随机时变时滞系统的时滞依赖鲁棒镇定判据.数值例子及其仿真曲线表明所提出的理论结果是有效的.
自由权矩阵;非线性扰动;时变时滞;反馈控制
MR(2010)主题分类号:93C10;93D09O23;O29
date:2014-12-07Accepted date:2015-04-07
Supported by the Guangdong Province Natural Science Foundation Project (2016A030313130)and the National Natural Science Foundation Project of China(11371154).
Biography:Li Boren(1980-),male,born at Yugan,Jiangxi,doctor,major in analysis and synthesis of the time-delay and uncertain system.
- 数学杂志的其它文章
- SOME RESULTS FOR TWO KINDS OF FRACTIONAL EQUATIONS WITH BOUNDARY VALUE PROBLEMS
- EQUIVALENCE BETWEEN TIME AND NORM OPTIMAL CONTROL PROBLEMS OF THE HEAT EQUATION WITH POINTWISE CONTROL CONSTRAINTS
- PERIODIC SOLUTIONS OF DAMPED IMPULSIVE SYSTEMS
- ESSENTIAL NORMS OF THE GENERALIZED VOLTERRA COMPOSITION OPERATORS
- THE MINIMAL SOLUTION OF A SPECIAL ANTICIPATED BACKWARD STOCHASTIC DIFFERENTIAL EQUATION
- THE APPLICATION OF THE BASIN OF ATTRACTION TO THE EXISTENCE AND UNIQUENESS OF SOLUTIONS FOR THE SECOND ORDER PARABOLIC BOUNDARY VALUE PROBLEM

