变精度粗糙集的近似幂集空间
李露,张贤勇,孙小义
变精度粗糙集的近似幂集空间
李露,张贤勇*,孙小义
(四川师范大学数学与软件科学学院,四川成都 610068)
变精度粗糙集是重要的量化模型,但其近似算子不具有保并性与保交性。本文针对变精度粗糙集,挖掘补平边界(算子),修正近似算子的集合运算,建立近似幂集空间。具体地,构建四种补平边界(算子),分析容错特征;建立近似算子的保并等式与保交等式,重新定义近似集的并交补运算;定义近似幂集空间,得到关于经典幂集空间的同态性质。本文从算子论与集合论的双重视角深化了变精度粗糙集,并量化扩张了定性粗糙集相关结果。
变精度粗糙集;近似算子;集合运算;补平边界(算子);近似幂集空间
引言
粗糙集理论是一种基础的不确定性数学理论,具有数据挖掘的广泛应用。其经典的承载模型为定性模型(记为PawlakRS)[1],具有一定局限性,如数据过拟合。对比地,量化粗糙集模型具有适用性,能有效解决实际的数据噪声问题。概率粗糙集提供了基本的量化框架,具有可测性、泛性与弹性等优点[2]。变精度粗糙集Variable precision rough sets(记为VPRS)则是其中的重要代表。VPRS主要引进错误分类率度量与量化阈值进行建模[3]。从而,VPRS具有相关的错误容忍机制,并扩张了PawlakRS。当前,VPRS具有深入研究。例如,文[4]基于容差关系粒度构建VPRS,从概念格角度扩张PawlakRS;文[5,6]研究VPRS属性约简及算法。特别地,文[7]比较研究VPRS与程度粗糙集,并针对粗糙集量化提出基于相对量化与绝对量化的双量化完备刻画。
粗糙集理论具有“算子论”与“集合论”两种解释[8]。“算子论”认为,粗糙集理论是在经典集合算子上添加了上、下近似两个一元算子,是经典集合理论的拓展;而“集合论”认为,粗糙集理论没有引进新的算子,只是改变了集合的运算。在传统的定性模型中,近似算子部分保持集合并交运算。针对剩余的不保持部分,文[9]挖掘补平边界(算子),定义近似的新型并交补运算,确立近似算子保持集合运算的良性,进而构建近似幂集空间。
VPRS近似算子完全不保持集合并交运算。对此,本文主要基于文[9]的研究,拟将良性集合运算从定性近似算子拓展到量化VPRS近似算子,并最终建立基于新型集合运算的VPRS近似幂集空间。具体地,针对VPRS,引入四种边界(算子)进行修正;重新定义近似集的集合运算,得到近似算子对集合运算的保持良性;确立近似幂集空间,并分析对于常规幂集空间的同态特性。相关研究将从“算子论”和“集合论”深化VPRS,并量化扩张已有的PawlakRS定性结果。
1 粗糙集与近似算子性质
本节基于文[1,3,8]回顾PawlakRS与VPRS,并提供相应的定性与定量近似算子的性质。这里,论域与等价关系组建近似空间,对象的等价类表示知识粒,为目标概念,符号表示集合补运算。
定义1 PawlakRS中,上下近似定义如下:
性质1 PawlakRS上下近似算子对于集合并交运算具有性质:
PawlakRS即为经典定性粗糙集,其近似算子具有不完全的保并性与保交性(性质1)。对此,文[9]进行了等式修正,下面提供一种变形刻画。
性质2 PawlakRS中,两种补平边界(算子)能够修正近似算子的并交运算到如下等式:
针对PawlakRS近似算子的非保并性与非保交性(性质1),定义2提出两种补平边界(算子),性质2得到近似算子的并交运算等式。进而,文[9]还提出近似集的新型并交补运算与近似幂集空间,获得运算保持与同态良性。
针对PawlakRS量化缺陷,VPRS引入错误分类率与量化阈值确立模型。粒关于概念的错误分类率为:
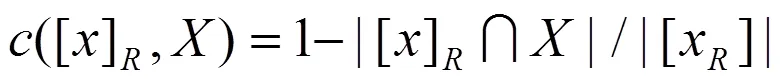
定义3 VPRS中,上下近似定义如下:
性质4 VPRS上下近似算子对于集合并交运算具有如下不等式:
对比性质1与性质4可见,在量化扩张过后,VPRS近似算子完全不保持集合并交运算,相关等式补平成为一个问题。
2 变精度粗糙集的补平边界与补平算子
针对VPRS算子实施集合并交运算的不等性(性质3),本节主要建立四种补平边界与补平算子。
引理1 VPRS近似算子具有如下作差性质:
引理1主要基于性质4实施作差比较,挖掘影响等式的集合因素。其正确性可由VPRS近似算子定义(定义3)保证。引理1揭示了性质4中VPRS近似算子并交不保持的差额部分,进而自然确定四种边界(算子)以实施补平作用。
它们分别称为上内边界、上外边界、下内边界、下外边界,统称为补平边界。其中,
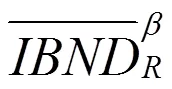
定理1 VPRS中,四种补平边界(算子)修正近似算子的并交运算到如下等式:
定理2 VPRS四种补平边界(算子)量化扩张了PawlakRS补平边界(算子),后者是前者的特殊情况。时的具体退化结果如下:
根据引理1,定义4自然确立四种边界(算子)。在定理1中,补平边界(算子)通过差额修正,自然补平VPRS近似算子对集合的并交运算。因此,定理1改进性质4中的不等式为等式。此外,定理2表明VPRS补平边界(算子)对于PawlakRS补平边界(算子)的量化扩张性,其中有两种VPRS补平边界在时退化为空集。
VPRS补平边界与补平算子具有意义。关于“算子论”,四种边界算子被引入,并能实施VPRS补平功能;关于“集合论”,四种边界集合被引入,并调平VPRS近似算子的集合并交运算。此外,相关结果扩张了PawlakRS的基本结果。
鉴于边界与算子的一致性,下面主要聚焦补平边界作深入分析。首先,依据定义4,可以归纳四种边界的错误分类率特征,如表1。

表1 四种边界的错误分类率特征
基于定义4与表1,可以基本定位四种边界。为此,下面给出相关的图1。其中,集合为一般的相交关系,相关小矩形描述四种边界(或其组成粒)。
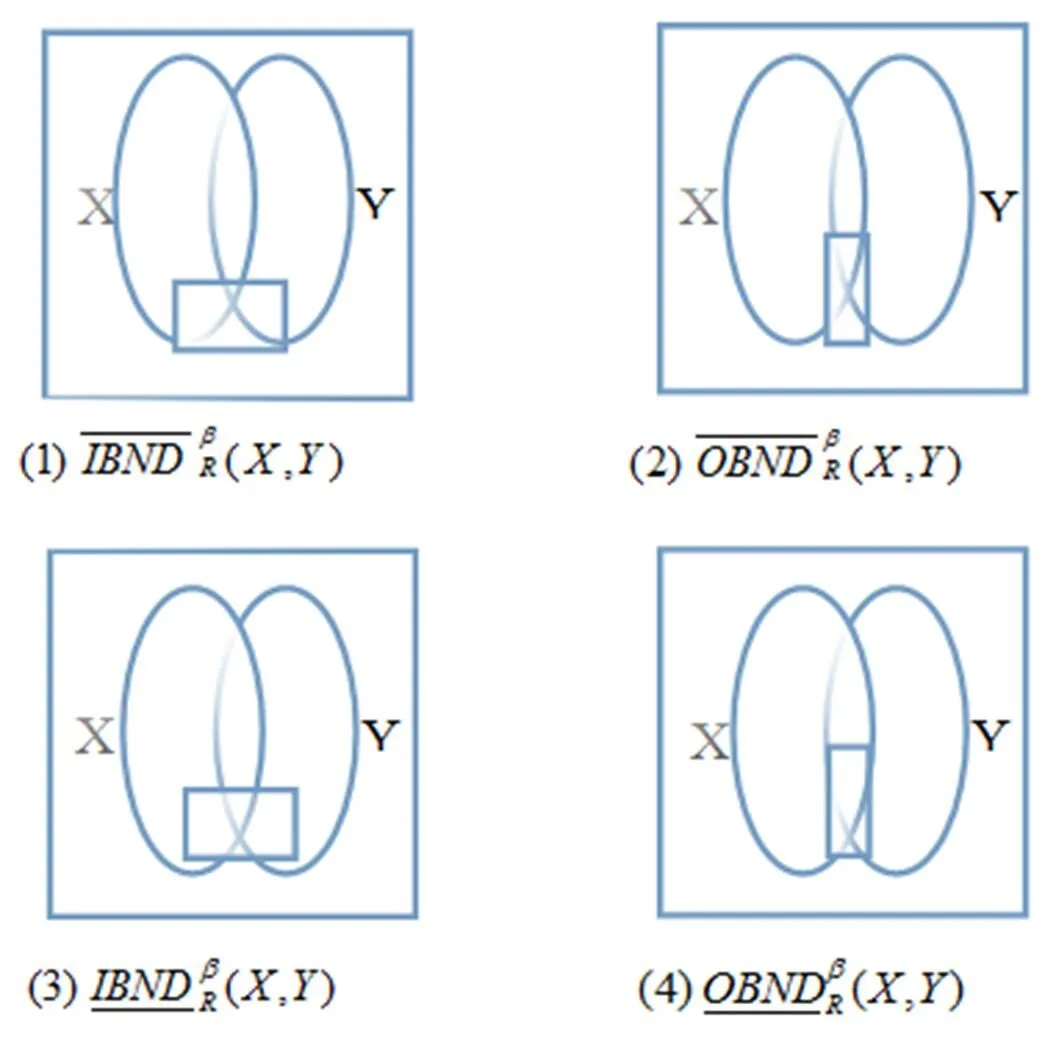
图1 VPRS的四个补平边界示意图
3 变精度粗糙集的近似幂集空间
基于上节的VPRS补平边界与补平算子,可以构造VPRS近似的新型并交运算,得到保持并交运算的良性。再加上对补运算的重新定义,本节主要构建VPRS近似幂集空间,并分析相关的同态性质。
根据补平边界(算子)及近似算子的补运算,定义5提出了VPRS近似的一种新型并交补运算。适用于VPRS近似但依赖于基础概念,与经典的不同,具有相关的修正。可视为的推广,因为细化为单点粒结构时前者退化为后者,且概念精确可定义时两者变得一致。两者可以根据应用环境进行区别确认。
证明 前四条由引理1、定理1与定义5可得。基于定义5与VPRS性质,
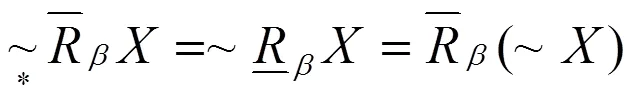
即(5)得证,同理可证(6)。□
定理3表明,VPRS上下近似算子能够保持集合并交补运算。因此,新增加的具有意义,特别是从“集合论”角度。对VPRS近似运算具有封闭性,因此能够组建相关的代数空间。下面定义VPRS近似幂集空间,并分析同态性质。
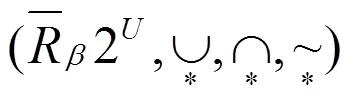
VPRS近似幂集空间的对象是确定的,但其依赖于幂集空间,因为近似集的运算具有对基础概念的依赖性。
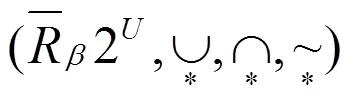
的同态满射。
4 结论
PawlakRS具有定性绝对性,文[9]针对PawlakRS近似算子性质,提出两种补平边界与补平算子,获取近似算子对集合运算的相等式与保持性,并最终建立近似幂集空间。本文主要在文[9]的基础上,将相关工作向量化VPRS进行了扩张推广。针对VPRS,构造了四种补平边界与补平算子,构建了新型的并交补运算(即),让近似算子具有保持集合运算的良性,进而构建的近似幂集空间具有对于经典幂集空间的同态特性。此外,所得VPRS结果具有对于PawlakRS相关结果的量化扩张性。
本文研究深化了VPRS。从“算子论”的角度,添加四个二元算子,把现有的VPRS系统
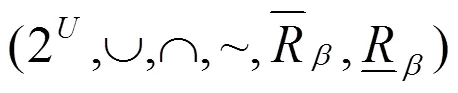
推进到
[1] PAWLAK Z. Rough sets [J]. International Journal of Computer and Information Sciences, 1982, 11(5): 341-356.
[2] Yao Y. The superiority of three-way decisions in probabilistic rough set models [J]. Information Sciences, 2011, 181(6): 1080-1096.
[3] WOJCIECH Z. Variable precision rough sets model [J]. Journal of Computer and System Sciences, 1993, 46: 39-59.
[4] KANG X P, MIAO D Q. A variable precision rough set model based on the granularity of tolerance relation [J]. Knowledge-Based Systems, 2016, 102: 103-115.
[5] CHEN D G, YANG Y Y, DONG Z. An incremental algorithm for attribute reduction with variable precision rough sets [J]. Applied Soft Computing, 2016, 45: 129-149.
[6] Mi J S, Wu W Z, Zhang W X. Approaches to knowledge reduction based on variable precision rough set model [J]. Information sciences, 2004, 159(3-4): 255-272.
[7] ZHANG X Y, MO Z W, XIONG F, et al. Comparative study of variable precision rough set model and graded rough set model [J]. International Journal of Approximate Reasoning, 2012, 53(1): 104-116.
[8] Yao Y Y. Two views of the theory of rough sets in finite universes [J]. International of Approximate Reasoning, 1996, 15: 291-317.
[9] Zhang X Y, Mo Z W, Shu L. Operators of approximation and approximate power sets space [J]. Journal of Electronic Science and Technology of China, 2004, 2(2): 91-96.
[10] XU W H, GUO Y T. Generalized multigranulation double-quantitative decision-theoretic rough set [J]. Knowledge-Based Systems, 2016, 105: 190-205.
Approximate Power Set Space of Variable Precision Rough Sets
LI Lu, ZHANG Xianyong*, SUN Xiaoyi
(College of Mathematics and Software Science, Sichuan Normal University, Chengdu 610068, China)
Variable precision rough sets (VPRS) act as a fundamental quantitative model, but their approximation operators can not maintain intersection and union operations. Aiming at VPRS, this paper mines supplement boundaries (operators), amends set operations of approximation operators, and constructs approximate power set space. Concretely, four types of supplement boundaries (operators) are proposed, and their fault-tolerance features are analyzed; intersection and union preservation equations of approximation operators are gained, so union, intersection, and complement operators of approximations are redefined; approximate power set space is determined, and its homomorphism feature regarding the classical power set space is achieved. This study adopts double views of operators and sets to enrich VPRS, and quantitatively expands relevant results of qualitative rough sets.
variable precision rough set; approximation operator; set operation; supplement boundary (operator); approximate power set space
1672-9129(2016)01-0006-05
TP18
A
2016-06-17;
2016-06-27。
国家自然科学基金项目61203285;四川省教育厅科研项目15ZB0028。
李露(1993-),女,重庆云阳人,硕士研究生,主要研究方向:粗糙集、数据挖掘;张贤勇(*通信作者、第一作者)(1978-),男,四川成都人,副教授,博士后,硕导,主要研究方向:粗糙集、粒计算、数据挖掘;孙小义(1992-),女,四川达州人,硕士研究生,主要研究方向:粗糙集、数据挖掘。
(*通信作者电子邮箱:xianyongzh@sina.com)

