Characterizations of Null Holomorphic Sectional Curvature of GCR-Lightlike Submanifolds of Indefinite Nearly K¨ahler Manifolds
RachnaRani,SangeetKumar,RakeshKumarandR.K.Nagaich
1Department of Mathematics,University College,Moonak 148033,Punjab,India
2Department of Mathematics,Sri Guru Teg Bahadur Khalsa College,Sri Anandpur Sahib 140118,Punjab,India
3Department of Basic and Applied Sciences,Punjabi University,Patiala 147002,Punjab,India
4Department of Mathematics,Punjabi University,Patiala 147002,Punjab,India
Characterizations of Null Holomorphic Sectional Curvature of GCR-Lightlike Submanifolds of Indefinite Nearly K¨ahler Manifolds
RachnaRani1,SangeetKumar2,RakeshKumar3,∗andR.K.Nagaich4
1Department of Mathematics,University College,Moonak 148033,Punjab,India
2Department of Mathematics,Sri Guru Teg Bahadur Khalsa College,Sri Anandpur Sahib 140118,Punjab,India
3Department of Basic and Applied Sciences,Punjabi University,Patiala 147002,Punjab,India
4Department of Mathematics,Punjabi University,Patiala 147002,Punjab,India
.We obtain the expressions for sectional curvature,holomorphic sectional curvature and holomorphic bisectional curvature of a GCR-lightlike submanifold of an indefinite nearly K¨ahler manifold and obtain characterization theorems for holomorphic sectional and holomorphic bisectional curvature.We also establish a condition for a GCR-lightlike submanifold of an indefinite complex space form to be a null holomorphically flat.
Indefinite nearly K¨ahler manifold,GCR-lightlike submanifold,holomorphic sectional curvature,holomorphic bisectional curvature.
AMS Subject Classifications:53C15,53C40,53C50
1 Introduction
Due to the growing importance of lightlike submanifolds in mathematical physics and relativity[5]and the significant applications of CR structures in relativity[3,4],Duggal and Bejancu[5]introduced the notion of CR-lightlike submanifolds of indefinite K¨ahler manifolds.Contrary to the classical theory of CR-submanifolds,CR-lightlike submanifolds do not include complex and totally real lightlike submanifolds as subcases.Therefore Duggal and Sahin[7]introduced SCR-lightlike submanifolds of indefinite K¨ahler manifold which contain complex and totally real subcases but do not include CR andSCR cases.Therefore Duggal and Sahin[8]introduced GCR-lightlike submanifolds of indefinite K¨ahler manifolds,which behaves as an umbrella of complex,totally real,screen real and CR-lightlike submanifolds and further studied by[11-13].Husain and Deshmukh[10]studied CR submanifolds of nearly K¨ahler manifolds.Recently,Sangeet et al.[14]introduced GCR-lightlike submanifolds of indefinite nearly K¨ahler manifolds and obtained their existence in indefinite nearly K¨ahler manifolds of constant holomorphic sectional curvature c and of constant type α.In present paper,we obtain the expressions for sectional curvature,holomorphic sectional curvature and holomorphic bisectional curvature of a GCR-lightlike submanifold of an indefinite nearly K¨ahler manifold and obtain characterization theorems for holomorphic sectional and holomorphic bisectional curvature.
2 Lightlike submanifolds
Let(¯M,¯g)be a real(m+n)-dimensional semi-Riemannian manifold of constant index q such that m,n≥1,1≤q≤m+n-1 and(M,g)be an m-dimensional submanifold of¯M and g be the induced metric of¯g on M.If¯g is degenerate on the tangent bundle TM of M then M is called a lightlike submanifold of¯M,for detail see[5].For a degenerate metric g on M,TM⊥is a degenerate n-dimensional subspace of Tx¯M.Thus both TxM and TxM⊥are degenerate orthogonal subspaces but no longer complementary.In this case,there exists a subspace RadTxM=TxM∩TxM⊥which is known as radical(null)subspace.If the mapping RadTM:x∈M-→RadTxM,defines a smooth distribution on M of rank r>0 then the submanifold M of¯M is called an r-lightlike submanifold and RadTM is called the radical distribution on M.Screen distribution S(TM)is a semi-Riemannian complementary distribution of Rad(TM)in TM therefore

and S(TM⊥)is a complementary vector subbundle to RadTM in TM⊥.Let tr(TM)and ltr(TM)be complementary(but not orthogonal)vector bundles to TM in T¯M|Mand to RadTM in S(TM⊥)⊥respectively.Then we have

Let u be a local coordinate neighborhood of M and consider the local quasi-orthonormal fields of frames of¯M along M,on u as{ξ1,···,ξr,Wr+1,···,Wn,N1,···,Nr,Xr+1,···,Xm},where{ξ1,···,ξr},{N1,···,Nr}are local lightlike bases of Γ(RadTM|u),Γ(ltr(TM)|u)and{Wr+1,···,Wn},{Xr+1,···,Xm}are local orthonormal bases of Γ(S(TM⊥)|u)and Γ(S(TM)|u)respectively.For these quasi-orthonormal fields of frames,we have
Theorem 2.1(see[5]).Let(M,g)be an r-lightlike submanifold of a semi-Riemannian manifold(¯M,¯g).Then there exists a complementary vector bundle ltr(TM)of RadTM in S(TM⊥)⊥anda basis of ltr(TM)|uconsisting of smooth section{Ni}of S(TM⊥)⊥|u,where u is a coordinate neighborhood of M such that

Let¯∇be the Levi-Civita connection on¯M then according to the decomposition(2.2b),the Gauss and Weingarten formulas are given by
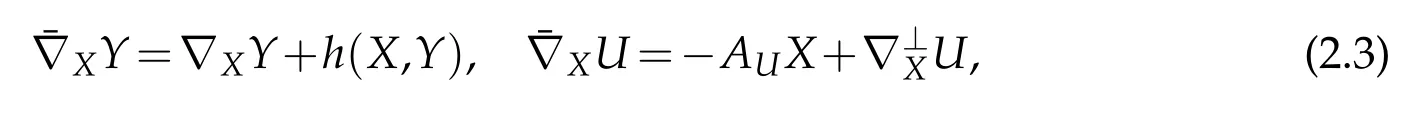
forany X,Y∈Γ(TM)and U∈Γ(tr(TM)),where{∇XY,AUX}and{h(X,Y),∇⊥XU}belong to Γ(TM)and Γ(tr(TM)),respectively.Here∇is a torsion-free linear connection on M,h is a symmetric bilinear form on Γ(TM)which is called second fundamental form,AUis a linear a operator on M and known as shape operator.
According to(2.2a)considering the projection morphisms L and S of tr(TM)on ltr(TM)and S(TM⊥)respectively,then(2.3)become

As hland hsare Γ(ltr(TM))-valued and Γ(S(TM⊥))-valued respectively,therefore theyare called thelightlike secondfundamental formand thescreensecondfundamental form on M.In particular

where X∈Γ(TM),N∈Γ(ltr(TM))and W∈Γ(S(TM⊥)).Using(2.4)and(2.5)we obtain

for any W∈Γ(S(TM⊥)).Let P be the projection morphism of TM on S(TM)then using(2.1),we can induce some new geometric objects on the screen distribution S(TM)on M as
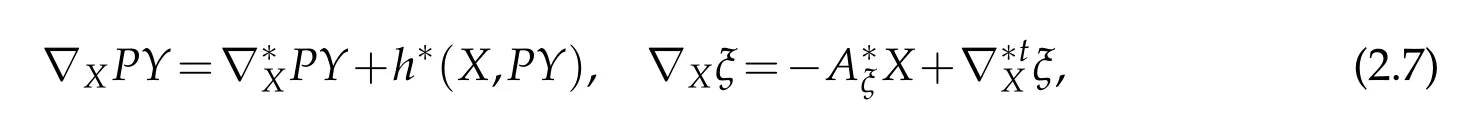
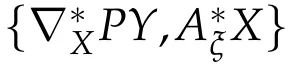
Using(2.4)and(2.7),we obtainfor any X,Y∈Γ(TM),ξ∈Γ(Rad(TM))and N∈Γ(ltr(TM)).

In general,the induced connection∇on M is not a metric connection.Since¯∇is a metric connection,by using(2.4),we get

However,it is important to note that∇∗is a metric connection on S(TM).
Denote by¯R and R the curvature tensors of¯∇and∇respectively then by straightforward calculations(see[5]),we have

where
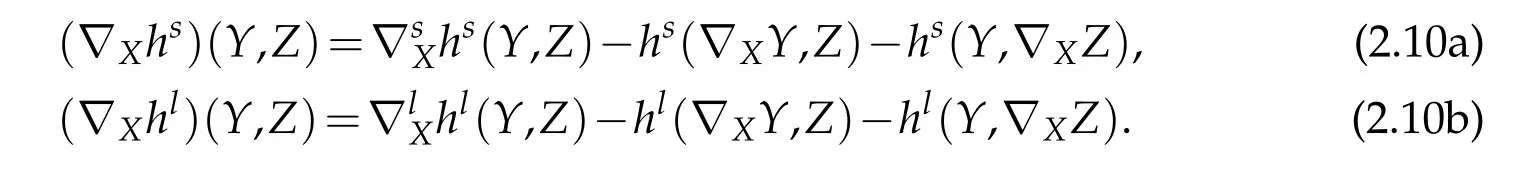
Then Codazzi equation is given respectively by

Gray[9],defined nearly K¨ahler manifolds as
Definition 2.1.Let(¯M,¯J,¯g)be an indefinite almost Hermitian manifold and¯∇be the Levi-Civita connection on¯M with respect to¯g.Then¯M is called an indefinite nearly K¨ahler manifold if

or equivalently
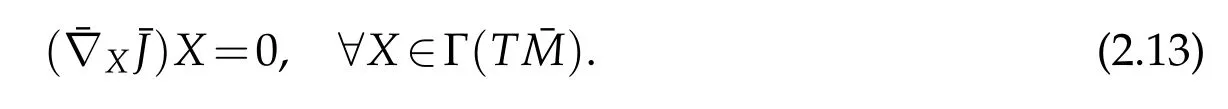
It is well known that every K¨ahler manifold is a nearly K¨ahler manifold but converse is not true.S6with its canonical almost complex structure is a nearly K¨ahler manifold but not a K¨ahler manifold.Due to rich geometric and topological properties,the study of nearly K¨ahler manifolds is as important as that of K¨ahler manifolds.Therefore we studied the geometryof CR,SCR and GCR-lightlike submanifolds of an indefinite nearly K¨ahler manifolds in[14].
Nearly K¨ahler manifold of constant holomorphic curvature c is denoted by¯M(c)and its curvature tensor field¯R is given by,[15]

and the sectional curvature is given by
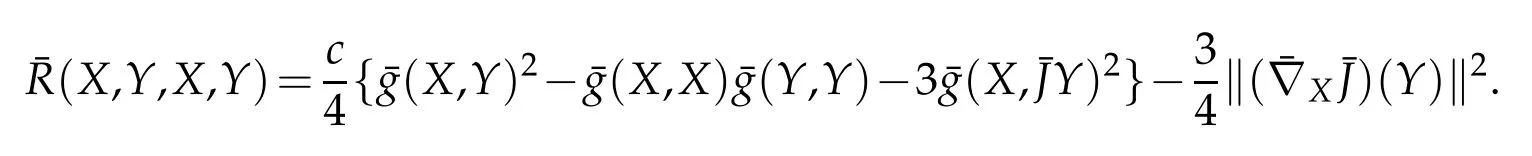
A nearly K¨ahler manifold is said to be of constant type α[9],if there exists a real valued C∞function α on¯M such that

3 Generalized Cauchy-Riemann lightlike submanifolds
In this section,we briefly recall generalized Cauchy-Riemann(GCR)-lightlike submanifold of an indefinite nearly K¨ahler manifold(¯M,¯g,¯J),for detail see[14].
Definition3.1(see[14]).Let(M,g,S(TM))be a real lightlike submanifold ofan indefinite nearly K¨ahler manifold(¯M,¯g,¯J)then M is called a generalized Cauchy-Riemann(GCR)-lightlike submanifold if the following conditions are satisfied
(A)There exist two subbundles D1and D2of Rad(TM)such that
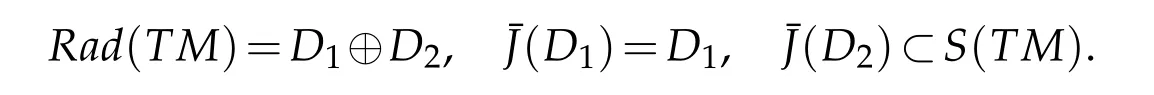
(B)There exist two subbundles D0and D′of S(TM)such that
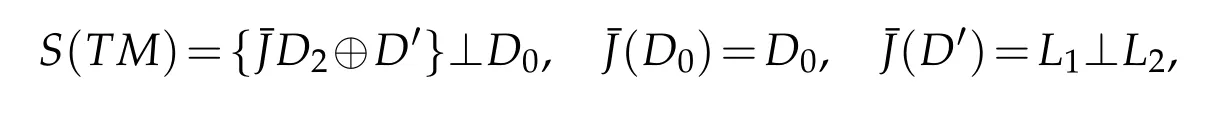
where D0is a non degenerate distribution on M,L1and L2are vector subbundles of ltr(TM)and S(TM)⊥respectively.
Then the tangent bundle TM of M is decomposed as
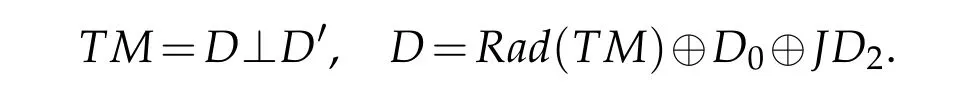
M is called a proper GCR-lightlike submanifold if D1/={0},D2/={0},D0/={0}and L2/={0}.
Let Q,P1and P2be the projections on D,¯J(L1)=M1and¯J(L2)=M2,respectively. Then for any X∈Γ(TM),we have X=QX+P1X+P2X,applying¯J both sides,we obtain

and we can write the Eq.(3.1)as

where TX and wX are the tangential and transversal components of¯JX,respectively. Similarly

for any V∈Γ(tr(TM)),where BV and CV are the sections of TM and tr(TM)respectively.Applying¯J to(3.2)and(3.3),we get T2=-I-Bω,and C2=-I-ωB.Using nearly K¨ahlerian property of¯∇with(2.5),we have the following lemma.
Lemma 3.1(see[14]).Let M be a GCR-lightlike submanifold of an indefinite nearly K¨ahler manifold¯M.Then we have

and
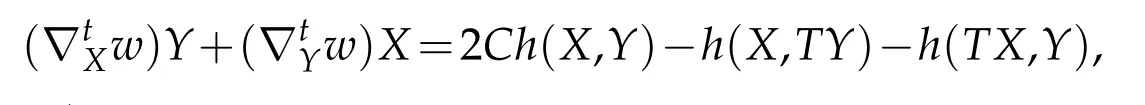
for any X,Y∈Γ(TM),where

4 Holomorphic sectional curvature of a GCR-lightlike submanifold
Let¯M be an indefinite nearly K¨ahler manifold of constant holomorphic curvature c the using(2.9)and(2.14)for any X,Y,Z,W vector fields on TM,we obtain

Using(2.6)in(4.1),we obtain

Thenthe sectional curvature KM(X,Y)=g(R(X,Y)Y,X)of M determinedby orthonormal vectors X and Y of Γ(D0⊕M2)and given by
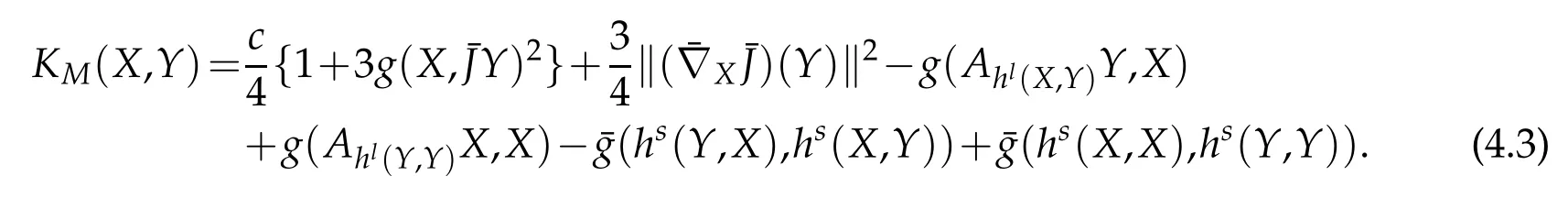
Corollary 4.1.Let M be a GCR-lightlike submanifold of an indefinite nearly K¨ahler manifold of constant holomorphic sectional curvature c.Then sectional curvature of M is given by
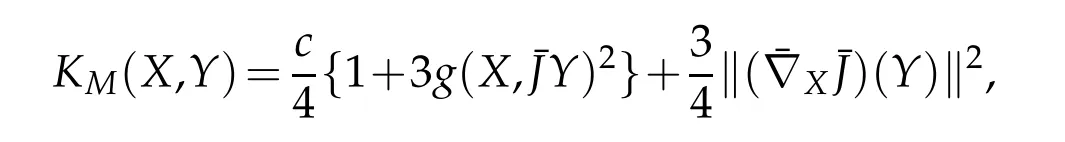
if
(i)M2defines a totally geodesic foliation in¯M.
从图6中不难发现,当单片机DAC接口PA4为低电平时,MOS管2N7002截止,白炽灯光源熄灭,而当单片机DAC接口PA4为高电平时,MOS管2N7002导通,白炽灯光源处于工作状态。该电路能够实时调制红外光信号,降低外界环境光照的影响,并达到延长红外光源使用寿命的目的。
(ii)D0defines a totally geodesic foliation in¯M.
(iii)M is totally geodesic in¯M.
Definition 4.1.The holomorphic sectional curvature H(X)=g(R(X,¯JX)¯JX,X)of M determined by a unit vector X∈Γ(D0)is the sectional curvature of a plane section{X,¯JX}.
Then using(2.8)and(4.3),for a unit vector field X∈Γ(D0),we get


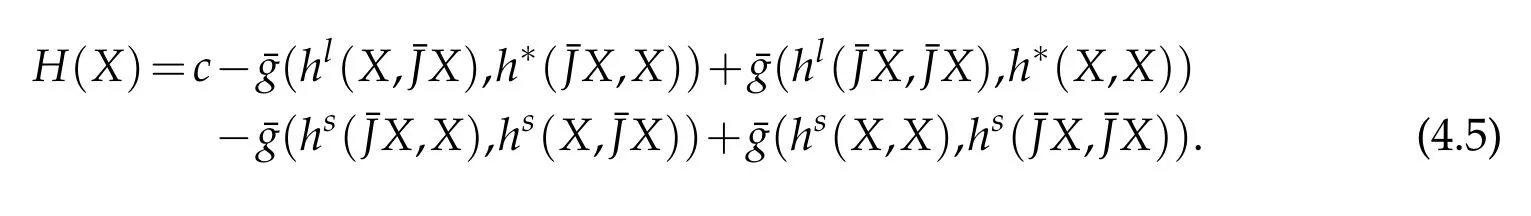
Theorem 4.1(see[14]).Let M be a GCR-lightlike submanifold of an indefinite nearly K¨ahler manifold¯M then the distribution D is integrable if and only if h(X,¯JY)=h(Y,¯JX),for any X,Y∈Γ(D).
Theorem 4.2.Let M be a GCR-lightlike submanifold of an indefinite nearly K¨ahler manifold ¯M(c)with constant holomorphic sectional curvature c and the distribution D0is integrable then H(X)≤c for any unit vector field X∈Γ(D0).
Proof.Since D0is integrable therefore using the Theorem 4.1,we have h(¯JX,¯JX)= -h(X,X),for any unit vector field X∈Γ(D0).Therefore from(4.5),we obtain
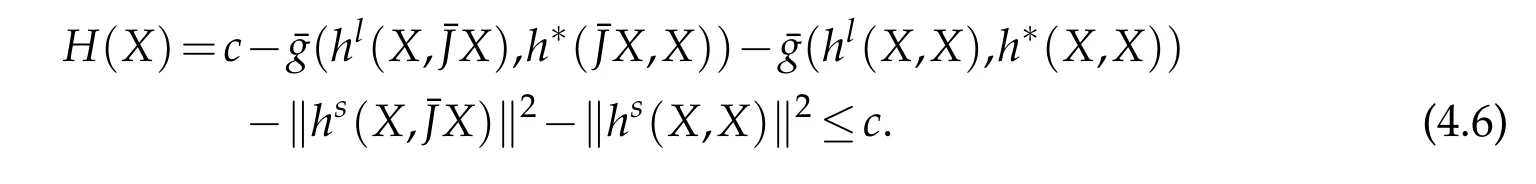
Definition 4.2.A GCR-lightlike submanifold M of an indefinite nearly K¨ahler manifold ¯M is said to be D-totally geodesic(resp.D′-totally geodesic)if and only if h(X,Y)=0 for any X,Y∈Γ(D0)(resp.X,Y∈Γ(D′)).
Lemma 4.1.Let M be a GCR-lightlike submanifold of an indefinite nearly K¨ahler manifold¯M. If the distribution D0defines a totally geodesic foliation in¯M then M is D0-geodesic.
Proof.To show M is D0-geodesic we have to prove

for any X,Y∈Γ(D0),ξ∈Γ(Rad(TM))and W∈Γ(S(TM⊥)).Since D0defines totally geodesic foliation in¯M therefore we obtain

and

Hence the assertion follows.
Theorem 4.3.Let M be a GCR-lightlike submanifold of an indefinite nearly K¨ahler manifold¯M with constant holomorphic sectional curvature c.If D0defines a totally geodesic foliation in¯M then H(X)=c,for any unit vector field X∈Γ(D0).
Proof.The assertion follows directly using the Lemma 4.1 in(4.5).
Theorem 4.4.Let M be a GCR-lightlike submanifold of an indefinite nearly K¨ahler manifold¯M of constant type α and of constant holomorphic sectional curvature c.If M is M2-totally geodesic then

where KM(X,Y)is the sectional curvature of the plane section X∧Y in M2⊂D′.
Proof.Let plane section X∧Y is spanned by the orthonormal unit vectors X,Y∈Γ(M2)⊂Γ(D′),then using(2.8)in(4.3),we get
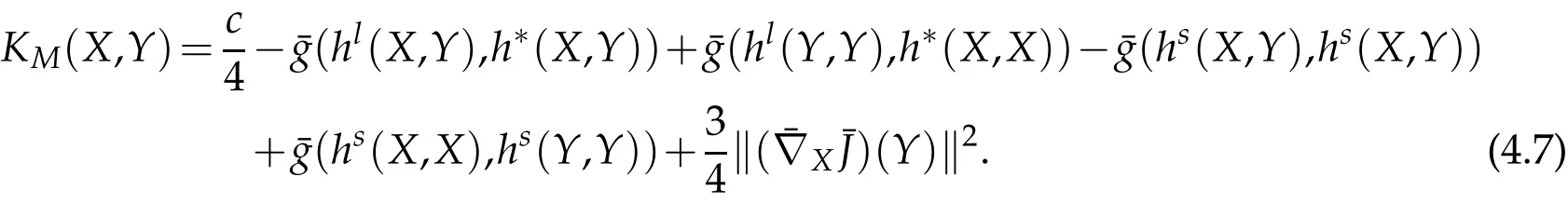
Since¯M is of constant type α,using(2.15)we obtain

Using the hypothesis that M is M2-totally geodesic in(4.8),the assertion follows.
Definition 4.3.The holomorphic bisectional curvature for the pair of unit vector fields{X,Y}on¯M is given by
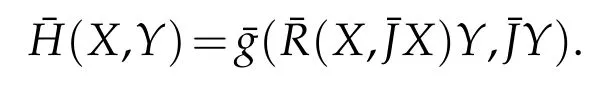
Definition 4.4.A GCR-lightlike submanifold M of an indefinite nearly K¨ahler manifold ¯M is said to be mixed geodesic if and only if h(X,Y)=0 for any X∈Γ(D)and Y∈Γ(D′).
Theorem 4.5.Let M be a mixed geodesic GCR-lightlike submanifold of an indefinite nearly K¨ahler manifold¯M with D0as a parallel distribution with respect to∇on M.Then¯H(X,Z)=0,for any X∈Γ(D0)and Z∈Γ(M2).
Proof.Let X,Y∈Γ(D0)and Z∈Γ(M2)then using the hypothesis that the distribution D0is parallel with respect to∇on M,we have
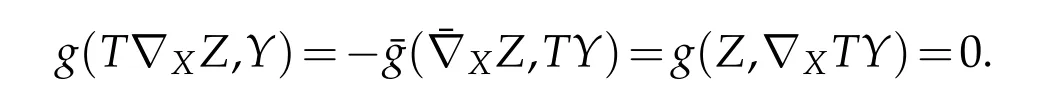
Hence the non degeneracy of the distribution D0implies that,T∇XZ=0,that is

for any Z∈Γ(M2).Now replacing Y by¯JX respectively in(2.11)and then taking inner product with¯JZ,for any X∈Γ(D0)and Z∈Γ(M2).Then by virtue of(2.10b),we get

Hence using that M is mixed totally geodesic with(4.9),the assertion follows.
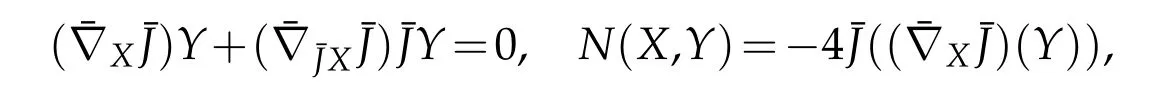
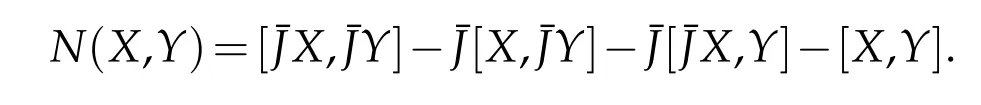

ofconstantholomorphic sectional curvature c.In order that it may admit a mixed geodesic GCR-lightlike submanifold M with parallel distribution D0,it is necessary that c≥0.


this implies that c≥0.



Thus the assertion follows.
Definition 4.5(see[6]).A lightlike submanifold(M,g)of a semi-Riemannian manifold(¯M,¯g)is said to be a totally umbilical in¯M if there is a smoothtransversal vector field H∈Γ(tr(TM))on M,called the transversal curvature vector field of M,such that h(X,Y)= H¯g(X,Y),for X,Y∈Γ(TM).Using(2.5),it is clear that M is a totally umbilical,if and only if,on each coordinate neighborhood u there exist smooth vector fields Hl∈Γ(ltr(TM))and Hs∈Γ(S(TM⊥))such that

for X,Y∈Γ(TM)and W∈Γ(S(TM⊥)).M is called totally geodesic if H=0,that is,if h(X,Y)=0.
Theorem 4.8(see[14]).Let M be a totally umbilical proper GCR-lightlike submanifold of an indefinite nearly K¨ahler manifold¯M.If D0defines a totally geodesic foliation in M then the induced connection∇is a metric connection.Moreover,hs=0.
Theorem 4.9.Let M be a totally umbilical GCR-lightlike submanifold of an indefinite nearly K¨ahler manifold of constant holomorphic sectional curvature c/=0 with the distribution D0defining a totally geodesic foliation in M.Then M is of constant curvature if and only if¯M is of constant type c.
Proof.Let X,Y∈Γ(D0⊕M2)be two orthonormal vectors such that g(X,Y)=g(X,¯JY)= 0.Since M is a totally umbilical GCR-lightlike submanifold with the distribution D0defining a totally geodesic foliation in M therefore using(4.3)and(4.5),the sectional curvature and holomorphic sectional curvature of M are given,respectively,by

and
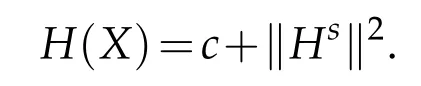
It follows that if¯M is of constant type c,then KM(X,Y)=c+‖Hs‖2.Hence M is a space of constant curvature c.
5 Null holomorphically flat GCR-lightlike submanifold

where V is an arbitrary non-null vector in π.
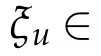
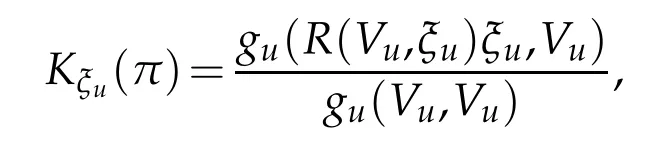
where Vuis an arbitrary non-null vector in π.
Let M be a GCR-lightlike submanifold of an indefinite nearly K¨ahler manifold of constant holomorphic sectional curvature c then using(4.2),the null sectional sectional
curvature of π with respect to ξ is given by
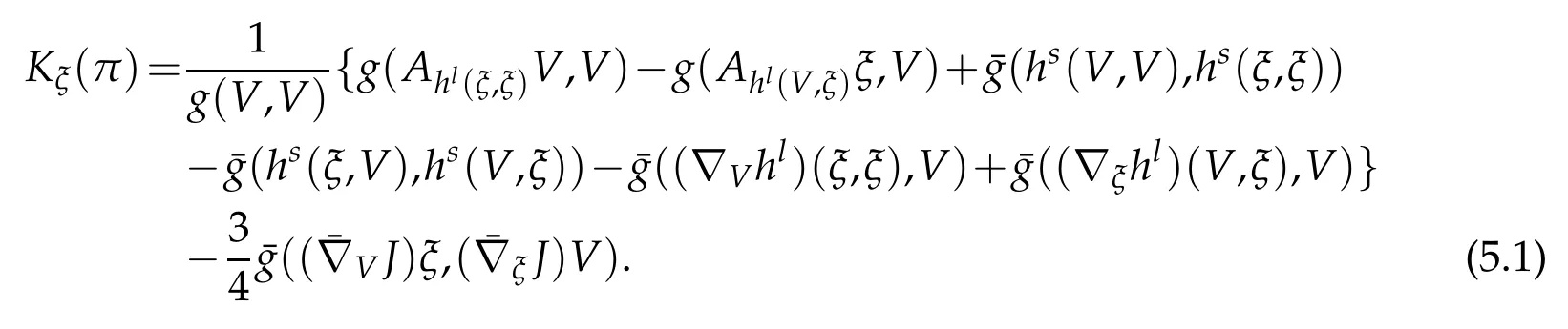
Then using(2.8),we obtain

We know that a plane π is called holomorphic if it remains invariant under the action of the almost complex structure¯J,that is,if π={Z,¯JZ}.The sectional curvature associated with the holomorphic plane is called the holomorphic sectional curvature,denoted by ¯H(π)and given by¯H(π)=¯R(Z,¯JZ,Z,¯JZ)/¯g(Z,Z)2.The holomorphic plane π={Z,¯JZ}is called null or degenerate if and only if Z is a null vector.A manifold(¯M,¯g,¯J)is called null holomorphically flat if the curvature tensor¯R satisfies,(see[2])
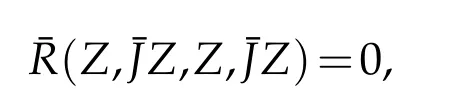
for all null vectors Z.Put¯g(¯R(X,Y)Z,W)=¯R(X,Y,Z,W),then from(5.2),we obtain


Thus(5.3)becomes

Let M be a totally umbilical lightlike submanifold then,we have h(¯Jξ,¯Jξ)=Hg(¯Jξ,¯Jξ)= Hg(ξ,ξ)=0 and h(ξ,¯Jξ)=Hg(ξ,¯Jξ)=0,for any ξ∈Γ(Rad(TM)).Thus from(5.4),we have the following theorem.
Theorem 5.1.Let M be a GCR-lightlike submanifold of an indefinite nearly K¨ahler manifold of constant holomorphic sectional curvature c.If M is totally umbilical lightlike submanifold then M is null holomorphically flat.
Moreover,from(5.4)it isclear thattheexpressionof R(ξ,¯Jξ,ξ,¯Jξ)is expressedinterms of screen second fundamental forms of M,thus GCR-lightlike submanifold M of an indefinite nearly K¨ahler manifold of constant holomorphic sectional curvature c is null holomorphically flat if M is totally geodesic.
[1]J.K.Beem and P.E.Ehrlich,Global Lorentzian Geometry,Marcel Dekker,New York,1981.
[2]A.Bonome,R.Castro,E.Garcia-Rio and L.M.Hervella,Null holomorphically flat indefinite almost Hermitian manifolds,Illinois J.Math.,39(1995),635-660.
[3]K.L.Duggal,CR structures and Lorentizian geometry,Acta Appl.Math.,7(1986),211-223.
[4]K.L.Duggal,Lorentzian geometry of CR submanifolds,Acta Appl.Math.,17(1989),171-193.
[5]K.L.Duggal and A.Bejancu,Lightlike submanifolds of semi-Riemannian manifolds and applications,Vol.364 of Mathematics and its Applications,Kluwer Academic Publishers,The Netherlands,1996.
[6]K.L.Duggal and D.H.Jin,Totally umbilical lightlike submanifolds,Kodai Math.J.,26(2003),49-68.
[7]K.L.Duggal andB.Sahin,ScreenCauchy-Riemannlightlike submanifolds,ActaMath.Hungar.,106(2005),125-153.
[8]K.L.Duggal and B.Sahin,Generalized Cauchy-Riemann lightlike submanifolds of K¨ahler manifolds,Acta Math.Hungar.,112(2006),107-130.
[9]A.Gray,Nearly K¨ahler manifolds,J.Differential Geom.,4(1970),283-309.
[10]S.I.Husain and S.Deshmukh,CR submanifolds of a nearly K¨ahler manifold,Indian J.Pure Appl.Math.,18(1987),979-990.
[11]Rakesh Kumar,Sangeet Kumar and R.K.Nagaich,GCR-lightlike product of indefinite K¨ahler manifolds,ISRN Geometry,(2011),Article ID 531281,13 pages.
[12]Sangeet Kumar,Rakesh Kumar and R.K.Nagaich,Characterization of holomorphic bisectional curvature of GCR-lightlike submanifolds,Adv.Math.Phys.,(2012),Article ID 356263,18 pages.
[13]Rakesh Kumar,Sangeet Kumar and R.K.Nagaich,Integrability of distributions in GCR-lightlike submanifolds of indefinite K¨ahler manifolds,Commun.Korean Math.Soc.,27(2012),591-602.
[14]Sangeet Kumar,Rakesh Kumar and R.K.Nagaich,GCR-lightlike submanifolds of indefinite nearly K¨ahler manifolds,Bull.Korean Math.Soc.,50(2013),1173-1192.
[15]K.Yano and M.Kon,Structures on Manifolds,Series in Pure Mathematics,Vol.3,World Scientific,Singapore,1984.
.Email addresses:rachna@pbi.ac.in(R.Rani),sp7maths@gmail.com(S.Kumar),dr rk37c@yahoo.co.in(R.Kumar),nagaich58rakesh@gmail.com(R.K.Nagaich)
28 June 2013;Accepted(in revised version)11 April 2016
 Analysis in Theory and Applications2016年2期
Analysis in Theory and Applications2016年2期
- Analysis in Theory and Applications的其它文章
- Multilinear Fractional Integrals and Commutators on Generalized Herz Spaces
- Commutators of Lipschitz Functions and Singular IntegralswithNon-Smooth KernelsonEuclideanSpaces
- Commutators ofLittlewood-PaleyOperatorsonHerz Spaces with Variable Exponent
- A Characterization of MRA Based Wavelet Frames Generated by the Walsh Polynomials
- Box Dimension of Weyl Fractional Integral of Continuous Functions with Bounded Variation
- On Growth of Polynomials with Restricted Zeros
