Variation of toughness and the length of paths and cycles

GAO Wei

（School of Information Science and Technology，Yunnan Normal University，Kunming 650092，China）

Variation of toughness and the length of paths and cycles

GAO Wei

（School of Information Science and Technology，Yunnan Normal University，Kunming 650092，China）

Computer networks are usually presented with graphs,where vertices represent sites and edges represent channels between sites.Toughness and its variation are used to measure the vulnerability of networks.For an undirected simple graph G,a variation of toughness is defined asif G is not complete，and τ（G）=∞if G is complete.This paper presents the bound of length of longest paths and cycles in τ-tough graphs.

graph；toughness；variation of toughness；longest path；longest cycle

Document code：AArticle ID：1672－0687（2016）01－0011－06

1　Introduction

We only consider simple undirected graphs in this paper.The notation and terminology used but undefined in this paper can be found in[1].Let l（P）and l（C）be the length of path P and cycle C，respectively.We denote p（G）and c（G）as the length of a longest path and of a longest cycle in a graph G，respectively.The notion of toughness was first introduced by chvátal in[2]：if G is a complete graph，t（G）=∞；if G is not complete，

where ω（G-S）is the number of connected components of G-S.A variation of toughness，introducedby Enomoto et al[3]，was defined as

if G is not complete，and τ（G）=∞if G is complete.In what follows，we always assume that τ>0.A graph G is called τ-tough if|S|≥τ·（ω（G-S）-1）establishes for each

The whole network can be modelled as a graph.Each site correspond to a vertex and each channel correspond to an edge in the graph.Toughness and variation of toughness usually regard as parameters to measure the strength of the network，and has widely used in communication networks and military network system.

For τ>0，k≥1 and n≥1，the notation（t，n）is denoted as the class of all τ-tough and k-connected graphs with n vertices.We define

Several papers contributed to the properties of τ（G）and t（G）.Enomoto[4]proved that if τ（G）≥k，k|G|iseven，and|G|≥k2-1，then G has a k-factor.Zhou[5]presented that a graph has a fractional k-factor if τ（G）>k where k=1，2.Liu[6]studied the relationship between toughness and fractional（g，f，n）-critical graphs and proved that G is a fractional（g，f，n）-critical graph if t（G）≥（（b2-1）（n+1））/a for a≤g（x）≤f（x）≤b with 1≤a≤b and b≥2.Zhou[7]learned the toughness condition for a fractional（k，m）-deleted graph.It is determined that G is a fractional（k，m）-deleted graph if t（G）≥k+（2m-1）/k.Other results on τ（G）and t（G）can refer to[8-11].

In this paper，we study the relationship between τ（G）and the length of longest path and cycle in a graph.It is highlighted that π（τ，n）and γ（τ，n）are bounded by the function of|V（G）|and τ.Some our main results depend heavily on the following lemma.

Lemma 1（Broersma[12]）Let G be a connected graph and P be a path in G with r as one of its end vertices. Then there exists a spanning tree T of G such that：

（a）T contains P，

（b）For every edge xy∈E（G），either x is on the（unique）path in T from y to r or y is on the path in T from x to r.

The organization of rest paper is as follows.In Section 2，we consider the relationship between τ-tough and the length of longest path in a graph.The lower bound of p（G）is determined in Theorem 1 and the upper bound of π（τ，n）with 0＜τ＜1 is presented in Theorem 2.In Section 3，we discuss the length of longest cycle in τ-tough graphs.The lower bound of c（G）and upper bound of γ（τ，n）（0＜τ＜1/2）are manifested in Theorem 3 and Theorem 4，respectively.

2　Long paths in τ-tough graphs

Our first result presents as follows concern the length of longest paths in τ-tough graphs.

Theorem 1Let G be a non-complete τ-tough graph with n vertices.Then,we have

Proof.Suppose that G is a non-complete τ-tough graph with n vertices.Let P=x0，…，xlbe a longest path in G，where l=p（G）.Since G is a τ-tough graph，we verify that G is connected and there exists a tree T just as in Lemma 1 with r=x0.Assume P′=x0，…，x「l/2is the subpath of P.

By the choice of P,there is no vertex in G-V（P′）connected to P′via a path in G with length not less thanl/2」.Specially,no path in T with length greater thanl/2」from a vertex outside P′to the path P′.For i≥0，let Li={x∈V（T），d（x，P′）=i}and Vi=L0∪L1∪…∪Li.We obtain L0=V0=V（P′）={x0，…，x「l/2}and V（G）=V（T）=Vl/2」. Hence，

By virtue of the characters of T，any two vertices in Li+1are in the different components of G-Vi（0≤i≤l/2」-1）. This implies（｜Li+1｜-1）≤｜Vi｜/τ.

Therefore，

Combining this with|V0|=「l/2+1，we get

We deduce the final result by taking logarithms.

Using the notation of π（τ，n），Theorem 1 can be expressed as

In this way，the following result is immediately obtained from Theorem 1. Corollary 1For fixed τ，we have as n→∞,andπ（τ，n）=∞.

The theorem stated as follows reveals that for 0＜τ≤1 the function log（n+τ）in Theorem 1 and Corollary 1 can’t replaced by a faster growing function with respect to n and τ.

Theorem 2The following inequalities hold：

Proof.Let m≥3,h≥1 and Tm-1，hbe the rooted tree in which each vertex with degree≥2 has degree m and each vertex with degree 1 is at distance h from the root.Let di=|{v∈V（Tm-1，h），d（v，v0）=i}|,where v0is the root of Tm-1，h.Then,we yield

Notice that after removing s≥1 vertices from Tm-1，hthe component number of the resulting graph is at most m+（s－1）（m－1）≤sm-s+1.Hence,Tm-1，his a 1/（m－1）-tough graph.Moreover,the length of longest path in Tm-1，his 2h.

Now,The following proof splits into two cases by the value of τ.

Case 10＜τ≤1/2

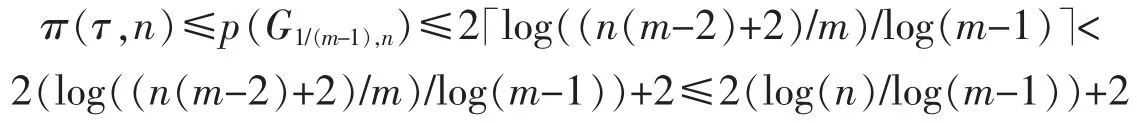
Case 21/2＜τ≤1

For h≥0,we recursively defineas below.Let

and

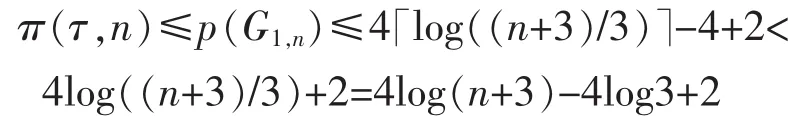
3　Long cycles in τ-tough graphs

Our first result in this section concern longest cycles of τ-tough graphs depends heavily on the following lemma.

Lemma 2（Dirac[13]）If G is a 2-connected graph with p（G）≥2,then

We infer the following corollary by substituting（c（G）2）/4 for p（G）in Theorem 1.

Corollary 2Let G be a non-complete τ-tough 2-connected graph with n vertices,then

The corollary stated below corresponding to Corollary 1 which is determined by Corollary 2.

Corollary 3For fixed τ,we have

and

Corollary 3 reveals that the function γ（τ，n）is bounded by a constant times.The conclusion stated as follows presents that such lower bound admits improvement.

Theorem 3Let G be a τ-tough 2-connected graph with n vertices.Then

Proof.Assume that G is a τ-tough 2-connected graph with n vertices and let C be a longest cycle in G. Let c=c（G）and suppose that G is non-complete.Define S0＝V（C）.For i≥1,Si，Pi，Li，Tiand the constant liare defined as follows.

For fixed Si⊂V（G）.We denote Pi+1as the set of paths of length at least 2 in G such that allinternal vertices belong to V（G）-Siand two end vertices in Si,and li+1be the length of a longest path in Pi+1.Then,let Li+1be a maximal collection of pairwise internally disjoint paths in Pi+1with length li+1.Next,we denote Ti+1as the set of internal vertices of the paths in Li+1and let Si+1=Si∪Ti+1.Since G is 2-connected and finite,there exist a minimal k satisfying Sk=V（G）.

Now,we deduce following characters for above notations on which the proof of main result may reckon.We omit the detail proofs.

Proposition 1l1≤c/2」.

Proposition 2li+1≤li-1 for 1≤i≤k-1.

Proposition 3For 1≤i≤k,no two paths in Lilie in the same component of G-Si-1.

Obviously,|S0|=|V（C）|=c.Furthermore,we get li≤c/2」+1-i by li+1≤li-1 and l1≤c/2」,which implies that k≤c/2」-1.Since the number of internal vertices on a path in Liis li-1,we infer

In view of Proposition 3,we deduce（|Li|-1）≤（｜Si-1｜/τ）.Thus,we have

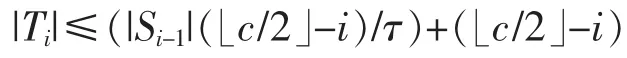
and

By virtue of|S0|=c,n=|V（G）|=|Sk|and k≤c/2」-1,we obtain

Finally,we derive the desired result by taking logarithms on both sides.□

Just as Theorem 2,we derive upper bounds for the function γ（τ，n）.

Theorem 4If 0＜τ≤1/2,then the function γ（τ，n）satisfies

Proof.Our proof relies on the graph which we constructed in the proof of Theorem 2.Assume that 0＜τ≤1/2.

Therefore,f（|S|）is strictly monotonic decreasing function with respect to|S|.Hence,min{f（|S|）}=f（∞）=1/（m-1）.

A 2-connected and τ-tough graphwith exactly n vertices could be constructed by deletinga suitable number of vertices of degree 2 on.A longest cycle incontains a longest path in-x and two edges incident with x.Therefore,in terms of p（Tm-1，h）=2h，we obtain

4　Conclusion

In this paper,we determine the bound of length of longest paths and cycles for τ-tough graphs.Since the variation of toughness is a parameter to measure the vulnerability of networks,our results have potential practical applications in computer networks and other scientific fields.

[1]BONDY J A，MUTRY U S R.Graph Theory[M].Spring：Berlin，2008.

[2]CHVÁTAL V.Tough graphs and hamiltonian circuits[J].Discrete Math，1973，5：215-228.

[3]ENOMOTO H，JACKSON B，KATERINIS P，et al.Toughness and the existence of k-factors[J].J Graph Theory，1985，9：87-95.

[4]ENOMOTO H，HAGITA M.Toughness and the existence of k-factor IV[J].Discrete Math，2010，216：111-120.

[5]ZHOU S.Toughness and the existence of fractional k-factors[J].Math Practice Theory（in Chinese），2006，36：255-260.

[6]LIU S.On toughness and fractional（g，f，n）-critical graphs[J].Inform Process Lett，2010，110：378-382.

[7]ZHOU S，SUN Z，YE H.A toughness condition for fractional（k，m）-deleted graphs[J].Inform Process Lett，2013，113：255-259.

[8]GAO W，LIANG L，XU T W，et al.Tight toughness condition for fractional（g，f，n）-critical graphs[J].J Korean Math Soc，2014，51（1）：55-65.

[9]GAO W，WANG W.A neighborhood union condition for fractional（k，m）-deleted graphs[J].Ars Combin，2014，CXIIIA：225-233.

[10]LIU S，CAI J S.Toughness and existence of fractional（g，f）-factors in graphs[J].Ars Combin，2009，93：305-311.

[11]ZHOU S.Toughness and the existence of Hamiltonian[a，b]-factors of graphs[J].Util Math，2013，90：187-197.

[12]BROERSMA H J，VAN DEN HEUVEL J，JUNG H A，et al.Long paths and cycles in toughgraphs[J].Graphs Combin，1993，9：3-17.

[13]DIRAC G A.Some theorems on abstract graphs[J].Proc London Math Soc，1952，2：69-81.

韧度的变量以及路和圈的长度

高炜
（云南师范大学信息学院，云南昆明650092）

一般地，计算机网络用图来表示，其中顶点表示站点，边表示站点之间的通道。韧度和它的变量用来衡量网络的易受攻击性。对于无向简单图G，韧度的变量定义为若G不是完全图；τ（G）＝∞若G是完全图。文中给出τ-韧度图中最长路和最长圈的长度的界。

图；韧度；韧度的变量；最长路；最长圈

2015－02－05

国家自然科学基金资助项目（11401519）

高炜（1981－），男，浙江绍兴人，副教授，博士，研究方向：机器学习和图论。

O157.5MR（2000）Subject Classification：90B10

责任编辑：艾淑艳