可求和布尔函数的性质

曾利全，许道云

(1.贵州大学数学系，贵州贵阳　550025；2.贵州大学计算机科学系，贵州贵阳　550025)

可求和布尔函数的性质

曾利全1，许道云2*

(1.贵州大学数学系，贵州贵阳550025；2.贵州大学计算机科学系，贵州贵阳550025)

可求和布尔函数是临界布尔函数判定理论中比较重要的内容之一。该类函数有一个参数k，k表示布尔函数存在k个成真点X1，X2，…Xk和k个成假点Y1，Y2，…Yk，并且它们的和相等。本文主要研究了n元2-可求和布尔函数和n元3-可求和布尔函数的基本性质。

临界布尔函数；2-可求和布尔函数；3-可求和布尔函数

一个n元布尔函数f(X)是指:f:{0，1}n→{0，1}，其中n为正整数，Bn为n维{0，1}向量。对于每一个X＝(x1，x2，…，xn)∈Bn，其中，xi∈ {0，1}，i＝1，2，…，n。若X为成真点，则f(X)＝1，若X为成假点，则f(X)＝0。用T(f)表示f(X)的成真点集，F(f)为f(X)的成假点集。n元布尔函数f(X)称为k-可求和布尔函数[1]，是指对于r布尔函数f(X)存在r个错误点X1，X2，…Xr和 r个正确点 Y1，Y2，…Yr，使得成立。n元布尔函数f(X)是否为可求和布尔函数是判定该函数为临界布尔函数的充要条件。它是一个判定n元布尔函数f(X)是否为临界布尔函数的有效方法。自从上世纪五六十年代由Paul和McCluskey[2]首次提出了临界布尔函数的概念之后，国内外有许多的科学家对其进行了深入的研究。在文献[3]中，Winder和Margo对临界布尔函数进行了重新命名，同时得到了很多重要的结果，主要工作是找出了在含有7个布尔变量的布尔函数中存在的所有临界布尔函数，以及应用simplex-方法来判定临界布尔函数，这类布尔函数的推广和不断被人们接受则是在Winder[4]、Moraga[5]和Gamelan[6]三位学者不断研究和努力之下实现的，他们证明了权值和变量之间的关系，临界函数和它的对偶函数之间的关系，真假值点之间的关系。近几年，研究者发现单调布尔函数可以对单调的线性临界布尔函数进行估计[7]，利用布尔函数是否可求和[8]、把给定的逻辑转化为临界门的方法[9]等等都可以对临界布尔函数进行判定。接着，研究者们还发现，对正则函数的研究有利于临界布尔函数的确认，正则函数的判定算法对临界布尔函数的判定也是一种有效的手段。通常情况下，我们对临界布尔函数性质的研究是建立在临界布尔函数判定的基础上，故研究临界布尔函数的性质的关键首先是研究临界布尔函数的判定。

目前，对临界布尔函数性质的研究也很多，比如临界布尔函数f(X)的分割和真假值之间的关系，布尔函数和临界布尔函数表达式之间的关系，和权值之间的关系，单调性等等性质，由于它真假值分布的特殊性，即真假值被一个超平面分割[10]，这使得它作为一种特殊的模型被广泛的应用在电子信息工程、人工神经网络、可靠性原理还有博弈论等领域。因此研究临界布尔函数的判定方法也具有重要的现实意义。

1985年Peled和 Simeone[11]两位学者研究发现:在正的布尔函数中，对于完全DNF是否为临界布尔函数的判定时间为O(n7m5)，其中，n是布尔函数元素的个数，m是主要蕴含项被检测的个数。而这唯一的判定算法可以判定的布尔函数的范围较窄，近年来，对临界布尔函数的判定算法研究较少，那么从布尔函数是否可求和判定这个函数是否为临界布尔函数则成为了一个较重要的方法。

本文的工作主要是研究n元布尔函数f(X)为2-可求和、3-可求和布尔函数的性质。目的在于让我们对可求和函数有更深刻的理解，以便设计出更好的判定临界布尔函数的算法。为了研究n元布尔函数f(X)为2-可求和、3-可求和布尔函数的一些性质，接下来，我们首先介绍一些相关的概念和术语。

1　基础知识

n元布尔函数f(X)，它的布尔变量xi在表达式中可以表示成xi或。对于n元布尔函数f(X)的每个子式既可以表示成合取式，也可以表示成析取式。其中:

我们知道，每一个n元布尔函数f(X)都可以写成如下的一个析取标准式(DNF):

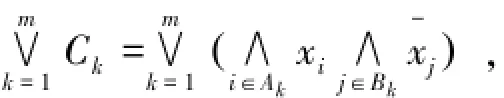
其中每个Ck(k＝1，2，…，m)是一个合取式，我们把Ck(k＝1，2，…，m)叫做析取标准式(DNF)的子式。或者是一个合取标准式(CNF)。形如:

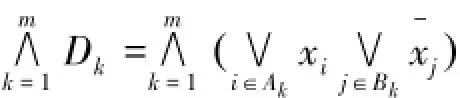
其中每个Dk(k＝1，2，…，m)是一个析取式，我们把Dk(k＝1，2，…，m)叫做合取标准式(CNF)的子式。并且在n元布尔函数f(X)中，对于任意布尔变量xi，它的否定为，反之对于的否定则为xi，因为布尔函数的基本性质有

注:在本文中提到的子式间的不同元素，不仅是指下标不同的元素，而且还包括xi与或者是元素xi在一个子式出现而在另一个子式没有出现也为不同元素。而相同元素是指xi与xi，或者是与，其中i＝1，2，…，n。

引理1.1[12].每个n元布尔函数f(X)都可以表示成一个合取标准式(CNF)或者是一个析取标准式(DNF)。

注:本文出现的布尔函数都是以析取标准式的形式出现的。在DNF中，对任意的k＝1，2，…，m，…Xr和r个成假点 Y1，Y2，…Yr，使得

定义1.2.临界布尔函数f(X)是布尔函数中的一种特殊函数，从几何学的角度来讲，它的特殊之处在于这类布尔函数的真假值被一个超平面分开。即:

f(x1，x2，…xn)＝0当且仅当

f(x1，x2，…xn)＝1当且仅当

其中f是一个布尔函数，w1，w2，…wn是n个权值，t是临界函数的临界值。

引理1.2[12].对于n元布尔函数f(X)若为临界布尔函数当且仅当f(X)为不可求和函数。

2　2-可求和布尔函数的性质

接下来，首先引入k-可求和布尔函数以及临界布尔函数的概念。

定义1.1.假设f(X)是一个n元布尔函数，X＝(x1，x2，…，xn)是赋值指派，若f(X)＝1，则称X为成真点。若f(X)＝0，则称X为成假点。一个布尔函数 f(X)称为 k-可求和函数，是指对于 r∈{2，3，…，k} ，布尔函数存在r个成真点X1，X2，其中从2-可求和布尔函数的定义可以看出，选取的两个成真点或者两个成假点是由n元布尔函数f(X)中的两个子式决定的。所以研究2-可求和布尔函数只需讨论决定布尔函数为2-可求和布尔函数的两个子式所满足的条件。

下面将给出对于n元2-可求和布尔函数f(X)的几个重要性质，即表达式中存在形如:的两个子式，其中A1，B1和A2，B2为对应子式中元素的下标集，并且都是正整数集。

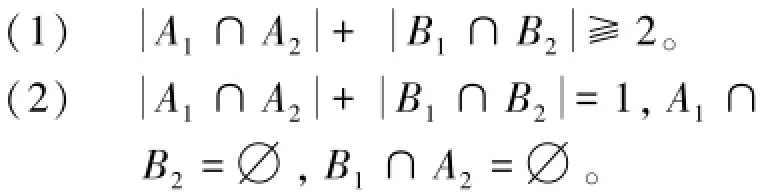
(5)A1∩A2＝∅，B1∩B2＝∅，并且除相同元素外，每个子式至少有2个元素不同与另一个子式。

证明:对于n元布尔函数f(X)，元素xi在每个子式中出现的形式为xi或，其中i＝1，2，…，n。若元素xi在子式中以xi出现，令xi＝1。若元素xi在子式中以出现，令xi＝0。若元素xi没有在子式中出现，令xi＝0或xi＝1。则f(X)的每个子式都可以得到与之对应且长度为n的成真点。

由于(1)中的两个子式得到的两个成真点可以用2×n矩阵表示，其中矩阵每一行的元素由这两个子式得到的成真点组成。因此2×n矩阵中每一列的元素可能是01，10，00，11，要找到两个成真点对应的两个成假点，是针对2×n矩阵列中元素是01，或10位置的调换。列中元素为00或11，调换不会使两个成真点变为成假点。因为(1)的两个子式满足所以在矩阵中至少有两列为01，或10。只需调整每列中0 与1的位置，则成真点就变为成假点。因为只是同一列中元素位置的调换，所以不影响每一列元素相加的结果。通过上面的步骤就可以得到与(1)的两个成真点相对应的两个成假点。

由于(2)得到的2×n矩阵中，每一列中的元素可能是 01，10，00。(2)的两个子式满足若变量xi在其中一个子式中以xi的形式出现，在另一个子式中没有出现，在另一个子式的成真点中令xi＝0；若变量xi在其中一个子式中以的形式出现，在另一个子式中没有出现，则在另一个子式的成真点中令xi＝1；若变量xi在两个子式中都没有出现，则这两个子式的成真点中令xi＝0；在两个成真点得到的2×n矩阵中至少有3列中的元素为01或10。同理，调整每列中0与1的位置就可以得到对应的成假点。

由于(3)是在(2)的基础上增加了相同元素，两个成真点得到的2×n矩阵中，列中元素可能是10，01，00，11。因为(3)的两个子式满足:除相同元素外，每个子式至少有2个元素不同与另一个子式。在2×n矩阵中，至少有3列为01或10。同理，调整每列中0 与1的位置就可以得到对应的成假点。

由于(4)得到的2×n矩阵中，每一列中的元素可能是01，10，00。由，可知，在2×n矩阵中至少有4列中的元素为01或10。调整每列中0与1的位置就可以得到对应的成假点。

由于(5)是在(4)的基础上增加了相同元素，(5)的两个子式满足:A1∩A2＝∅，B1∩B2＝∅，并且除相同元素外，每个子式至少有2个元素不同与另一个子式。可知在2×n矩阵中至少有4列中的元素为01或10。调整每列中0与1的位置就可以得到对应的成假点。

所以，对于n元2-可求和布尔函数f(X)，它的表达式中存在两个子式满足性质3.1。

3　3-可求和函数的性质

判定n元布尔函数f(X)为3-可求和布尔函数，前提必须满足该n元布尔函数f(X)为2-可求和布尔函数。若f(X)为2-可求和布尔函数，需要存在3个成真点Xi，Xj，Xk，和三个成假点使得成立，则f(X)为3-可求和布尔函数。由于f(X)为3-可求和布尔函数的前提是该函数为2-可求和布尔函数，而对于n 元2-可求和布尔函数f(X)，它的表达式中存在两个子式决定该函数为2-可求和函数。所以，n元2-可求和布尔函数f(X)若为3-可求和布尔函数，其表达式中必定存在第三个子式决定该函数为3-可求和布尔函数。经研究发现，对于n元3-可求和布尔函数f(X)，该布尔函数中元素的个数n≧4，并且f(X)中子式的个数至少为3个。

下面将给出对于n元3-可求和布尔函数f(X)的几个重要性质。即表达式中除含有决定2-可求和的两个子式外，还存在形如的一个子式，其中Ai，Bi为该子式的下标集，i＝3，4，…，n。即该子式不同于2-可求和得到的两个子式。

性质3.1在性质2.1的(1)、(2)、(3)基础上，若n元2-可求和布尔函数f(X)为3-可求和布尔函数，则f(X)存在形如:的一个子式，并且子式的下标集Ai，Bi满足下列情况之一:

情况1、若该子式不含有性质2.1(1)、(2)、 (3)得到的两个子式中的相同元素，当2时，该子式至少含有一个元素不同与性质2.1 (1)、(2)、(3)得到的两个子式中的元素。当时，则为3-可求和布尔函数。

情况2、若该子式含有性质2.1(1)、(2)、(3)得到的两个子式中的相同元素，假设该子式含有a个元素，其中有b个元素为性质2.1(1)、(2)、(3)得到的两个子式中的相同元素，则该子式除性质1得到的两个子式中的相同元素外至少含有两个元素。当a-b＝2，则至少含有一个元素不同于前两个子式。当a-b≧3，则为3-可求和布尔函数。

证明:对于n元布尔函数2.1(1)、(2)、(3)得到的两个子式，若元素xi在子式中以xi出现，令xi＝1。若元素xi在子式中以出现，令xi＝0。

情况2只是假设第三个子式含有性质2.1(1)、(2)、(3)的两个子式中的相同元素，同理可以按照情况1的方法得到对应的成假点。所以对于满足性质2.1(1)、(2)、(3)的n元2-可求和布尔函数f(X)，若f(X)为3-可求和布尔函数，则存在第三个子式满足性质3.1。

性质3.2在性质2.1的(4)基础上，若n元2-可求和布尔函数f(X)为3-可求和布尔函数，则f(X)存在形如:的一个子式，并且子式的下标集Ai，Bi满足下列情况之一:

证明:对于n元布尔函数f(X)，若元素xi在子式中以xi出现，令xi＝1。若元素xi在子式中以出现，令xi＝0。若元素xi在子式中没有出现，令xi＝0。则f(X)的每个子式都可以得到与之对应且长度为n的正确点。对于3-可求和布尔函数的3个对应子式，它们的成真点组成一个3×n矩阵。

所以，对于满足性质2.1(4)的n元2-可求和布尔函数f(X)，若f(X)为3-可求和布尔函数，则存在第三个子式满足性质3.2。

性质3.3在性质2.1的(5)基础上，若n元2-可求和布尔函数f(X)为3-可求和布尔函数，则f(X)存在形如:的一个子式，若该子式不含有性质2.1(5)得到的两个子式中的相同元素，则与性质3.2的情况2相同。若该子式含有性质2.1(5)得到的两个子式中的相同元素，假设这三个子式含有p个相同元素，则并且子式的下标集Ai，Bi满足下列情况之一:

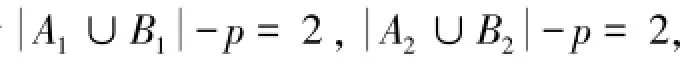
当时，该子式除三个子式中的相同元素外，至少含有一个元素不同于性质2.1(5)得到的两个子式中的元素。当时，则为3-可求和布尔函数。

证明:性质3.3是在性质3.2的基础上增加了相同元素。同理，用性质3.2的方法可以得出性质4.3为3-可求和布尔函数。

4　结束语

本文从n元2-可求和布尔函数f(X)的定义出发，研究了n元2-可求和布尔函数f(X)的几个重要性质。即对于n元布尔函数f(X)，若该布尔函数为2-可求和布尔函数，则在f(X)的表达式中存在两个子式使得该函数为2-可求和布尔函数，本文得出了这两个子式所具备的性质。在n元布尔函数f(X)为2-可求和布尔函数的基础上，本文还研究了n元3-可求和布尔函数f(X)的几个重要性质。若该函数为3-可求和布尔函数，则f(X)

在2-可求和的基础上，它的表达式中存在第三个子式使得2-可求和布尔函数f(X)为3-可求和布尔函数，本文得出了第三个子式所具备的性质。

[1]Winder R O.Threshold Logic[D].Princeton:Princeton University，1962.

[2]Paul M C，McCluskey E J.Boolean functions realizable with single threshold devices[J].Proc.IRE，1960，07(5):1335-1337.

[3]Winder R O.Single stage threshold logic.Switching Circuit Theory and Logical Design，1961.SWCT 1961.Proceedings of the Second Annual Symposium on[J].IEEE，1961，12(3):321-332.

[4]Winder R O.More about threshold logic.2013 IEEE 54th Annual Symposium on Foundations of Computer Science[J].IEEE，1961 (3):55-64.

[5]Winder R O.Properties of threshold functions[J].IEEE Transactions on Electronic Computers，1965(14):252–254.

[6]Moraga S，Toda I，Takes S.Theory of majority decision elements [J].Franklin Institute，1961，03(5):376-418.

[7]Gamelan I J.The functional behavior of majority(threshold)elements[D].New York:Syracuse University，1961，06.

[8]Rocco A.Department of Computer Science[J].Columbia University，2003，07(11):181–187.

[9]Eater T，Makino K，Grotto G.Recognizing renewable generalized propositional Horn formulas is NP-complete[J].Discrete Applied Mathematics，1995，04(1):23–31.

[10]Ekin O，Foldes S.Identification of Threshold Functions and Synthesis of Threshold Networks[J].IEEE Transactions on Computer -aided Design of Integrated Circuits and Systems，2011.03(5):665-677.

[11]Peled U N，Simeone B.Polynomial-time algorithms for regular set -covering and threshold synthesis[J]，Discrete Applied Mathematics，1985，09(1):57–69.

[12]Yves Crama，Peter L.Hammer.Boolean functions Theory，Algorithms，and Applications[M].New York:Cambridge University press，2011.

(责任编辑:王先桃)

The Properties of 2-Summable Boolean Function and 3-Summable Boolean Function

ZENG Liquan1，XU Daoyun2*
(1.Department of Mathematics，Guizhou University，Guiyang 550025，China；2.Department of Computer Science，Guizhou University，Guiyang 550025，China)

One of the most important theorem in recognition of threshold function is the k-asummable Boolean function for all k≥2，where k is the number of true point of the Boolean function，say X1，X2，…Xk，and the number of false point of the Boolean function，say，Y1，Y2，…Yk，such that.It is shown that the basic properties of 2-summable Boolean function and 3-summable Boolean function.

threshold function；2-summable function；3-summable function

TP301

A

1000-5269(2016)01-0046-06DOI:10.15958/j.cnki.gdxbzrb.2016.01.12

2015-11-23

国家自然科学基金项目资助(61262006)

曾利全(1988-)，男，在读硕士，研究方向:计算复杂性，Email:849962907＠qq.com.

许道云，Email:dyxu＠gzu.edu.cn.