立体几何问题的解答中图形的构造技巧

☉河南大学附属中学　（23中）张一廿

立体几何问题的解答中图形的构造技巧

☉河南大学附属中学（23中）张一廿

在立体几何客观题中常涉及一些求距离、角度、面积、体积问题，但与这些问题相关的点、线、面的位置关系并没有明确给出，需要我们结合题目条件准确构造出这些对象所在的位置.那么具体问题中应如何构造，这是问题能否顺利求解的关键.本文以2016年一道高考题为引例，就其中所涉及的构造思想进行分析.

引例（2016全国I卷）平面α过正方体ABCD-A1B1C1D1的顶点A，α∥平面CB1D1，α∩平面ABCD=m，α∩平面ABB1A1=n，则m，n所成角的正弦值为（）

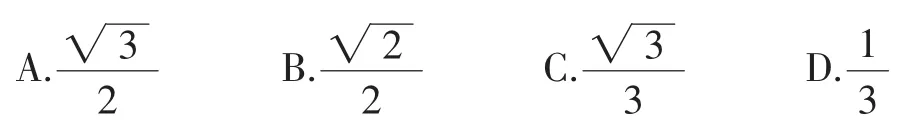
题目条件中面α的位置没有明确给出，因此涉及的两条线m，n的位置也不确定.那么应如何构造出过顶点A且与面CB1D1平行的平面α，是问题求解的关键.下面从两种视角来构造平面α，来实现问题的简洁求解.

解法1：如图1，延长D1A1至点D2，使A1D2=D1A1.延长B1A1至点B2，使A1B2=B1A1，连接B2D1，B2D2，AB2，AD2，B1D2，

易知B2D2∥=B1D1，AB2

∥=CD1，AD2

∥=CB1，所以平面AB2D2∥面B1CD1，所以面AB2D2即为题目中的面α，AB2即为直线m所在的位置，B2D2即为直线n所在的位置.

又因为CD1，CB1，B1D1均为正方体ABCD-A1B1C1D1的面对角线，所以CD1=CB1=B1D1，所以B2D2=AB2=AD2，即△AB2D2为等边三角形，则m，n所成角即为AB2与B2D2的夹角，其大小为，故其正弦值为

图1　

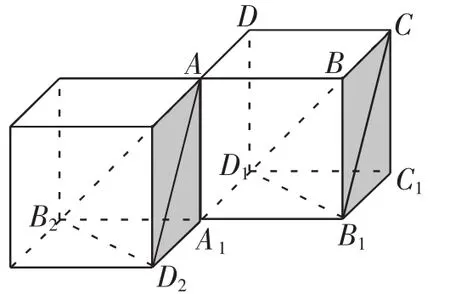
解法2：构造与正方体ABCD-A1B1C1D1相连的正方体，如图2所示，则条件中所求的各对象直观地展现在我们面前，易知面AB2D2即为已知条件中的α，则m，n的位置相应地确定了.故可直接得出正确答案.

点评：本题的求解关键是根据题目特征，找到所求的面，进而将所求关系明确化，使问题简洁获解.

除此之外，在某些问题中，与题目相关的点、线、体等条件的确定是问题顺利求解的重要保证，下面举例说明.

一、构造定点

例1如图3所示，正方体ABCDA1B1C1D1的棱长为1，BD∩AC=O，M是线段D1O上的动点，过点M做平面ACD1的垂线交平面A1B1C1D1于点N，则点N到点A距离的最小值为（）

图3　

解析：本题求动点N到定点A的距离的最小值，关键是确定点N所在的位置.

如图4，连接B1D1，根据题目条件易知平面ACD1⊥平面BDD1B1，而NM⊥平面ACD1，即NM⊥OD1，所以NM的面BDD1B1内，所以点N的轨迹为面BDD1B1与面A1B1C1D1的交线B1D1上.连接AB，易知△AB1D1为等腰三角形，故当N为B1D1的中点时，NA的距离最小，易求得最小值为.故选B.

图4　

点评：本题求解的关键是确定点N所在的位置，即点N在线段B1D1上运动，进而将问题转化为点到线的最短距离，易知AN⊥B1D1时，距离最小.

二、构造定线

例2在边长为2的正方体ABCD—A1B1C1D1中，E为BC的中点，点M在底面ABCD上移动，且满足B1M⊥D1E，则线段B1M长度的最大值为（）

解析：因为点M为动点，但B1M⊥D1E，故B1M在与D1E垂直的平面内.

如图5，设CC1的中点为N，因为B1N与BC均在面BCC1B1内，所以B1N与BC所在的直线相交，设交点为S，连接AS.又因为点S在ABCD所在的平面内，所以AS与CD相交，设交点为O.

连接AB1，由三垂线定理易证D1E⊥AB1.

连接C1E，易证B1N⊥C1E，而C1D1⊥B1N，

所以B1N⊥平面C1D1E，所以B1N⊥D1E.

综上，D1E⊥平面AB1S，即点M在线段AO上.

又因为△SCN～△SBB1，△SOC～△SAB，

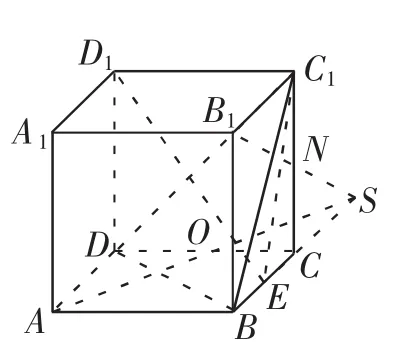
图5　

评析：本题的求解关键是确定动点M所在的定线的位置.对于动态问题的解答要善于把握其中不变的因素，如本题中点M为面ABCD内的动点，但B1M⊥D1E，因此B1M在一个与D1E垂直的定面上，找到这个定面即可顺利找到动点M所在的直线.另外题目中若涉及一条动直线与已知平面平行，则动直线在与已知面平行的定面内.解题中只要抓住这些动态问题中的确定因素，就可顺利找到问题的切入点.

三、构造定面

例3如图6所示，在正方体ABCD-A1B1C1D1中，点E是边BC的中点，动点P在直线BD1（除B，D1两点）上运动的过程中，平面DEP可能经过的顶点是_______（写出满足条件的所有顶点）.

解析：由题意知，平面DEP过点D.

若平面DEP过点A1，如图7所示作平面A1DE，与BB1交于点F，DF与BD1在平面BDD1B1内，则DF与BD1的交点即为点P，故平面DEP过点A1.

若平面DEP过点B1，如图8所示作平面B1DE，与A1D1交于点F，DB1与BD1在平面BDD1B1内，则DB1与BD1的交点即为点P，故面DEP过点D1.

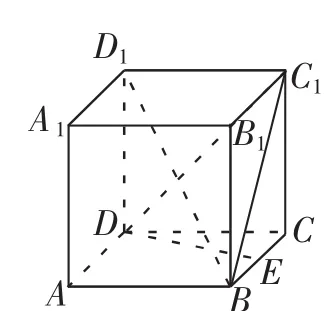
图6　

若面DEP过点C1，如图9所示作面C1DE，由图易知DC1与CD1在面CDD1C1内，设DC1与CD1交于点F，则易知点F为CD1的中点.连接EF，所以EF为三角形BCD1的中位线，所以EF平行于BD1，即面DEC1与BD1没有交点，所以满足条件的点P不存在，所以面DEP不经过点C1.

综上所述，正确答案为A1，B1，D.

图7　

图8　

图9　

点评：本题若直接作面DEP，看其过哪些顶点，则陷入误区.转换问题求解视角，即选择某个顶点，结合D、E构造平面，只要保证所作平面与BD1相交，则该顶点符合要求.

四、构造定体

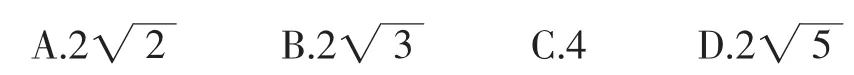
解析：根据题目条件可构造符合条件的长方体，通过长方体的体对角线在三个面上的投影来实现对问题的解答，即利用长方体的体对角线和面对角线列出方程组，转化为a和b的关系，再根据a和b关系确定最大值.具体解答过程如下：

根据题意，如图10所示，设长方体的长、宽、高分别为m、n、k，则

图10　

所以（a2-1）+（b2-1）=6，即a2+b2=8.

所以（a+b）2=a2+2ab+b2=8+2ab≤8+a2+b2=16，

即a+b≤4，当且仅当a=b=2时取等号.所以当a=b=2时，a+b取最大值4.

评析：对于某些空间几何体问题中，如果涉及几何体的三视图，常用的解题策略是根据三视图，构造相应的特殊几何体，如长方体、正方体等，能给问题的解决带来便利.本题解答中通过联想、构造，将问题转化为长方体的一条体对角线在三个面上的投影问题，降低了难度，使问题得到顺利解决.