三人模糊联盟合作博弈的最小核心解*

卜 红，南江霞

(桂林电子科技大学 数学与计算科学学院，广西高校数据分析与计算重点实验室，广西 桂林 541004)

三人模糊联盟合作博弈的最小核心解*

卜 红，南江霞

(桂林电子科技大学 数学与计算科学学院，广西高校数据分析与计算重点实验室，广西 桂林 541004)

研究了联盟是模糊的合作博弈.利用多维线性扩展的方法定义了模糊联盟最小核心解，并推导出三人模糊联盟合作博弈最小核心的计算公式.研究结果发现，多维线性扩展的模糊联盟合作博弈最小核心解是对清晰联盟合作博弈最小核心解的扩展.最后给出三人模糊联盟合作博弈的一个具体事例，证明了此方法的有效性和适用性.

运筹学；模糊联盟最小核心解；多维线性扩展方法

1 引 言

合作博弈是博弈论重要的分支，已经在各个领域得到广泛应用.但现实生活中，如(李登峰(2003)，Branzei and Dimitrov et al(2005)，Bumariu and Kroupa (2009)，李登峰(2012)，LI(2012)， Branzei and Dimitrov (2008) ) 文中所提到的环境的不确定性、可支配资源的有限性等原因[1-6]，局中人常以一种参与度去参与联盟，因此， Aubin(1974)首次提出了模糊联盟的概念[7]，即局中人在参与合作时，参与程度可以不同，用[0,1]间的一个实数表示，由于其更符合人们的心理和实际问题，模糊联盟合作博弈的理论和应用引起了许多国内外研究者的关注，成为合作博弈理论的重要组成部分和研究热点之一.许多研究者对模糊联盟合作博弈进行了深入的研究，如孙红霞(2010)首先拓展了 Owen 联盟值在经典意义下满足的 5 个公理，利用 Choquet 积分给出了基于联盟结构的模糊合作博弈的 Owen 联盟值，即模糊 Owen联盟值的具体形式，并证明该联盟值满足新定义的 5 个公理[8].占家权和张强(2010) 提出一类具有特殊结构的模糊合作博弈的资源分配方法，而且其方法可以保证所有局中人支付之和最大, 从而解决了模糊合作博弈中会形成什么样的模糊联盟结构的问题[9].黄武军等(2010)研究了拟阵约束下TU模糊合作博弈的Banzhaf-Colema值[10].Owen(1972)等引入了多维线性扩展方法，用于大规模清晰合作博弈的Shapley值计算，并利用此方法对经典合作博弈进行拓展，提出了多维线性扩展的模糊联盟合作博弈[11].Meng(2010)等对具有多维线性扩展形式的模糊联盟合作博弈Shapley值进行研究，证明了Shapley值的存在性和唯一性,并给出了解析表达式[12].孟凡永(2012)提出了基于多维线性扩展模糊联盟合作博弈的Banzhaf值，讨论了其性质和公理化方法[12].综上所述目前，该研究的重要分支就是利用多维线性扩展方法对清晰联盟合作博弈下的支付函数进行模糊拓展，并提出基于多维线性扩展的模糊联盟合作博弈分配方案.从文献中看基于多维线性扩展的模糊联盟合作博弈Shapley值和Banzhaf值等都有深入的研究，成果较多，但对于最小核心的研究很少.最小核心弥补了核心可能是空集的缺陷，另外三人博弈在现实生活中很普遍，很多联盟都是产、供、销三方联盟，因此研究三人模糊合作博弈最小核心具有一定的理论价值和应用价值.文中探讨了基于多维线性扩展的三人模糊联盟合作博弈的最小核心.利用多维线性扩展方法对经典清晰联盟合作博弈最小核心进行模糊拓展，定义了基于多维线性扩展的模糊联盟合作博弈的核心、强ε-核心和最小核心，并给出最小核心的一些性质.最后通过算例来说明基于多维线性扩展的模糊联盟合作博弈的最小核心的有效性和实用性.

2 模糊联盟合作博弈的最小核心的基本概念

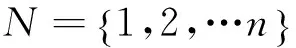
，实值支付函数v(SN)表示为模糊联盟SN合作时可期望获取的支付，满足v(eφ)=0.当(SN)i只取0和1时模糊联盟SN就退化为清晰联盟，相应的模糊联盟合作博弈就退化成清晰联盟合作博弈.

定义1.1(孟凡永等(2010)[13]) 令v∈G(N)，给定模糊联盟SN∈L(N)，基于多维线性扩展模糊联盟合作对策的支付函数为

-(ST)i))v0(P)，(T⊆N)，

则称v是关于v0基于多维线性扩展的模糊联盟合作博弈.其中v0为清晰联盟合作博弈的特征函数，即v0:N→R且满足v0(φ)=0.记Gm(N)为基于多维线性扩展的模糊联盟合作博弈的集合.

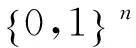
定义1.2 (汪贤裕等(2008)[14]) 设v∈Gm(N)和SN∈L(N)，v的模糊核心C(SN,v)可表示为

模糊核心是所有局中人都能接受的分配方案组成的集合，这是因为任意的模糊子联盟中的所有局中人所获得支付之和都不少于其联盟所得的支付.

定义1.3 设v∈Gm(N)和SN∈L(N)，ε是一个实数.非空的预转归集称为他的强ε-核心，记为Cε(SN,v)：

定义1.4 设v∈Gm(N)和SN∈L(N)，ε0是使得Cε(SN,v)≠φ的最小ε，称Cε0(SN,v)为Gm(N)的最小核心，记为LC.

根据模糊联盟合作博弈最小核心的定义，对模糊联盟合作博弈的最小ε-核心LC，可将经典合作博弈的ε*的求解方式推广到模糊联盟合作博弈ε*的求解，即：可用下面线性规划求解．

(1)

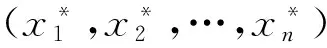
3 计算三人模糊联盟合作博弈的最小核心

三人模糊合作博弈在现实生活中很普遍，很多联盟都是产、供、销三方联盟，根据定义1.1和定义1.4，下面将给出三人模糊联盟合作博弈最小核心的计算公式.

定理2.1 三人模糊联盟合作博弈的最小核心的计算公式为：

Cε0=

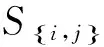
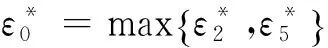
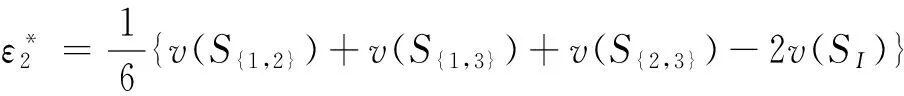
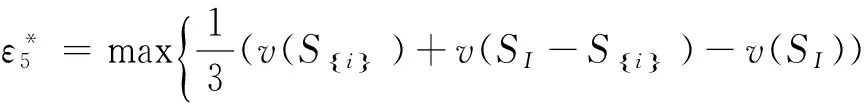
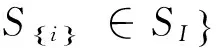
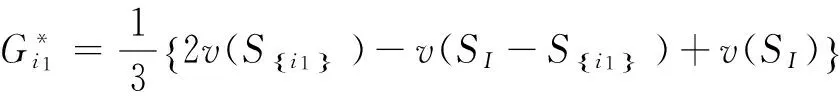
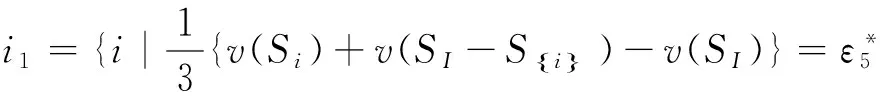
Si∈SI},

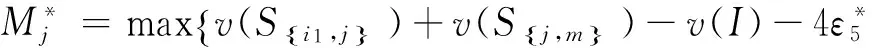
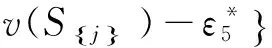
min z=ε*

(2)

(3)

(4)

(5)

(6)

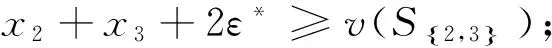
(7)

x1+x2+x3=v(SI)．

(8)

由式(2)得

(9)

由式(7)和式(8)可得

(10)

由式(5)，式(6)和式(8)可得

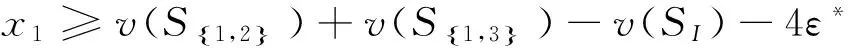
(11)

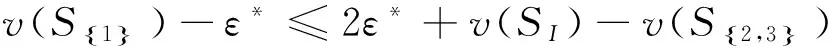
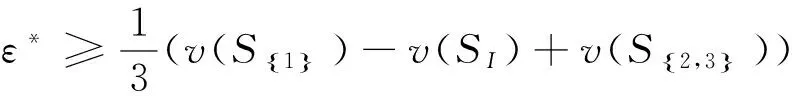
(12)

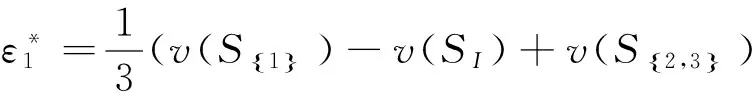
由式(10)和式(11)可得

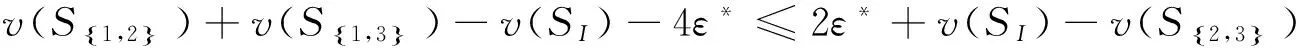
求解ε*可得

(13)

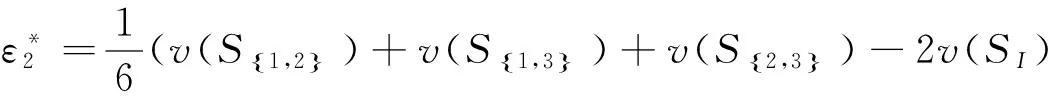
由式(12)和式(13)得

同理若x2有解则求解ε*可得

(14)

(15)

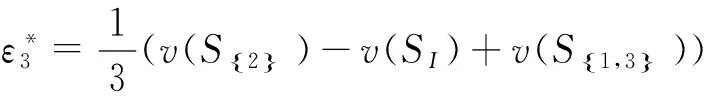
同理若x3有解则求解ε*可得

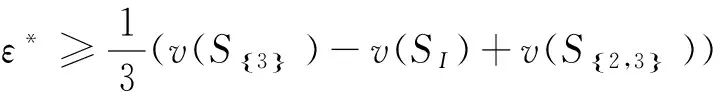
(16)

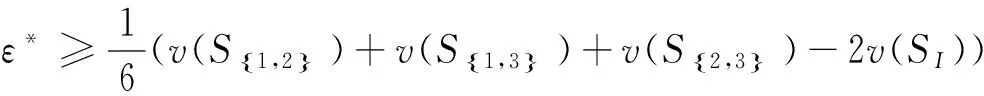
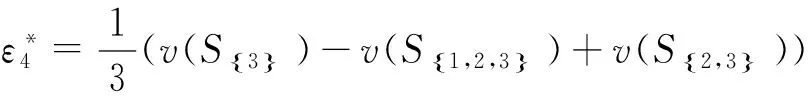
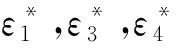
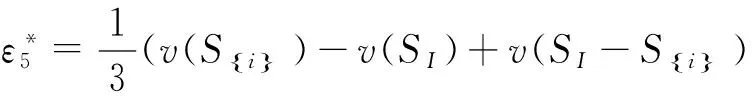
(17)

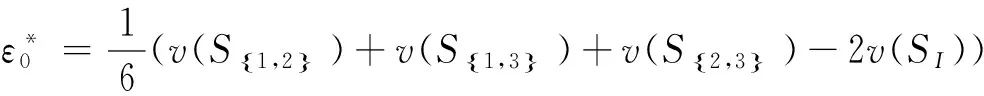
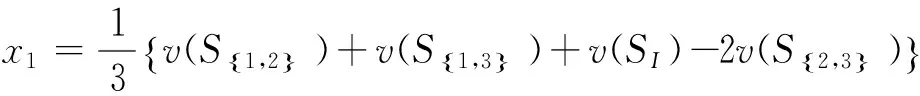
同理可得

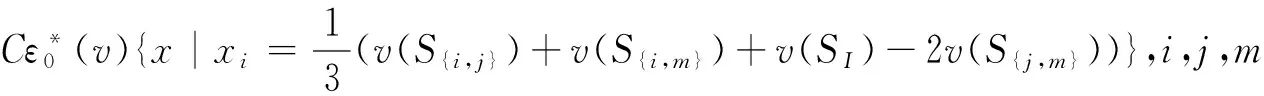
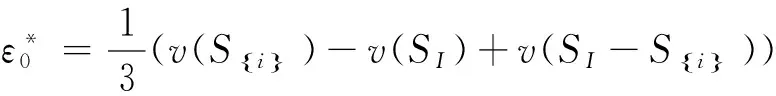
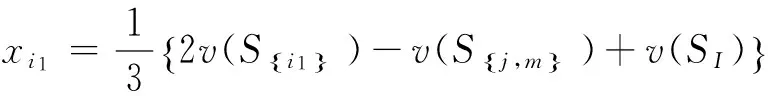
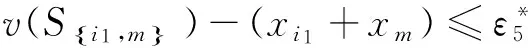
同理可求得

则最小核心为

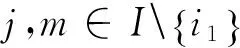
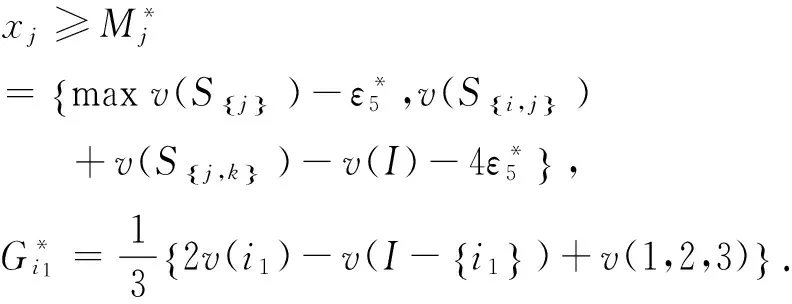
综合(Ⅰ)和(Ⅱ)可证.

在n人合作博弈中，最小核心总是有解的，最小核心求解出来的分配方案，满足群体合理性条件，但不一定满足个体合理性条件.

4 算例分析

表1 清晰联盟合作博弈的特征函数

表2 模糊联盟合作博弈的特征函数

利用定理2.1可求出最小核心为

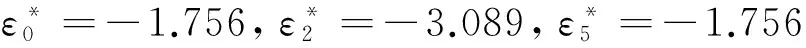
三家公司合作时，公司1所得的利益分配为1.756万元，公司2获得利益分配在[5.576,13.576]之间，公司3获得的利益分配在[4.756,12.576]之间.此方法可以应用到企业联盟利润分配问题中，不仅有固定的的计算公式，而且也弥补了核心常常为空集的情况.说明了文中所给出的三人模糊联盟合作博弈的最小核心解的合理性和实用性.

5 结 论

研究了三人模糊联盟合作博弈的最小核心的计算方法.把经典的合作博弈扩展到模糊联盟合作博弈上，并提出模糊联盟最小核心的定义，利用多维线性扩展模糊联盟合作博弈，得出三人模糊联盟合作博弈最小核心的计算公式.对于三个以上合作博弈的联盟最小核心算法，由于计算比较繁琐，有待进一步研究.此外可以进一步推广到特征函数为模糊集的合作博弈，以及联盟和特征函数均为模糊的合作博弈中.

[1] 李登峰. 模糊多目标多人决策与对策[M]. 北京: 国防工业出版社, 2003.

[2] R BRANZEI, D DIMITROV, S TIJS. Models in cooperative game theory: crisp, Fuzzy, and multichoice games[M]. Lecture Notes in Economics and Math-ematical systems. 2005.

[3] D BUMARIU, T KROUPA. Enlarged cores and bargaining schemesin games with fuzzy coalitions[J]. Fuzzy Sets and Systems, 2009, 160(5): 635-643.

[4] 李登峰. 直觉模糊集决策与对策分析方法[M]. 北京：国防工业出版社, 2012.

[5] D F LI. Decision and game theory in management with intuitionistic fuzzy sets[M]. Heidelberg:Springer-Verlag, 2012.

[6] R BRANZEI, D DIMITROV, S TIJS. Models in cooperative game theory[M]. Springer: Springer Publishing Press, 2008.

[7] Aubin J P. Coeur et valeur des jeux flous à paiements latéraux[J]. CR Acad. Sci. Paris, 1974(279):891-894.

[8] 孙红霞, 张强. 基于联盟结构的模糊合作博弈的收益分配方案[J]. 运筹与管理, 2010, 19(5): 84-89.

[9] 占家权, 张强. 一类模糊合作博弈资源与收益分配研究[J]. 运筹与管理, 2010, 19(2): 8-11.

[10]黄武军, 刘天虎, 许维胜等. 拟阵约束下TU模糊合作博弈的Banzhaf-Coleman值[J]. 运筹与管理, 2010, 19(6): 79-85.

[11]G OWEN. Multilinear extensions of games[J]. Management Sciences, 1972, 18(5): 64-79.

[12]F Y MENG, Q ZHANG. The shapley function for fuzzy cooperative games with multilinear extension form[J]. Applied Mathematics Letters, 2010, 23(5):644-650.

[13]孟凡永, 张强, 孙红霞. 模糊合作对策上的Banzhaf函数[J]. 系统工程学报, 2012, 27(1): 1-8.

[14]汪贤裕, 肖玉明. 博弈论及其应用[M]. 北京：科学出版社, 2008.

The Least Core for Three Person Ffuzzy Coalition Cooperative Game

BO Hong, NAN Jiang-xia

(School of Mathematics and Computing Science, Guangxi Colleges and Universities Key Laboratory of Data Analysis and Computation, Guilin University of Electronic Technology,Guilin, Guangxi 541004, China)

A fuzzy coalition cooperative game was studied, according to themultinear extension. The least core of three person fuzzy coalition cooperative game was defined and its' computational formulae was obtained. The research result shows that the least core of the three person fuzzy cooperative games with multilinear extension form is an extension of the least core of crisp cooperative games. The validity and applicability of the proposed method were illustrated with a real example.

operation research; the least core for fuzzy coalition cooperative game; multilinear extension

2016-05-25

国家自然科学基金(71561008，71461005)；广西自然科学基金(2012GXNSFAA053013，2014GXNSFAA118010)

卜 红(1990—)，女，河北邢台人，硕士研究生，研究方向为模糊决策与对策.E-mail:1614754797@qq.com

O225

A