超网络模型构建及特性分析*
刘胜久,李天瑞+,洪西进,3,王红军,珠 杰,4
1.西南交通大学 信息科学与技术学院,成都 611756
2.四川省云计算与智能技术高校重点实验室,成都 611756
3.台湾科技大学 资讯工程系,台北 10607
4.西藏大学 计算机系,拉萨 850000
超网络模型构建及特性分析*
刘胜久1,2,李天瑞1,2+,洪西进1,2,3,王红军1,2,珠 杰1,2,4
1.西南交通大学 信息科学与技术学院,成都 611756
2.四川省云计算与智能技术高校重点实验室,成都 611756
3.台湾科技大学 资讯工程系,台北 10607
4.西藏大学 计算机系,拉萨 850000
关联矩阵是超网络的一种表述形式,节点度、节点超度和超边度是度量超网络的一种方法。从关联矩阵出发对超网络进行研究,重点研究了自相似超网络及随机超网络,并给出了基于矩阵运算的超网络构建方法的若干性质。自相似超网络可通过对一个简单初始超图的关联矩阵进行迭代的Tracy-Singh积运算得到,而随机超网络可通过对多个简单初始超图的关联矩阵进行顺次的Tracy-Singh和运算得到。自相似超网络的分形维数不超过2,且当初始超图是连通的且非二分超图时,自相似超网络的直径不超过初始超图直径的两倍,即同时具有小世界特性。随机超网络的节点度、节点超度和超边度均呈正态分布。仿真实验证实了所构建的超网络的各项特性。
超网络;矩阵运算;自相似超网络;分形维数;随机超网络
1 引言
作为复杂系统的抽象表述,复杂网络一直受到人们极大的关注。20世纪中叶,Erdos和Renyi提出的ER随机网络模型[1]首开复杂网络的系统性研究,并奠定了后续近半个世纪对复杂网络研究的基础。随后,WS小世界网络模型[2]、NW小世界网络模型[3]和BA无标度网络模型[4]等一些重要的网络模型相继问世。
有别于ER网络模型泊松分布形态的度分布,WS网络模型与NW网络模型的度分布均呈指数分布,揭示了复杂网络的小世界特性;而BA网络模型的度分布呈幂律分布,揭示了复杂网络的无标度特性。小世界特性及无标度特性的提出开辟了复杂网络研究的新纪元,掀开了复杂网络研究的新局面,并被誉为复杂网络的两大特性。近年来,复杂网络的自相似特性受到人们极大的重视[5],被誉为复杂网络继小世界特性和无标度特性之后的第三大特性。当前复杂网络的研究主要包括经典的小世界网络、无标度网络及自相似网络等网络模型的研究与改进。Rudolph等人研究了有向WS小世界网络模型,提出了一种可精确描述WS小世界网络非对称性指数及聚集系数的新分析框架,包括表述其邻接矩阵的代数表达式[6]。Emmerich等人讨论了嵌入式无标度网络的结构和功能特性,同时将其与非嵌入式无标度网络的异同进行了对比分析[7]。张嗣瀛给出一个树状生长模型,并指出生长过程及自相似结构的涌现可集中由简单的幂律体现,幂律也是层层相似的自相似结构的成因。此外,这种模型的分形维数或相应的指数是系统功能的度量[8]。除此之外,矩阵等其他理论成果也逐步引入到复杂网络的研究中[9-10]。
在现实生活中,一般的网络或图并不能完全刻画真实世界网络的各项特性,普通图的每一条边只能连接两个节点的缺陷使其在描述真实网络时存在诸多不便。1970年,Berge提出了超图的概念[11-12],建立了无向超图理论,并应用拟阵来研究超图理论在运筹学中的应用。Feng等人提出了超图邻接矩阵的构建方法[13]。图的邻接矩阵是0-1矩阵,而超图的邻接矩阵却不一定是0-1矩阵。区别于普通图中两个节点之间的连接(边)只能表示一对节点之间的关系,超图中的超边可以包含任意多个节点,并用来表示多个节点之间的关系。Ernesto等人[14]认为凡是可用超图表示的网络就是超网络。
目前超网络的研究主要集中在基于现实世界的超网络各项特性的研究。Ernesto等人[15]研究了复杂超网络的子图中心度和聚集系数;Ghoshal等人[16]讨论了随机三部超图及它们的应用;Zlatic等人[17]定义和分析了基于三部超图模型的统计特性;Neubauer等人[18]利用超图理论给出了一种在标签网络中寻找最大连通子图的方法。在超网络模型构建方面,Zhang等人[19]建立了一种基于用户背景知识和对象,标签双重优先连接机制的超图增长模型;裴伟东等人[20]研究了基于一类三角形结构的动态网络演化模型,并利用平均场方法得到了这一类网络结构的理论解,证明了该类演化模型具有很多真实网络相似的无标度[4]和小世界现象[2-3];Wang等人[21]给出了一种基于超图的超网络动态演化模型,采用增长和优先连接机制逐步生成超网络,每次将新增加的若干个节点和超网络中已有的一个节点结合生成超边。胡枫等人[22]构建了一种超网络动态演化模型,并通过节点度、节点超度及超边度分析了该模型的基本拓扑性质,仿真实验发现,随着网络规模的增大,该动态演化模型的超度分布遵循无标度的特性。Yang等人[23]提出了一种局域世界超网络演化模型。此外,矩阵等其他工具已逐步应用到超网络模型的构建中[24],对超网络的研究也在持续深入[25]。
由于超网络在描述真实网络方面比通常的网络更具优势,在数据挖掘等领域也有着较为广阔的应用前景,引入新的研究方法与策略来刻画超网络是超网络研究的一大趋势。鉴于超网络的关联矩阵对应于超网络的拓扑结构,本文拟从关联矩阵的视角对超网络进行研究。主要是通过矩阵运算实现超网络的构建,即对一个简单初始超图的关联矩阵进行迭代Tracy-Singh积运算以构建自相似超网络,并对多个简单初始超图的关联矩阵进行Tracy-Singh和运算以构建随机超网络。同时给出了自相似超网络及随机超网络的若干性质,以期通过对超网络的研究洞悉真实复杂网络及复杂系统的特性。
2 预备知识
2.1 超图
设V=(v1,v2,…,vn)是一个有限集。若ei≠∅(i= 1,2,…,|E|),且,则称二元关系H=(V,E)为超图。其中V={v1,v2,…,vi,…}(1≤i≤|V|)是超图中所有节点的集合;E={e1,e2,…,ej,…}(1≤j≤|E|)是超图中所有超边的集合;|V|表示超图H中节点的数目,称为H的阶;|E|表示超图H中超边的数目。若两个节点属于同一条超边,则称这两个节点邻接;若两条超边的交集非空,则称这两条超边邻接。
定义1[11](关联矩阵,correlation matrix)超图H=(V,E)的关联矩阵C(H)是|V|×|E|的矩阵,若节点vi包含在超边ej中,则Cij=1,否则,Cij=0。
定义2[22](节点度,node degrees)超图H=(V,E)的节点度为该超边连接的节点数目,记为dHd(ei)。在超图的关联矩阵C(H)中,节点度即是对应的列中非零元素的数目,即:

定义3[22](节点超度,node hyperdegrees)超图H=(V,E)的节点超度为包含该节点的超边数目,记为dHhd(vi)。在超图的关联矩阵C(H)中,节点超度即是对应的行中非零元素的数目,即:

定义4(超边度,hyperedge degrees)超图H=(V,E)的超边度为超边所邻接的其他超边的数目,即与该超边至少存在1个公共节点的超边数,记为dHed(ei)。在超图的关联矩阵C(H)中,超边度即是与对应的列非正交的列数目,即:

胡枫等人在文献[22]中将超边度定义为除去该超边所对应的列外与此列非正交的列的数目。本文将超边度定义为超图的关联矩阵中所有的列与该超边所对应的列非正交的列的数目。由于非零列与自身一定非正交,本文中的超边度相当于在文献[22]的基础上增加了1。
基于节点度、节点超度和超边度的定义,可分别得到节点度分布、节点超度分布和超边度分布的定义。
定义5(节点度分布,node degrees distribution)超图H=(V,E)的节点度分布是指超图H中节点度的概率分布或频率分布。
定义6(节点超度分布,node hyperdegrees distribution)超图H=(V,E)的节点超度分布是指超图H中节点超度的概率分布或频率分布。
定义7(超边度分布,hyperedge degrees distribution)超图H=(V,E)的超边度分布是指超图H中超边度的概率分布或频率分布。
文献[10]提出用图的节点度分布多项式描述图的节点度分布。这里将图的度分布多项式应用到超图的节点度分布、节点超度分布和超边度分布中,分别得到超图的节点度分布多项式、节点超度分布多项式和超边度分布多项式。
定义8(节点度分布多项式,node degrees distribution polynomial)超图H=(V,E)的节点度分布多项式是指以超图H中节点度的频数为系数,以节点度为次数的单项式组成的多项式。
定义9(节点超度分布多项式,node hyperdegrees distribution polynomial)超图H=(V,E)的节点超度分布多项式是指以超图H中节点超度的频数为系数,以节点超度为次数的单项式组成的多项式。
定义10(超边度分布多项式,hyperedge degrees distribution polynomial)超图H=(V,E)的超边度分布多项式是指以超图H中超边度的频数为系数,以超边度为次数的单项式组成的多项式。
基于式(1)、式(2)和式(3),对超图H=(V,E)而言,其节点度分布多项式PolyHd(H)、节点超度分布多项式PolyHhd(H)和超边度分布多项式PolyHed(H)表述如下:
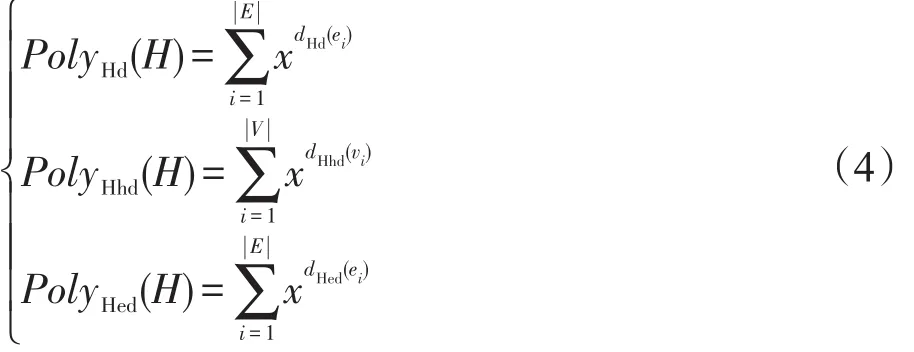
对式(4)中的节点度分布多项式PolyHd(H)进行分析,则可以得到如下结论:
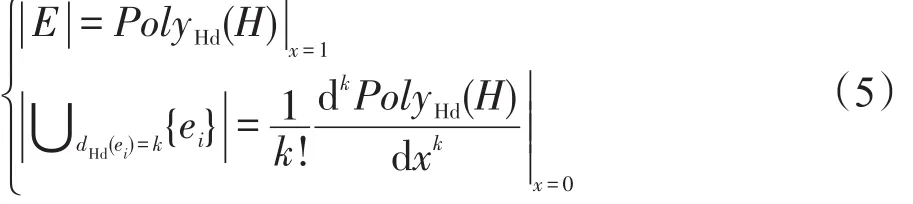
对式(4)中的节点超度分布多项式PolyHhd(H)进行分析,则可以得到如下结论:
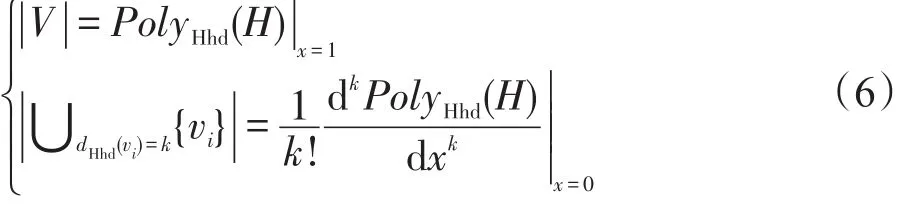
对式(4)中的超边度分布多项式PolyHed(H)进行分析,则可以得到如下结论:
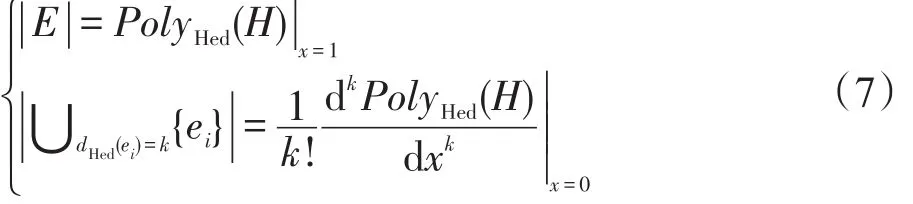
更进一步地分析,可以得到如下结论:
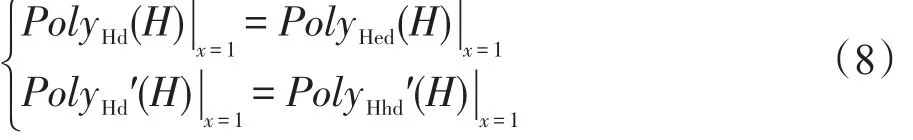
定义11[12](一致超图,uniform hypergraph)若超图H=(V,E)中所有的超边均包含相同数目的节点,则H称为一致超图,也称为均匀超图。若H所有的超边均包含n个节点,则称为n-均匀超图。
显然,2-均匀超图就是通常意义上的图。对2-均匀超图而言,其节点度就是通常意义上图的度。
定义12(超图密度,hypergraph gensity)超图H= (V,E)的密度是指超图H中所有超边包含的节点数目之和与最多可包含的节点数目总和的比值,表述为Gensity(H)。
由于一般情况下,超图H至少含有1条非空超边,故通常情况下,0〈Gensity(H)≤1。
2.2 分形理论
分形几何学是分形理论的数学基础,分形信息、分形设计和分形艺术等均由分形几何衍生而出[26]。分形理论最基本特点是用分数维度的视角和数学方法对客观事物进行分析研究,Cantor集、Koch雪花和Menger海绵等是常见的分形图形。
定义13[27]分形矩阵是通过对初始矩阵进行迭代相加运算而生成的一系列具有分形特性的矩阵。
最初将分形矩阵应用于图案生成中[28]。对一个给定的矩阵Am×n而言,分别用A的每一个元素aij(1≤i≤m,1≤j≤n)加上A的每一个元素所得到的矩阵去置换元素aij,得到一个局部与整体相似的新的矩阵,其整体结构具备与A相同的特性。令上述变换持续进行下去,可以得到一系列自相似的矩阵,…,其中是由的每一个元素与A相加后置换而成。上述迭代操作得到的一系列矩阵,…就是分形矩阵。文献[29]指出,迭代Kronecker积运算生成的矩阵也是分形矩阵。文献[10]提出分形矩阵形式的邻接矩阵对应的网络也是分形的,并指出对一个简单初始网络邻接矩阵进行迭代Kronecker积运算,可得到一个分形维数不超过2的自相似网络;对多个简单初始网络邻接矩阵进行顺次Kronecker和运算,可得到一个度分布呈正态分布的随机网络。这里将矩阵运算应用于超图的关联矩阵中。
2.3 矩阵理论
由于超图的关联矩阵中每一列代表一条超边,通常情况下可将超图的关联矩阵视为分块矩阵,其每一个分块矩阵均代表一条超边的列矩阵。类似于基于图的邻接矩阵的矩阵运算有Kronecker积运算及Kronecker和运算。对分块矩阵形式的超图的关联矩阵而言,基于Kronecker积运算还有另外两种积运算与对应的和运算,分别是Tracy-Singh积运算与Khatri-Rao积运算及Tracy-Singh和运算与Khatri-Rao和运算。Tracy-Singh积运算与Khatri-Rao积运算及Tracy-Singh和运算与Khatri-Rao和运算分别是Kronecker积运算及Kronecker和运算的变种。
矩阵A与B的Tracy-Singh积运算[30]表述为:
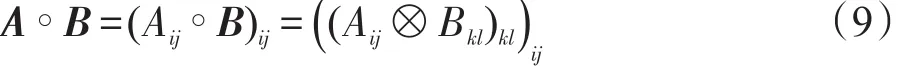
矩阵A与B的Tracy-Singh和运算[30]表述为:

矩阵A与B的Khatri-Rao积运算[31]表述为:

矩阵A与B的Khatri-Rao和运算[31]表述为:

Tracy-Singh积运算与Tracy-Singh和运算是将一个分块矩阵中的每一个分块与另一个分块矩阵中的每一分块进行运算,得到的新的分块矩阵的分块数目是两个分块矩阵分块数目的乘积。Khatri-Rao积运算与Khatri-Rao和运算只是将一个分块矩阵中的一个分块与另一分块矩阵中对应的分块进行运算,得到的新的分块矩阵的分块数目与参与运算的两个分块矩阵的分块数目相同。本文只考虑基于超图关联矩阵的Tracy-Singh积运算与Tracy-Singh和运算的超网络构建方法,至于基于超图关联矩阵的Khatri-Rao积运算与Khatri-Rao和运算的超网络构建方法将另文撰述。
3 基于矩阵运算的超网络模型构建
3.1 基于矩阵运算的自相似超网络模型构建
本文将分块矩阵的Tracy-Singh积运算应用于超图的关联矩阵中,得到一种基于矩阵运算的自相似超网络构建方法。
给定一个简单超图H=(V,E),其对应的关联矩阵为Cm×n,分别用C的每一列cj(1≤j≤n)乘以C的每一列所得到的矩阵去置换元素cj,得到一个局部与整体相似的自相似矩阵。令此变换过程不断进行下去,得到一系列自相似矩阵(对应于C的迭代Tracy-Singh积运算)。将这些自相似矩阵视为关联矩阵,其对应的超图就是H的迭代Tracy-Singh积超图。该超图具有自相似特性,即是自相似超网络。
Liu在文献[32]中论证了矩阵Tracy-Singh积运算与Khatri-Rao积运算的部分性质。在将超图的关联矩阵视为列矩阵组成的分块矩阵时,其Tracy-Singh积运算的结果等效于Kronecker积运算的结果。可以采用类似于文献[10]中图的邻接矩阵的Kronecker积运算的分析方法对超图关联矩阵的Tracy-Singh积运算进行分析。
对超图H=(V,E)及其对应的关联矩阵C而言,经过一次Tracy-Singh积运算后可以得到新的超图H(1)=(V(1),E(1))及其对应的关联矩阵C(1)。由于超图关联矩阵的行数代表超图的节点数目,而列数代表超图的超边数目,非零元素的数目与所有元素的数目之比代表超图的密度,于是有|V(1)|=|V|×|V|=|V|2,|E(1)|=|E|×|E|=(|E|)2,对超图密度而言,则有Gensity(H(1))=Gensity(H)×Gensity(H)。依此类推,可以得到:
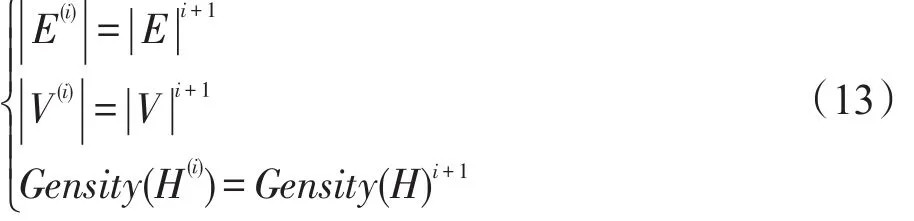
H(i)可简记为如下形式:

对式(13)进行分析,随着迭代次数i的增大,在i→∞时,得到的超网络节点数目、超边数目和密度为:
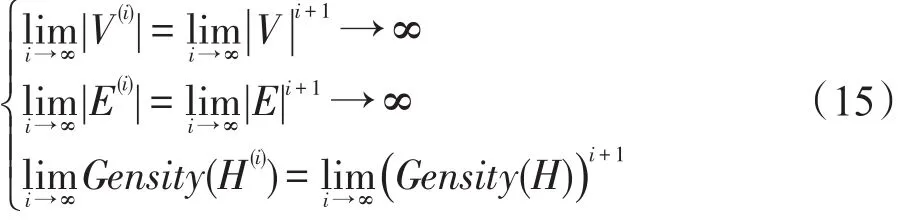
式(15)说明一个超图的迭代Tracy-Singh积超图在迭代次数趋近于无穷时,其节点数和超边数均趋近于无穷,而其密度取决于初始超图的密度。
超图的节点度分布多项式中单项式的次数代表超图的节点度,节点度分布多项式同时表述了初始超图的节点度分布及超图迭代Tracy-Singh积超图的节点度分布。可以通过对初始超图节点度分布多项式的运算得到超图迭代Tracy-Singh积超图的节点度分布多项式。对节点超度分布多项式及超边度分布多项式的分析类似,于是可以得到如下定理。
定理1一个超图的迭代Tracy-Singh积超图的节点度分布、节点超度分布和超边度分布可分别通过其节点度分布多项式、节点超度分布多项式和超边度分布多项式的系数相乘次数相乘的运算得到。
证明由于Tracy-Singh积运算是将一个分块矩阵的每一个分块与另一个分块矩阵的每一个分块分别进行Kronecker积运算,对于全部由列矩阵组成的分块矩阵而言,其Tracy-Singh积运算的结果等效于Kronecker积运算的结果。所得到的Tracy-Singh积运算的结果中每一列非零元素的数目就是超边对应的节点度,每一行中非零元素的数目就是节点对应的节点超度,与每一列非正交的列的数目就是超边对应的超边度。以节点度为例,若将矩阵每一列中非零元素的数目视为单项式的次数,在采用节点度分布多项式表述超图的节点度分布时,关联矩阵中列与列相乘反映到节点度分布多项式中就是次数与次数相乘,也即新得到的Tracy-Singh积超图的节点度分布多项式可视为初始超图节点度分布多项式系数相乘次数相乘的运算。对节点超度分布及超边度分布的分析与之类似。定理1得证。 □
根据定理1,若超度H的节点度分布、节点超度分布和超边度分布表述如式(4)所示,则对超图H(1)而言,其节点度分布、节点超度分布和超边度分布表述如下:
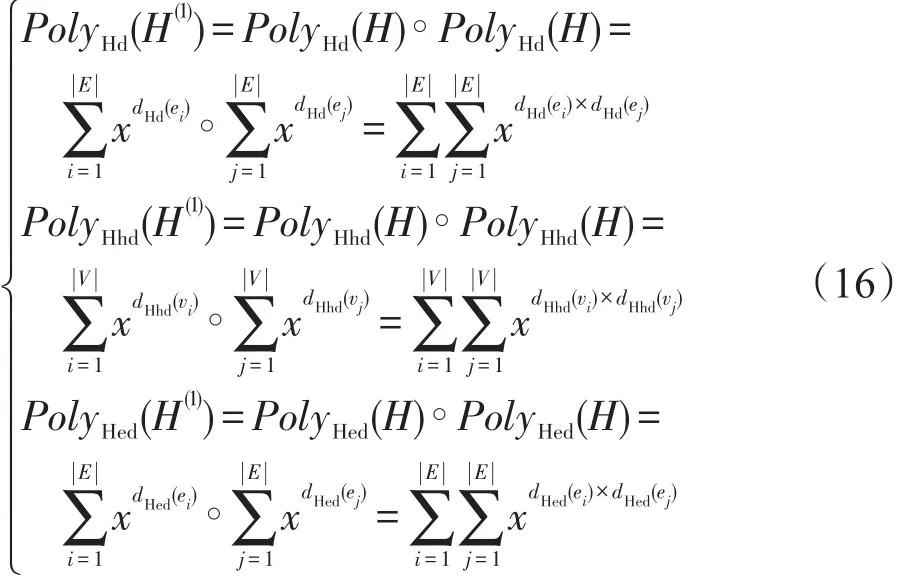
在通过Tracy-Singh积运算构建自相似超网络时,采用式(16),可以从理论上严格计算出新生成的自相似超网络的节点度分布多项式、节点超度分布多项式和超边度分布多项式,得到其节点度分布、节点超度分布和超边度分布。可将定理1进行推广并应用到不同超图的Tracy-Singh积运算中。
在分形理论中,分形维数是对分形图形进行度量的重要参数。由于关联矩阵与超网络的一一对应关系,对自相似超网络及其关联矩阵而言,它们的分形维数是相等的。可以对超网络关联矩阵的分形维数进行分析以间接得到超网络的分形维数。下文基于分形维数的定义,对此类自相似超网络的分形维数进行分析。
对于m×n的矩阵Am×n而言,基于A得到规模是其k倍的(mk)×(nk)矩阵需要k2个A进行简单的拼接。对于“拼接”这种操作(运算)而言,其分形维数表述如下:

于是,基于分形维数的计算方法,可以得出如下定理。
定理2一个超图的迭代Tracy-Singh积超图的分形维数为其超边包含的节点数之和的对数值和节点数与超边数乘积对数值的比值的两倍,即:
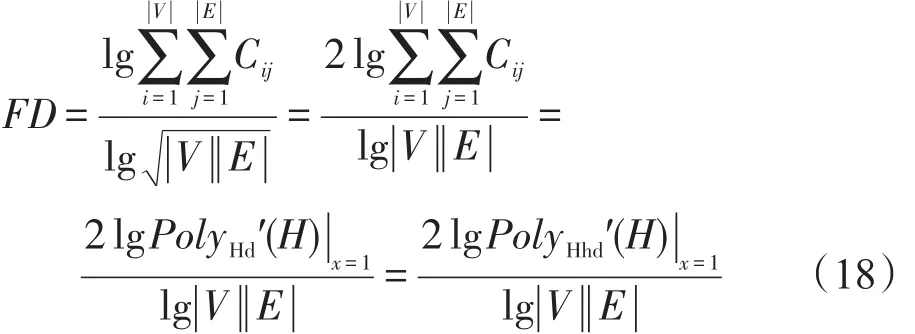
证明将Tracy-Singh积运算应用于超图H=(V,E)的关联矩阵C|V|×|E|时,以H(1)为例,其对应的关联矩阵为,从统计意义上可以认为其规模是C|V|×|E|的倍。但在运算过程中,只有在C(i,j)=1时才需要用C|V|×|E|替换C(i,j),共需要个C|V|×|E|进行选择性的“拼接”。定理2得证。 □
定理3一个超图的迭代Tracy-Singh积超图的分形维数不超过2。
证明对于超图H=(V,E)而言,即有,根据式(18),则有:
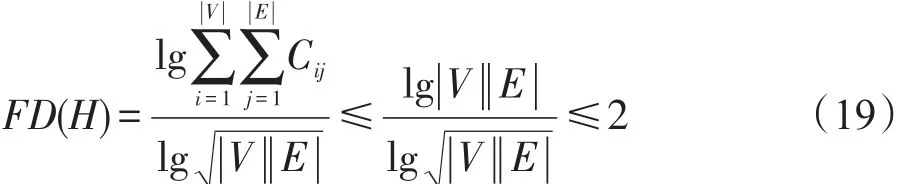
定理3得证。 □
一般情况下,对于超图H=(V,E)而言,ei≠∅(i= 1,2,…,|E|)。于是,基于定理3可以得出如下的引理。
引理1一个非空超图的迭代Tracy-Singh积超图的分形维数介于0到2之间。
证明对于非空超图H=(V,E)而言,有,根据式(18),则有:
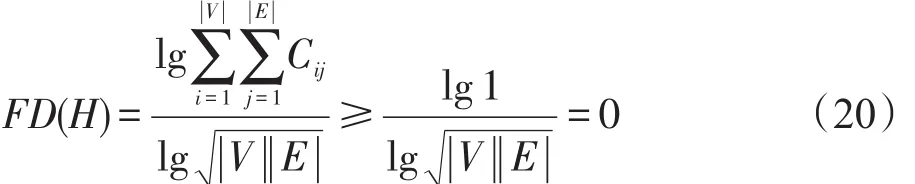
结合式(19),即有0〈FD(H)≤2。引理1得证。□
超图是图的超集,文献[10]基于图的邻接矩阵的迭代Kronecker积图形式的自相似网络的分形维数介于1到2之间,此处基于超图的关联矩阵的迭代Tracy-Singh积超图形式的自相似超网络的分形维数介于0到2之间。可以发现,自相似超网络的分形维数涵盖了自相似网络的分形维数,这从一个侧面诠释了超图是图的超集,图是超图的特例。
另外,一个分块矩阵的迭代Tracy-Singh积运算的结果也是分块矩阵,对基于超图关联矩阵的迭代Tracy-Singh积运算得到的分块矩阵进行分析,则可以得出如下定理。
定理4一个连通且非二分超图的迭代Tracy-Singh积超图的直径不超过初始超图直径的两倍。
证明设超图H=(V,E)的直径为d,则通过其任一节点均可在不超过d步内到达另一节点。在经过一次Tracy-Singh积运算得到的H(1)中,其对应的关联矩阵C(H(1))中分块矩阵内部的每一个节点也可在不超过d步内到达此分块矩阵内部的另一节点,而且一个分块矩阵也可在不超过d步内到达另一个分块矩阵,也即H(1)的直径不超过2d。由于应用Tracy-Singh积运算得到的超图H(i)(i≥1)对应的关联矩阵均是分块矩阵,则上述分析对任意的i(i≥1)均成立,即基于一个超图的关联矩阵的迭代Tracy-Singh积运算得到的Tracy-Singh积超图的直径均不超过2d。定理4得证。 □
注1定理4表明一个连通且非二分超图的迭代Tracy-Singh积超图的直径均相等,于是在具体的计算中只需要对H(1)的直径进行计算就可以得出所有此类自相似超网络的直径。
注2定理4只对连通且非二分超图成立,对非连通超图或二分超图不成立,因为二分超图的迭代Tracy-Singh积超图是非连通超图,而非连通超图的直径是无穷大。
更深入地分析,可以得到如下定理。
定理5一个n阶n-均匀超图的迭代Tracy-Singh积超图的直径恒为1,密度也恒为1。
证明n阶n-均匀超图的关联矩阵为全1矩阵,故其密度为1。从该超图的任一节点出发,可经1步到达其他任一节点,故其直径也为1。其迭代Tracy-Singh积超图的关联矩阵为全1矩阵,其密度也为1。从该全1矩阵对应的超网络的任一节点出发,均可经1步到达其他任一节点,故其直径也为1。定理5得证。 □
为更直观地刻画自相似超网络在不同维度下的度量情况,将一个连通且非二分超图的迭代Tracy-Singh积超图对应的自相似超网络与文献[10]中的自相似网络进行对比,对比结果如表1所示。
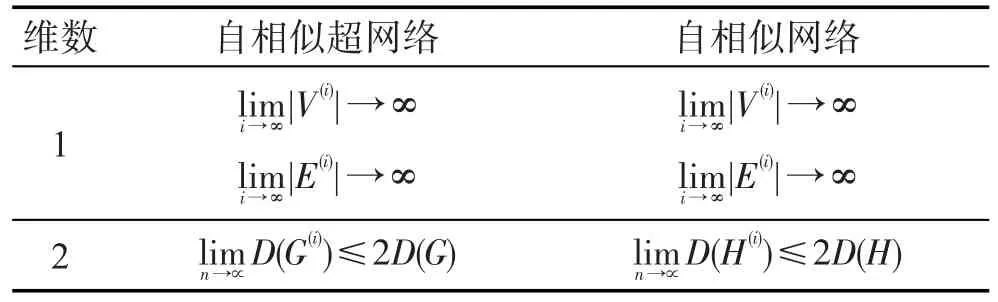
Table 1 Comparison between self-similarity hypernetwork and self-similarity network表1 自相似超网络与自相似网络对比表
从表1中可以看出,在维度为1时,自相似超网络的节点数和超边数与自相似网络的节点数和边数均趋近于无穷;在维度为2时,自相似超网络和自相似网络的直径均不超过初始超图或初始图直径的两倍。本文所构建的自相似超网络具有与自相似网络类似的特性。
从定理2可知,自相似超网络的分形维数只与初始超图的节点数、超边数和超边包含的节点数之和有关,可能存在多个拓扑结构不同的超图却拥有相同的节点数和超边数,且超边包含的节点数之和相等,也可能存在多个拓扑结构不同且节点数与超边数及超边包含的节点数之和也不同但分形维数却相同的超图,给出下述定义。
定义14(准自相似超网络,quasi self-similarity hypernetwork)准自相似超网络是指由多个节点数和超边数相等且超边包含的节点数之和也相等的初始超图对应的关联矩阵,通过Tracy-Singh积运算而得到的Tracy-Singh积超图。
定义15(泛自相似超网络,pan self-similarity hypernetwork)泛自相似超网络是指由多个超边包含的节点数之和的对数值及节点数与超边数乘积对数值的比值的两倍相等的初始超图所对应的关联矩阵,通过Tracy-Singh积运算而得到的Tracy-Singh积超图。
对准自相似超网络和泛自相似超网络进行分析,可以得到下述结论。
定理6准自相似超网络的分形维数等于对应的自相似超网络的分形维数。
证明根据定理2及式(10),自相似超网络的分形维数只与初始超图的节点数、超边数和超边包含的节点数之和有关。又根据定理1及式(16),准自相似超网络的节点数、超边数和超边包含的节点数之和与对应的自相似超网络的节点数、超边数和超边包含的节点数之和均相等。因此,准自相似超网络的分形维数与对应的自相似超网络的分形维数也相等。定理6得证。 □
引理2泛自相似超网络的分形维数等于对应的准自相似超网络的分形维数。
证明与定理6证明类似。 □
将超网络记为全集U,自相似超网络记为USS,准自相似超网络记为UQSS,泛自相似超网络记为UPSS,则可以得到如下定理。
定理7USS是UQSS的子集,UQSS是UPSS的子集,UPSS是U的子集,用公式表述为:

证明易证其成立。 □
3.2 基于矩阵运算的随机超网络模型构建
基于矩阵运算的随机超网络模型构建方法如下所示:对于一系列随机选择的初始超图H(1),H(2),…,,…来说,将Tracy-Singh和运算顺次应用于上述超图对应的关联矩阵可以得到一个新的矩阵,该矩阵对应的超网络是上述超图的Tracy-Singh和超图,即为随机超网络。
对于随机选择的初始超图H=(V,E)来说,可以认为其节点度分布、节点超度分布和超边度分布均是随机的,即均服从正态分布。而节点度、节点超度和超边度在其对应的节点度分布多项式、节点超度分布多项式和超边度分布多项式中即是对应的单项式次数,故反映在节点度分布多项式PolyHd(H)、节点超度分布多项式PolyHhd(H)和超边度分布多项式PolyHed(H)中,则是各个单项式的次数服从正态分布。
对两个超图Ha=(Va,Ea)、Hb=(Vb,Eb)及对应的节点度分布多项式PolyHd(Ha)与PolyHd(Hb)、节点超度分布多项式PolyHhd(Ha)与PolyHhd(Hb)、超边度分布多项式PolyHed(Ha)与PolyHed(Hb)来说,将Tracy-Singh积运算应用于Ha与Hb对应的关联矩阵所得到的Tracy-Singh积超图Hab的节点度分布、节点超度分布和超边度分布可分别通过PolyHd(Ha)与PolyHd(Hb)、PolyHhd(Ha)与PolyHhd(Hb)及PolyHed(Ha)与PolyHed(Hb)的 Tracy-Singh积运算得到,即有:
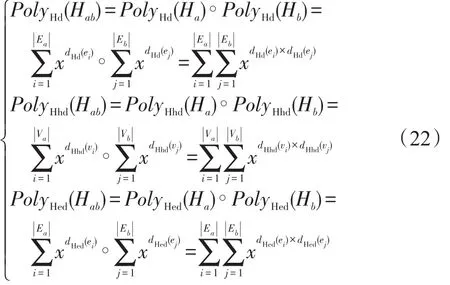
超图Hab的节点度分布、节点超度分布和超边度分布在其节点度分布多项式PolyHd(Hab)、超度分布多项式PolyHhd(Hab)和超边度分布多项式PolyHed(Hab)中也是其对应的单项式次数。从式(22)可以看出,两个相同或不同超图的Tracy-Singh积超图的节点度分布、节点超度分布和超边度分布均可以视为初始超图节点度分布、节点超度分布和超边度分布的非线性组合。对于将Tracy-Singh和运算应用于两个超图的关联矩阵所得到的新矩阵可以视为一个矩阵的每一列加上另一个矩阵的每一列,类似于Tracy-Singh积运算对超图的节点度分布多项式、节点超度分布多项式和超边度分布多项式的处理,将Tracy-Singh和运算应用于Ha与Hb对应的关联矩阵所得到的Tracy-Singh和超图Hab′的节点度分布、节点超度分布和超边度分布可以通过下式得到:
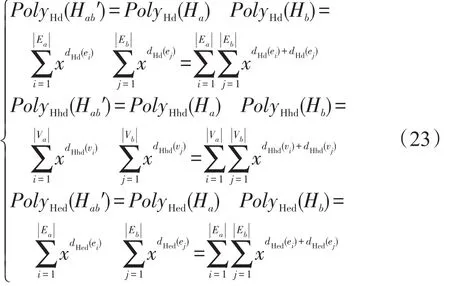
式(23)中节点度分布多项式、节点超度分布多项式和超边度分布多项式的运算即是通常的多项式乘法。可以看出,类似于对Tracy-Singh积运算采用系数相乘次数相乘的运算,对Tracy-Singh和运算采用系数相乘次数相加的运算也可以得到所生成的超网络的节点度分布、节点超度分布和超边度分布。可以将两个相同或不同超图的Tracy-Singh积超图的节点度分布、节点超度分布和超边度分布视为初始超图节点度分布、节点超度分布和超边度分布的非线性组合,并将两个相同或不同超图的Tracy-Singh和超图的节点度分布、节点超度分布和超边度分布视为初始超图节点度分布、节点超度分布和超边度分布的线性组合。对于随机选择的初始超图来说,其节点度分布、节点超度分布和超边度分布可以视为均服从正态分布。由于有限个正态分布的线性组合也是正态分布,基于多个初始超图的Tracy-Singh和超图的节点度分布、节点超度分布和超边度分布也服从正态分布。
在初始超图集合{H1,H2,…,Hi,…}中,对于顺次选择的H(1),H(2),…,H(i),…,H(n)并进行Tracy-Singh和运算得到的Tracy-Singh和超图H(n)来说,其节点数、超边数和密度可通过度分布多项式得到:
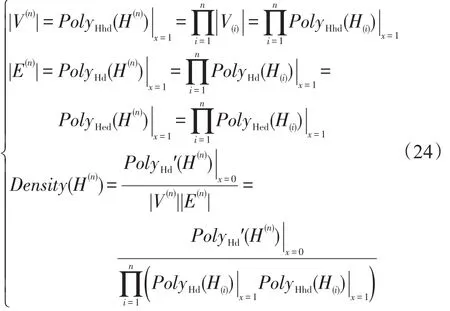
H(n)可简记为如下形式:

3.3 不同组合的超网络模型
前面分析了基于一个简单初始超图的迭代Tracy-Singh积运算可以得到自相似超网络,基于多个简单初始超图的Tracy-Singh和运算可以得到随机超网络。其实也可以基于一个初始超图进行迭代Tracy-Singh和运算或多个初始超图进行Tracy-Singh积运算。当然,也可以同时应用Tracy-Singh积运算及Tracy-Singh和运算。将上述超网络构建方法进行推广,可以得到一般情况下基于矩阵运算的超网络构建方法。基于一个、有限多个,乃至无穷多个初始超图的Tracy-Singh积运算和/或Tracy-Singh和运算共有9种组合,如表2所示。9种组合之间的关系如图1所示。
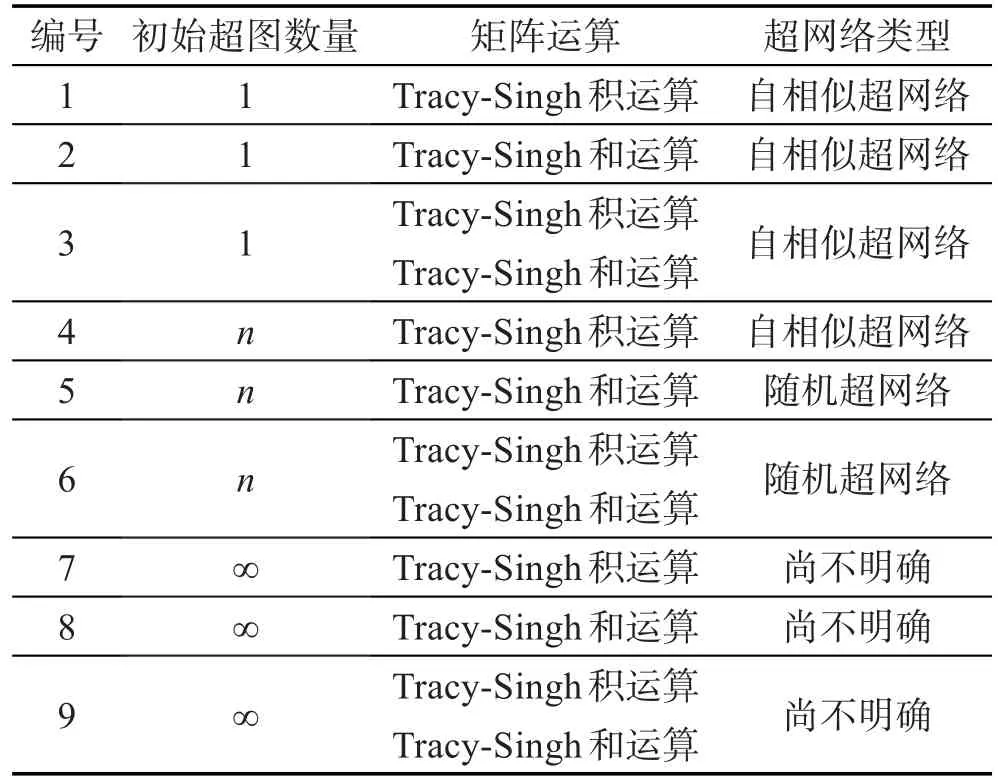
Table 2 Statistics of 9 combinations of hypernetwork based on matrix operation表2 基于矩阵运算的9种组合超网络统计表
4 基于矩阵运算的超网络理论分析
4.1 基于矩阵运算的超网络数量分析
在基于矩阵运算的超网络构建中,可以对初始超图节点度分布多项式、节点超度分布多项式和超边度分布多项式进行计算以得到Tracy-Singh积超图及Tracy-Singh和超图的节点度分布多项式、节点超度分布多项式及超边度分布多项式,随之得到其节点度分布、节点超度分布和超边度分布。由于超图的节点度分布多项式、节点超度分布多项式和超边度分布多项式无法反映超图的拓扑结构,一个相同的节点度分布多项式、节点超度分布多项式和超边度分布多项式组合可能对应多个拓扑结构不同的超图。
化学中描述化合物时需要分子式,但由于同分异构现象的存在,在描述化合物时,还需要结构式。一个相同的分子式可能对应多个不同的结构式,通过度分布多项式组合描述超网络与之类似。分子式对应于超网络的度分布多项式组合,而结构式对应于超网络的拓扑结构。与分子式对于结构式存在数量规律类似,节点度分布多项式、节点超度分布多项式和超边度分布多项式组合对于超网络的拓扑结构也存在数量规律。本文对基于矩阵运算的超网络数量进行研究,得到如下结论。
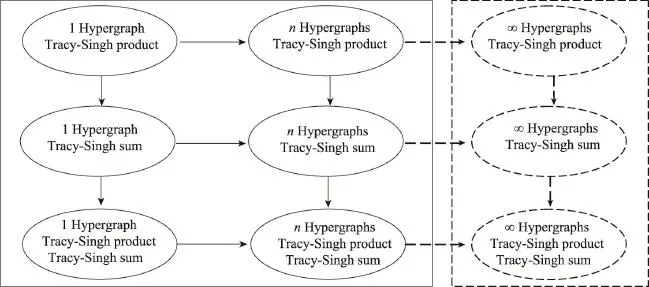
Fig.1 Relation of 9 combinations of hypernetwork图1 超网络9种组合关系图
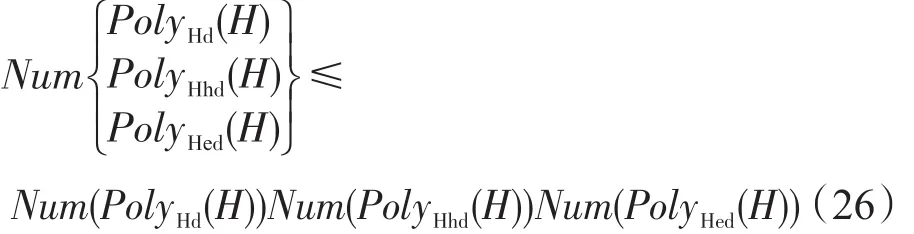
定理8超网络的数量不超过其节点度分布多项式、节点超度分布多项式和超边度分布多项式对应的复杂网络数量的乘积,即:证明对于超图H=(V,E)而言,其节点度分布、节点超度分布和超边度分布并不完全独立,三者之间存在一定的耦合关系,故超图的数量不超过其节点度分布多项式、节点超度分布多项式和超边度分布多项式对应的复杂网络数量的乘积。定理8得证。 □
注3定理8说明在难以直接计算一类节点度分布、节点超度分布和超边度分布组合已知的超网络数量时,可以通过计算其节点度分布多项式、节点超度分布多项式和超边度分布多项式对应的复杂网络的数量而间接得到该类超网络数量的上界,但仍未从根本上解决超网络的数量问题。对此类超网络的数量规律进行深入分析是后续研究的重要内容。
4.2 基于矩阵运算的超网络扰动与稳定分析
超网络扰动与稳定分析主要分析初始超图的波动对基于矩阵运算得到的超网络的影响,尤其是在增加或删除一个节点或一条超边及超边包含的节点变动时对超网络总体特性的影响。下面先分析其对自相似超网络的影响,包括分形维数、网络直径和度分布三方面的影响。
式(18)给出了基于初始超图H=(V,E)生成的自相似超网络分形维数,对增加或删除一个节点或一条超边及超边包含的节点变动对其分形维数的影响分析可以转化为对其分形维数的一阶导数进行分析。将式(5)及式(6)代入式(18),得到分形维数的一阶导数如下:
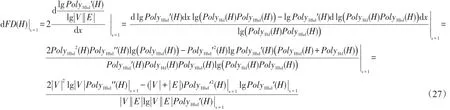
对于一个给定的超图H=(V,E)而言,其节点数|V|及超边数|E|是确定的。PolyHhd′(H)|x=1等于关联矩阵中非零元素的数目,是一个常数。分形维数的一阶导数dFD(H)|x=1取决于PolyHhd′(H)|x=1的取值,故分形维数与节点超度分布多项式的二阶导数密切相关。于是,在增加或删除一个节点或一条超边及超边包含的节点变动时,可以通过对节点超度分布多项式的计算近似得到分形维数的变化情况。
对自相似超网络直径的影响而言,由于直径尚无类似于分形维数的显式函数可以表述,故无法通过类似于分形维数的分析方法进行论述。但由于自相似超网络的直径不超过初始超图直径的两倍,而且初始超图中超边包含的节点变动对初始超图的直径没有显著的影响,可通过添加或删除一个节点或一条超边时对初始超图直径的影响来进行间接的分析。由于添加与删除是相对的,这里只分析添加即可,于是可得到如下结论。
定理9向初始超图添加一个节点后,自相似超网络直径的增加量不超过2。
证明向初始超图添加一个节点后,初始超图中节点之间的最短距离不受影响,但初始超图中任一节点与新增节点的距离不超过初始超图的直径加1,故自相似超网络直径的增加量不超过2。定理9得证。 □
定理10向初始超图添加一条超边后,自相似超网络直径的减少量不超过一半。
证明向初始超图添加一条超边后,初始超图中邻接的节点距离不发生变化,初始超图中不邻接的节点在添加超边后会导致初始超图中至少增加一个回路,回路中任意两个节点间的距离不超过节点数目的一半,故初始超图直径的减少量不超过一半,自相似超网络直径的减少量也不超过一半。定理10得证。 □
由于添加或删除一个节点或一条超边时对初始超图直径的影响存在确定的上限,故对最终生成的自相似超网络直径的影响也存在确定的上限。
对自相似超网络节点度分布、节点超度分布和超边度分布的影响而言,在具体的计算中是将节点度分布多项式、节点超度分布多项式和超边度分布多项式进行类似多项式乘法的系数相乘次数相乘的运算,将式(22)代入式(5)、式(6)和式(7)得到:
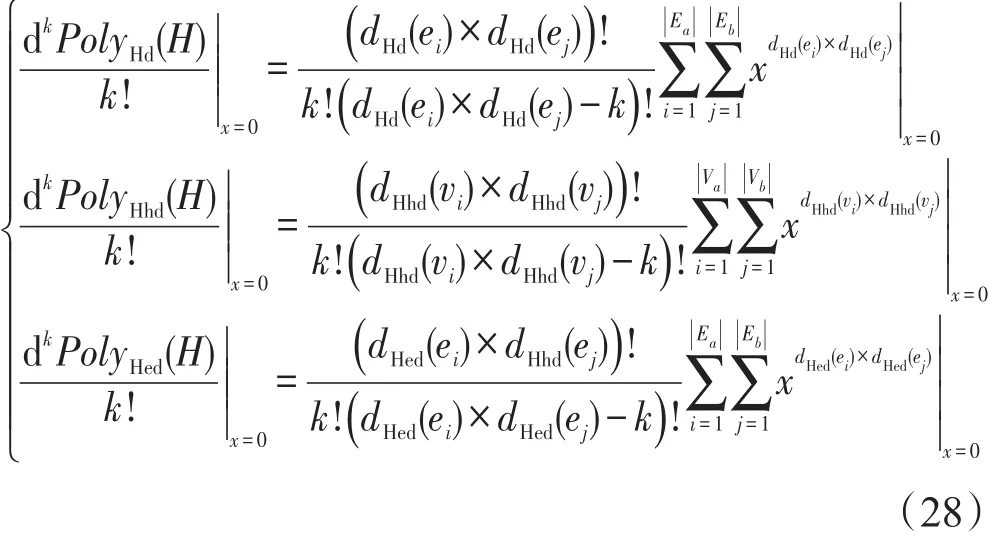
从式(28)可以看出,在添加或删除一个节点或一条超边时无法使用微分公式进行增量式的更新,即其不可微。故初始状况下添加或删除一个节点或一条超边时的细微差异会在以后随着迭代次数的增长而由于连锁反应会无限放大。
下面对随机超网络的影响进行分析,主要是对随机超网络节点度分布、节点超度分布和超边度分布的影响。对随机超网络而言,在具体的计算中是将节点度分布多项式、节点超度分布多项式和超边度分布多项式进行通常多项式乘法的系数相乘次数相加的运算。将式(23)代入式(5)、式(6)和式(7)得到:
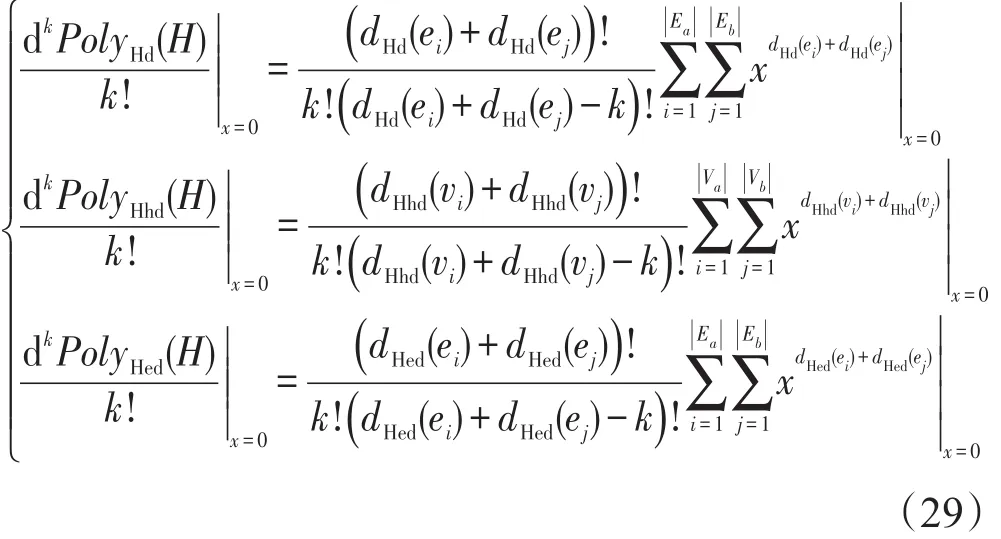
从式(29)可以看出,在添加或删除一个节点或一条超边时可以使用微分公式进行增量式的更新,即其可微。故初始状况虽然选用不同类型的超图,但最终生成的随机超网络节点度分布、节点超度分布和超边度分布的形态相同,均呈钟形的正态分布。
通过将微积分的工具与方法应用于超网络模型扰动与稳定的分析中,得到了一些定量的结论,但对超网络模型扰动与稳定的机理仍未透彻了解。后续工作的重点是继续深入利用微分方程和李雅普诺夫稳定性理论等对此进行深入的研究。
5 基于矩阵运算的超网络仿真实验
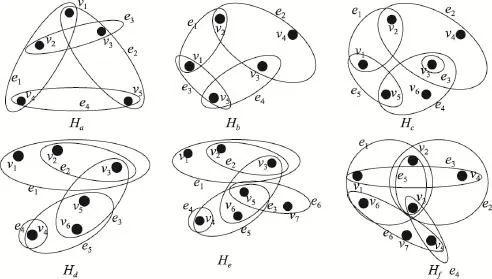
Fig.2 6 different initial hypernetworks图2 6个不同初始超图
本文选取6个简单的初始超图,如图2所示;其对应的信息及其生成的自相似超网络分形维数及网络直径如表3所示;其迭代20次后得到的自相似超网络节点度分布、节点超度分布和超边度分布分别如图3、图4和图5所示。
从图3、图4和图5中可以看出,基于一个简单初始超图的迭代Tracy-Singh积超图的节点度分布、节点超度分布和超边度分布不同于经典的ER随机网络的泊松分布、WS小世界网络的指数分布和BA无标度网络的幂律分布,这体现了其自相似超网络的特性。在图2中,Ha、Hb、Hc、Hd、He、Hf这6个初始超图之间只存在一个节点或一条超边的微小差异,但在图3、图4、图5中迭代20次后得到的自相似超网络的节点度分布、节点超度分布和超边度分布却差异巨大,其中Hb与Hc之间只存在一个节点及一条超边的差异,Ha与Hb只存在一条超边的差异,最终得到的结果却极为巨大。呈现出典型的“蝴蝶效应”特点。这其实就是超网络的“变数”。
同时,通过分析表3可以发现,在增加或删除一个节点或一条超边时,对最终得到的自相似超网络的分形维数影响不大,而且添加或删除节点对添加或删除超边对分形维数的影响更大,这可以通过表3中分形维数差别不大体现出来。而且,其对超网络直径的影响也是有限的,这可以通过表3中超网络直径的差别不超过2体现出来。这其实就是超网络的“定数”。定数与变数共存是超网络的特点,也是所有复杂网络与复杂系统的特点。

Table 3 Statistics of 6 different initial hypergraphs表3 6个不同初始超图统计表

Fig.3 Node degrees distributions of self-similarity hypernetworks based on 20 times iteration of 6 initial hypergraphs图3 6个初始超图迭代20次后得到的自相似超网络节点度分布
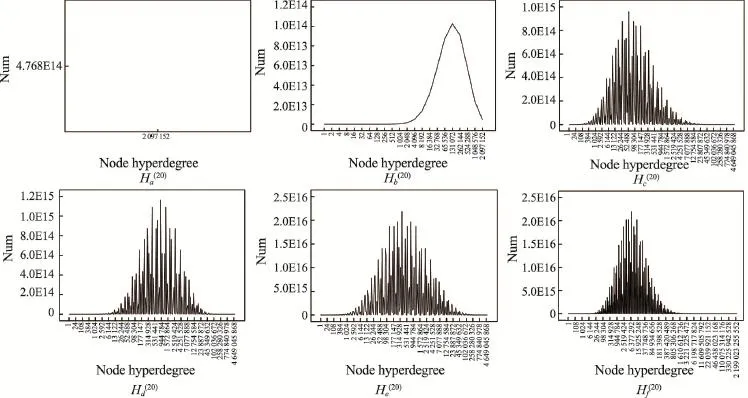
Fig.4 Node hyperdegrees distributions of self-similarity hypernetworks based on 20 times iteration of 6 initial hypergraphs图4 6个初始超图迭代20次后得到的自相似超网络节点超度分布
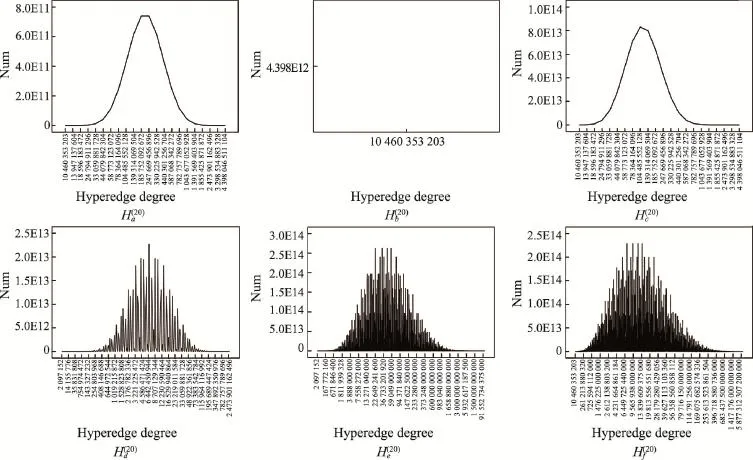
Fig.5 Hyperedge degrees distributions of self-similarity hypernetworks based on 20 times iteration of 6 initial hypergraphs图5 6个初始超图迭代20次后得到的自相似超网络超边度分布
同样基于图2中的6个初始超图,从中依次选取20个,允许重复选取,共选取6次,分别记为,选择次序如表4所示,得到的随机超网络的节点度分布、节点超度分布和超边度分布分别如图6、图7和图8所示。
从图6、图7、图8中可以看出,对随机选择的20个初始超图对应的关联矩阵进行Tracy-Singh和运算得到的超网络的节点度分布、节点超度分布和超边度分布均呈钟形的正态分布,这验证了有限个正态分布的线性组合仍是正态分布,也验证了对多个简单初始超图对应的关联矩阵进行Tracy-Singh和运算可以得到随机超网络。
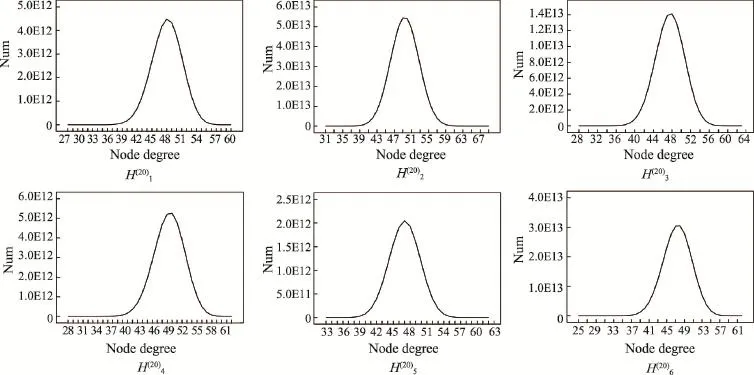
Fig.6 Node degrees distributions of random hypernetworks based on 20 initial hypergraphs selected randomly图6 随机选择20个初始超图后得到的随机超网络节点度分布

Table 4 6 random hypernetworks and corresponding 20 initial hypergraphs表4 6个随机超网络对应的20个初始超图选择表
6 结束语
对超网络的关联矩阵进行运算以构建超网络是一种新兴方法。本文将Tracy-Singh积运算及Tracy-Singh和运算应用于超网络的关联矩阵中,重点研究了两类超网络——自相似超网络与随机超网络的构建方法,并借助于节点度、节点超度和超边度对所构建的超网络进行分析。自相似超网络的自相似特性源于分形矩阵形式的关联矩阵,可以通过对一个简单初始超图的关联矩阵进行迭代的Tracy-Singh积运算得到;随机超网络的随机特性源于有限个正态分布的线性组合,可以通过对多个简单初始超图的关联矩阵进行顺次的Tracy-Singh和运算得到。对自相似超网络而言,其分形维数不超过2,且当初始超图为连通且非二分超图时同时具有小世界特性;对随机超网络而言,其节点度分布、节点超度分布和超边度分布均呈钟形的正态分布。基于矩阵运算所构建的超网络的节点度分布、节点超度分布和超边度分布可通过对节点度分布多项式、节点超度分布多项式和超边度分布多项式的运算得到。本文对超网络的数量及扰动与稳定等其他特性进行了一定程度的定量分析。后续研究的重点在于结合实际超网络的特点对基于矩阵运算所构建超网络的各项特性进行深入的分析研究,并探讨其在数据挖掘及真实网络与真实系统中的应用。
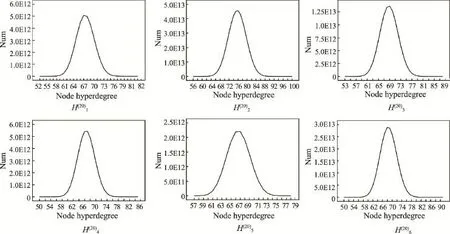
Fig.7 Node hyperdegrees distributions of random hypernetworks based on 20 initial hypergraphs selected randomly图7 随机选择20个初始超图后得到的随机超网络节点超度分布
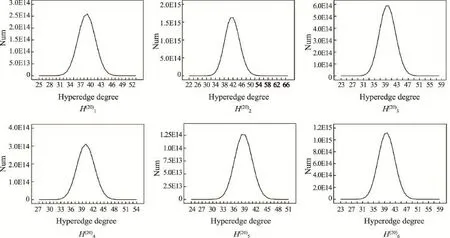
Fig.8 Hyperedge degrees distributions of random hypernetworks based on 20 Initial hypergraphs selected randomly图8 随机选择20个初始超图后得到的随机超网络超边度分布
[1]Erdos P,Renyi A.On random graphs I[J].Publicationes Mathematicae,1959,6:290-297.
[2]Watts D J,Strogatz S H.Collective dynamics of small-world networks[J].Nature,1998,393:440-442.
[3]Newman M E J,Watts D J.Renormalization group analysis of the small-world network model[J].Physics Letter A,1999, 263(4/6):341-346.
[4]Barabasi A L,Albert R.Emergence of scaling in random networks[J].Science,1999,286(5439):509-512.
[5]Song C,Jalvin S,Makse H A.Self-similarity of complex networks[J].Nature,2005,433:392-395.
[6]Rudolph L M,Muller L E.Algebraic approach to small-world network models[J].Physical Review E,2014,89(1):012812.
[7]Emmerich T,Bunde A,Havlin S.Structural and functional properties of spatially embedded scale-free networks[J].Physical Review E,2014,89(6):062806.
[8]Zhang Siying.The law of emergence of self-similar structures in complex systems and complex networks[J].Complex Systems and Complex Science,2006,3(4):41-51.
[9]Jalan S,Bandyopadhyay J N.Random matrix analysis of complex networks[J].Physical Review E,2007,76(4):046107.
[10]Liu Shengjiu,Li Tianrui,Horng Shijinn,et al.Research on complex network construction based on matrix operation[J]. Scientia Sinica Informationis,2016,46(5):610-626.
[11]Berge C.Graphs and hypergraphs[M].2nd ed.New York: Elsevier,1973:389-413.
[12]Berge C.Hypergraphs:combinatorics of finite sets[M].3rd ed.Amsterdam:North-Holl,1989:1-39.
[13]Feng Keqin,Li W C W.Spectra of hypergraphs and applications[J].Journal of Number Theory,1996,60(1):1-22.
[14]Ernesto E,Rodríguez-Velázquez J A.Subgraph centrality in complex networks[J].Physical Review E,2005,71(2):056103.
[15]Ernesto E,Rodríguez-Velázquez J A.Subgraph centrality and clustering in complex hypernetworks[J].Physica A,2006, 364(1):581-594.
[16]Ghoshal G,Zlatic V,Caldarelli G,et al.Random hypergraphs and their applications[J].Physical Review E,2009, 79(6):066118.
[17]Zlatic V,Ghoshal G,Caldarelli G.Hypergraph topological quantities for tagged social networks[J].Physical Review E,2009,80(3):036118.
[18]Neubauer N,Obermayer K.Hyperincident connected components of tagging networks[C]//Proceedings of the 20th ACM Conference on Hypertext and Hypermedia,Torino,Italy,Jun 29-Jul 1,2009.New York:ACM,2009:229-238.
[19]Zhang Zike,Liu Chuang.A hypergraph model of social tagging networks[J].Journal of Statistical Mechanics-theory and Experiment,2010.doi:10.1088/1742-5468/2010/10/ P10005.
[20]Pei Weidong,Xia Wei,Wang Quanlai,et al.Study of a class of dynamic complex network evolving models with a triangular structure[J].Journal of University of Science and Technology of China,2010,40(11):1186-1190.
[21]Wang Jianwei,Rong Lili,Deng Qiuhong,et al.Evolving hypernetwork model[J].European Physical Journal B,2010,77 (4):493-498.
[22]Hu Feng,Zhao Haixing,Ma Xiujuan.An evolving hypernetwork model and its properties[J].Scientia Sinica Physica, Mechanica&Astronomica,2013,43(1):16-22.
[23]Yang Guangyong,Liu Jianguo.A local-world evolving hypernetwork model[J].Chinese Physics B,2014,23(1):018901.
[24]Liu Shengjiu,Li Tianrui.A new hypernetwork model based on matrix operation[C]//Proceedings of the 2015 International Conference on Intelligent Systems and Knowledge Engineering,Taipei,China,Nov 24-27,2015:176-182.
[25]Yang Guangyong,Hu Zhaolong,Liu Jianguo.Knowledge diffusion in the collaboration hypernetwork[J].Physica A, 2015,419:429-436.
[26]Zhu Hua,Ji Cuicui.Fractal theory and its applications[M]. Beijing:Science Press,2011:262-316.
[27]Andre M B.On a class of fractal matrices(I)excess-matrices and their self-similar properties[J].International Journal of Bifurcation and Chaos,1992,2(4):841-860.
[28]Andre M B.Artistic design with fractal matrices[J].The Visual Computer,1993,9(5):233-238.
[29]Jeffrey S,Jorge S.Two methods for generating fractal[J]. Computers&Graphics,1989,13(2):185-191.
[30]Tracy D S,Singh R P.A new matrix product and its applications in matrix differentiation[J].Statistica Neerlandica, 1972,26(4):143-157.
[31]Khatri C G,Rao C R.Solutions to some functional equations and their applications to characterization of probability distributions[J].Sankhya,1968,30(2):167-180.
[32]Liu Shuangzhe.Matrix result on the Khatri-Rao and Tracy-Singh products[J].Linear Algebra and Its Applications, 1999,289(1/3):267-277.
附中文参考文献:
[8]张嗣瀛.复杂系统、复杂网络自相似结构的涌现规律[J].复杂系统与复杂性科学,2006,3(4):41-51.
[10]刘胜久,李天瑞,洪西进,等.基于矩阵运算的复杂网络构建方法研究[J].中国科学:信息科学,2016,46(5):610-626.
[20]裴伟东,夏玮,王全来,等.一类三角形结构动态复杂网络演化模型分析[J].中国科学技术大学学报,2010,40(11): 1186-1190.
[22]胡枫,赵海兴,马秀娟.一种超网络演化模型构建及特性分析[J].中国科学:物理学力学天文学,2013,43(1):16-22.
[26]朱华,姬翠翠.分形理论及其应用[M].北京:科学出版社, 2011:262-316.

LIU Shengjiu was born in 1988.He received the Ph.D.degree in complex network from Southwest Jiaotong University in 2015.Now he is a postdoctoral fellow at School of Information Science and Technology,Southwest Jiaotong University.His research interests include complex network,natural language processing and cloud computing,etc.刘胜久(1988—),男,湖北随州人,2015年于西南交通大学获得博士学位,现为西南交通大学信息科学与技术学院博士后,主要研究领域为复杂网络,自然语言处理,云计算等。

LI Tianrui was born in 1969.He received the Ph.D.degree in data mining from Southwest Jiaotong University in 2002.Now he is a professor and Ph.D.supervisor at Southwest Jiaotong University,IRSS fellow,and the senior member of IEEE,CCF and CAI.His research interests include data mining and knowledge discovery,granular computing and rough sets,cloud computing and big data,etc.
李天瑞(1969—),男,福建莆田人,2002年于西南交通大学获得博士学位,现为西南交通大学信息科学与技术学院教授、博士生导师,国际粗糙集学会(IRSS)会士,CCF、IEEE和CAI高级会员,主要研究领域为数据挖掘与知识发现,粒计算与粗糙集,云计算,大数据等。

HORNG Shijinn was born in 1957.He received the Ph.D.degree in computer science from National Tsing Hua University in 1989.Now he is a professor and Ph.D.supervisor at Department of Computer Science and Information Engineering,National Taiwan University of Science and Technology.His research interests include VLSI design,multiprocessing systems and parallel computing,etc.
洪西进(1957—),男,台湾桃园人,1989年于台湾清华大学获得博士学位,现为台湾科技大学咨讯工程系教授、博士生导师,主要研究领域为VLSI设计,多处理器系统,并行计算等。

WANG Hongjun was born in 1977.He received the Ph.D.degree in computer science from Sichuan University in 2009.Now he is an associate professor and M.S.supervisor at Southwest Jiaotong University,and the member of IEEE,CCF and ACM.His research interests include machine learning,semi-supervised learning and semi-supervised ensemble learning,etc.
王红军(1977—),男,四川广安人,2009年于四川大学获得博士学位,现为西南交通大学信息科学与技术学院副研究员、硕士生导师,CCF、IEEE和ACM会员,主要研究领域为机器学习,半监督学习,半监督集成学习等。

ZHU Jie was born in 1973.He is a Ph.D.candidate at Southwest Jiaotong University,and associate professor at Tibetan University.His research interests include data mining and natural language learning,etc.
珠杰(1973—),男,西藏日喀则人,西南交通大学博士研究生,西藏大学副教授,主要研究领域为数据挖掘,自然语言处理等。
Hypernetwork Model and Its Properties*
LIU Shengjiu1,2,LI Tianrui1,2+,HORNG Shijinn1,2,3,WANG Hongjun1,2,ZHU Jie1,2,4
1.School of Information Science and Technology,Southwest Jiaotong University,Chengdu 611756,China
2.Key Lab of Cloud Computing and Intelligent Technique of Sichuan Province,Chengdu 611756,China
3.Department of Computer Science and Information Engineering,National Taiwan University of Science and Technology,Taipei 10607,China
4.Department of Computer Science,Tibetan University,Lhasa 850000,China
+Corresponding author:E-mail:trli@swjtu.edu.cn
Correlation matrix describes hypernetwork briefly and intuitively.Hypernetwork can be characterized by node degree,node hyperdegree and hyperedge degree.This paper studies hypernetwork especially self-similar hypernetwork and random hypernetwork from the perspective of correlation matrix,and shows several properties of approaches for constructing hypernetwork based on matrix operation.Self-similar hypernetwork can be obtained by Tracy-Singh product on the correlation matrix of a simple initial hypergraph iteratively,and random hypernetwork can be obtained by Tracy-Singh sum on the correlation matrixes of multiple simple initial hypergraphs sequentially.Thefractal dimension of self-similar hypernetworks is no larger than 2.When the initial hypergraph is a connected and nonbipartite hypergraph,the diameter of self-similar hypernetwork does not exceed twice of that of the initial hypergraph, namely,it also shares a small-world property.The distributions of node degrees,node hyperdegrees and hyperedge degrees of random hypernetworks are normal.The results of simulation experiments validate the properties of the constructed hypernetwork.
hypernetwork;matrix operations;self-similar hypernetwork;fractal dimension;random hypernetwork
10.3778/j.issn.1673-9418.1603049
A
:TP393
*The National Natural Science Foundation of China under Grant Nos.61175047,61262058,61152001(国家自然科学基金);the Fund of the State Key Laboratory of Management and Control for Complex Systems,the Institute of Automation,Chinese Academy of Science under Grant No.20110102(中国科学院自动化研究所复杂系统管理与控制重点实验室开放课题).
Received 2016-02,Accepted 2016-04.
CNKI网络优先出版:2016-04-01,http://www.cnki.net/kcms/detail/11.5602.TP.20160401.1614.010.html
LIU Shengjiu,LI Tianrui,HORNG Shijinn,et al.Hypernetwork model and its properties.Journal of Frontiers of Computer Science and Technology,2017,11(2):194-211.

