两类矩阵对角化问题的探讨
张立华,赵琳琳,马立新
(德州学院,山东 德州 253023)
两类矩阵对角化问题的探讨
张立华,赵琳琳,马立新
(德州学院,山东 德州 253023)
矩阵对角化是高等代数中的重要内容,涉及到特征值、矩阵相似等基本问题,更是求解许多问题的工具。因此,就高等代数中经常遇到的一类单个矩阵对角化问题,给出一个一般结论,针对两个矩阵同时对角化问题,给出几个问题的证明,并且否定了一般结论的存在性,是有意义的。
高等代数;矩阵;对角化
0 引言
高等代数是现代数学的基础,同数学分析、解析几何构成现代数学的三大基石,是数学专业学生必修的核心基础课。如果一个矩阵可以相似于一个对角阵,则称该矩阵可以相似对角化,简称对角化[1]。矩阵对角化是高等代数中的重要内容,涉及到特征值、矩阵相似、二次型等基本问题,是高等代数教学重点之一,也是解决许多问题的必需工具[1-3]。实对称矩阵一定可以对角化,一般的数字矩阵不一定能对角化,两个数字矩阵还有可能同时对角化。笔者多年讲授高等代数,在对单个矩阵对角化问题总结归纳的基础上,给出了一个一般结论;对于两个矩阵的同时对角化问题,给出了几个问题的证明,并对一般结论的存在性进行了探讨。
1 一个矩阵的对角化问题
关于一个矩阵的对角化问题,文献[4]中给出了矩阵对角化的条件和应用,下面首先给出一个一般结论,这是文献[4]中例3的推广,有很多应用。
命题1 已知数域P上的n阶方阵A满足(A+mE)(A+bE)=0,其中m,b为不相等的实数,E是n阶单位矩阵,证明:
(1)A的特征值只能是-m或者-b;
(2)秩(A+mE)+秩(A+bE)=n;
(3)A一定能相似对角化;
(4)若秩(A+mE)=r,则-m为A的n-r重特征值,-b为A的r重特征值;
(5)如果V1和V2分别是齐次线性方程组(A+mE)X=0和(A+bE)X=0的解空间,那么
Pn=V1⊕V2。
证 (1)设a为矩阵A的特征值,则(a+m)(a+b)为矩阵(A+mE)(A+bE)的特征值;又由于(A+mE)(A+bE)=0,而零矩阵的特征值只能为0,所以(a+m)(a+b)=0。所以a=-m或者a=-b,从而A的特征值只能是-m或者-b。
(2)由于(A+mE)(A+bE)=0,所以秩(A+mE)+秩(A+bE)≤n。又由于(A+mE)-(A+bE)=(m-b)E,而m-b≠0,从而,秩[(A+mE)-(A+bE)]=秩((m-b)E)=n≤秩(A+mE)+秩(A+bE),所以秩(A+mE)+秩(A+bE)=n。
(3)设秩(A+mE)=r,则根据(2),秩(A+bE)=n-r,所以齐次线性方程组(A+mE)X=0有n-r个线性无关的解,而齐次线性方程组(A+bE)X=0有r个线性无关的解;也即特征值-m有n-r个线性无关的特征向量,特征值-b有r个线性无关的特征向量;由于属于不同特征值的特征向量是线性无关的,从而A有n个线性无关的特征向量,所以A一定能相似对角化。
(4)根据(3)的证明知道,若秩(A+mE)=r,则齐次线性方程组(A+bE)X=0有n-r个线性无关的解;从而特征值-m的重数≥n-r。同理,特征值-b的重数≥r。而特征值-m的重数+特征值-b的重数=n,所以特征值-m的重数为n-r,特征值-b的重数为r。
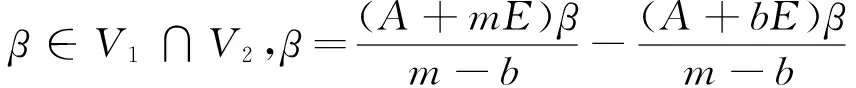
注:命题1的结论可以用来求特征值,判定矩阵是否对角化,也可确定特征子空间的维数和跟秩有关的其他问题。
例1 设n阶矩阵A是幂等矩阵,证明:Tr(A)=A的秩。

2 两个矩阵同时对角化的问题
这类题目比较难解,我们给出几个相关问题的证明。
例2 设A、B都是n阶实对称矩阵,AB=BA,证明:存在正交矩阵Q,使Q-1AQ与Q-1BQ同时为对角矩阵。

这里Ei表示单位矩阵。因为AB=BA,所以

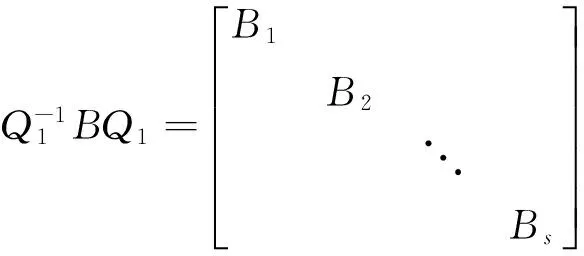

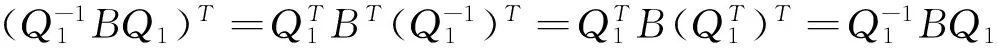

则

即Q是正交矩阵,且
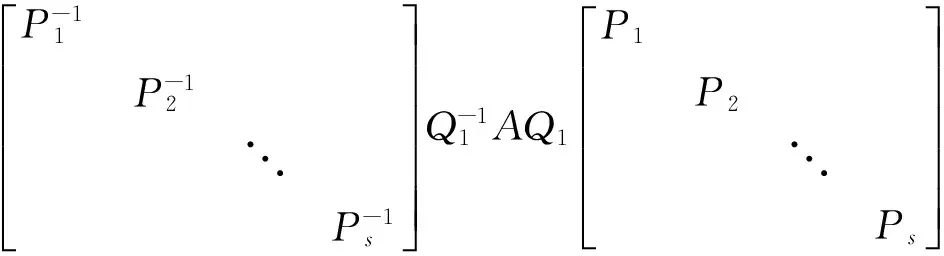


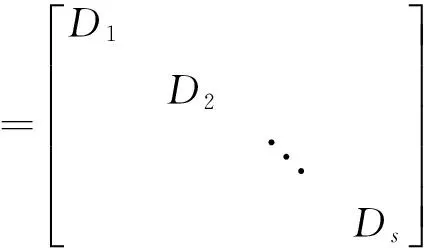
即Q-1AQ与Q-1BQ皆为对角矩阵。
例3 设A是n阶实对称矩阵,B是n阶方阵,满足B2=B,且AB=BA,证明:存在可逆矩阵Q,使Q-1AQ与Q-1BQ同时为对角形矩阵。

这里Ei表示单位矩阵。因为AB=BA,所以


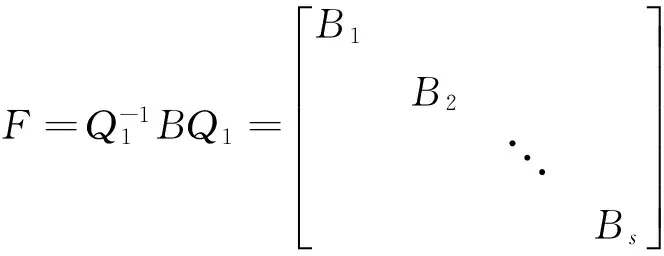


则由于Q1可逆,Pi(i=1,2,…,s)也可逆,所以Q是可逆矩阵,且
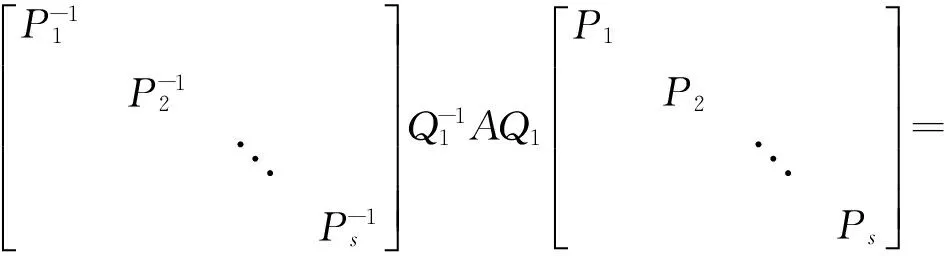

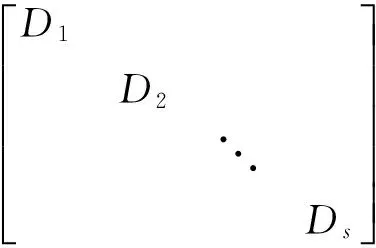
即Q-1AQ与Q-1BQ皆为对角矩阵。
例4 设A、B是两个n阶方阵,满足A2=4E,B2=B,且AB=BA,证明:存在可逆矩阵Q,使Q-1AQ与Q-1BQ同时为对角形矩阵。
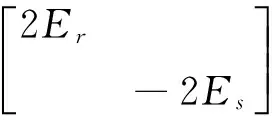
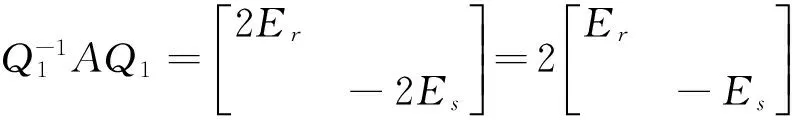
这里Er,Es表示单位矩阵。因为AB=BA,所以
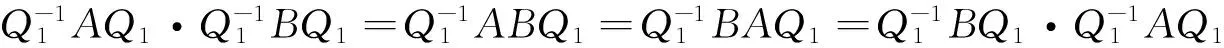


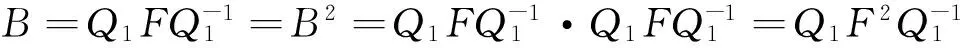
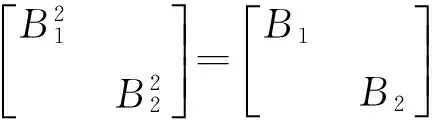
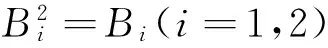
则由于Q1可逆,Pi(i=1,2)也可逆,所以Q是可逆矩阵,且
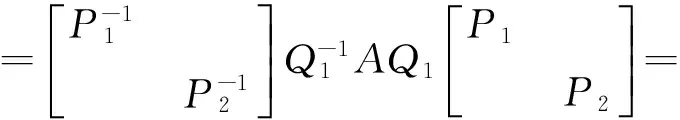
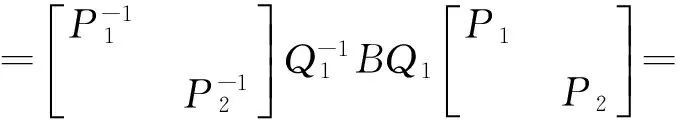
即Q-1AQ与Q-1BQ皆为对角矩阵。
例5 设A、B是两个n阶方阵,满足A2=E,B2=E,且AB=BA,证明:存在可逆矩阵Q,使Q-1AQ与Q-1BQ同时为对角形矩阵。
例5的证明跟例4基本一样,这里略去。例2至例5中的两个矩阵都是可交换的,不同的是:例2中是两个实对称矩阵,例3中一个实对称矩阵,一个可对角化的矩阵,例4和例5中是两个可对角化的矩阵。受例4、例5的启发,是不是两个可交换、都可以对角化的矩阵就能同时对角化呢?设A、B是两个n阶方阵,A、B均可对角化,且AB=BA,则可逆矩阵Q,使Q-1AQ与Q-1BQ同时为对角形矩阵。我们经过分析否定了这一点(实际上就是按照例2至例4的思路进行证明),或者说两个可交换、都可以对角化的矩阵,再加上一定的条件才可以同时对角化。
3 结语
本文探讨了一类单个矩阵的对角化问题,在原有工作的基础上给出了一个一般结论。对于比较复杂的两个矩阵同时对角化问题,我们给出了几个问题的证明,并且得出结论:两个可交换、都可以对角化的矩阵并不一定可以同时对角化。
[1] 王萼芳,石生明.高等代数[M].北京:高等教育出版社,2007.
[2] 杨子胥.高等代数[M].济南:山东科学技术出版社,2001.
[3] 周明旺.关于矩阵可对角化的一个充要条件[J].通化师范学院学报,2007,28(4):10-11.
[4] 张立华.高等代数教学中关于“矩阵对角化”的一点注记[J].廊坊师范学院学报(自然科学版),2013,13(4):8-11.
Study on Two Classes of Diagonalization of Matrix
ZHANGLi-hua,ZHAOLin-lin,MALi-xin
(DezhouUniversity,Dezhou253023,China)
Diagonalization of matrix, which has close connection with eigenvalue, similar matrix and so on, is important content in advanced algebra and is an essential tool to solve corresponding problems. A generalized conclusion on the diagonalization of a single matrix is given. Proofs on several problems of simultaneous diagonalization of two matrices are given, and the existence of generalized conclusion on these problems is negated, which proves to be of importance.
advanced algebra;matrix;diagonalization
2016-01-05
山东省自然科学基金资助项目(ZR2013AQ005)
张立华(1981-),女,理学博士,德州学院数学科学学院副教授,研究方向:孤立子与可积系统。
O151.21
A
1674-3229(2017)01-0005-04

