含多条裂纹梁的模态与振动疲劳寿命分析*

马一江， 陈国平

(南京航空航天大学机械结构力学及控制国家重点实验室 南京, 210016)



含多条裂纹梁的模态与振动疲劳寿命分析*

马一江， 陈国平

(南京航空航天大学机械结构力学及控制国家重点实验室 南京, 210016)

基于Paris公式，提出了一种含多条裂纹梁疲劳寿命预估的方法。在模态分析中，基于传递矩阵方法，利用无质量的弯曲弹簧等效裂纹，提出一种求解含有多条裂纹梁固有振型的方法,分析裂纹数目、裂纹位置、裂纹深度对裂纹梁固有频率的影响。在振动疲劳分析中，研究了在简谐激励作用下裂纹数目对裂纹尖端应力强度因子的影响。通过Paris疲劳裂纹扩展方程和同步分析法，考虑裂纹梁振动与裂纹扩展的相互作用，分析了裂纹数目和裂纹位置对裂纹梁疲劳寿命的影响。结果表明,裂纹数量、裂纹位置和深度对梁的模态参数和疲劳寿命有重要影响。

裂纹梁；传递矩阵法；固有频率；振动疲劳

引 言

工程结构一般处于振动环境中，振动产生的裂纹引起的疲劳破坏是大型工程结构失效的重要原因之一。含裂纹结构作为工程中大型结构的重要组成部分并大量使用，很多学者在这类结构的振动分析方面进行了大量的研究分析。由于加工和装配等原因，梁表面可能存在初始损伤。目前，针对含有单条裂纹梁结构的振动分析取得了一定的成果[1-3]；但是裂纹数目的增加导致裂纹梁结构的特征行列式的阶数增加，因此而针对含有多条裂纹梁结构的振动分析则面临很大的困难，很多学者针对含有多条裂纹梁的振动分析也进行了大量的研究[4-5]。Shifrin等[6]提出了一种新方法来求解含有多条横向裂纹梁的固有振型，这种方法大大缩减了裂纹梁特征行列式的阶数，使得多裂纹梁结构的振动分析大大简化。

随着断裂力学的发展，1960年前后，波音公司最先发现应力强度因子在疲劳裂纹扩展中起关键作用。1963年，Paris等[7]将疲劳裂纹扩展数据与应力强度因子幅值进行对比，发现疲劳裂纹扩展是由裂纹尖端应力强度因子幅值所控制的，由此开创疲劳断裂理论。张立军[8]利用变参数Weibull模型研究了宽带随机载荷作用下结构件的疲劳寿命，提高了疲劳寿命预测的精度。文献[9-11]也提出很多估算疲劳寿命的方法。利用这些方法，在已知裂纹尖端位置应力场的情况下，就能确定裂纹扩展到疲劳破坏时所要经历的振动循环次数。然而在这类疲劳破坏分析中，主要采用静力学方法来进行应力分析，忽略了疲劳裂纹扩展引起的结构固有振型的变化，使得结构疲劳寿命的预估与工程实际相差很大,因此结构动响应分析应该考虑疲劳裂纹扩展与振动的相互作用。刘文光等[12]基于Paris方程采用同步分析法研究了悬臂梁根部单条裂纹情况下悬臂梁的疲劳寿命,但是没有考虑裂纹相对位置和裂纹数目对疲劳寿命的影响。在工程实际中，结构损伤可能有很多处，也可能出现在悬臂梁表面的任意位置，所以振动和疲劳寿命分析时应该考虑裂纹数目和相对位置的影响。

笔者对含有多条横向裂纹悬臂梁进行了模态分析，用无质量的弯曲弹簧来代替结构裂纹，根据断裂力学的理论，推导了含多条裂纹梁的特征方程。通过数值模拟，分析了裂纹位置、裂纹深度和裂纹数量对梁固有频率的影响。在振动疲劳分析中，分析了裂纹数目对裂纹尖端应力场强度的影响。基于Paris疲劳裂纹扩展方程，考虑裂纹梁振动与裂纹扩展的相互影响，采用同步分析方法，分析了裂纹数目和裂纹相对位置对裂纹梁疲劳寿命的影响，为含多条裂纹梁结构的疲劳寿命预测提供了一种方法。

1 模型建立

如图1所示，理论分析对象为一个等截面矩形梁，长为L，宽为b，高为h，梁表面存在n条横向裂纹，每条裂纹离固定端的位置分别为L1，L2，…，Ln。

根据Dimarogonas和Paipeties[13]理论，该裂纹梁内每条裂纹的局部柔度可以表示成如下形式

(1)

其中：E为梁材料的弹性模量;I为梁横截面的惯性矩;ri=ai/h为第i条裂纹的相对裂纹深度;ai为第i条裂纹的深度;f(ri)为第i条裂纹的局部柔度函数，可以由应变能密度函数求得

(2)

2 模态分析

以各条横向裂纹为端点，整段梁被n条裂纹分成n+1段完整梁，每段梁的长度分别为l1，l2，…，ln+1，根据Bernoulli-Euler理论，每段梁的无阻尼弯曲振动微分方程为

(3)

方程(3)的解可以表示为

(4)

其中：

根据材料力学，可以推导出如下关系式

在任意一段梁的两端截面，应用以上关系式，可以得到

改写成矩阵形式，可得

DR=TiDL

(5)

其中：Ti称为该多裂纹梁第i段的传递矩阵；li为该多裂纹梁第i段长度。

方程(4)中的待定系数可以表示为

(6)

即可得到每段梁的振型函数。

在该多裂纹梁的每条裂纹位置，根据挠度、弯矩和剪力的连续性和转角的相容关系，裂纹的左右两边截面的挠度、转角、弯矩和剪力可以表示为

(7)

改写成矩阵形式

DR=SiDL

(8)

其中：Si为该多裂纹梁第i条裂纹位置的传递矩阵。

因此，对于整个多裂纹梁，右端状态矢量和左端状态矢量间的传递关系可以表示为

DN=HD1

(9)

其中：H为含n条裂纹梁的传递矩阵。

H=Tn+1SnTnSn-1…T2S1T1

(10)

一般情况下，在导入边界条件时，其中两个边界条件为零，因此可以推导出一个2×2的特征矩阵H1，使得本方法在求解多裂纹梁的固有频率时分析过程大大简化，则该裂纹梁的频率方程为

detH1=0

(11)

这样由方程(11)可求得该裂纹梁的任意阶固有频率，对应的固有振型可通过方程(4)获得。

3 振动疲劳分析

3.1 动力学响应分析

假设该裂纹梁为一个左端固定、右端自由的悬臂梁，在梁的自由端作用垂直方向的简谐激励F0eiωt。随着裂纹的扩展，结构的动态特性是时变的，因此取该裂纹梁结构的某一瞬态进行分析，则对应的边界条件为

(12)

将方程组(12)代入式(9)，可以得到第1段梁固定端位置的挠度W1(0)、转角θ1(0)、弯矩M1(0)和剪力Q1(0)；将得到的这些初始值再代入方程(6)，可以得到第1段梁振型函数对应的系数c11，c12，c13，c14，即可求得第1段梁的振型函数。依次类推，可以得到该裂纹梁上任意段梁的振型函数。

由于图(1)中，该梁上的横向裂纹属于工程中最常见且破坏程度最严重的裂纹形式——张开型(I型)裂纹，所以以I型裂纹为研究重点。根据HOOKE定律

(13)

对于第i段梁，长度为li，可以得到该段梁表面的动应力响应

(14)

其中：y为梁表面离梁中面的距离。

(15)

则该段裂纹梁右端，即裂纹尖端的应力强度因子表达式为

(16)

其中：ai为第i条裂纹的深度。

根据本研究的裂纹类型和加载形式[14]，形状函数为

(17)

3.2 基于断裂理论的振动疲劳分析

3.2.1 动应力强度因子

动应力强度因子是在振动环境下表征裂纹尖端应力场分布的物理量，裂纹尖端动应力强度因子的一般表达式为

(18)

其中：ΔKI为动应力强度因子的振幅；Δσd为动应力的振幅；a为裂纹长度；Y(ri)为形状函数(与裂纹大小、位置有关)。

若该梁受到简谐激励作用，并且裂纹为I型(张开型)裂纹，则裂纹尖端的动应力强度因子振幅可表示为

(19)

将式(15)代入式(19)，即可得到任意条裂纹尖端动应力强度因子振幅的表达式：

(20)

3.2.2 疲劳裂纹扩展速率

Paris公式，或称疲劳裂纹扩展方程，是疲劳寿命预测应用最广泛且最简单的公式。该公式建立了疲劳裂纹扩展速率与动应力强度因子振幅ΔK之间的关系，为疲劳断裂问题的研究开辟了最主要的途径。在线弹性断裂力学范围内中等应力状态下，Paris公式能较好地预测直裂式裂纹结构的疲劳寿命。Paris公式的表达式为

(21)

其中：C，n为材料常数；da/dN表示直裂式裂纹的疲劳扩展速率。

因此利用Paris方程来模拟该裂纹悬臂梁疲劳裂纹的扩展，将式(20)代入式(21)，即可得到任意条裂纹的疲劳扩展速率模型

(22)

3.2.3 疲劳裂纹扩展分析

研究表明：在简谐激励作用下，结构的受迫振动会导致疲劳裂纹的扩展；结构疲劳裂纹的扩展同样会改变结构原有的动态特性，从而导致裂纹尖端区域应力场分布发生变化，并最终影响裂纹的疲劳扩展速率。两者之间存在相互作用，并相互影响。因此，笔者采用同步分析方法，即裂纹悬臂梁的振动模态分析与疲劳裂纹扩展寿命的估算同步进行。假设在每一个振动周期内裂纹的相对深度是不变的，裂纹扩展发生在每一个振动周期结束时。

具体的步骤是，假设该裂纹梁每振动一周计算出的动应力幅值为一个恒定值，利用式(22)计算周期载荷作用下，裂纹梁每振动ΔNj周的任意条裂纹的疲劳扩展增量

(23)

其中：Δaij为第i条裂纹第j次循环的裂纹增量；ΔNj=Nj-Nj-1。

取ΔNj=1，则有

da/dN≈Δaj/ΔNj

(24)

所以，裂纹梁上第i条裂纹第j次循环的裂纹增量的表达式为

(25)

结构受到恒定振幅简谐激励作用时，裂纹的最终深度可通过叠加法计算，表达式为

(26)

其中：ai0为裂纹梁上第i条裂纹的初始深度；k为总振动循环次数；aik为第i条裂纹振动k次之后的裂纹总深度。

3.2.4 疲劳裂纹失效判据

为了判断该裂纹悬臂梁是否失效，现采用以下准则作为失效判据。

准则1：如果该裂纹悬臂梁上任意条裂纹扩展至梁的中面时，就认为该结构已经破坏

ai≥ac

(27)

其中：ac为临界裂纹长度，取ac=h/2。

准则2：如果该裂纹悬臂梁上任意一条裂纹尖端应力强度因子大于材料的断裂韧性，就认为该结构已经发生失稳断裂

(28)

其中：Kc为材料的断裂韧性；Kmax为最大应力强度因子。

4 数值算例与结果分析

4.1 多处裂纹对梁固有频率的影响

4.1.1 裂纹数目对梁固有频率的影响

固定该裂纹悬臂梁上一条裂纹的相对位置为L1/L=0.1，初始裂纹深度为a10=0.002 m。

若该裂纹梁上仅有一条裂纹时，即为该固定的裂纹。若该裂纹梁上有两条裂纹时，第1条裂纹为该固定裂纹；第2条裂纹的相对位置为L2/L=0.3，初始裂纹深度为a20=0.002 m。若该裂纹梁上有3条裂纹时，第1条裂纹为该固定裂纹；第2条裂纹的相对位置为L2/L=0.3，初始裂纹深度为a20=0.002 m；第3条裂纹的相对位置为L3/L=0.5，初始裂纹深度为a30=0.002 m。3种情况对应的第1阶固有频率列入表1中。

若将该固定裂纹的相对位置改为L1/L=0.15，其他情况不变。3种情况对应的第1阶固有频率列入表1中。

若将该固定裂纹的相对位置改为L1/L=0.2，其他情况不变。3种情况对应的第1阶固有频率列入表1中。

表1 裂纹条数不同时裂纹梁的固有频率

Tab. 1 Natural frequencies of the cracked beam with different number of cracks Hz

表1数据显示，固定裂纹悬臂梁上某一裂纹的相对位置和深度，随着裂纹条数的增加，裂纹梁固有频率逐步减小。在裂纹数目、相对位置和深度都相同时，随着第1条裂纹远离悬臂梁固定端，该裂纹梁第1阶固有频率逐步增大。

4.1.2 裂纹相对位置和深度对裂纹梁固有频率的影响

1) 假设该裂纹悬臂梁,仅有两条横向裂纹，第1条裂纹的深度为a10=0.002 m，第2条裂纹的深度为a20=0.002 m，两条裂纹在不同位置时对应的固有频率如图2所示。

图2 裂纹深度一定时，裂纹梁第1阶固有频率随着裂纹相对位置的变化规律Fig.2 Variation of the first order natural frequencies of the cracked beam along with the position of the cracks

由图2可以得到，随着两条裂纹中任意一条裂纹逐渐远离固定端，该裂纹梁的固有频率均逐渐增大；当两条裂纹非常接近时，该裂纹梁的固有频率相对较大。

2) 假设该裂纹悬臂梁仅有两条横向裂纹，第1条裂纹的相对位置为L1/L=0.1，第2条裂纹的相对位置为L2/L=0.5，两条裂纹在不同深度时，该裂纹悬臂梁第1阶固有频率的变化规律如图3所示。

由图3可以得到，随着该裂纹梁上两条横向裂纹中任意一条裂纹相对深度的逐步增大，该裂纹梁的第1阶固有频率逐步减小；第1条裂纹(靠近悬臂梁固定端的裂纹)的深度变化对该裂纹梁固有频率的变化影响比较大，随着第1条裂纹深度的增加，该梁第1阶固有频率减小的幅度较大。

4.2 多处裂纹对裂纹尖端应力强度因子的影响

假设在该裂纹悬臂梁的自由端作用一个垂直方向的简谐激励，激励幅值为50 N，激励频率为裂纹梁的固有频率。裂纹的条数、相对位置和深度与章节4.1.1完全相同，则得到第1条裂纹尖端应力强度因子的值列入表2中。

图3 裂纹相对位置固定时，裂纹梁第一阶固有频率随着裂纹深度的变化规律Fig.3 Variation of the first order natural frequencies of the cracked beam along with the depth of the cracks

表2 裂纹条数不同时，裂纹梁第1条裂纹尖端应力强度因子

Tab. 2 Stress intensity factors at the first crack tip of the cracked beam with different number of cracks

裂纹数目L1/L=0．1L1/L=0．15L1/L=0．217．6209×1076．9851×1076．3558×10727．6747×1077．0359×1076．4032×10737．6965×1077．0564×1076．4224×107

表2数据显示，固定裂纹悬臂梁上第1条裂纹(靠近固定端的裂纹)的相对位置和深度随着裂纹条数的增加，该裂纹梁第1条裂纹尖端应力强度因子的值逐步增大。在裂纹数目、相对位置和深度相同时，随着第1条裂纹逐渐远离该悬臂梁固定端，该裂纹梁第1条裂纹尖端应力强度因子也逐步减小。

4.3 多处裂纹对梁疲劳寿命的影响

假设在该裂纹悬臂梁的自由端作用一个垂直方向的简谐激励，激励幅值为50 N，保持不变。

4.3.1 共振状态下阻尼对梁疲劳寿命的影响

假设该裂纹悬臂梁仅有一条裂纹，且该裂纹的相对位置为L1/L=0，初始裂纹深度为a10=0.002 m。则当该裂纹悬臂梁处于共振状态下，阻尼损耗因子分别为γ=0.005，γ=0.01，γ=0.05，γ=0.1时，该裂纹悬臂梁的疲劳寿命如图4所示。

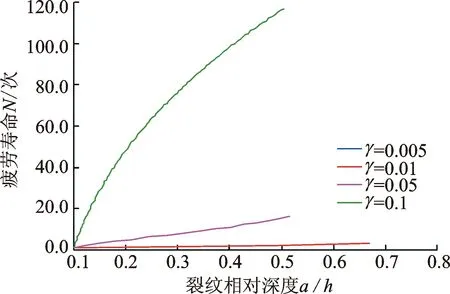
图4 共振状态下，不同阻尼时该裂纹梁的疲劳寿命Fig.4 Fatiguelives of the cracked beam with different damping loss factors at resonance conditions

由图4可见，阻尼损耗因子对共振情况下裂纹梁的疲劳寿命影响非常大。其中当阻尼损耗因子为γ=0.005和γ=0.01时，裂纹梁的疲劳寿命曲线出现重合，因此只显示γ=0.01时的曲线。随着阻尼损耗因子的逐渐减小，该裂纹梁的共振疲劳寿命逐渐较小。与文献[12]得到的结论相同，同时图4与文献[12]中的图3基本相同，只是在疲劳寿命的数值上有很小的误差。因此，可以证明笔者提出的多裂纹梁疲劳寿命预测的方法是可行的。

4.3.2 共振状态下裂纹条数对梁疲劳寿命的影响

假设裂纹的条数、相对位置和深度与4.1.1节完全相同，若该裂纹梁始终处于共振状态下，得到疲劳寿命值列入表3中。

表3 共振状态下裂纹条数不同时裂纹梁的振动疲劳寿命

Tab.3 Fatigue lives of the beam with different number of cracks at resonance conditions 次

表3的数据显示，固定裂纹梁上第1条裂纹的相对位置和深度，随着裂纹条数的增加，该裂纹梁共振疲劳寿命逐步减小。根据4.2节的结论，随着裂纹条数的增加，裂纹尖端应力强度因子逐步增大，由式(25)可以得到每循环的裂纹增量也相应增大，导致疲劳寿命逐步减小。由于第1条裂纹尖端的应力强度因子的值最大，所以第1条裂纹决定着该裂纹梁的疲劳寿命，表3中，随着第一条裂纹远离悬臂梁的固定端，该裂纹梁的疲劳寿命逐步增大。

4.3.3 激励频率恒定的情况下裂纹条数对梁疲劳寿命的影响

假设裂纹的条数、相对位置和深度与4.1.1节完全相同，外激励频率为远离第1阶固有频率100，500，1 000和1 500 Hz得到的疲劳寿命值列入表4中。

表4 恒定激励频率下不同裂纹条数时裂纹梁的疲劳寿命

Tab.4 Fatigue lives of the cracked beam with different number of cracks under constant excitation frequencies 次

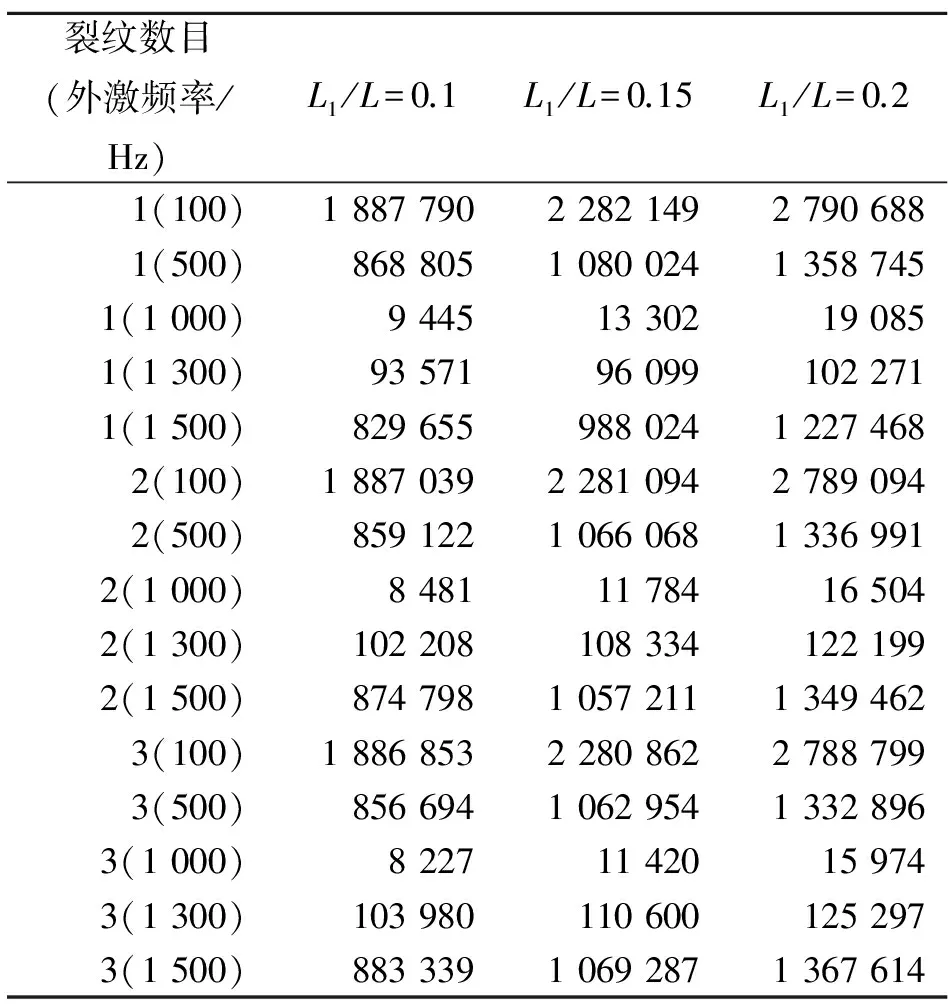
由表4的数据可以得到以下结论。

1) 裂纹梁上第1条裂纹的相对位置决定该梁的疲劳寿命。

2) 在外激励频率恒定的情况下，随着第1条裂纹的相对位置远离该裂纹梁固定端，该梁的疲劳寿命逐步增大。

3) 在外激励频率恒定的情况下，当外激励频率接近第1阶固有频率时，该裂纹梁的疲劳寿命显著减小；当外激励频率远离第1阶固有频率时，该裂纹梁的疲劳寿命显著增大。

4) 在外激励频率小于固有频率的情况下，随着裂纹条数的增加，裂纹梁的固有频率逐步减小，使得此时的外激频率逐步接近固有频率，因而裂纹梁的疲劳寿命逐渐减小；在外激励频率大于固有频率的情况下，随着裂纹条数的加，裂纹梁的固有频率逐步减小，使得此时的外激频率逐步远离固有频率，因而裂纹梁的疲劳寿命逐渐增大。

5 结束语

在含多裂纹的梁上，在固定裂纹梁上某条裂纹的相对位置和深度时，随着裂纹条数的增加，裂纹梁固有频率逐步减小。在含双裂纹的梁上，随着裂纹梁上的任意一条裂纹远离固定端，该裂纹梁固有频率逐步增大；且第1条裂纹(靠近悬臂梁固定端的裂纹)的深度变化对该裂纹梁固有频率的变化影响比较大。

在外激励作用下，当裂纹梁处于共振状态时，固定裂纹悬臂梁上某一裂纹的相对位置和深度，随着裂纹条数的增加，该裂纹尖端应力强度因子的值逐步增大；随着第1条裂纹逐步远离固定端，该裂纹尖端应力强度因子的值逐步减小。在简谐激励作用下，固定裂纹梁上第1条裂纹的相对位置和深度，随着裂纹条数增加，该裂纹梁共振疲劳寿命逐步减小。

在恒定外激励频率小于固有频率的情况下，随着裂纹条数的增加，裂纹梁的固有频率逐步减小，使得此时的外激频率逐步接近固有频率，因而裂纹梁的疲劳寿命逐渐减小；在恒定外激励频率大于固有频率的情况下，随着裂纹条数的增加，裂纹梁的固有频率逐步减小，使得此时的外激频率逐步远离固有频率，因而裂纹梁的疲劳寿命逐渐增大。

[1] Krawczuk M. Natural vibration of rectangular plates with a through crack[J]. Archive Applied Mechanics, 1993, 63(7): 491-504.

[2] Qian Guanliang, Gu Songnan, Jiang Jiesheng. The dynamic behaviour and crack detection of a beam with a crack[J]. Journal of Sound and Vibration, 1990, 138(2): 233-243.

[3] Morassl A. Crack-induced changes in eigen-frequencies of beam structures[J]. Journal of Engineering Mechanics, 1993, 119(9): 1768-1803.

[4] Ostachowicz W M, Krawczuk M.Analysis of the effect of cracks on the natural frequencies of a cantilever beam[J]. Journal Sound and Vibration, 1991, 150(2): 191-201.

[5] Hu Jialou, Liang R Y. An integrated approach to detection of cracks using vibration characteristics[J]. Journal of the Franklin Institute, 1993, 330(5): 841-853.

[6] Shifrin E I, Ruotolo R. Natural frequencies of a beam with an arbitrary number of cracks[J]. Journal of Sound and Vibration, 1999, 222(3): 409-423.

[7] Paris P C, Erdogan F A. Critical analysis of crack propagation laws.[J]. Journal of Basic Engineering, 1963, 85(4):528-534.

[8] 张立军. 宽带随机载荷下的疲劳寿命统一模型[J]. 振动、测试与诊断, 2014, 34(6):1022-1026.

Zhang Lijun. Unified model of fatigue life under wide-band random load[J]. Journal of Vibration, Measurement and Diagnosis,2014,34(6):1022-1026. (in Chinese)

[9] Ponomarev P V, Lopatin A D.Calculation of the fatigue fracture under the influence of dynamic loads [J]. International Applied Mechanics, 1972, 8(6): 613-617.

[10] Shih Y S, Wu G Y. Effect of vibration on fatigue crack growth of an edge crack for a rectangular plate[J]. International Journal of Fatigue, 2002, 24(5): 557-566.

[11] Schlums D H. Fatigue testing and crack analysis of resonating structures[D]. Zürich: Swiss Federal Institute of Technology, 2001.

[12] 刘文光，陈国平.含裂纹悬臂梁的振动与疲劳耦合分析[J].振动与冲击，2011，30(5)：140-144.

Liu Wengguang, Chen Guoping. Coupling analysis for vibration and fatigue of a cracked cantilever beam[J]. Journal of Vibration and Shock, 2011, 30(5): 140-144. (in Chinese)

[13] Dimarogonas A D, Paipetis S A, Chondros T G. Analytical methods in rotor dynamics[M]. London: Applied Publishers, 2013：221-250.

[14] Tada H, Paris P C, Trwin G R. The stress analysis of cracks handbook[M]. Pennsylvania: Del Research Corporation Hellertown, 1973:82-232.

[15] Dentsoras A J, Dimarogonas A D. Resonance controlled fatigue crack propagation in a beam under longitudinal vibration[J]. International Journal of Fatigue, 1983, 23(1): 15-22.

*江苏高校优势学科建设工程基金资助项目(PAPD)

2015-03-26；

2015-05-21

TH114; V224

马一江，男，1989年8月生，博士生。主要研究方向为损伤结构动力学、损伤结构寿命预测。 E-mail:yima@nuaa.edu.cn

陈国平，男，1956年7月生，博士、教授、博士生导师。研究方向为复杂结构动力学。 E-mail:gpchen@nuaa.edu.cn