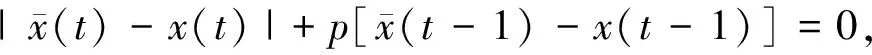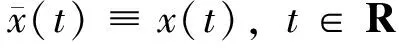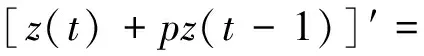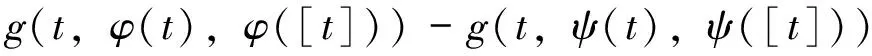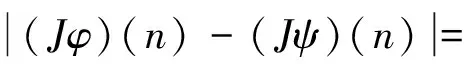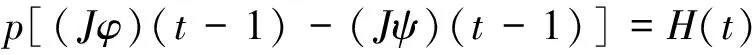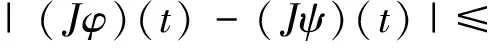Existenceofweightedpseudoanti-periodicsolutionstosomeneutraldifferentialequationswithpiecewiseconstantargument*
,
(1. Department of Mathematics, Guangdong University of Petrochemical Technology, Maoming 525000, China; 2. Department of Mathematics, Huizhou University, Huizhou 516007, China)
Existenceofweightedpseudoanti-periodicsolutionstosomeneutraldifferentialequationswithpiecewiseconstantargument*
LINQuanwen1,ZHUANGRongkun2
(1. Department of Mathematics, Guangdong University of Petrochemical Technology, Maoming 525000, China; 2. Department of Mathematics, Huizhou University, Huizhou 516007, China)
By means of weighted pseudo anti-periodic solutions of relevant difference equations, the existence for weighted pseudo anti-periodic solutions of differential equations with piecewise constant argument is studied. The conditions of existence and uniqueness for the weighted pseudo anti-periodic solutions are presented.
pseudo anti-periodic solutions; pseudo anti-periodic sequences; neutral delay equation; piecewise constant argument
In this paper we consider the following first order neutral delay differential equations with piecewise constant argument of the forms
(1)
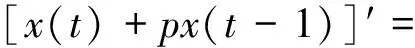
(2)
wherep(≠0),a0,a1areconstants, [·]denotesthegreatestintegerfunction.Tostudytheexistenceofweightedpseudoω-anti-periodic solutions to Eqs. (1) and (2), we will assume that the following assumptions hold:
(H1)f: R→R is weighted pseudoω-anti-periodic function.
(H2)g: R×R2→ R is jointly continuous and satisfiesg(t+ω,x,y) =-g(t,x,y) for allt∈ R and (x,y)∈R2. Moreover, the functiongis uniformly Lipschitz with respect tox,yin the following sense: there existsη> 0 such that
(3)
for all (xi,yi)∈ R2,i=1, 2andt∈R.
A functionx: R → R is called a solution of Eq. (1) if the following conditions are satisfied:
(i)xis continuous on R;
(ii) the derivative ofx(t) +px(t-1)existsonR except possibly at the pointst=n,n∈Z, where one-sided derivatives exist;
(iii)xsatisfies Eq. (1) on each interval (n,n+ 1) , with integern∈Z.
The existence of anti-periodic solutions to differential equations is an attractive topic in the qualitative theory of differential equations due to its applications in control theory or engineering and others, see [1-4] and references therein. Motivated by the study of existence of pseudo almost periodic solutions, and weighted pseudo almost solution to differential equations[5-7], Al-Islam[8]et al. introduced the weighted pseudo anti-periodic functions, which is a natural generalization of the classical pseudo almost periodic functions, and has been used in the investigation of a certain non-autonomous second-order abstract differential equation.
Differential equations with piecewise constant arguments are usually referred to as a hybrid system (a combination of continuous and discrete). These equations have the structure of continuous dynamical systems within intervals and the solutions are continuous, and so combine properties of both differential and difference equations. The equations are thus similar in structure to those found in certain sequential-continuous models of disease dynamics as treated by by Busenberg and Cooke[9]. Therefore, there are many papers concerning the differential equations with piecewise constant argument (see [10-19] and the references therein).
We note that there is no results on the weighted pseudo anti-periodic solution for Eq. (1) (or (2) ) still now. The main purpose of this work is to establish an existence and uniqueness result of weighted pseudo anti-periodic solutions of Eqs. (1) and (2).
1 Preliminary definitions and lemmas
For the sake of convenience, we now state some of the preliminary definitions and lemmas. we always denote byBC(R, R) the space of bounded continuous functionsu: R → R,C(R, R) the space of continuous functionsu: R → R, and denote by |·| the Euclidean norm.
Definition 1 A functionf∈C(R,R) is said to beω-anti-periodic function for someω> 0, iff(t+ω)=-f(t) for allt∈R. The least positiveωwith this property is called the anti-period off.DenotebyAPω(R) the set of all such functions.
Proposition 1 Iff(t) is anω-anti-periodic function, thenf(t) is also (2ω+1) -anti-periodic and 2ω-periodic.
LetUbe the collection of functions (weights)ρ: R → (0, +∞), which are locally integrable over R. Ifρ∈U, we set
and
Obviously,UB⊂U∞⊂U,withstrictinclusions.
Letρ1,ρ2∈U∞,ρ1issaidtobeequivalenttoρ2,denotingthisasρ1ρ2, ifρ1/ρ2∈UB.ThenisabinaryequivalencerelationonU∞(see [7]). Letρ∈U∞,c∈R, defineρcbyρc(t)=ρ(t+c)fort∈R. We denote
UT{ρ∈U∞:ρρcfor eachc∈R}
It is easy to see thatUTcontainsplentyofweights,say, 1, et, 1 + 1/(1 +t2), 1 + |t|nwithn∈N, etc.
Forρ∈U∞,theweightedergodicspacePAP0(R,ρ)isdefinedby
Lemma 1[14]PAP0(R,ρ)withρ∈UTistranslationinvariant,i.e.φ∈PAP0(R,ρ)ands∈Rimplythatφ(·-s)∈PAP0(R,ρ).
Definition 2[7]Letρ∈U∞. A functionf∈BC(R, R) is called weightedω-anti-periodic function (orρ-pseudoω-anti-periodic function) for someω> 0, iffcanbewrittenasf=fap+fe, wherefap∈APω(R), andfe∈PAP0(R,ρ).fapandfeare called theω-anti-periodic component and the weighted ergodic perturbation, respectively, of the functionf. Denote byPAPω(R,ρ)thesetofallsuchfunctions.
Definition 3 Letρ∈U∞.Afunctiong∈BC(R×R)is called weighted pseudoω-anti-periodic function (orρ-pseudoω-anti-periodic function) intuniformly on R2,ifgcan be written asg=gap+ge, wheregapisω-anti-periodic in t uniformly for R2, and for any compact setW⊂R2,geiscontinuous,boundedandsatisfies
uniformlyin(x,y)∈W,gapandgearecalledtheω-anti-periodic component and the weighted ergodic perturbation, respectively, of the functiong.DenotebyPAP(R×R,R,ρ)thesetofallsuchfunctions.
Definition 4 A sequencex: Z → R, denoted by {x(n)}, is called aω-anti-periodic sequence ifx(n+ω)=-x(n) for alln∈Z.We denote the set of all such sequences byAPωS(R).
LetUsdenote the collection of sequences (weights)Q:Z→(0,+∞).ForQ∈UsandT∈Z+={n∈ Z:n≥ 0}, set
Denote
and
UsB
LetQ1,Q2∈Us∞,Q1issaidtobeequivalenttoQ2,denotingthisasQ1Q2,if{Q1(n)/Q2(n)}n∈z∈UsB.ThenitiseasytoseethatisabinaryequivalencerelationonUs∞.LetQ∈Us∞,k∈Z,defineQkbyQk(n)=Q(n+k)forn∈Z.Wedenote
ForQ∈Us∞,theweightedergodicsequencesspacePAP0S(R,Q)isdefinedby
PAP0S(R,Q)
Definition 5 LetQ∈Us∞.Asequencex:Z→R, is called a weighted pseudoω-anti-periodicsequence(orQ-pseudoω-anti-periodicsequence)ifxcanbewrittenasx(n)=xap(n)+xe(n),n∈Zwherexap∈APωS(R), andxe∈PAP0S(R,Q).xapandxearecalledtheω-anti-periodiccomponentandtheweightedergodicperturbation,respectively,ofthesequencex.DenotethesetofallsuchsequencesbyPAPωS(R,Q).
Proposition 2 Iff∈APω(R),ω∈Z+,then{f(n)}n∈Z∈APωS(R).
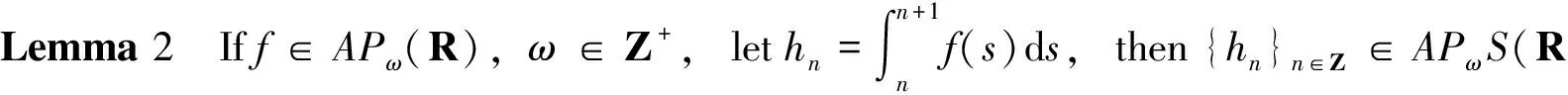
Proof Sincef(t) is anω-anti-periodic function, then for allt∈ R, we havef(t+ω) +f(t) = 0 and
From definition, it follows that {hn}n∈Zisanω-anti-periodic sequence. This completes the proof of Lemma 2.
Lemma 3 Letρ∈UT, and denote
forn∈Z
(4)
ThenQ∈UsT. Moreover, givenc∈R, there exist positive constantsC1,C2such that, for sufficiently largeT,
(5)
Proof Without loss of generality, we assume thatc≥ 0. Sinceρ∈UT,thereexistsM> 0 such thatρc+1(t) ≤Mρ(t) andρ-(c+1)(t) ≤Mρ(t) fort∈ R and
(6)
Notice that
ForT>c+2,i.e.,-T+2c+3 (7) Similarly,wecanprovethatthereexistsM′> 0 such that, forTlarge enough, (8) Thus by (6)-(8), we have forTlarge enough. This leads to (5), and from which we can get easily thatQ∈UsT. The proof is complete. Proposition 3PAP0S(R,Q)withQ∈UsTis translation invariant. This implies that {x(n-k)}n∈Z∈PAP0S(R,Q).Theproofiscomplete. Itisclearthat|hn|≤‖f‖forn∈Zand isω-anti-periodic.Let ForT∈ Z+, we get ForT∈Z+,s∈ [1, 1], let Lemma 5[11]Letx:R→R is a continuous function, andw(t)=x(t)+px(t-1).then t≥t0 Where|p|<1,a=log (1/|p|),b=1/(1-|p|),or t≤t0 Where|p|>1,b=1/(|p|-1). Now,wecanformulateourmaintheorems. Theorem 1 Suppose that (9) Then for anyf∈PAPωS(R,ρ), the following results hold: (i) Ifω=n0∈Z+, Eq. (5) has a uniqueρ-pseudoω-anti-periodic bounded solution. Theorem 2 Suppose that conditions (H2) and (9) hold. Then there existsη*>0,suchthatifη<η*,thatfollowingresultshold: (i)Ifω=n0∈ Z+,Eq. (5)hasauniqueρ-pseudoω-anti-periodic bounded solution. Proof of Theorem 1 (i) Letx(t)beasolutionofEq.(1)onR, integrating (1) fromntot, we have that forn≤t (10) In view of the continuity of a solution at a point, we obtain that fort→(n+1)-0, (11) ThecorrespondinghomogeneousequationofEq. (11)is (12) Following[10],weseektheparticularsolutionsasx(n)=λnforhomogeneousdifferenceequation(12),thenwehavethefollowingcharacteristicequationof(12): (13) Eq. (13)hastwonontrivialsolutions Inviewof(9),wehavethat|λ1,2|≠1andλ1≠λ2,then (14) isthegeneralsolutionsofEq.(12),wherek1,k2are any constants. We define a sequence {cn} by (15) wherek1,k2will be determined later. We put Eq.(15) into Eq.(11) and compare the coefficients ofhn’s. For |λ1|<1, |λ2|<1,weobtainalinearsystemink1andk2 (16) Solving system (16), we have (17) is a solution of the difference equation (11). For other cases we can similarly write out the expression for the solution of Eq.(11). (ii) Sincef∈PAPωS(R,ρ),itfollowsfromLemma4that{hn}n∈Z∈PAPωS(R,Q),sothat{hn} can be written as a sum It is easy to see that Indeed, it is easy to see that forT∈ Z+, Form∈Z+,let FromProposition1,weget (18) Givenε> 0, it is clear that there exists an integerK>0suchthat (19) Thenby(18),thereexistsT0> 0 such that forT>T0, for0≤m≤K (20) Now by (18)-(20), forT>T0we have withx(s)=φ(s),-1≤s≤0. (21) Letw(t)=x(t)+px(t-1),weclaimthatw(t)∈PAP0(R,Q).Letf=fap+fe,wherefap∈APω(R),fe∈PAP0(R,ρ),let Wehave Itfollowsfromdefinitionthatwap(t)isω-anti-periodic. Denote Then {ηn}∈PAP0(R,Q).ByanargumentthesameastheproofLemma4wegetthat Meanwhile,itfollowsfromLemma3thatthereexistssomeM> 0 such thatμs([T] + 1,Q) ≤Mμ(T,ρ) forTlarge enough. Then forTlarge enough we have asT→∞ Thisimpliesthatwe∈PAP0(R,ρ),andhencew∈PAPω(R,ρ). Nextweexpressxin terms ofwand then prove thatx∈PAPω(R,ρ).From Onehasforalln∈Z+ (22) hence, It follows Conversely, if we put xis well defined andwis bounded and |p|<1,xisboundedwith|x(t)| ≤ ‖w(t)‖∞/(1-|p|),moreoveronehas For|p|<1,rewriting(22)as wededuceinasimilarmannerthat If|p|<1,givenε> 0, there exists an integerK> 0 such that (23) Let By a standard argument we can get thatxap∈APω(R). SincePAP0(R,ρ)withρ∈UTis translation invariant, namelyφ∈PAP0(R,ρ)ands∈Rimplythatφ(·-s)∈PAP0(R,ρ) (see[14,Lemma4.1]),wegetthatwe(· -n)∈PAP0(R,ρ)forn∈Z+. So there existsT0> 0 such that forT>T0, for0≤n≤K (24) Now by (23) and (24), forT>T0, This implies thatxe∈PAP0(R,ρ), andx∈PAPω(R,ρ). If |p|>1,let Similarlytotheabove,wecanprovethatx∈PAPω(R,ρ). ∀t∈R Clearly,wehave Fromtheboundednessoftheρ-pseudoω-anti-periodic function, it follows that This means that theρ-pseudoω-anti-periodic solution of Eq. (1) is unique. Proof of Theorem 2 (i) It is easy to seen that the spacePAPω(R,ρ)isaBanachspacewithsupremumnorm‖φ‖=supt∈R|φ(t)|.Foranyφ∈PAPω(R,ρ),usingboth(H2)andthecompositionoffunctionsinPAP0(R,ρ) (seeDiagana[19]),itfollowsthatg(t,φ(t),φ([t]))∈PAPω(R,ρ). Weconsiderthefollowingequation: (25) FromTheorem1,itfollowsthatforanyφ∈PAPω(R,ρ), Eq. (25) has a unique weighted pseudo-anti-ω-periodic solution, denote byJφ. Thus, we obtain a mappingJ:φ→xφ,itfollowsthatJis a mapping fromPAPω(R,ρ)intoitself.Foranyφ,ψ∈PAPω(R,ρ),Jφ-Jψsatisfiesthefollowingequation: where ThisimpliesthatthereexistsK0> 0, such that ∀n∈Z Let ThusthereexistsK1> 0 such that We easily conclude that We typically consider the case when |p|<1.UsingLemma5,wehave wherea=log(1/|p|),b=1/(1-|p|). Settingt0→∞,weobtain Hence,thereexistsη*>0, such that if 0≤η<η*,J:PAPω(R,ρ)→PAPω(R,ρ)iscontractingmapping.Thisimpliesthatthereexistsφ∈PAPω(R,ρ)suchthatJφ=φthatis,Eq. (1)hasauniqueρ-pseudoω-anti-periodic solution. (ii) Ifω=(n0/m0)(n0,m0∈Z+)andgisρ-pseudoω-anti-periodic int, theng(t,φ(t),φ([t]))isaρ-pseudom0ω-anti-periodicfunction,foranyφ∈PAPm0 ω(R,ρ).Atthistime,itfollowsthatEq. (25)hasauniqueρ-pseudom0ω-anti-periodicsolutionJφbyusingTheorem1.Similarly,weknowthatthereexistsη*>0suchthatif0≤η<η*,Eq.(1)hasauniqueρ-pseudom0ω-anti-periodic solution. This completes the proof of Theorem 2. [1] OKOCHI H. On the existence of periodic solutions to nonlinear abstract parabolic equations [J]. J Math Soc Japan, 1988, 40 (3): 541-553. [2] AIZICOVICI S, MCKIBBEN M, REICH S. Anti-periodic solutions to nonmonotone evolution equations with discontinuous nonlinearities [J]. Nonlinear Anal, 2001, 43:233-251. [3] CHEN Y, NIETO J J, O’REGAN D. Anti-periodic solutions for fully nonlinear first-order differential equations [J]. Math Comput Model, 2007, 46:1183-1190. [4] CHEN T, LIU W, ZHANG J, et al. The existence of anti-periodic solutions for Linard equations [J]. J Math Study, 2007, 40:187-195 (in Chinese). [5] ZHANG C Y. Pseudo almost periodic solutions of some differential equations [J]. J Math Anal Appl, 1994, 181: 62-76. [6] ZhANG C Y. Pseudo-almost periodic solutions of some differential equations II [J]. J Math Anal Appl, 1995, 192 (2) : 543-561. [7] DIAGANA T. Weighted pseudo-almost periodic functions and applications [J]. C R Acad Sci Paris, Ser I, 2006,343 (10): 643-646. [8] Al-ISLAM N S, ALSULAMI S M, DIAGANA T. Existence of weighted pseudo anti-periodic solutions to some non-autonomous differential equations [J]. Applied Mathematics and Computation, 2012, 218: 6536-6548. [9] BUSENBERG S, COOK K L. Models of vertically transmitted diseases with sequential-continuous dynamics [M]∥LAKSHMIKANTHAM V, ed. Nonlinear Phenomena in Mathematical Sciences. New York: Academic Press, 1982. [10] COOK K L, WIENER J. A survey differential equation with piecewise continuous argument [M]∥BUSENBERG S, MARTELLI, eds. Lecture Notes in mathematics, Vol. 1475. Berlin: Springer, 1991:1-15. [11] YUAN R. On the existence of almost periodic solutions of second order delay differential equations with piecewise constant argument [J]. Sci China, 1998, 41(3): 232-241. [12] YUAN R. Pseudo-almost periodic solutions of second order neutral delay differential equations with piecewise constant argument [J]. Nonlinear Anal, 2000, 41: 871-890. [13] ZHAN R L L, LI H X. Weighted pseudo-almost periodic solutions for some abstract differential equations with uniform continuity [J]. Bull Aust Math Soc, 2010, 82: 424-436. [14] ZHANG L L, LI H X. Weighted pseudo-almost periodic solutions of second order neutral differential equations with piecewise constant argument [J]. Nonlinear Anal, 2011,74: 6770-6780. [15] ZHUANG R K, YUAN R. The existence of pseudo-almost periodic solutions of third-order neutral differential equations with piecewise constant argument [J]. Acta Math Sin (Engl Ser), 2013,29(5): 943-958. [16] ZHUANG R K, YUAN R. Weighted pseudo almost periodic solutions of N-th order neutral differential equations with piecewise constant arguments [J]. Acta Math Sin (Engl Ser), 2014,30(7): 1259-1272. [17] ZHANG L, XU Y. Existence of almost periodic solutions for some nonlinear Duffing equations [J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2010, 49(4): 6-10. [18] ZHANG L. Almost periodic mild solutions to functional differential equations of neutral type in Banach space [J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2016, 55(1): 30-34. [19] DIAGANA T. Pseudo almost periodic functions in Banach spaces [M]. New York: Nova Science Publishers Inc, 2007. 2017-02-22 基金项目:国家自然科学基金(11271380,11501238) ;广东省自然科学基金(2014A030313641,2016A030313119);广东省教育厅重大项目基金(2014KZDXM070) 林全文(1965年生),男;研究方向:微分方程与动力系统;E-mail:linquanwen@126.com O175 A 0529-6579(2017)03-0057-09 具有分段常变量的中立型微分方程加权伪反周期解的存在性 林全文1,庄容坤2 (1. 广东石油化工学院数学系,广东 茂名 525000; 2. 惠州学院数学系,广东 惠州 516007) 通过构造差分方程的加权伪反周期解,研究了一类含分段常变量中立型微分方程的加权伪反周期解的存在性,给出了所论方程的加权伪反周期解的存在唯一性条件。 伪反周期解;伪反周期序列;中立型时滞方程;分段常变量 10.13471/j.cnki.acta.snus.2017.03.009

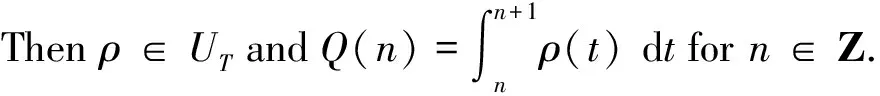

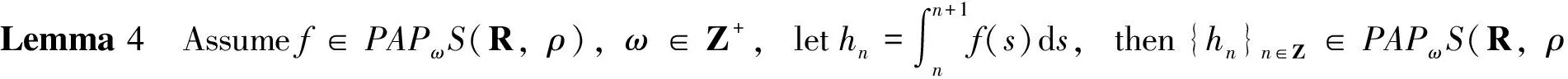
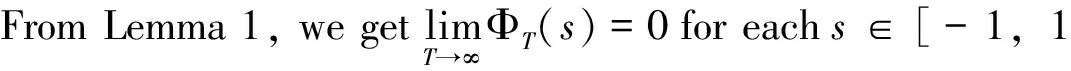
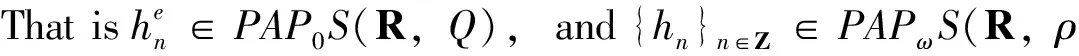
2 Main results
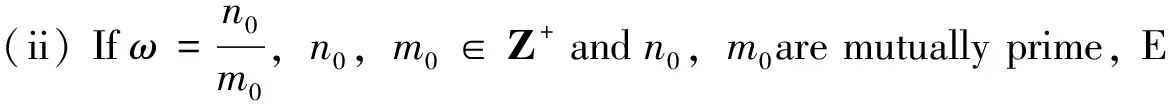
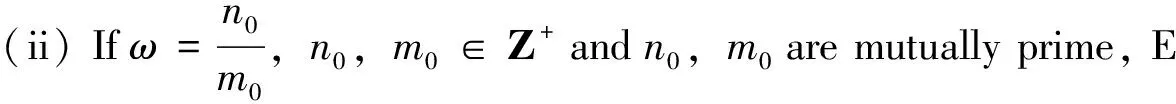
3 Proofs of theorems