聚焦圆锥曲线的新颖题型

■陕西洋县中学 何记英 刘大鸣(特级教师)

聚焦圆锥曲线的新颖题型

■陕西洋县中学 何记英 刘大鸣(特级教师)

圆锥曲线的新颖题型主要有：定义的巧用,离心率的求解,焦点三角形的面积,焦点弦长问题,轨迹方程的探究,直线与圆锥曲线的位置关系,以及证明定值、求定点和相关最值等。求解时常用到设而不解、整体思维,有时还要用到平面几何的基本知识和向量的基本方法。

聚焦一 用圆锥曲线定义探求几何量

例1 (2 0 1 6年吉林省实验中学高三质检)如图1,过双曲线的左焦点F1,作圆x2+ y2=a2的切线交双曲线右支于点P,切点为T, P F1的中点M在第一象限,则以下结论正确的是( )。

A.b-a=|MO|-|MT|

B.b-a＞|MO|-|MT|

C.b-a＜|MO|-|MT|

D.b-a=|MO|+|MT|

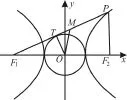
图1

解析：因为T为切点,则O T⊥P F1。在R t△O T F1中,|T F1|=b,连接P F2,由三角形中位线定理可得+b=b-a。选A。

点评：解决本题的关键是用O T⊥P F1和几何量的关系求出|T F1|=b。由中位线定理得,再结合双曲线的定义最终求出答案。

聚焦二 构建不等关系求圆锥曲线离心率的取值范围

例2 (浙江省宁波市效实中学2 0 1 6年上学期期中测试)已知F1、F2分别为的左、右焦点,P为双曲线右支上任一点,若的最小值为8a,则该双曲线的离心率的取值范围是。

解析：借助双曲线的定义,再降元,以及运用基本不等式解题。欲取到最小值8a,则|P F2|=2a,而|P F2|≥c-a,即2a≥c-a,所以1＜e≤3。

点评：求离心率的值或取值范围,常依据题设条件构造a、c的齐二次式,以及借助基本不等式、平面几何性质和曲线本身范围构建a、c的不等关系式,本题中构建a、c满足的不等关系时既用到基本不等式取等号的条件,又用到了双曲线上任一点到其对应焦点的距离不小于c-a的几何性质。

聚焦三 焦点三角形面积问题

例3 (四川省绵阳市南山中学2 0 1 6学年上学期期中测试)双曲线(n＞1)的两焦点为F1、F2,点P在双曲线上,且满足|P F1|+|P F2|=2,则△P F1F2的面积为( )。

解析：假设点P在右支上,由双曲线定义可知|P F1|-|P F2|=2。

又因为|P F1|+|P F2|=2n+2,所以|P F1|=n+2+n,|P F2|=n+2-n。

因为|F1F2|=2n+1,所以|P F1|2+ |P F2|2=|F1F2|2,△P F1F2的面积=1,故选A。

点评：求双曲线或椭圆的焦点三角形面积,主要用到余弦定理和双曲线或椭圆的定义以及面积公式这些知识点。若点P为椭圆上非顶点的任一点,(a＞b＞0)的两焦点,则=∠F1P F2。对于双曲线其中θ=∠F1P F2。

聚焦四 与抛物线焦点弦长有关的问题

例4 (2 0 1 6年辽宁省五校高三上学期联考)如图2,设抛物线y2=4x的焦点为F,直线l过F且与C交于A、B两点。若|A F|=3|B F|,则直线l的斜率为。

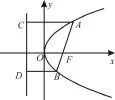
图2

点评：已知抛物线y2=2p x(p＞0),过其焦点的直线交抛物线于A、B两点(如图2所示),设A(x1,y1),B(x2,y2),用方程研究有以下结论：

(1)|A B|=x1+x2+p。

(2)x1x2=

(3)以A B为直径的圆与抛物线的准线相切。

(4)抛物线的通径长为2p,是过焦点的弦长的最小值。

(5)以A F或B F为直径作圆,则此圆与y轴相切。

聚焦五 代入法求动点的轨迹方程

例5 (2 0 1 6年江苏省南京市模拟卷)如图3,P是椭圆=1上的任意一点,F1、F2是它的两个焦点,O为坐标原点

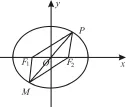
图3

则动点Q的轨迹方程是。

点评：如果动点Q(x,y)依赖于另一动点P(x0,y0)(即相关点),而点P(x0,y0)又在某一已知曲线上运动,则可根据向量关系、坐标关系列出关于x0,y0,x,y的方程组,利用x,y表示出x0,y0,再把x0,y0代入已知曲线方程,便可得出动点Q(x,y)的轨迹方程。这种方法是代入法。

聚焦六 定义法探究立体几何和解析几何交汇的轨迹方程

例6 如图4,正方体A B C D-A1B1C1D1的棱长为1,点Μ在棱Α B上,且,点P是平面A B C D上的动点,且动点P到直线A1D1的距离与点Ρ到点Μ的距离的平方差为1,则动点Ρ的轨迹是( )。

A.圆 B.抛物线

C.双曲线 D.直线

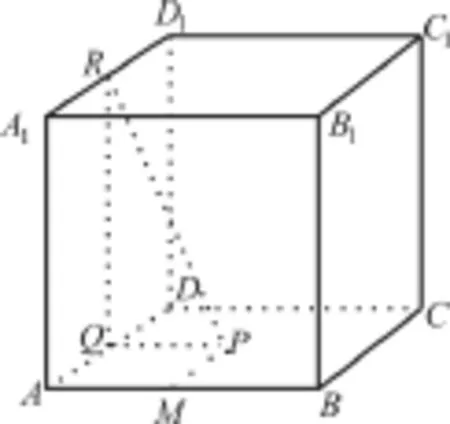
图4

解析：如图4所示,过点P作P Q⊥A D,垂足为Q,则P Q⊥平面A DD1A1。过点Q作Q R⊥A1D1,垂足为R,则A1D1⊥平面P Q R,故P R⊥A1D1。

P R即为点Ρ到直线A1D1的距离,则P R2-P Q2=R Q2=1。又已知P R2-PM2=1,故P Q=PM。由抛物线的定义可知动点Ρ的轨迹是抛物线。

点评：求解立体几何和平面几何交汇的动点轨迹问题,关键在于利用空间概念合理转换为平面内圆锥曲线的定义。为了得到P Q=PM,将已知条件中“动点Ρ到直线Α1D1的距离与点Ρ到点Μ的距离的平方差为1”用数学语言表达,即作出点P到线和面的距离进行转化。

聚焦七 参数法探求动点的轨迹方程

例7 (2 0 1 5年广东卷理)已知过原点的动直线l与圆C：x2+y2-6x+5=0相交于不同的两点A、B。求线段A B的中点M的轨迹方程。

解析：设A(x1,y1),B(x2,y2),过原点的动直线为l：y=k x,将动直线l代入圆C：x2+y2-6x+5=0,消去y得(k2+1)x2-6x+5=0。因为Δ=3 6-2 0(1+k2)＞0,所以。设中点为M(x,y),则x1+x2=除得到。代入消去k,得：

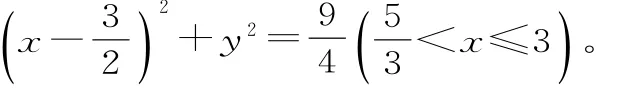
点评：如果直接找不出动点的横坐标x与纵坐标y之间的关系,则可借助中间变量(参数可能不止一个)使x,y之间建立起联系,然后再从所求式子中消去参数,得出动点的轨迹方程。注意题设参数隐含的范围对横纵坐标的限制,如本题由x≤3。

聚焦八 直线和圆锥曲线的位置关系

例8 (吉林省实验中学2 0 1 5-2 0 1 6学年上学期期中测试)若双曲线1(a＞0)的离心率等于2,直线y=k x-1与双曲线E的右支交于A、B两点。

(1)求k的取值范围;

设A(x1,y1),B(x2,y2),由得(1-k2)x2+2k x-2=0。①

整理得2 8k4-5 5k2+2 5=0,解得k2=

设C(x3,y3),由(x3,y3)=m(x1+x2,y1+y2)=(45m,8m)。

因为点C是双曲线上一点,

所以8 0m2-6 4m2=1,解得

点评：设出直线方程或双曲线方程,联立消元后转化成关于x或y的一元二次方程,利用根与系数的关系时,注意曲线的范围和两个交点的隐含条件,构建不等式组求参数范围或整体代入求解弦长的有关问题。

聚焦九 点差法探究圆锥曲线的中点弦或对称问题

例9 (2 0 1 5年高考四川卷理科)如图5,设直线l与抛物线y2=4x相交于A、B两点,与圆(x-5)2+ y2=r2(r＞0)相切于点M,且M为线段A B的中点。若这样的直线l恰有4条,则r的取值范围是( )。

图5

A.(1,3) B.(1,4) C.(2,3) D.(2,4)

解析：显然当直线l的斜率不存在时,必有两条直线满足题设条件。当直线l的斜率存在时,设斜率为k。设A(x1,y1),B(x2, y2),x1≠x2,M(x0,y0),则相减得(y1+y2)(y1-y2)=4(x1-x2)。由于x1≠ x2,所以,即k y0=2。圆心为C(5,0),由CM⊥A B得=-1,k y0=5-x0,所以2=5-x0,x0=3,即点M必在直线x=3上。将x=3代入y2=4x得y2=1 2,故-23＜y0＜23。

因为点M在圆(x-5)2+y2=r2(r＞0)上,所以(x0-5)2+y02=r2,r2=y02+4＜1 2 +4=1 6。又y20+4＞4(由于斜率不存在,故y0≠0,不取等号),所4＜y20+4＜1 6,故2＜r＜4。选D。

点评：凡涉及弦的中点或曲线上存在两点关于直线对称问题,常常采用“点差法”将弦的斜率用中点的坐标表示。

聚焦十 巧用定义和三点共线的条件求最值

例1 0 (河北省唐山一中2 0 1 6年上学期期中考试)已知双曲线的左、右焦点分别为F1、F2,P为双曲线左支上一点, M为双曲线渐近线上一点(渐近线的斜率大于零),则|P F2|+|PM|的最小值为。

解析：焦点F1(-4,0),F2(4,0),符合题意的渐近线方程为

由双曲线的定义可知|P F2|-|P F1|= 2a=21 4,所以|P F2|+|PM|=|P F1|+ |PM|+21 4。

作出符合题意的几何图形如图6所示,由图形可知|P F1|+ |PM|≥|F1M|,所以当F1、P、M三点共线时, |P F1|+|PM|的值最小,依据点F1(-4,0)到直线的距离公式可得此时的最小值为,故所求的最小值为21 4+2。

图6

点评：应用曲线的定义及几何意义求值、求最值等问题在抛物线中很常见,这里列举了双曲线的问题,可见知识的应用可以拓展。

聚焦十一 构建一元目标函数求最值

例1 1 (2 0 1 6年山东省淄博市一模)已知椭圆C：x2+2y2=2。F1、F2分别是椭圆的左、右焦点,过F2的直线交椭圆于M、N两点,求的最小值和最大值。

解析：易知右焦点F2(1,0),若直线MN的斜率不存在,则

若直线MN的斜率存在,设MN的方程为y=k(x-1)。设M(x1,y1),N(x2,y2),得(2k2+1)x2-4k2x+2k2-2=0。由题设知恒有两个交点,所以x1+

点评：“过点F2的直线”提示我们用直线为点斜式做题比较方便,既然引入了变量k,目标可以通过韦达定理转化为含k的一元一次分式函数,从而用函数观点求最值。为了避免讨论斜率还可设“过点F2的直线为x=m y+1”。

聚焦十二 构建二元目标函数求最值

例1 2 动点Q在椭圆C：2x2+y2=5上移动。两定点为求△A B Q的面积取最大值时点Q的坐标。

解析：设点Q(x0,y0),则有2x20+y20= 5。直线A B的方程为x+2y=0,则点Q到A B的距离

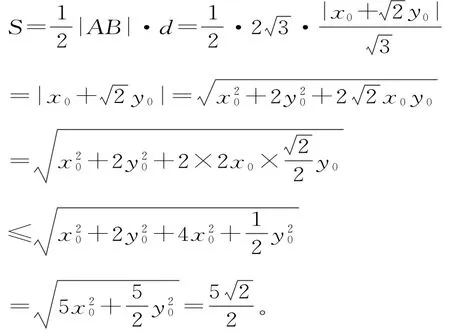
点评：设出动点Q的坐标后,将目标转化为二元函数,可以不消元,利用基本不等式,再结合=5求解。

聚焦十三 通过特殊情况猜想并证得定点或定值

解析：由m+k=0知m=-k,直线l的方程可化为y=k(x-1)。

设M(x1,y1),N(x2,y2),则：

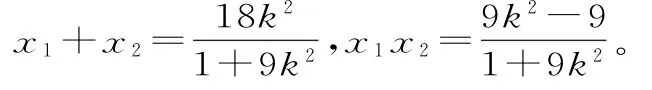
点评：对于探索性问题,我们可先特殊化处理,猜想问题的存在性,再作一般性的证明。这样处理能为探究提供具体的方向,减少运算量。如本题中取k=1探究使问题简单明朗化。

(责任编辑 徐利杰)