涤尽铅华，返璞归真
——看正、余弦定理在实际中的应用

■河南省许昌市第二高级中学 张军志

涤尽铅华，返璞归真
——看正、余弦定理在实际中的应用

■河南省许昌市第二高级中学 张军志

现实生活中,存在大量的对距离、高度、角度等问题的研究,褪去其载体,对于其表面的实际情景,则可抽象为对三角形的求解问题。借助于正、余弦定理,可对这些实际问题加以研究和解决。

问题一:测量距离问题

距离问题的解法:研究测量距离问题时,要选取合适的辅助测量点,构造三角形,将问题转化为求某个三角形的边长问题,从而利用正余弦定理求解。

图1

如图1,在一条海防警戒线上的点A,B,C处各有一个水声监测点,B,C两点到A的距离分别为20km和50km,某时刻,B收到发自静止目标P的一个声波信号,8s后A,C同时接收到该声波信号,声波在水中的传播速度是1.5km/s。

(1)设A到P的距离为xkm,用x表示B、C到P的距离,并求x的值;

(2)求P到海防警戒线AC的距离。

解:(1)依题意,有PA=PC=x,PB=x-1.5×8=x-12。

(2)作PD⊥AC于点D,在△ADP中,由cos∠PAD=得sin∠PAD=PAsin∠PAD=

如图2,已知在东西方向上有M、N两座小山,山顶各有一个发射塔A、B,塔顶A、B的海拔分别为AM=100m和BN=200m,一测量车在小山M的正南方向的点P处测得发射塔顶A的仰角为30°,该测量车向北偏西60°方向行驶了1003m后到达点Q,在点Q处测得发射塔顶B的仰角为θ,且∠BQA=θ,经测量tanθ=2,求两发射塔顶A、B之间的距离。

图2

解:在Rt△AMP中,∠APM=30°,AM=100,则PM=1003,连接QM,在△PQM中,∠QPM=60°,又PQ=1003,故△PQM为等边三角形,QM=1003。

在Rt△AMQ中,由AQ2=AM2+QM2,得AQ=200。

在Rt△BNQ中,tanθ=2,BN=200,故BQ=100cosθ=

在△BQA中,BA2=BQ2+AQ2-2BQ

点评:求距离问题时注意:选定或确定要创建的三角形,首先确定所求量所在的三角形,若其他量已知则直接求解;若有未知量,则把未知量放在另一确定的三角形中求解。

问题二:解决高度问题

对于高度问题一般是把它转化成三角形的问题,求解时要注意三角形中的边角关系的应用,若是空间的问题要注意空间图形和平面图形的结合。

(2015·湖北高考)如图3,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧一山顶D在西偏北30°的方向上,行驶600m后到达B处,测得此山顶在西偏北75°的方向上,仰角为30°,则此山的高度CD=____m。

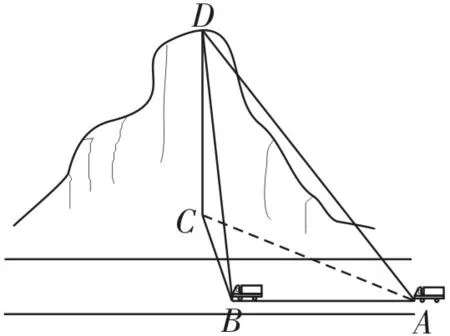
图3

解:由题意,在△ABC中,∠BAC=30°,∠ABC=180°-75°=105°,故∠ACB=45°。

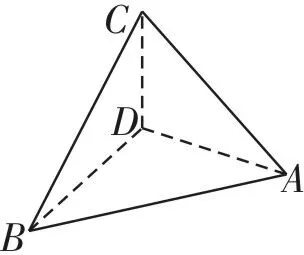
图4

如图4,为了估测某塔的高度,在同一水平面的A、B两点处进行测量。在点A处测得塔顶C在西偏北20°的方向上,仰角为60°;在点B处测得塔顶C在东偏北40°的方向上,仰角为30°。若A、B两点相距130m,则塔的高度CD=

解:分析题意可知,设CD=h,则AD=BD=在△ADB中,∠ADB=180°-20°-40°=120°,由余弦定理AB2=BD2+AD2-2BD·AD·cos120°,可得1302=3h2+解得h=10故塔的高度为10

点评:求解高度问题时注意:(1)在测量高度时,理解仰角、俯角(它是在铅垂面上所成的角)、方向(位)角(它是在水平面上所成的角)是关键;(2)在实际问题中,可能会遇到空间与平面(地面)同时研究的问题,这时最好画两个图形,一个空间图形,一个平面图形,这样处理起来既清楚又不容易搞错;(3)注意山或塔垂直于地面或海平面,把空间问题转化为平面问题。

问题三:测量角度问题

求解测量角度问题的关键是在弄清题意的基础上,画出表示实际问题的图形,并在图形中标出有关的角和距离,再用正弦定理或余弦定理解三角形,最后将解得的结果转化为实际问题的解。

在一次海上联合作战演习中,红方一艘侦察艇发现在北偏东45°方向,相距12nmile的水面上,有蓝方一艘小艇正以每小时10nmile的速度沿南偏东75°方向前进,若红方侦察艇以每小时14nmile的速度,沿北偏东45°+α方向拦截蓝方的小艇。若要在最短的时间内拦截住,求红方侦察艇所需的时间和角α的正弦值。

图5

解:如图5,设红方侦察艇经过xh后在C处拦住蓝方的小艇,则AC=14x,BC=10x,∠ABC=120°。

根据余弦定理得(14x)2=122+(10x)2-240xcos120°,解得x=2。

故AC=28,BC=20。

图6

如图6,位于A处的信息中心获悉:在其正东方向相距40nmile的B处有一艘渔船遇险,在原地等待营救。信息中心立即把消息告知在其南偏西30°、相距20nmile的C处的乙船,现乙船朝北偏东θ的方向沿直线CB前往B处救援,求cosθ的值。

解:在△ABC中,AB=40,AC=20,∠BAC=120°,由余弦定理得,BC2=AB2+AC2-2AB·AC·cos120°=2800⇒BC=207。

由∠BAC=120°,知∠ACB为锐角,则cos∠ACB=

由θ=∠ACB+30°,得cosθ=cos(∠ACB+30°)=cos∠ACBcos30°-sin∠ACBsin30°=

点评:解决测量角度问题时,要明确方位角及方向角的含义,方位角是指北方向线与目标方向线按顺时针之间的夹角,而方向角是正北或正南方向线与目标方向线所成的锐角。

通过以上常见正、余弦定理在解实际问题中的应用,我们可概括其一般的解题步骤为:第一步,分析——理解题意,分清已知与未知,画出示意图,并标出条件;第二步,建模——根据已知条件与求解目标,把已知量与求解量尽量集中在有关的三角形中,建立一个解斜三角形的数学模型;第三步,求解——利用正弦定理或余弦定理有序地解出三角形,求得数学模型的解;第四步,检验——检验上述所求的解是否符合实际意义,从而得出实际问题的解。

(责任编辑 徐利杰)