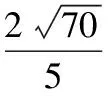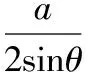几何题组训练
——立体几何的计算

四川 陈晓芳

广东 卜大海

辽宁 李海武

江苏 王怀学

几何题组训练
——立体几何的计算

四川 陈晓芳

广东 卜大海

辽宁 李海武

江苏 王怀学

1 公式法求几何体的体积和表面积

1.1几何体的侧面积与表面积

【典例1】(1)若一个圆锥的侧面展开图是一个半径为3 cm,圆心角为60°的扇形，则该圆锥的侧面积和体积分别为________.

【解析】(1)如图，PA=3 cm,∠BPA=60°，设OA=r，

所以，该圆锥的体积为

【变式1】一个高为2的圆柱，底面周长为2π，该圆柱的表面积为________．

【变式2】边长为1的正方形的一边所在直线为旋转轴，将该正方形旋转一周所得圆柱的侧面积等于

( )

A．2π B．π C．2 D．1

【变式3】用一张4 cm×8 cm的矩形硬纸卷成圆柱的侧面，则轴截面的面积为________(接头忽略不计).

( )

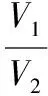
【解析】(1)在正△ABC中，D为BC中点，

因为平面BB1C1C⊥平面ABC,

AD⊥BC,AD⊂平面ABC,

所以AD⊥平面BB1C1C,

即AD为三棱锥A-B1DC1底面上的高.

故选C.

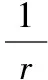
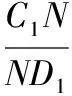
【变式4】Rt△ABC的边长分别是3,4,5，现以斜边AB所在的直线为轴把△ABC(及其内部)旋转一周后，所得几何体的体积是________ ．

1.2 “选准底面，找对高”

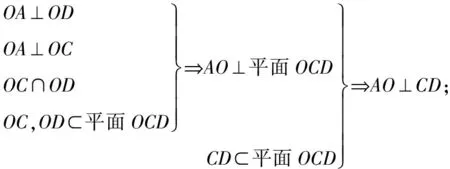
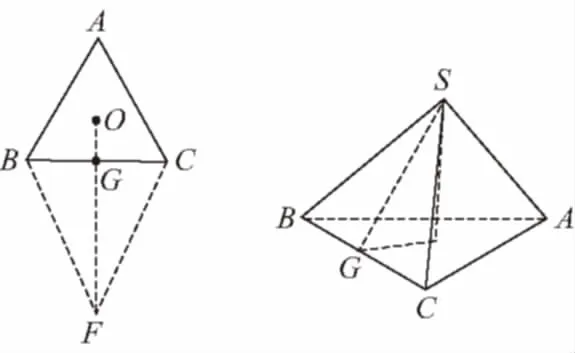
【典例】如图所示，在边长为4的正方形纸片ABCD中，AC与BD相交于O，剪去△AOB，将剩余部分沿OC，OD折叠，使OA，OB重合.

(1)以A，B，C，D，O为顶点的四面体O-ACD是怎样的四面体？

(2)求证：OA⊥CD;

(3)求四面体的体积．

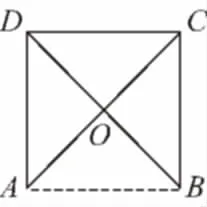
【解析】(1)折叠后的四面体如图所示．OA,OC,OD两两相互垂直，即侧棱两两垂直的三棱锥；

(2)证明:

【变式1】如图所示，在边长为4的正方形纸片ABCD中，E，F分别为边BC，CD的中点.

(1)沿图中虚线折起，使得B，C，D三点重合，此时4个面围成怎样的几何体？

(2)求围成的几何体的体积.

【变式2】如图所示，在边长为4的正方形纸片ABCD中，AC与BD相交于O,剪去△AOB,将剩余部分沿OC，OD折叠，使OA，OB重合，则以A(B)，C，D，O为顶点的四面体的体积为________.

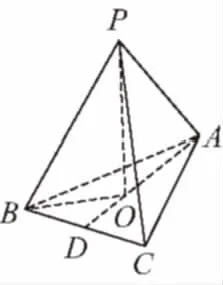
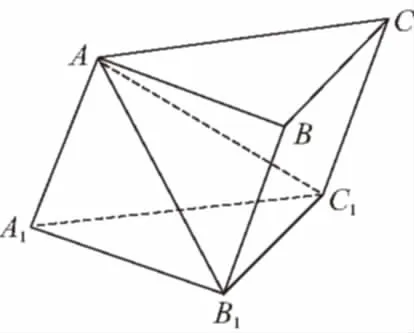
【变式3】如图，在三棱柱ABC-A1B1C1中，CC1⊥底面ABC，AC=BC=CC1=2，AC⊥BC，点D是AB的中点,求四面体B1C1CD的体积．

1.3认清几何体中的相关元素

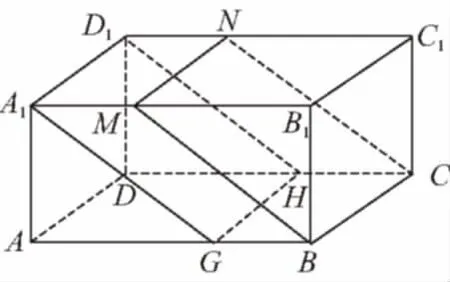
【典例】在直棱柱ABC-A1B1C1中，AB⊥BC,BN⊥CB1,M∈AB.

求证：B1C⊥平面BNM.

【证明】在直棱柱ABC-A1B1C1中，B1B⊥平面ABC，

且AB⊂平面ABC,所以B1B⊥AB.

又AB⊥BC，B1B∩BC=B,B1B,BC⊂平面B1BC,

所以AB⊥平面B1BC,

因为B1C⊂平面B1BC,

所以AB⊥B1C，即MB⊥B1C,

因为MB⊥B1C，NB⊥B1C，MB∩BN=B,

MB,BN⊂平面BNG.

所以B1C⊥平面BNM.

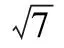
【变式2】一个直角梯形的两底长分别为2和5，高为4，绕其较长的底旋转一周，所得到的几何体的表面积为________.

1.4用直截面法求几何体的体积

【典例】四面体的六条棱中，有五条棱长都等于a，则该四面体的体积的最大值为________.

【解析】如图，在四面体ABCD中，

设AB=BC=CD=AC=BD=a，AD=x，

取AD的中点为P，BC的中点为E，连接BP,EP,CP．

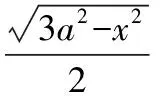
所以VA-BCD=VA-BPC+VD-BPC

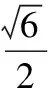
【变式1】已知球的直径SC=4，A,B是该球球面上的两点，AB=2，∠ASC=∠BSC=45°，则棱锥S-ABC的体积为

( )

【变式2】如图，在三棱柱ABC-A1B1C1中，侧棱AA1⊥平面AB1C1，AA1=1，底面△ABC是边长为2的正三角形，求此三棱柱的体积.

1.5用等体积法求体积

【典例1】将边长为1的正方形ABCD沿对角线AC折起，使△ABD为正三角形，则三棱锥A-BCD的体积为

( )

【解析】如图，取AC的中点O,连接BO,DO,

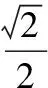
因为△ABD为正三角形,DB=1,DO2+BO2=DB2,

所以DO⊥OB,所以DO⊥平面ABC,

故选D.

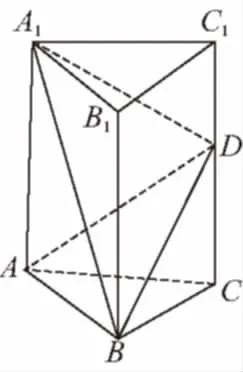
【变式1】如图，直三棱柱ABC-A1B1C1中，各侧棱和底面的边长均为a，点D是CC1上任意一点，连接A1B,BD,A1D,AD，则三棱锥A-A1BD的体积为________．

【变式2】如图，四棱锥P-ABCD中，PA⊥底面ABCD，底面ABCD是矩形，AB=2,AD=3,PA=4，点E为棱CD上一点，则三棱锥E-PAB的体积为________．

【变式3】如图，在长方体ABCD-A1B1C1D1中，AB=BC=1，AA1=2，E是侧棱BB1的中点．

(1)求证：A1E⊥平面ADE；

(2)求三棱锥A1-ADE的体积．

【典例2】如图，正方体ABCD-A1B1C1D1的棱长为1，E，F分别为线段AA1，B1C上的点，则三棱锥D1-EDF的体积为________．

【解析】(法1)三棱锥D1-EDF的体积即为三棱锥F-DD1E的体积．

因为E，F分别为AA1，B1C上的点，

所以在正方体ABCD-A1B1C1D1中，

(法2)将E点平移到A点，将F点平移到C点，

( )

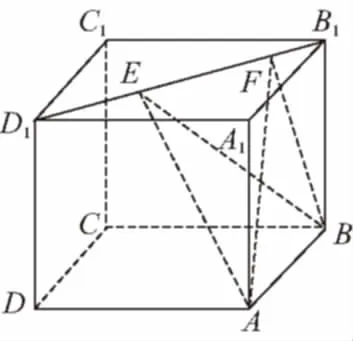
A.AC⊥BE

B.EF∥平面ABCD

C.三棱锥A-BEF的体积为定值

D.△AEF的面积与△BEF的面积相等

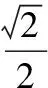
【变式3】如图，在棱长为1的正方体ABCD-A1B1C1D1中,E是棱BC上的一点，则三棱锥D1-B1C1E的体积为________.

2 球的相关计算

2.1球的截面的性质

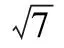
①弦AB，CD可能相交于点M；

②弦AB，CD可能相交于点N；

③MN的最大值为5；

④MN的最小值为1.其中真命题的个数为

( )

A.1个 B.2个

C.3个 D.4个

【解析】当弦AB，CD相交时，则在一个截面圆上，由于ABlt;CD，所以弦AB，CD可能相交于点M，弦AB，CD不可能相交于点N.故①是真命题；②是假命题；

连接OM，ON，当OMN为三角形时，由于OM+ONgt;MN，OM-ONlt;MN，所以，当MN共线且在球心O的不同侧时，MN取得最大值5；当MN共线且在球心O的同侧时，MN取得最小值1.故③④为真命题.

【变式1】已知过球面上三点A，B，C的截面和球心的距离等于球半径的一半，且AB=BC=CA=1，则该球的半径是

( )

【变式2】用与球心距离为1的平面去截球，所得的截面面积为π，则球的体积为

( )

【变式3】过球的一条半径的中点，作垂直于该半径的平面，则所得截面的面积与球的表面积的比为

( )

( )

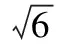
【变式5】一个与球心距离为1的平面截球所得的圆面面积为π，则球的表面积为________．

2.2将三棱锥补形成长方体求外接球的半径

【解析】如图，将正三棱锥补形成正方体，可知球心O为体对角线PD的中点，

设P到平面ABC的距离为h，

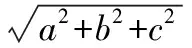
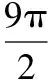
【变式2】正四面体的四个顶点都在同一个球面上，且正四面体的高为4，则这个球的表面积是________．

【变式3】如图，在三棱锥V-ABC中，VA⊥底面ABC,∠ABC=90°,若VA=1,AB=2,BC=3，则三棱锥外接球的表面积为________．

2.3确定球心的位置

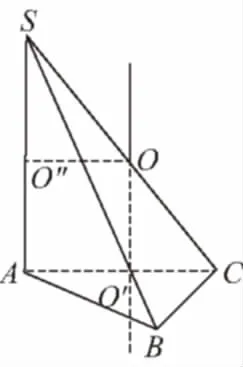
【评注】当球面上有四点P，A，B，C满足PA，PB，PC两两互相垂直时，正三棱锥P-ABC的外接球就是以PA，PB，PC为棱的正方体的外接球，球心在其体对角线的中点处．

从局部看，简单几何体的顶点到其外接球球心的距离是相等的，可以先考虑到一个平面上的点(三个或三个以上)等距离的点的集合，因此可以借助勾股定理、垂径定理、射影定理等计算圆心位置．

( )

【变式2】如图，三棱锥S-ABC中，SA⊥平面ABC，SA=2，△ABC是边长为1的正三角形，则其外接球的体积是________.

【变式4】某球的外切圆台上下底面半径分别为r,R，求该球的体积________.

3 简单几何体中的最值问题

3.1利用运动变化的观点求解几何体的最值

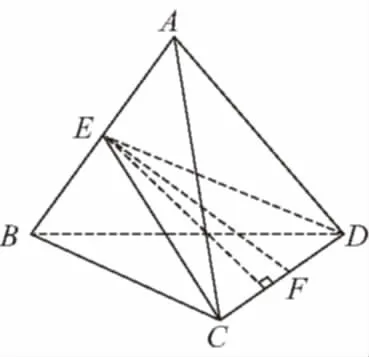
【典例】已知在半径为2的球面上有A,B,C,D四点，若AB=CD=2，则四面体ABCD的体积的最大值为________．

【解析】如图，过CD作平面ECD，

使AB⊥平面ECD，交AB于E，

设点E到CD的距离EF=d，

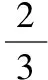
当球的直径通过AB与CD的中点时，

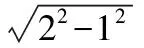
【变式1】三棱锥A-BCD中，AB=BC=CA=BD=CD=1，则该三棱锥体积的最大值为________．

【变式3】在封闭的直三棱柱ABC-A1B1C1内有一个体积为V的球，若AB⊥BC,AB=6,BC=8,AA1=3,则V的最大值是

( )

3.2利用侧面展开图“化曲为直”求距离的最值

【典例1】如图，已知圆锥的底面半径为1，母线SA长为6，M为SA的中点，有一根绳子从A点出发，沿圆锥的侧面绕一周到达M点，问绳子最短是多少？

【解析】沿母线SA将圆锥侧面展开，

AM点分别对应展开图中的A1，M1点，

则在展开图中，线段AM1的长度即为最短绳长.

所以△SA1A是正三角形，

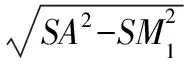
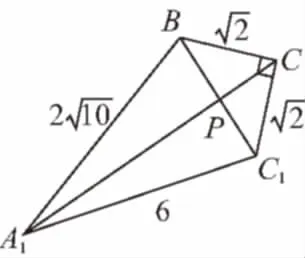
【变式3】如图，已知正三棱柱ABC-A1B1C1的底面边长为1，高为8，一质点自A点出发，沿着三棱柱的侧面绕行两周到达A1点的最短路线的长为________．

3.3利用基本不等式求体积的最值

【典例】(1)已知正六棱柱的12个顶点都在一个半径为3的球面上，当正六棱柱的体积最大(柱体体积=底面积×高)时，其高的值为________.

(2)一个圆柱体的体积是16 πcm,求其表面积的最大值.

【解析】(1)设正六棱柱的底面边长为a，高为2h，

则a2+h2=9，

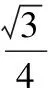
(2)设圆柱体的高为h，底面半径是r，16π=πr2h，

圆柱体的表面积

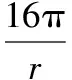
圆柱体的表面积Smax=24π.

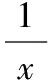
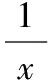
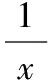
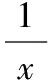
3.4利用导数求体积的最值

【典例1】某商场为促销要准备一些正三棱锥形状的装饰品，用半径为10 cm的圆形包装纸包装．要求如下：正三棱锥的底面中心与包装纸的圆心重合，包装纸不能裁剪，沿底边向上翻折，其边缘恰好达到三棱锥的顶点，如图所示．设正三棱锥的底面边长为xcm，体积为Vcm3．在所有能用这种包装纸包装的正三棱锥装饰品中，V的最大值是多少？并求此时x的值．

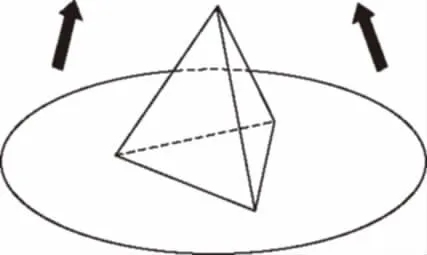
【解析】正三棱锥展开如图所示．当按照底边包装时体积最大．

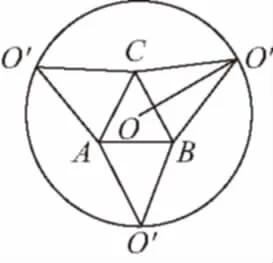
设正三棱锥侧面的高为h0，高为h．

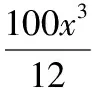
【变式1】设正四棱锥的侧棱长为1，则其体积的最大值为________．

【变式2】有一个各条棱长均为a的正四棱锥，现用一张正方形包装纸将其完全包住，不能剪裁，但可以折叠，则包装纸的最小边长是________．

【变式3】如图，圆形纸片的圆心为O，半径为5 cm，该纸片上的等边三角形ABC的中心为O.D，E，F为圆O上的点，△DBC，△ECA，△FAB分别是以BC，CA，AB为底边的等腰三角形.沿虚线剪开后，分别以BC，CA，AB为折痕折起△DBC，△ECA，△FAB，使得D，E，F重合，得到三棱锥.当△ABC的边长变化时，所得三棱锥体积(单位：cm3)的最大值为________.

3.5构造二次函数求最值

【典例】如图所示，为了制作一个圆柱形灯笼，先要制作4个全等的矩形骨架，总计耗用9.6米铁丝，再用S平方米塑料片制成圆柱的侧面和下底面(不安装上底面).当圆柱底面半径r取何值时，S取得最大值？并求出该最大值(结果精确到0.01平方米).

【解析】设圆柱形灯笼的母线长为l，则8l+16r=9.6，

解得l=1.2-2r(0lt;rlt;0.6)，

则S=2πrl+πr2=2πr(1.2-2r)+πr2=-3π·(r-0.4)2+0.48π，

当r=0.4时，S=0.48π≈1.51，S取得最大值约为1.51平方米.

【评注】在求表面积或体积的最值时，常常将目标表示为某个量(半径或高等)的二次函数，然后用配方法寻求最值(注意标出定义域).

【变式1】已知圆锥的底面半径为R，高为3R，在它的所有内接圆柱中，全面积的最大值是________．

【变式2】已知圆锥的底面半径为R，高为3R，在它的所有内接圆柱中，侧面积的最大值是________．

3.6构造三角函数求最值

【典例】如图，半径为R的球O中有一内接圆柱．当圆柱的侧面积最大时，球的表面积与圆柱的侧面积之差是________．

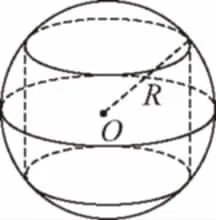
【解析】如图，设球的一条半径与圆柱相应的母线夹角为α，

则圆柱的侧面积S=2π·Rsinα·2Rcosα=2πR2sin2α，

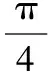
此时球的表面积与该圆柱的侧面积之差为2πR2．

【评注】在球的相关截面中，我们常常将从球心引出的角度设为参量α，将目标量表示为参量α的三角函数，然后由正弦值或余弦值的有界性[-1,1]，得出目标函数的最值.

【变式1】点P在直径为2的球面上，过P作两两垂直的三条弦，若其中一条弦长是另一条弦长的2倍，则这三条弦长之和为最大值是________．

【变式2】如图所示，三棱锥P-ABC的底面ABC为等腰三角形，AB=AC=a，侧棱长均为2a，问BC为何值时，三棱锥P-ABC的体积V最大，最大值是多少？

参考答案

1 公式法求几何体的体积和表面积

1.1几何体的侧面积与表面积

【典例1】1.6π 【解析】底面圆的周长2πr=2π，所以圆柱的底面半径r=1，所以圆柱的侧面积为4π，两个底面积为2πr2=2π，所以圆柱的表面积为6π.

2.A 【解析】以正方形的一边所在直线为轴旋转得到的圆柱底面半径r=1，高h=1，所以侧面积S=2πrh=2π.故选A.

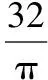
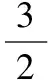
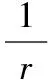
3.2 【解析】将该长方体站立放置，分别是直三棱柱、直四棱柱、直三棱柱．VAA1G-DHD1=VA1GBM-D1HCN=VMBB1-NCC1,由于它们等高，因此底面积也应该相等，也就是说SRt△A1AG=S=SRt△BB1M，即AG×h=GB×h，所以AG=2GB．所以=2.

1.2“选准底面，找对高”

【典例】

1.【解析】(1)4个面围成几何体是一个三棱锥，它的底面是AEF，B,C,D三点重合于一点，设为点H，侧棱AH，HE，HF两两垂直，如图1.

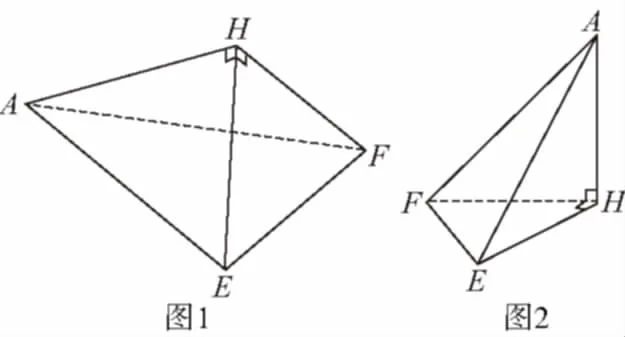
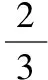
1.3认清几何体中的相关元素

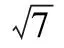
1.4用直截面法求几何体的体积

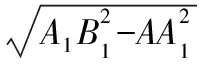
1.5用等体积法求体积

【典例1】

3.【解析】(1)证明：由勾股定理知，

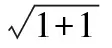
则A1A2=A1E2+AE2，

所以A1E⊥AE.

因为AD⊥平面AA1B1B，A1E⊂平面AA1B1B，

所以A1E⊥AD，

而AD∩AE=A，所以A1E⊥平面ADE.

【典例2】

1.D 【解析】连接BD，AC，因为AC⊥BD,AC⊥DD1,BD∩DD1=D,则AC⊥平面BB1D1D，BE⊂平面BB1D1D，所以AC⊥BE,A正确；BD∥B1D1，EF∥平面ABCD正确；又因为△BEF面积是定值，AC⊥平面BB1D1D，三棱锥A-BEF的高即为A到平面BB1D1D的距离，所以三棱锥A-BEF的体积是定值，从而A，B，C正确.因为点A，B到直线B1D1的距离不相等，所以△AEF的面积与△BEF的面积不相等，D错误.故选D.

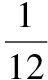
2.球的相关计算

2.1球的截面的性质

【典例1】

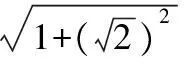
2.2将三棱锥补形成长方体求外接球的半径

2.3确定球心的位置

3简单几何体中的最值问题

3.1利用运动变化的观点求解几何体的最值

【典例1】

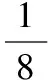
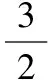
3.2利用侧面展开图“化曲为直”求距离的最值

3.3利用基本不等式求体积的最值

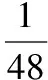
3.4利用导数求体积的最值

【典例1】

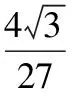
3.5构造二次函数求最值

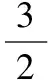
3.6构造三角函数求最值