加权N-W核估计量的渐近正态性研究

张颖

（济南大学数学科学学院，济南250022）

0 引言

在经典的计量经济学参数回归分析中，进行统计推断之前，一个最为关键的任务就是提前预设好参数模型的函数形式。通常经济数据具有较强的时变性和复杂的结构特征，难以确定其分布的具体函数形式。显然，对于同一个问题，如果设定不同的函数形式，会得到不同的参数模型，从而估计得到不同的模型参数，以及后续的统计推断也是不同的。可见提前进行的模型设定会直接决定所构建的计量经济模型能否准确地刻画所要研究的经济问题。为此出现了模型设定检验的一系列方法，Eubank(1992)[1]指出，在实际经济数据的分析中，经常会碰到“检验不一致性”的问题，即在某些方向上，参数检验方法具有较低的检验效率。

为了回避模型检验中出现的“不一致性”问题，学者们开始寻求不需要进行模型函数形式设定的建模思路，这就是非参数回归模型。非参数回归分析不需要对模型的函数形式进行预设，从而不需要进行所谓的参数估计，而是直接对目标函数进行推断，因此非参数回归模型是数据驱动型的模型，这种建模方法可以更好地适应数据的变化，从而具有拟合精度较高、可靠性强、结果更为稳健、适用范围广等优势。非参数回归模型尤其适用于那些信息获取较少的情形，比如无法用有限个参数刻画的总体分布，或者仅仅知道分布是连续的、存在密度函数等有限信息的情形。

在非参数回归模型中，最早出现的是非参数核回归方法。Nadaraya(1964)[2]和Watson(1964)[3]提出了Nadaraya-Watson(N-W)核估计，N-W核估计方法直接对抽象的回归函数m(x)=E(Y|X=x)进行估计。之后，非参数回归核估计方法获得了迅速的发展，Robinson(1983)[4]给出了非参数模型中条件均值函数的核估计量的渐近理论，此后，Collomb(1986)[5]、Masry(1995)[6]和Laïb(2000)[7]等分别基于核估计在不同条件下研究了条件均值函数的相合性、渐近正态性和收敛速度以及带宽选择的渐近最优性等问题。

局部多项式方法在非参数估计中也广为流行，因为它具有良好的数学性质、偏倚的缩减性和边缘效应的适用性，从方法实施的难易程度来看，NW估计量的实施要比局部线性估计量更为容易，并且回归函数的被估计值总是位于响应变量的范围之内。然而，相对局部线性估计量来说，NW估计量具有更大的偏倚、非适应性和边界效应。为了同时获取NW和局部线性估计量的优点，Cai(2001)[8]和De Gooiger(2003)[9]提出了加权NW估计方法。Song Y(2013)[10]提出了再加权NW估计方法，并且将其用于二阶跳扩散过程的估计中。

虽然加权NW方法很早就被提出了，但是其中的某些统计学性质并没有得到圆满的解决，为此本文在已有的加权N-W核估计量的基础上，严格证明加权N-W核估计量在给定的条件下满足渐近正态性，最后利用模拟研究检验了加权N-W核估计量的有效性。

1 非参数N-W核估计

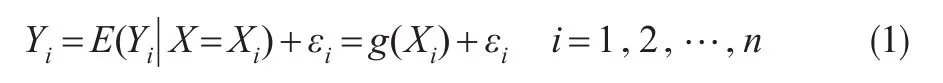
其中g(⋅)为某个未知待估的条件期望回归函数，εi为相互独立同分布的随机误差项，且满足E(εi)=0，Var(εi)=σ2＜+∞，条件期望回归函数g(x)为：

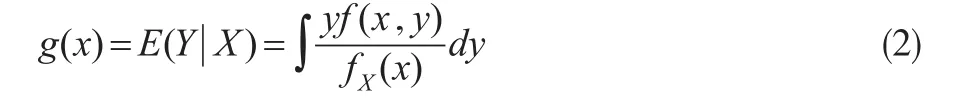
其中fX(x)为X的边缘概率密度函数。

式(2)中包含未知的联合概率密度函数f(x,y)和边缘概率密度函数fX(x)，利用非参数核密度估计法，有。其中，h0为变量Y的平滑参数，h为变量X的平滑参数，所以有

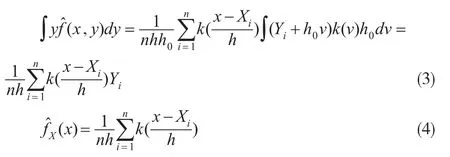
将式(3)和式(4)同时代入式(2)，就得到了g(x)的非参数回归估计：

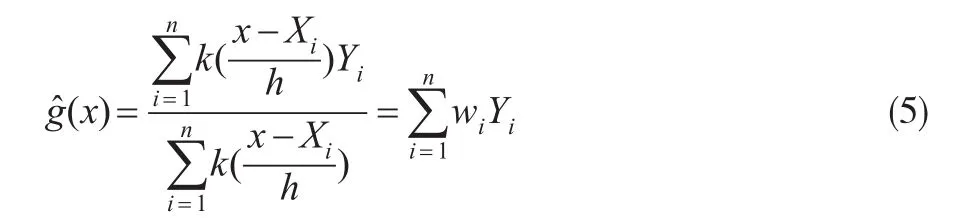
1964年和1965年美国的G.Watson与前苏联的E.Nadaraya分别在《Sankhya》和《Theory of Applied Probability》上各自独立发表了这种直接对未知函数形式的回归函数g(x)=E(Y|X)进行估计的核函数估计方法，因此式(5)被称为著名的N-W核估计量。

2 加权N-W核估计量

虽然N-W核估计是核回归估计中特别重要的一种方法，但它却存在一定的缺点。如利用N-W核估计量对边界点处的回归函数进行估计将会出现较大的偏差。为了提高回归估计的精度，减少估计偏差，需要对N-W估计量进行了局部修正，构造加权N-W估计量。

加权N-W核估计量定义为：

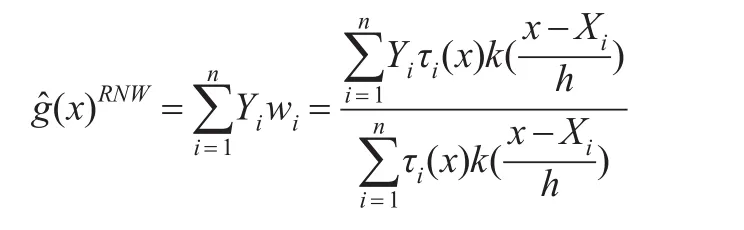
概率权函数τi(x)满足以下条件：

3 加权N-W核估计量的渐近正态性

为了证明加权N-W核估计量的渐近正态性，首先给出下面的一些基本假设条件。

条件1：核函数k(⋅)是一个对称有界的密度函数，满足∫uk(u)du=0，∫u2k(u)du＜∞。

条件2：对于固定的x，f(x)＞0，f(⋅)和σ2(⋅)在x处连续，g(⋅)在x的邻域有连续的二阶导函数。

条件3：给定X=x时，Y的条件密度函数有界。

记uj=∫ujk(u)du，νj=∫ujk2(u)du，σ2(x)=Var(Yi|Xi=x)。

在这些假设条件下，加权N-W核估计量的极限分布由下面的定理给出。

定理：在条件1至条件5成立的条件下，有：

De Gooijer(2003)[9]证明了当满足条件1、条件2、条件5时，τi(x)=φi(x)(1+op(1))，其中

令εi=Yi-g(Xi)，则：

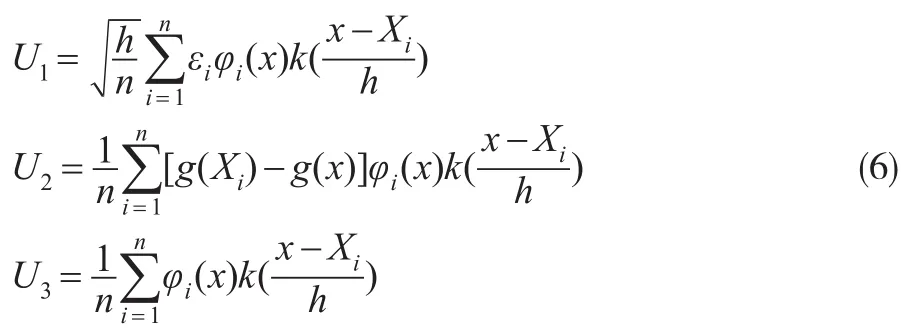
利用泰勒公式，可以得到：

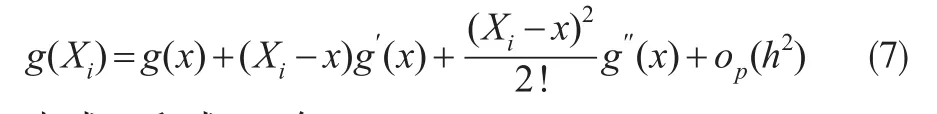
由式(6)和式(7)，有：

又因为E(εi|Xi)=0,E(Θi)=0，故E(U1)=0。

由条件3：

利用李亚普诺夫定理，对δ＞0，当n→∞时，有：

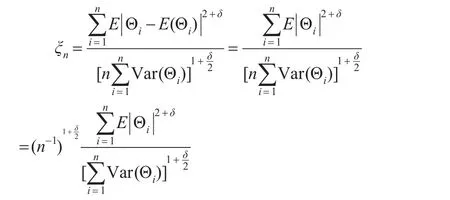
由条件4：

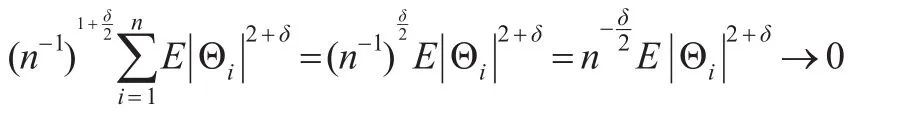
因此，ξn→0，U1的渐近正态分布性质得证。定理得证。

4 模拟

本文使用拟合优度和均方误差（MSE）来评价估计效果，其中利用R软件由以下两个模型分别模拟容量为200的两个样本，来比较加权N-W核估计量与N-W核估计量估计的精度。

模型1：Y=Xcos2πX+ε，其中ε～N(0,0.1),X～U[0,1]。

模型2：Y=sin2πX+ε，其中ε～N(0,0.1),X～U[0,1]。

计算结果见表1。

表1 加权N-W核估计和N-W核估计的拟合优度和均方误差

由表1可以看出，模型1和模型2的加权N-W核估计同N-W核估计相比较，均方误差均较小，而拟合优度都有所提高。

图1 模型1的加权N-W核估计和N-W核估计

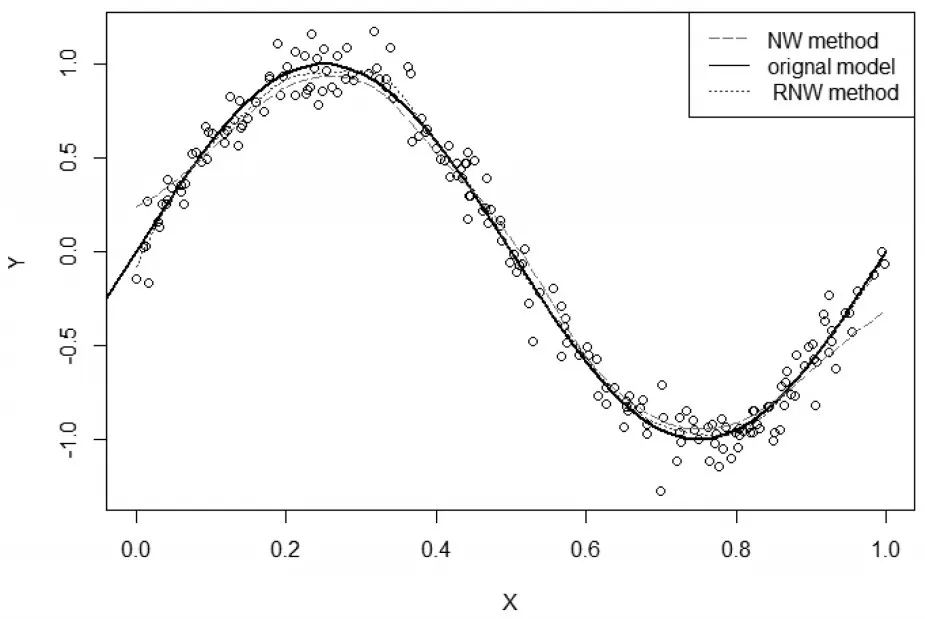
图2 模型2的加权N-W核估计和N-W核估计

由图1和图2可以看出，从整体拟合效果上观察，发现加权N-W核回归估计曲线几乎与回归曲线重合，估计效果明显优于N-W核回归估计，特别是在稀疏样本点和边界点处，表现得更为明显。通常，使用N-W核回归分析方法拟合曲线时，边界点的估计偏差较大，即存在边界效应，而用加权N-W核回归分析方法却能很好地减少边界效应。

5 结论

对于非参数核回归方法NW方法的一个实质性的改进就是加权NW方法，该方法可以用于估计独立抽样条件下的回归函数，也可以用于估计时序数据的条件分布和用于估计条件分位数。但是，对于时序数据的样本的非参数回归设定下，这些方法没有得到理论的支持。本文深入探索了加权NW方法和渐进正态性，在给定的条件下，严格证明了加权N-W核估计量的渐近正态性。证实了无论是在内点还是边界点上，加权NW都满足渐进正态性。最后，通过模拟研究进行对比性研究。模拟结果表明，利用非参数核估计法估计回归函数时，加权N-W核估计量要优于N-W核估计量。

本文虽然严格证明了加权NW方法的渐进正态性，但是限于理论方法的限制，本文没有对于加权NW方法的一致性和有效性进行证明。本文只是进行了随机模拟试验研究，而没有将该方法用于实际数据，利用该方法解决实际经济和金融中的应用问题是下一步研究的方向。

[1]Eubank R L.Applied Nonparametric Regression[J].Technometrics,1992,35(2).

[2]Nadaraya.On Estimating Regression[J].Theory Probability and Its Applications,1964,9(1).

[3]Watson G S.Smooth Regression Analysis[J].Sankhya Ser A,1964,26(4).

[4]Robinson P M.Nonparametric Estimation for Time Series[J].Journal of Time,1983,4(3).

[5]Collomb G,Härdle W.Strong Uniform Convergence Rates in Robust Nonparametric Time Series Analysis and Prediction:Kernel Regression Estimation From Dependent Observations[J].Stochastic Processes and their Applications,1986,23(1).

[6]Masry E,Tjøstheim D.Nonparametric Estimation and Identification of Nonlinear ARCH Time Series:Strong Convergence and Asymptotic Normality[J].Econometric Theory,1995,(11).

[7]Laïb N,Ould-Saïd E.A Robust Nonparametric Estimation of Autoregression Function Under Ergodic Hypothesis[J].Canadian Journal of Statistics,2000,28(4).

[8]Cai Z.Weighted Nadaraya-Watson Regression Estimation[J].Statistics and Probability Letters,2001,51(3).

[9]De Gooijer J G,Zerom D.On Conditional Density Estimation[J].Journal of Statistical Planning&Inference,2003,57(2).

[10]Song Y,Lin Z,Wang H.Re-weighted Nadaraya-Watson Estimation of Second-order Jump-diffusion Model[J].Journal of Statistical Planning&Inference,2013,143(4).