对称群及帮派论

李科

摘 要：文章首先从使数轴具有对称性的负数开始，再从距离入手找出了使整数和奇数具有对称性的法则，进而引出素数对称群Li（yP）概念，依据Li（yP）的性质将所有素数对称群的集合称为帮B（P）——一个全新的数学模型，续而结合哥德巴赫猜想探讨帮的性质，即发现帮的素数DNA的遗传性和帮的派函数Pi（i）。

关键词：对称群；数论；素数；帮派论；帮；DNA

中图分类号：O156

文献标识码：A

在《对称群与哥德巴赫猜想》一文中为了解决哥氏猜想（1+1）证明的问题引入了一个新的群——“整数的对称群”。但由于篇幅及目的等问题没能就其深刻含义进行进一步的探究，果不其然，刚发表就有读者表示看不大明白。这是很正常的，毕竟新的数学模型（新分支对称群的集合-帮论）被接受是需要适应期的。所以我认为有必要对这个我在高温假期间创建于海边的理论做单独且较为科普式的讲解。不多说，详见下文。

一、对称群及帮的概念

1.对称群的由来

我们知道，全体实数可以用一条数轴表示，那么全体整数自然也可用该数轴表示。具体地说，整数可以用数轴上一连串的点表示，如图1所示。

图1中，可以看出当人们引入负数后0成了数轴的中心，所有自然数有了关于0点的对称点-负数（用本文的观点也称为0的整数对称群）。关于0点对称的整数有无穷多个。但整数关于1对称吗？关于2对称吗？也就是说为何1和2等整数不能作为对称中心（对称轴）呢？

当然可以，只是不能在以整数元素自身作为性质判断了。如果将整数到对称中心的距离作为考察性质，群自然出现了，问题迎刃而解（且不影响0）。比如，1的整数对称群的元素为（1，1）（0，2）（-1，3）（-2，4）等，对称距离分别为0，1，2，3...；3的整数对称群有（2，4）等。它们的元素对依旧是无穷多个（无穷群）。而3的素数对称群元素只有（3，3）；4的素数对称群元素只有（3，5）；5的素数对称群只有元素（5，5）和（3，7）；越往后对称群的元素组可能越大，但由于最小的奇素数为3，最小对称轴为3，所以只有正无穷的素数对称群才会拥有无穷多个元素（对）。这样的群的元素往往是有限的（有限群）。至此我们对“对称群”有了初步的了解。

2.对称群概念

笔者在《对称群与哥德巴赫猜想》中对于对称群的定义为：凡是某数集X中存在元素x关于特定数y存在对称数 τ（x）且τ（x）也属于数集X，则称其为y的某数集对称群，记做Li（yX）。其中Li表示对称群，y为特定数（对称轴），X表示某数集。如整数对称群Li（yN+）的x和τ（x）都是整数，奇数对称群Li（yO+）的x和τ（x）都是奇数，（奇）素数对称群Li（yP）的x和τ（x）都是素数（这些群的計算不是加或乘，而是180°旋转，其逆为反旋转）。关于整数、奇数和素数的对称群举例参见表1：

从表1中可以看出，所有Li（yP）?Li（yO+）? Li（yN+）。虽然该表述可以表达意思，但是却显得不够清晰，因为将一个具有对称性质的群的集合只称为集合有欠妥当。正如第1小点中所述，所以关于整数、奇数及素数的对称群也可简单定义为关于固定数y对称的同属性数集。该数集若是整数就称为数y的整数对称群，以此类推，具体到整数、奇数、素数举例如下：

（1）1的整数对称群Li（1N+）=（1，1）（0，2）（-1，3）（-2，4）等无穷多元素；

（2）4的（正）奇数对称群Li（4O+）=（3，5）（1，7）；

（3）4的素数对称群Li（4P）=（3，5）。

若将这些群用对称轴及元素到对称轴距离的图形表示会更具形象化，在此列举几例，参见图2：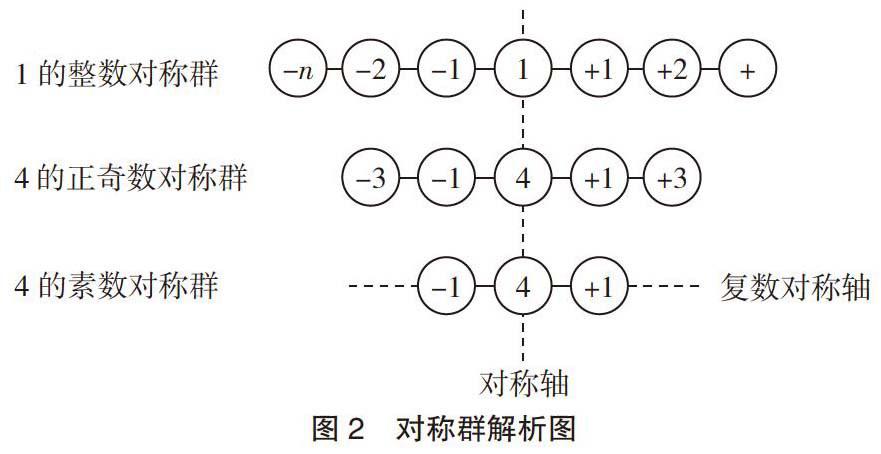

从图2中可明显看出，特定数y的各种属性的对称群，如同一枚枚晶体悬挂在数轴上。至此我们可以说：负数的引入使得数关于0对称了；复数的引入使得数关于数轴对称了；对称群的引入使得数关于数对称了（可谓第三次数轴革命，在实数轴上对称群只有一个对称轴，如果引入复数，那将是另一片天地，在此不赘述）。

3.帮-对称群的集合

无论哪种群，若群的对称轴也具有某一共同性质，我们将所有对称轴对应的群集合成为“帮”，记做BY（X），读作Y的X对称帮。其中B表示帮，X为某数集性质，Y为对称轴集合（为整数时省略）。所以帮实际是所有具有同一性质群的集合。所以关于所有整数的整数对称群称为整数的整数对称帮（简称整数的整数帮）；所有整数的奇数对称群称为整数的奇数对称帮；所有整数的素数对称群称为整数的素数对称帮；当然所有对称轴为偶数的整数对称群称为偶数的整数对称帮。这种表述更为妥当，所以《对称群与哥德巴赫猜想》找到了所有整数的素数对称群实为证明了整数的素数对称帮的存在定理。那么有关这个对称群集合“帮”的研究就可以简称为“帮论”了。《对称群与哥德巴赫猜想》由于侧重点原因而没有细说有关帮（整数的素数帮）的性质，以下就几条重点的加以介绍，以便于更好地理解这一全新概念。

二、整数的素数帮的性质

（一）帮的元素

由于只有素数2为偶数，所以文中整数的素数帮指的是整数的奇素数帮。既然帮是具有同一性质对称轴的对称群的集合，那么帮的元素自然就是所有对称群，对称群的元素才是具体的数集。有关帮及对称群元素的性质，可以将帮分类：

若每个对称群的元素等同于所有对称群的元素，这个帮就称为大帮，如整数的整数帮是大帮；若对称群的元素少于所有对称群的元素，这个帮就称为小帮，如整数的素数帮是小帮。

若帮的对称轴增加其对应的对称群元素组也增加的帮称为递增帮（整数的正奇数帮）；反之称为递减帮。

若帮中的对称群的对称轴是沿数轴两个方向的成为双向帮（整数的整数帮）；而只沿单方向的成为单向帮（整数的素数帮）。

总之，有关帮及元素等不同性质的变化可讨论帮的各种特性，可根据具体需要进行探讨，此处不赘述。

（二）素数帮

从绪论看到现在，对于对称群及帮的概念也许有了进一步的了解。但也可能有点转向，为便于深刻理解整数的素数帮，请看图3：

从图3中可以清楚地看出什么是对称轴，什么是素数对称群及其与帮的关系。请认真区分，下面将借此讲述素数对称帮的性质。

1.素数帮的性质

这点似乎毋庸置疑，但由于据此可以巧证哥德巴赫猜想而不得不提及。其存在性主要是因为素数的对称数无法由已知素数（对称轴前素数）因子乘积表示，参见表2（证明参见文献[1]）。

从表2中可明显看出最小素因子乘积（奇合数）大于对应的2m，且其增大速度远大于2m的增大速度（如3*3仅仅大于2*4，而3*7已经大于2*10），如此必然致使已知素数因子乘积无法按律表示足够多的对称数，不能按律用素数因子乘积表示的即为素数，只有存在素数才能使对称数完整，即整数的素数帮B（P）存在。由整数的素数帮B（P）的存在可得B（P）中的任一对称群Li（yP）的对称轴两倍，可用两个素数元素p及τ（p）加和表示，而所有整数（对称轴）的两倍就是全体偶数，所以Like-Gold设想成立（有关具体证明参见文献[1]）。但其中涉及所谓的律及“遗传性”有必要在此用几句话再说清楚点，不然当对称数足够大时m到2m间的奇合数在不按律的情况下是可以填满对称数位置的。所以整数的素数帮中群的遗传性也是十分重要的且更为直观的理解。我借助计算机找出30以内整数的素数对称数，参见表3：

显而易见，表3中可以看出很多关于对称数的规律，比如：①对称数第1列全部为新数（基因突变），且就是整个奇数集（对称轴的两倍-最小奇素数3）；②当对称轴到素数时增加一列，且此列为以该素数开头的奇数集合（相同奇数相对于第一列下移了（列最小素数P-最小奇素数3）/2个单位）；③所有的对称数都遗传自对称轴小于自己的群（表3中选取了部分用斜线链接，每个素数被遗传的次数等于以该素数为对称轴的对称数列数），等等。这其中就包括所有的素数，所以当从中筛选出整数的素数帮时可以说素数是整数的素数帮中群的DNA（就如同把素数比作合数的原子）。DNA只能遗传，我们可以说下一个群中必有已经出现过的素数基因，但它又可能不同于其他已出现的群（遗传中伴有突变），这和DNA的性质完全一致，所以把素数比作帮中群的DNA很是恰当。所以也可以理解帮为具有同样遗传性质的群。

帮中群之所以具有遗传性，是因为已知素数的整数对称数必须跟已知素数对应这一根本性质决定的（比如3，5，7是连续的奇数使得表3中前3列为连续的奇数；后续的对称数也都必须按DNA规律遗传前面的群；等等）；而群遗传的规律性则是由于已有素数的位置固定而决定的（对称数=行最大奇数O-列最小素数P+最小奇素数3；由伯特兰·切比雪夫定理可知表3中大括号内必有素数；首列两相连素数间合数的个数小于小素数行最右端数到大素数行最左端数之间素数的个数），该规律致使整数前素数关于其的对称数都具有素數（从几何的角度看即为素数的整数对称数集合的行封闭性），即整数的素数帮存在（对称轴6及以后都有合数，且也可轻易看出1+2的成立等）。

2.B（P）中Li（yP）的距离函数Ke（N）

从Li（yP）的定义可以看出，Li（yP）的元素可能不只一对素数。但肯定有一对距离对称轴N最近的一对素数，我们将这对素数到N的距离定义为距离函数，用符号Ke（N）表示。由此可得到一系列性质，如Ke（N）=0时所有解为素数，Ke（N）=1的所有解±1就是孪生素数对（感兴趣者可深入研究，不过奇异映射Ke（N）是很矫情的，不易俘获）。

3.B（P）中的派系函数Pi（i）

任何的帮中都可能出现不同的派系，整数的素数帮自然也不例外。为便于从错综复杂的帮中揪出派系，我们将表2中群的τ（p）按照正常升序单独列出并标记各群中元素对的个数（τ（p）的个数），参见表4。

从表4中可以看出表3在找遗传性中的优势（如果只看出其然而不明其所以然，参见下节），此外可以轻松地看出B（P）中各Li（yP）的p与τ（p）的对数（个数）随着对称轴的增加而起伏上升，所以在帮论中哥德巴赫猜想显然成立（且不小于14的偶数可能都至少有两组1+1形式）。为易于察觉，以对称轴为横坐标，各个群中元素τ（p）的个数为纵坐标作图，参见图4：

从图4中可以更加明显地看出B（P）中各Li（yP）的p与τ（p）的对数（个数）随着对称轴的递增而起伏上升，且振幅越来越大（似乎某段有上下限）。此外还隐约看出τ（p）的个数在不规律的同时似乎又像台阶一样逐渐抬升（形成了不同的阶层），比如：

第一阶层：[1，2]，群个数为4（3，4，5，6的素数群，横坐标）；

第二阶层：[2，n]，群个数为m（横坐标7至6+m）；

第三阶层：[3，o]，群个数为q（横坐标7+m至6+m+q）；

……

我们把这样的阶层称之为“派”（也有“派生出来”之意），符号为Pi（i）。i表示第i派系（τ（p）个数的下限），在数值上等于Li（P）中所有距离值（正整数）；Pi（i）即为第i派中群的个数，如第1派Pi（1）=4。那么派的个数是无穷多的吗（又或许当对称轴达到某个整数后τ（p）的个数永远都会回到某值）？这个猜想在此不赘述，留给大家作为习题思考（Li（34P）的元素为2对，若只有两个派系其只有两对元素的群对称轴有何规律呢？）。

至此，大家应该明白，整数的素数对称群集合或帮的存在说明哥德巴赫猜想成立；而派猜想的成立将说明第1派中的偶数（对称轴乘2）至少有一对1+1，第2派中至少有两对1+1，第3派中将至少有3对1+1，等等。所以哥猜想的成立在派函数中是显而易见的。有关“帮派论”就讲述到此，至于其他运用期待广大数学家挖掘（比如所有有理等边三角形是否是密铺整个平面的一个帮）。

4.Li（yP）与Li（yO+）关系

为进一步理解表2的重要性或其由来，可参见表5“整数的素数群与整数的奇数群关系”：

从表5中可以看出，所谓偶数就是群对称轴的偶素数倍；它能否由两个素数加和表示取决于C群的存在性；表中A群就是整数的奇数对称群Li（yO+），C群就是所述的整数的奇数对称群Li（yP），而B群就是两者之间的过度对称群（其元素对为素数和奇数）；若能证明过度群B中的奇数必有素数就可说明群C是存在的（C群?B群?A群）。群B的所有对称数不就是与已知素数关于整数的对称数吗？这不正是表2吗？

三、总结

本文首先从发现使数轴具有对称性的负数开始，再从距离入手找出了使整数和奇数具有对称性的法则；使读者思维逐步开阔，进而引出整数的素数对称群Li（yP）概念；依据Li（yP）的性质将所有素数对称群的集合称为帮B（P）；续而结合哥德巴赫猜想探讨帮的性质，即发现帮的素数DNA的遗传性和帮的派函数Pi（i）。

参考文献：

[1]李 科.对称群与哥德巴赫猜想[J].读写算（教师版），2017（21）：3-5.

[2]饶世麟.关于对称群特征的计算问题[J].装备学院学报，2000，1（3）.

[3]饶世麟.对称函数与对称群特征标[J].指挥技术学院学报，1996（1）.

[4]刘雪成.对称群自旋表示的特征标[J].自然杂志，1989（3）：239-240.

[5]陳松良.对称群S5和交错群A5的复特征标表[J].陕西教育学院学报，2003（1）：73-75.

[6]唐有琪.对称性原理（二）：有限对称群的表象及其群论原理[M].北京：科学出版社，1977.

[7]张冬波.几何中的偏微分方程及其对称群[D].西安：西北大学，2006.

[8]康 静，王丽真.方程组基本解的对称群方法[J].西北大学学报（自然科学版），2011（6）：941-945.

[9]朝 鲁，张鸿庆，唐立民.一个计算微分方程（组）对称群的Mathematica程序包及其应用[J].计算物理，1997（3）：5.

[10]熊廷煌.对称群浅论[J].荆州师专学报，1978（0）：32-45.

[11]范久瑜.对称群的Kazhdan-Lusztig R-多项式的计算[D].天津：南开大学，2012.

[12]屠伯埙.对称群的特征标与一个行列式问题[J].复旦学报（自然科学版），1994（4）：8.

[13]冯培恩，马友才，邱清盈，等.机械零件对称群及其在面向装配设计中的应用[J].机械工程学报，2013（11）：98-105.

[14]郑雨军，丁世良.动力学对称群方法对三原子分子高激发振动态的理论研究[J].物理学报，1999（3）：8.